|
|
Premier principe de la thermodynamique et bilan énergétique Exercices |
|
|
|
|
|
QCM r
|
1)- Exercice 05 page 312 : Déterminer un volume molaire :
|
Déterminer un volume molaire : 1. Exprimer le volume molaire Vm
d’un gaz parfait en fonction des données littérales de l’équation
d’état. 2. Calculer le volume molaire Vm
d’un gaz parfait : a. Dans les conditions normales de température et de pression : Ta = 273 K et Pa
= 1,013 × 105 Pa ; b. Dans les conditions standard de température et de pression : Tb = 298 K et Pb
= 1,00 × 105 Pa
-
Données :
-
Équation d’état du gaz parfait :
P . V
= n . R . T
-
Constante
des gaz parfaits : R = 8,314 Pa . m3 .mol–1 .
K–1 |
|
Déterminer un volume molaire : 1.
Volume molaire Vm d’un gaz
parfait.
-
Équation d’état du gaz parfait :
-
Cette équation relie les
différentes grandeurs macroscopiques qui permettent de le décrire.
-
Volume du gaz parfait :
-
-
Expression du volume molaire du gaz
parfait :
-
C’est le volume d’une mole de gaz :
n = 1
-
2.
Calcul du volume molaire Vm
d’un gaz parfait : a.
Valeur dans les CNTP :
-
Ta = 273 K et
Pa = 1,013 ×
105 Pa ;
-
b.
Valeur dans les CSTP :
-
Tb = 298 K et
Pb = 1,00 × 105
Pa ;
-
-
La valeur du volume molaire d’un gaz
est très sensible à celles de la température T et de la Pression
P. |
||||||||||||
2)- Exercice 07 page 312 : Exprimer une masse volumique :
|
Exprimer une masse volumique : 1.
Masse volumique ρ, quantité de
matière n et masse molaire M. a. Rappeler l’expression de la masse volumique
ρ d’un corps, puis l’exprimer en faisant apparaître la
quantité de matière n et la masse molaire M. b. Donner l’expression de la quantité de
matière n d’un gaz parfait en fonction des données littérale
de l’équation d’état. 2. Exprimer la masse volumique ρ d’un
gaz parfait en fonction de sa masse molaire M et des grandeurs de la
question 1. b. 3. L’expression de la question
1. b
est-elle toujours valide si la pression devient très grande ?
-
Données :
-
Équation d’état du gaz parfait :
P . V
= n . R . T |
|
Exprimer une masse volumique : 1.
Masse volumique ρ, quantité de
matière n et masse molaire M. a.
Expression de la masse volumique ρ
d’un corps.
-
Quantité de matière :
n
-
Masse molaire :
M
-
Masse :
m = n .
M
-
Masse volumique d’une
substance gazeuse :
- b.
Expression de la quantité de matière n
d’un gaz parfait en fonction des données littérale de l’équation
d’état.
-
Équation d’état du gaz parfait :
-
Cette équation relie les
différentes grandeurs macroscopiques qui permettent de le décrire.
-
Quantité de matière d’un gaz
parfait :
-
2.
Expression la masse volumique ρ d’un
gaz parfait en fonction de sa masse molaire M et des
grandeurs de la question 1. b.
-
3.
Validité de l’expression de la question
1. b :
-
Dans le cas présent, on utilise le
modèle du gaz parfait.
-
Si la pression devient très grande : - Le modèle du gaz parfait n’est plus respecté (les entités du gaz sont de plus en plus proches,
la masse volumique augmente, il apparaît des
interactions entre les entités, il y a des chocs entre les entités).
-
La relation précédente n’est plus
valide. |
||||||||||||||||||||||||||||||
3)- Exercice 08 page 312 : Calculer une masse volumique :
|
Calculer une masse volumique : - La masse volumique de l’air assimilé à un gaz parfait dans les conditions normales de température et de pression est : 1,293 g . L–1.(CNTP : T1 = 273 K et P1 = 1,013 × 105 Pa) - Calculer la masse volumique de l’air dans les conditions standard de température et de pression (CSTP :
T2 = 298 K et
P2 = 1,000 ×
105 Pa).
-
Données :
-
Équation d’état du gaz parfait :
P . V
= n . R . T
-
Constante des gaz parfaits : R
= 8,314 Pa . m3 .mol–1 . K–1 - "Masse molaire de l'air" : M = 28,965 g . mol–1 C'est la masse de 22,4 L d'air dans les conditions normales de température et de pression. |
Calculer une masse volumique :
-
Masse volumique de l’air dans les
conditions standard
de température et de pression
(CSTP :
T2 = 298 K et P2
= 1,000 × 105 Pa).
-
À cette température et à cette
pression, on peut encore assimiler l’air à un gaz parfait :
ρ
Masse volumique d’une substance (kg . m–3 )
m
Masse de la substance en kilogramme (kg)
V
Volume de la substance en mètre cube (m3)
►
Première
méthode :
-
Dans les CNTP :
ρair = 1,293 g . L–1
-
L’air est un mélange de gaz,
principalement du diazote et du dioxygène.
-
D’équation d’état du gaz parfait, on
déterminer la relation donnant la « quantité de matière »
n d’air dans les CNTP :
-
-
Dans les conditions standard, on peut
écrire :
-
-
On peut en déduire la relation suivante après
simpification :
-
-
De cette expression, on tire la
relation qui donne le volume
V2 de la même masse
m d’air dans les
conditions standard :
-
-
Dans les
CNTP : m
Masse
d’air
m
= 1,293 g
V1
Volume d’air
V1
= 1,293 L
T1
Température de l’air
T1
= 273
K
P1
Pression de l’air
P1
=
1,013
× 105 Pa
ρ1
ρ1
=
1,293
g . L–1
-
Dans les
CSTP : m
Masse
d’air
m
= 1,293 g
V2
Volume d’air
T2
Température de l’air
T2
= 298
K
P2
Pression de l’air
P2
=
1,000
× 105 Pa
ρ2
ρ2
= ?
g . L–1
-
On peut calculer la valeur de
V2 :
-
-
Puis, on calcule la valeur de la
masse volumique
ρ2
de l’air dans ces conditions :
-
-
Application numérique :
-
-
Tableau de valeurs : m
Masse
d’air
m
= 1,293 g
V2
Volume d’air
V2
≈ 1,12
L
T2
Température de l’air
T2
= 298
K
P2
Pression de l’air
P2
=
1,000
× 105 Pa
ρ2
ρ2
≈ 1,17 g .
L–1
►
Deuxième
méthode :
-
On considère que l’air est un gaz
parfait :
-
La masse molaire de l’air :
M =
28,965 g . mol–1
-
La masse volumique ρ d’un gaz
parfait en fonction
de sa masse molaire M :
-
-
Application numérique :
-
►
Troisième
méthode :
-
On peut trouver une relation donnant
la masse volumique de l’air en fonction de
T,
P et
ρ1 :
-
Dans les CNTP :
-
Dans les CSTP
-
-
Application numérique :
-
![]()
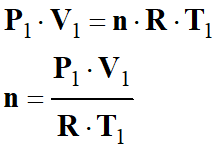
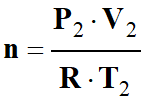
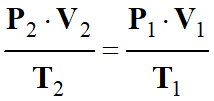
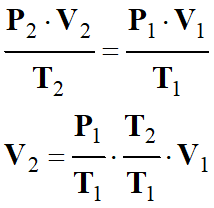
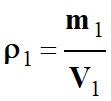
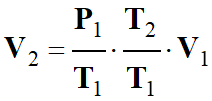
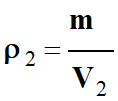
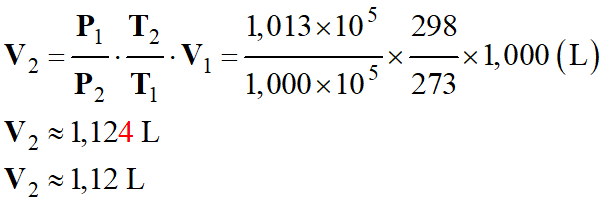
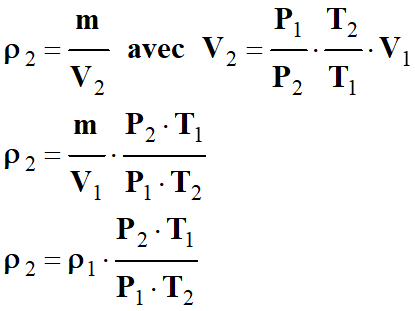
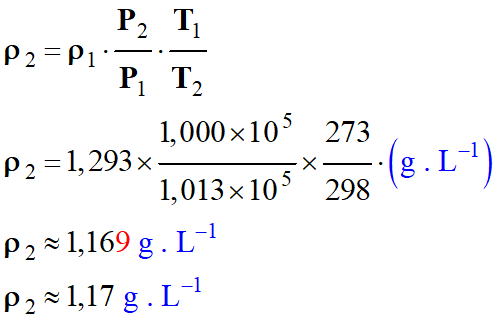
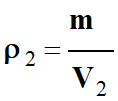
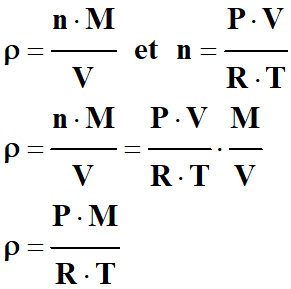
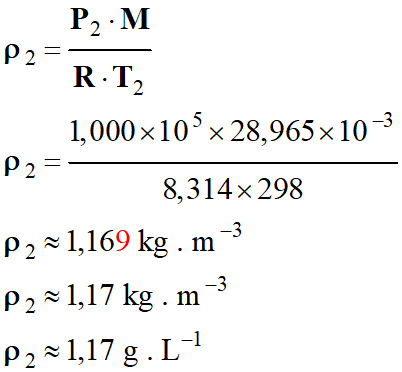
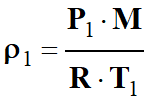

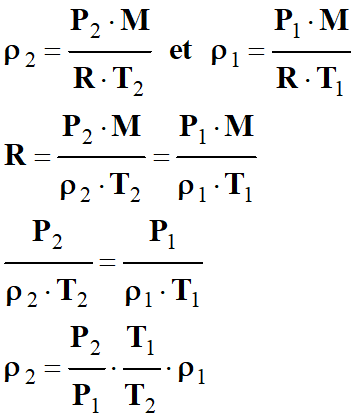
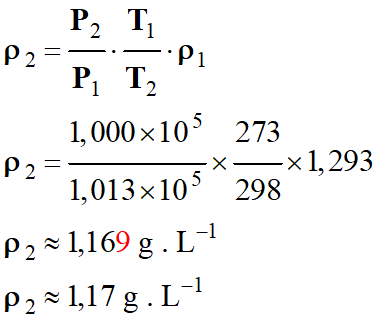
![]()
4)- Exercice 09 page 313 : Définir l’énergie interne :
|
Définir l’énergie interne : On étudie l’échauffement d’une plaquette de frein lors d’un
freinage. 1.
Proposer un système d’étude et identifier
alors le milieu extérieur. 2.
Définir l’énergie interne. |
Définir l’énergie interne : 1.
Système d’étude :
-
S = {plaquette de frein}
-
Les plaquettes de frein sont
composées de deux principaux éléments :
-
un socle en acier ;
-
et d’un matériau de friction : la
garniture.
-
La garniture (élément d’usure) est
composée de plusieurs éléments organiques ou métallique qui doivent supporter de hautes
températures.
-
Exemples : cuivre, graphite,
particules céramiques, fer, et bronze.
-
Le milieu extérieur : tout ce qui ne
fait pas partie du système.
-
ME = {disque, support,
étrier, air, …} 2.
Définition de l’énergie interne.
-
L’énergie interne est la
somme des énergies cinétique et potentielle microscopiques,
c’est
l'énergie liée à sa structure interne microscopique des entités qui
constituent la garniture,
-
L’énergie interne est
notée : U.
-
Unité : joule
(J)

![]()
5)- Exercice 11 page 313 : Connaître l’énergie microscopique :
|
Connaître l’énergie microscopique : De l’eau est maintenue à ébullition dans une casserole.
-
Relier le début et la fin des phrases
|
||||||||||||||||
|
Connaître l’énergie microscopique :
-
Énergie potentielle
microscopique :
-
Au niveau microscopique, à
toute liaison entre deux particules du système est associée une
énergie potentielle microscopique.
-
L’énergie potentielle
microscopique est due aux interactions gravitationnelle, électromagnétique, forte et faible entre les particules qui
constituent le système.
-
On distingue les énergies
potentielles microscopiques chimique, électrique, magnétique et
nucléaire.
-
Les énergies potentielles résultent
de l’énergie de liaisons chimiques et de l’énergie de masse des
noyaux.
-
On peut citer d’autres formes
d’énergies potentielles microscopiques qui résultent de liaisons
intermoléculaires entre les molécules qui constituent le système
étudié.
-
Ces énergies potentielles
microscopiques varient lors d’un changement d’état de la matière : fusion, liquéfaction, solidification.
-
L’énergie cinétique
microscopique :
-
À l'échelle microscopique,
les particules constituant le système sont animées de mouvements
individuels.
-
Cette agitation augmente
avec la température, on l'appelle l'agitation thermique.
-
C’est l’énergie cinétique
microscopique.
-
Plus la température d’un
système est élevée, plus l’agitation thermique des particules qui le
constituent est grande et plus son énergie cinétique microscopique est grande.
-
Dans le cas présent : «De l’eau est
maintenue à ébullition dans une casserole».
-
Il se produit un changement d’état
physique.
-
De l’eau à l’état liquide passe à
l’état gazeux.
-
Au cours du changement d’état, la
température du système (eau de la casserole) garde la même valeur.
-
C’est la température d’ébullition de
l’eau : T = 100 ° C (sous
la pression atmosphérique P = 1,013 × 105 Pa)
-
Elle est constante. - En conséquence, l’énergie cinétique microscopique du système reste constante (T
= 100 ° C).
-
L’énergie potentille microscopique
est modifiée (changement d’état).
-
Elle augmente.
Diagramme d’état de l’eau :
|
||||||||||||||||
6)- Exercice 13 page 313 : Distinguer des variations d’énergie :
|
Distinguer des variations d’énergie :
À cause des
interactions avec les molécules de la haute atmosphère, elle atteint une vitesse
limite. 1.
Expliquer pourquoi l’énergie mécanique Em
de la météorite diminue. 2.
Justifier le fait que toutes les formes
d’énergie de la météorite sont modifiées.
-
Donnée :
-
Énergie potentielle de la météorite
en interaction avec la Terre :
-
-
Avec
EP = 0 J si
la distance r est entre
les deux corps est infinie. |
|
Distinguer des variations d’énergie :
-
Énergie potentielle de la météorite
en interaction avec la Terre :
-
-
Avec
EP = 0 J si la
distance r est entre les
deux corps est infinie. 1.
Évolution de l’énergie mécanique Em
de la météorite :
-
L’énergie mécanique Em
d’un système macroscopique résulte de contributions macroscopiques.
-
L’énergie mécanique
Em d’un
système est la somme de son énergie cinétique
EC et
de son énergie potentielle
EP.
-
Relation :
-
Em = EC
+ EP.
-
Unité : joule (J)
-
Dans le cas présent,
-
La météorite atteint une vitesse
limite : vlim
= constante
-
L’énergie cinétique
EC
de la météorite devient constante.
-
D’autre part, la météorite se
rapproche de la Terre, la distance r entre la Terre et la météorite
diminue.
-
Le terme augmente
-
Mais l’énergie potentielle
-
L’énergie mécanique
Em de la météorite diminue. 2.
Modification des formes d’énergie de la
météorite.
-
La météorite possède de l’énergie
mécanique macroscopique Em et cette énergie diminue.
-
Elle possède de l’énergie interne
U
-
C’est-à-dire :
-
De l’énergie cinétique
microscopique ;
-
De l’énergie potentielle
microscopique.
-
Comme la météorite s’échauffe en se
rapprochant de la Terre, son énergie cinétique microscopique
(agitation thermique) augmente.
-
Son énergie cinétique microscopique
est modifiée.
-
De plus la météorite fond
partiellement lorsqu’elle se rapproche de la Terre.
-
Il se produit un changement d’état
physique, passage de l’état solide à l’état liquide.
-
Ceci entraîne une modification de la
structure de la météorite et donc une modification de son énergie
potentielle microscopique.
-
Son énergie potentielle microscopique
augmente. |
7)- Exercice 15 page 313 : Reconnaître le mode de transfert de l’énergie :
|
Reconnaître le mode de transfert de l’énergie : Lors d’une descente, les skis sont soumis à des forces de
frottement exercées par la piste. 1.
Le transfert d’énergie de la piste sur le
système {skis} s’effectue-t-il par travail ou par transfert
thermique ? 2.
Préciser le signe de ce transfert. |
|
Reconnaître le mode de
transfert de l’énergie : 1.
Transfert
d’énergie de la piste sur le système {skis} :
-
Travail ou
par transfert thermique ?
-
Les skis
sont soumis à des forces de frottement exercées par la piste.
-
Lors du
déplacement du skieur, les forces de frottement effectuent un
travail W.
-
Le
transfert d’énergie entre les skis et la piste s’effectue par
travail W.
-
D’autre
part, il se produit un échauffement local de la neige qui constitue
la piste.
-
Il se produit aussi un transfert thermique des skis
vers la piste. 2.
Signe de ce
transfert.
-
Le travail
des forces de frottement est résistant W < 0 J.
-
Le système
{skis} perd de l’énergie et le système {piste} gagne de l’énergie.
|
8)- Exercice 17 page 314 : Connaître le premier principe :
|
Connaître le premier principe : Le premier principe, pour un système au repos macroscopique échangeant de l’énergie mais pas de matière avec le milieu extérieur et qui
évolue d’un état initial à un état final, s’écrit : ΔUi→f
= W + Q 1.
Indiquer le nom et l’unité de chaque
grandeur. 2.
Préciser la convention qui détermine le
signe. |
Connaître le premier principe : 1.
Nom et l’unité de chaque grandeur.
ΔUi→f
= W + Q
ΔUi→f
: Variation d’énergie interne (joule : J)
W :
Travail (électrique ou mécanique)
(joule : J)
Q :
Transfert thermique (joule : J) 2.
Convention
qui détermine le signe.
►
Établissement d’un bilan
énergétique :
-
Il faut :
-
Définir le système au repos
macroscopique, l’extérieur est alors le reste de l’Univers ;
-
Écrire le premier principe de la
thermodynamique ;
-
Relever tous les transferts d’énergie
ayant lieu entre le système et le milieu extérieur
-
Repérer le sens de chaque transfert
d’énergie ;
-
Attribuer un
signe positif si l’énergie est
reçue
par le système ;
-
Attribuer un
signe négatif si l’énergie est
cédée par le système ;
-
Effectuer la somme de tous ces
transferts :
-
Si la somme est
positive, l’énergie interne du
système a
augmenté ;
-
Si la somme est
négative,
l’énergie interne du système a
diminué.
![]()
9)- Exercice 21 page 314 : Prévoir l’évolution de l’énergie interne :
|
Prévoir l’évolution de l’énergie interne : On souhaite refroidir de 5 ° C une masse m de jus de fruit
considéré comme incompressible. 1. Donner l’expression de la variation d’énergie interne ΔUi→f du système {jus de fruit} en fonction notamment de la
masse du système et de sa variation de température entre l’état initial et l’état final. 2.
Prévoir le signe de la variation d’énergie
interne de ce système. |
Prévoir l’évolution de l’énergie interne : 1.
Expression de la variation d’énergie interne
ΔUi→f du système {jus de fruit} :
-
La variation d’énergie
interne ΔUi→f
d’une masse m de substance dont la température varie
d’une
valeur initiale θi à une valeur finale θf,
sans changement d’état, est donnée par la
relation suivante :
ΔUi→f = m . c . (θf
– θi ) = m . c . Δθ
ΔU :
Variation d’énergie interne en joule (J)
m :
masse de jus de fruit en kilogramme (kg)
c :
capacité thermique massique du jus de fruit
(J.kg
– 1.° C– 1) ou (J.kg – 1. K–
1)
θf
– θi =
Δθ
: Variation de température
en
(°C) ou (K)
θi
: Température à l’état initial en
(°C) ou (K)
θf
: Température à l’état final en
(°C) ou (K) 2.
Signe de la variation d’énergie interne de
ce système.
-
On souhaite refroidir de 5 ° C une
masse m de jus de fruit considéré comme incompressible.
-
La température du système {jus de
fruit} diminue :
-
Δθ
= – 5 ° C
-
Le système {jus de fruit} perd de
l’énergie :
-
ΔUi→f < 0 J
![]()
10)- Exercice 23 page 315 : Pression d’un gaz :
|
Pression d’un gaz : Les appareils respiratoires contenant une bouteille d’air comprimé permettent aux sapeurs-pompiers de travailler dans des atmosphères toxiques lors d’un incendie. L’air contenu dans une bouteille d’air comprimé de volume V1 = 6,0 L est à la pression P1
= 300 bar et à la température T1 = 290 K. Pour simplifier l’étude, on considère que, dans ces conditions de
température et de pression, cet air peut être assimilé à un gaz parfait. 1.
Exprimer la quantité de matière n
d’air contenu dans la bouteille. 2.
On souhaite calculer le volume V2
d’air que cette bouteille peut libérer à la température T2
= 320 K et à la pression atmosphérique Patm =
1,013 × 105 Pa. a.
Exprimer la quantité de matière n de
l’air en fonction des données de la
question 2. b.
Calculer la valeur du volume V2. 3. En opération, le volume d’air inspiré par un pompier peut atteindre 90 L par minute. Quelle peut être la durée
de l’intervention ?
-
Données :
-
1 bar = 1 × 105 Pa.
-
R = 8,314 Pa . m3
.mol–1 . K–1. |
|
Pression d’un gaz : 1.
Quantité de matière n d’air contenu
dans la bouteille.
-
On considère que, dans ces conditions
de température et de pression, l’air peut être assimilé à un gaz parfait.
-
On peut utiliser l’équation d’état
des gaz parfaits :
-
Cette équation relie les
différentes grandeurs macroscopiques qui permettent de le décrire.
- Relation donnant la quantité de matière d'air contenu dans la bouteille : -
-
Application numérique :
-
2.
Volume V2 d’air que cette
bouteille peut libérer la bouteille :
-
La température
T2 = 320 K
-
La pression atmosphérique
Patm = 1,013 × 105 Pa. a.
Quantité de matière n de l’air en
fonction des données de la question 2.
-
On utilise l’équation d’état des gaz
parfaits :
-
b.
Valeur du volume V2.
-
-
Application numérique :
-
3.
Durée de l’intervention :
-
En opération, le volume d’air inspiré
par un pompier peut atteindre 90 L par minute.
-
On connait le débit volumique de
l’air :
-
DV = 90 L .
min–1
-
|
||||||||||||
11)- Exercice 26 page 316 : Il y a film et film :
|
Il y a film et film :
Une alternative aux films plastiques alimentaires est le film à
la cire d’abeille. Une couche fine de cire d’abeille, d’huile de jojoba et de résine
de pin est déposée sur un tissu en coton biologique. Chaque film est lavable et réutilisable environ 120 fois. Pour fabriquer la couche de cire, on utilise une cuve en
aluminium de masse m0 = 0,250 kg, chauffée par un conducteur
ohmique. La puissance électrique
Pelec de l’appareil est 200 W. La cuve contient m1 = 100 g de cire solide. L’ensemble est initialement à la température ambiante θa
= 19 ° C. 1.
Cire et échanges d’énergie : a.
Calculer la variation d’énergie interne
ΔU1 du système {cuve et cire} nécessaire pour atteindre la
température de fusion de la cire. b.
Quelles formes d’énergie de la cire sont
modifiées lors du chauffage ? 2.
Premier principe : a.
Rappeler le premier principe pour le système
et en déduire le transfert thermique Q1 à apporter au système par
l’appareil pour atteindre la température de fusion. b.
Indiquer le signe de Q1. c.
Calculer la durée Δt1 de
chauffage nécessaire pour réaliser ce transfert thermique. 3.
Il faut attendre une durée de Δt2
= 6,0 min pour que la cire fonde totalement. Calculer le transfert thermique
Q2 correspondant. 4.
En déduire le transfert thermique Qtot
nécessaire à la fusion de 100 g de cette cire.
-
Données :
-
Température de fusion de la cire :
θf = 64 ° C
-
Capacités thermiques massiques :
-
De l’aluminium :
cAl(s) = 897
J . kg–1 . °C–1
-
De la cire :
ccire = 3,4 ×
103 J . kg–1 . °C–1 |
|
Il y a film et film :
1.
Cire et échanges d’énergie : a.
Calcul de la variation d’énergie interne
ΔU1 du système {cuve et cire} :
-
Système d’étude : {cuve et cire}
-
Il est incompressible.
-
Il est constitué :
-
Cuve en aluminium de masse :
m0
= 0,250 kg,
-
La cuve contient de la cire solide :
m1 = 100 g.
-
Température initiale du système :
θi = θa = 19 ° C
-
Température finale du système :
θf =
θf = 64 ° C
-
Transfert par chaleur produisant une
élévation de température (sans changement d’état) : - La variation d’énergie interne ΔU d’une masse m de substance dont la température varie d’une valeur initiale θi à une valeur finale θf, sans changement d’état,
est donnée par la relation suivante :
-
Dans le cas présent, le système est
constitué d’une cuve en aluminium et de cire d’abeille :
-
ΔU1 = m0
. cAl(s)
. (θf – θa) + m1
. ccire
. (θf – θa)
-
ΔU1 = (m0
. cAl(s)
+ m1
. ccire
) . (θf – θa)
-
ΔU1 = (0,250
× 897 + 0,100 × 3,4 × 103) .
(64 – 19)
-
ΔU1 ≈ 2,53 × 104 J
-
ΔU1 ≈ 2,5
× 104 J b.
Formes d’énergie de la cire modifiées lors
du chauffage :
-
La température du système augmente :
-
La température de la cire augmente.
-
L’agitation thermique des entités
chimiques qui constituent la cire augmente.
-
L’énergie cinétique microscopique des
entités chimiques qui constituent la cire augmente.
-
On chauffe la cire, mais elle ne fond
pas. Il n’y a pas de changement d’état physique.
-
L’énergie potentielle microscopique
de la cire ne varie pas. 2.
Premier principe : a.
Énoncé du premier principe pour le système.
-
Énoncé :
-
La variation ΔUi→f
d’énergie
interne d’un système,
-
Qui n’échange pas de matière
avec le milieu extérieur,
-
Au repos macroscopique,
-
Qui évolue d’un état initial
(i) à un état final (f)
-
Est égale à la somme des
énergies échangées par le système avec le milieu extérieur,
-
Par travail
W
et / ou par transfert thermique
Q :
-
Dans le cas présent,
-
Le système d’étude : {cuve et cire}
-
La somme des énergies
échangées par le système avec le milieu extérieur :
-
Le système reçoit de l’énergie du
milieu extérieur grâce au conducteur ohmique sous forme de transfert
thermique.
-
Transfert thermique :
Q1
-
Il ne reçoit pas de transfert
d’énergie par travail : W = 0 J.
-
Enfin, on néglige les transferts
thermiques entre l’air ambiant et le système {cuve et cire}.
-
On peut écrire :
-
ΔUa→f =
Q1 b.
Signe de Q1.
-
Le milieu extérieur cède de l’énergie
par transfert thermique au système {cuve et cire}
-
Le système {cuve et cire} gagne
l’énergie Q1
-
Q1 > 0 J c.
Calcul de la durée Δt1 de
chauffage nécessaire pour réaliser ce transfert thermique.
-
Le transfert thermique
Q1 provient de l’énergie reçue par travail électrique par
l’intermédiaire du conducteur ohmique.
-
Il fournit l’énergie électrique :
-
Welec =
Pelec .
Δt1
-
Il en découle que :
-
Welec =
Pelec .
Δt1 =
Q1
-
On en déduit l’expression suivante :
-
3.
Transfert thermique Q2
correspondant.
-
Durée de
Δt2 = 6,0 min
pour que la cire fonde totalement.
-
Le transfert thermique
Q2 correspond au passage de 100 g de cire de l’état
solide à l’état liquide à la température constante de fusion de la
cire θf = 64 °
C.
-
Elle correspond à l’énergie
électrique cédée par le milieu extérieur par l’intermédiaire du
conducteur ohmique de puissance 200 W pendant la durée
Δt2 = 6 min.
-
Q2 =
Welec =
Pelec .
Δt2
-
Q2 = 200 × 6,0
× 60
-
Q2 ≈ 7,2 × 104
J 4.
Transfert thermique Qtot
nécessaire à la fusion de 100 g de cette cire.
-
Choix du système :
-
Si le système d’étude est : {cuve et
cire} :
-
Alors l’énergie totale est :
-
Qtot =
Q1 +
Q2
-
Qtot ≈ 2,5 ×
104 + 7,2 × 104
-
Qtot ≈ 9,7 ×
104 J
-
Maintenant, si le système d’étude est
la cire exclusivement :
-
Qtot
représente le transfert thermique suivant :
-
Premier temps on chauffe 100 g de
cire de 19 ° C à 64 ° C ;
-
Q’1 = m1
. ccire
. (θf – θa)
-
Q’1 = 0,100 ×
3,4 × 103 × (64
– 19)
-
Q’1 ≈ 1,53
× 104 J
-
Q’1 ≈ 1,5 × 104
J
-
Deuxième temps,
on fait fondre les 100 g de
cire
-
Q2 ≈ 7,2 × 104
J
-
Qtot =
Q’1 +
Q2
-
Qtot ≈ 1,5 ×
104 J + 7,2 × 104 J
-
Qtot ≈ 8,7 ×
104 J
►
Chaleur latente de changement
d’état :
-
L’énergie transférée lors d’un
changement d’état d’un kilogramme d’une espèce chimique est
l’énergie massique de changement d’état, notée L de cette
espèce.
-
Cette énergie est aussi appelée
chaleur latente de changement d’état.
-
Elle s’exprime en J. kg–1.
-
L’énergie Q transférée lors du
changement d’état d’une masse m de l’espèce est donnée par la
relation suivante :
-
En conséquence, la grandeur
Q2 ≈ 7,2 × 104 J permet de calculer la chaleur
latente de fusion Lf
de la cire d’abeille :
-
Q2 = m1
. Lf
-
-
La cire d'abeille est un mélange
complexe d'esters d’acides gras, d'acides gras et de composés
hydrocarbonés.
-
Un corps gras est un triester d'acide
gras et du glycérol.
-
Les corps gras sont encore appelés
triglycérides.
-
Le glycérol est un trialcool : le
propan-1, 2, 3 -triol.
-
Un acide gras est un acide
carboxylique à chaîne linéaire, saturée ou non, possédant en général
un nombre pair d'atomes de carbone, entre 4 et 22.
|
12)- Exercice 29 page 317 : Équation de Van der Waals :
|
Équation de Van der Waals : Un gaz ne peut être assimilé à un gaz parfait lorsque sa pression
devient trop importante. On parle alors de « gaz réels ». L’équation de Van der Waals
permet de mieux décrire un gaz réel que l’équation d’état des gaz parfaits :
Une correction est effectuée dans l’équation de Van der Waals sur
la pression et le volume, à l’aide de deux coefficients a et b qui dépendent
de la nature du gaz. 1.
Montrer que, lorsque le volume V de
gaz réel est très grand, l’équation d’état des gaz parfaits devient une très bonne
approximation de l’équation de Van der Waals. 2. On veut comparer le modèle du gaz parfait à celui du gaz réel de Van der Waals pour deux exemples, le néon Ne et le dioxyde de carbone CO2. Chacun de ces gaz
occupe une enceinte close de volume V = 5,00 L, à
une température T = 300,0 K, avec la même quantité de matière n = 1,00 mol. a.
Calculer la pression P de chacun de
ces gaz dans le cadre du modèle du gaz parfait. b.
Calculer de même la pression P’ de
chacun de ces gaz dans le cadre du modèle du gaz réel de Van der Waals. c.
Comparer P et P’. Lequel de
ces gaz se rapproche le plus du gaz parfait ? interpréter.
-
Données :
-
Constante des gaz parfaits :
R = 8,314 Pa . m3
. mol–1 . K–1.
-
Pour le néon :
-
a = 0,02135 Pa
. m6 . mol–2 et
b = 1,71 × 10–5
m3 . mol–1.
-
Pour le dioxyde de carbone :
-
a = 0,364 Pa
. m6 . mol–2 et
b = 4,267 × 10–5
m3 . mol–1. |
|
Équation de Van der Waals :
- Pour les corps purs :
-
-
TC :
Température critique du corps pur en kelvin (K).
- PC : Pression
critique du corps pur en pascal (Pa).
- R :
constante des gaz parfaits :
R = 8,314 Pa . m3
. mol–1 . K–1
-
- Diagramme
P =
f (T)
- Le point critique d’un corps pur est
le point du diagramme température-pression où s’arrête la courbe
d’équilibre liquide-vapeur.
- Le point triple du diagramme
température-pression est le point pour lequel l’état solide, l’état
liquide et l’état gazeux coexistent en équilibre.
-
Le néon est un gaz monoatomique dans les CNTP. -
À la pression atmosphérique, il se condense à 27 K et
se solidifie à 24,6 K. -
Le néon est un gaz extrêmement inerte. -
La couleur orange rougeâtre, que le néon émet (tubes
néon), est utilisé pour les enseignes lumineuses.
1.
Le volume V de gaz réel est très
grand.
-
Équation d’état des gaz parfaits :
-
P .
V =
n . R .
T
-
Équation
de Van der Waals :
-
-
Étude du terme
-
-
Étude du terme :
-
-
En conclusion :
-
2.
Comparaison des deux équations. a.
Valeur de la pression P de chacun de
ces gaz dans le cadre du modèle du gaz parfait.
-
b.
Valeur de la pression P’ de chacun de
ces gaz dans le cadre du modèle du gaz réel de Van der Waals.
-
Pression
P’ :
-
Relation :
-
-
Cas du néon :
-
-
Pour le dioxyde de carbone :
-
c.
Comparaison de P et P’.
-
Les différentes valeurs :
-
P ≈ 4,99 × 105
Pa ; P’Ne ≈
5,00 × 105 Pa ; P’CO2 ≈
4,89 × 105 Pa
-
P’Ne ≈
P
-
Le néon se rapproche le plus du gaz
parfait.
-
Interprétation :
-
Le néon est un gaz monoatomique alors
que le dioxyde de carbone est une molécule constituée de deux atomes
d’oxygène O et d’un atome
de carbone C.
-
Rayon de l’atome de néon :
RNe = 38 pm.
-
Rayon de l’atome de carbone :
RC = 70 pm
-
Rayon de l’atome d’oxygène :
RO = 60 pm
-
Caractéristiques
de la molécule de dioxyde de carbone :
-
La molécule de dioxyde de carbone est
plus grande que l’atome de néon.
-
Le néon, gaz monoatomique se
rapproche plus du modèle du gaz parfait que la molécule de dioxyde
de carbone. - De plus, le néon est un gaz rare.
- Les
interactions entre les atomes de néon sont négligeables.
►
Le gaz parfait :
-
Un gaz est dit parfait si la taille
de ses entités est négligeable devant la distance qui les sépare et
si les interactions entre elles sont négligeables. |
|||||||||||||||||||
|
|