|
|
Mouvements d'un système Exercices |
|
|
|
|
1)- Exercice 01 page 234 :Tracer un vecteur vitesse :
|
Tracer un vecteur vitesse : Quelques positions d’un système en mouvement sont représentées
sur le schéma suivant : La valeur de la vitesse v3 à l’instant t3
où le système est en M3 est 4,2 × 10–1
m . s–1. -
Reproduire le schéma et représenter le vecteur vitesse
de vitesse proposée : 1 cm
↔ 0,10 m . s–1. |
|
Tracer un vecteur vitesse :
-
Enregistrement :
-
Représentation du vecteur vitesse
-
Dans le cas présent, on connaît la
valeur de la vitesse :
-
v3 = 4,2 × 10–1
m . s–1 - Grâce à l’échelle de représentation, on détermine la valeur de la longueur du segment fléché du
représentant du vecteur vitesse :
-
Le segment fléché aura une longueur :
ℓv3
= 4,2
cm.
-
Pour tracer ce vecteur vitesse
- Origine : position occupée par le point mobile à l'instant considéré t3 c'est-à-dire le point M3.
-
Direction
: tangente à la trajectoire au point considéré : - On peut s’aider de la droite (M2 M4) - On trace la parallèle issue de
M3
à la droite (M2 M4)
.
-
Sens
: celui du mouvement à cet instant
-
Valeur
: celle de la vitesse à cet instant :
-
-
On connaît la valeur :
v3 = 4,2 × 10–1 m . s–1
-
Longueur
du représentant ℓv :
-
ℓv3
= 4,2
cm |
2)- Exercice 04 page 234 : Tracer un vecteur variation de vitesse :
|
Tracer un vecteur variation de vitesse : La chronophotographie du mouvement d’un ballon de basket est
représentée ci-dessous. La valeur v1 de la vitesse du ballon en M1
est 5,5 m . s–1. La valeur v2 de la vitesse du ballon en M2
est 4,6 m . s–1.
-
Représenter le vecteur variation de
vitesse
-
Échelle : 1,0
cm ↔ 1,0 m . s–1. |
|
Tracer un vecteur variation de vitesse :
-
Représentation du vecteur variation
de vitesse
-
-
Le vecteur vitesse
-
Origine
: M1.
-
Direction
: tangente à la trajectoire au point considéré :
-
On peut s’aider de la droite (M0M2)
-
On trace la parallèle issue de M1
à la droite (M0M2).
-
Sens
: celui du mouvement à cet instant
-
Valeur
: celle de la vitesse à cet instant :
-
v1 = 5,5 m . s–1
-
Longueur
du représentant ℓv :
-
ℓv3
= 5,5
cm
-
Le vecteur vitesse
-
Origine
: M2.
-
Direction
: tangente à la trajectoire au point considéré :
-
On peut s’aider de la droite (M1M3)
-
On trace la parallèle issue de M2
à la droite (M1M3).
-
Sens
: celui du mouvement à cet instant
-
Valeur
: celle de la vitesse à cet instant :
-
v2 = 4,6 m . s–1
-
Longueur
du représentant ℓv :
-
ℓv2
= 4,6
cm
-
On peut tracer ces deux vecteurs :
-
Tracé du vecteur variation de
vitesse
-
Origine
: M2.
-
Direction
:
-
Longueur
du représentant ℓΔv :
-
ℓΔv
≈
1,22 cm
-
Valeur du vecteur variation de
vitesse
:
-
Δv1→2 ≈ 1,2 m
. s–1
-
|
3)-
Exercice 06 page 235 : Connaître la direction et le
sens de ![]() :
:
|
Connaître la direction et le sens de
-
Pour les tableaux ci-dessous, relier
chaque schéma de
-
Plusieurs schémas peuvent accepter la
même réponse.
|
Correction :
-
Dans un référentiel donné, si un
système de masse m
constante est soumis à une ou plusieurs forces constantes, le vecteur variation de
vitesse
système pendant une durée très courte
Δt et la somme de ces
forces
par la relation :
Valeur de la force F en newton (N)
Valeur de la masse m en kilogramme (kg)
Valeur de la durée Δt en seconde (s)
-
Les vecteurs
Ou Il faut regarder les vecteurs
![]() de
ce
de
ce ![]() sont reliés
sont reliés

![]() et
et
![]() sont
colinéaires.
sont
colinéaires.
![]() et
et
![]()

![]()
4)-
Exercice 07 page 235 : Exploiter la somme des forces
![]() :
:
|
Exploiter la somme des forces Un mobile relié par un fil à un plot central fixe est lancé. Le fil reste tendu au cours du mouvement du mobile qui se déplace sans fortement sur un support horizontal. On a représenté ci-dessous les positions occupées par le mobile à intervalles de temps égaux ainsi que la somme des forces
à ce mobile en quatre positions A, B, C et
D. Schéma : 1.
Décrire le mouvement du mobile. 2.
Représenter le vecteur variation de vitesse
d’échelle aux positions A,
B, C et D. |
Exploiter la somme des forces 1.
Mouvement du mobile.
-
Le mobile est animé d’un mouvement
circulaire uniforme.
-
Il parcourt des distances égales
pendant des durées égales.
-
Il est toujours situé à la même
distance du plot central.
-
Il tourne autour du plot central
toujours à la même distance de celui-ci. 2.
Vecteur variation de vitesse
-
Dans un référentiel donné, si un
système de masse m
constante est soumis à une ou plusieurs forces constantes, le vecteur variation de
vitesse
pendant une durée très courte
Δt et la somme de ces
forces
Valeur de la force F en newton (N)
Valeur de la masse m en kilogramme (kg)
Valeur de la durée Δt en seconde (s)
-
Les vecteurs
-
Ils ont la même direction et le même
sens au cours du mouvement du mobile.
-
Tous les vecteurs
![]() :
:![]() aux positions A, B, C et D.
aux positions A, B, C et D.![]() de
ce système
de
ce système ![]() sont reliés par la relation :
sont reliés par la relation :

![]() et
et
![]() sont
colinéaires.
sont
colinéaires.![]() ont la même valeur au cours du mouvement du mobile.
ont la même valeur au cours du mouvement du mobile.![]()
5)- Exercice 08 page 235 : Connaître l’influence de la masse du système :
|
Connaître l’influence de la masse du système : Un système assimilé à un point matériel M de masse m
glisse sur le sol. Il est soumis aux forces représentées ci-dessous à la même
échelle. Schéma :
La force
1.
Schématiser la somme
2.
En déduire, d’après la relation approchée
et le représenter sans contrainte d'échelle. 3. Un autre système de masse 2 m est soumis à cette même somme des forces. Pour une même durée, comparer
les vecteurs variations de vitesse de ces deux systèmes. |
|
Connaître l’influence de la masse du système : 1.
Schéma de la somme
-
-
Première étape : on choisit une
origine : le point O.
-
Deuxième étape : on trace le vecteur
-
Elle est normale au support : les
frottements sont négligeables.
-
Troisième étape : on trace le vecteur
-
La force
-
Quatrième étape : on trace le vecteur
-
Le vecteur
-
Le vecteur résultante des forces :
-
Son origine est le point
O et son extrémité, l’extrémité du vecteur
-
Remarques : -
-
Les deux forces
des sens opposées :
-
-
Elles se compensent. 2.
Représentation du vecteur variation de
vitesse
-
Pour le mobile de masse
m :
-
-
-
Le vecteur
-
-
Schéma :
3.
Comparaison des vecteurs variations de
vitesse de ces deux systèmes.
-
Pour le mobile de masse
m :
-
-
Il est soumis à la somme des forces
suivantes :
-
-
- Pour le mobile de masse m’ = 2 m, soumis aux mêmes forces, pendant la même durée Δt :
-
-
-
En analysant les relations (1) et
(2) :
-
-
Le vecteur
-
Si la masse du système est deux fois
plus grande, alors le vecteur variation de vitesse
ceci pour la même somme des forces
|
6)- Exercice 10 page 236 : Planeur au décollage :
|
Planeur au décollage :
Avant d’effectuer son vol en toute autonomie, un planeur doit
être tracté par un avion afin de décoller et d’atteindre une altitude adaptée. On étudie la phase précédent le décollage pendant laquelle le
planeur, d’une position arrêtée, acquiert une vitesse tout en étant en contact avec le
sol. 1.
Première phase : a.
Décrire le mouvement d’un point M
modélisant le planeur dans un référentiel terrestre. b.
Schématiser, sans contrainte d’échelle,
quelques positions du point M à intervalles de temps égaux. 2.
Représenter, sans contrainte d’échelle, le
vecteur variation de vitesse
3. Le même avion tracte avec la même force un planeur plus léger que le planeur précédent. Comparer à la même date t
les vecteurs
|
|
Planeur au décollage : 1.
Première phase : a.
Mouvement d’un point M modélisant le
planeur dans un référentiel terrestre.
-
On considère que le planeur se
déplace sur un sol horizontal.
-
Au départ, le planeur est à l’arrêt,
puis il acquiert la vitesse
-
Dans le référentiel terrestre, le
planeur est animé d’un mouvement rectiligne accéléré. b.
Quelques positions du point M à
intervalles de temps égaux.
-
Chronophotographie du mouvement du
planeur.
-
Le point
M modélise le planeur :
-
Le planeur parcourt des distances de
plus en plus grandeurs pendant des durées égales Δt. 2.
Le vecteur variation de vitesse
-
Le vecteur
-
Ceci découle de la relation
approchée suivante :
-
3.
Comparaison même date t, des vecteurs
-
Si le même avion tracte avec la même
force
alors le vecteur variation de vitesse
-
Pour le planeur de masse
m :
-
-
Pour le planeur de masse
m’, avec m’ <
m :
-
-
En combinant les relations (1) et
(2) :
-
-
Pour une même durée Δt :
-
-
Comme
m’ <
m , alors :
-
-
Schéma :
|
7)- Exercice 16 page 237 : L’attraction gravitationnelle du Soleil :
|
L’attraction gravitationnelle du Soleil : On peut considérer que le mouvement de la Terre est circulaire
uniforme dans le référentiel héliocentrique et que le Soleil exerce une
force sur la Terre.
-
La schématisation du vecteur
variation de vitesse
-
Schéma :
-
Données :
-
Masse de la Terre :
MT = 6,0 × 1024
kg
-
Masse de la Terre :
MS = 2,0 × 1030
kg
-
Constante universelle de
gravitation : G = 6,67 ×
10–11 N . m2 . kg–2.
-
Distance Soleil-Terre :
dS–T = 1,5 ×
1011 m. |
|
L’attraction gravitationnelle du Soleil :
-
La schématisation du vecteur
variation de vitesse
-
Schéma : - Les mesures : (les mesures ont été effectuées avec le
logiciel PHOTOFILTRE)
-
Longueur du représentant du vecteur
variation de vitesse
-
ℓΔv ≈ 15,18 cm
-
Échelle :
-
7,30 cm ↔ 10 m . s–1.
-
Valeur de
Δv :
-
Autre calcul de
Δv :
-
Ceci à partir de la formule
approchée :
-
-
La force que subit la Terre :
-
C’est la force gravitationnelle
exercée par le Soleil sur la Terre.
-
-
Schéma :
-
-
Les vecteurs
-
Valeur de
Δv :
-
-
La schématisation du vecteur
variation de vitesse
|
8)- Exercice 18 page 238 : Une Histoire de pointage :
|
Une Histoire de pointage : On a réalisé la chronophotographie du mouvement d’une balle accrochée à un fil. L’intervalle de temps Δt entre deux images successives est
80 ms.
-
Schéma : 1.
Les vitesses : a.
Calculer les valeurs v5 et
v6 des vitesses aux positions 5 et 6. b.
Identifier les sources d’erreur dans la
détermination de v5 et v6. 2.
Tracer les vecteurs vitesses
3.
Construire le vecteur variation de vitesse 4.
Sans contrainte d’échelle, schématiser le
vecteur somme des forces
|
Une Histoire de pointage :
-
Schéma : 1.
Les vitesses : a.
Valeurs v5 et v6
des vitesses aux positions 5 et 6.
-
Valeur de la vitesse
v5 :
-
-
Mesures effectuées à l’aide du
logiciel PHOTOFILTRE :
-
Distance
M5M6
sur le schéma : d (M5M6)
≈ 3,27 cm
-
Échelle :
-
1,00 m → 14,18 cm
-
Valeur de la distance réelle
M5M6 : Schéma
Réel
3,27
cm
M5M6
14,18
cm
1,00
m
-
Valeur de la vitesse
v5 :
-
-
Valeur de la vitesse
v6 :
-
-
Mesures effectuées à l’aide du
logiciel PHOTOFILTRE :
-
Distance
M6M7
sur le schéma : d (M6M7)
≈ 2,80 cm
-
Échelle :
Idem
-
1,00 m → 14,18 cm
-
Valeur de la distance réelle
M6M7 : Schéma
Réel
2,80
cm
M6M7
14,18
cm
1,00
m
-
Valeur de la vitesse
v6 :
-
-
Erreur sur les pointages.
-
Erreur sur la mesure des distances.
-
Erreur sur la mesure de l’échelle.
-
Erreur sur la mesure des durées. 2.
Tracé des vecteurs vitesses
-
Échelle utilisée : 1,0 m . s–1
↔ 1,0 cm
-
Longueur du représentant de
-
Longueur du représentant de
-
Schéma :
-
Les vecteurs
-
Ils sont perpendiculaires au fil. 3.
Vecteur variation de vitesse
-
L’origine de ce vecteur est le point
M6.
-
Schéma : 4.
Schéma du vecteur somme des forces
-
La balle est soumise à :
-
La tension du fil
-
Son poids
-
-
De la relation approchée suivante :
-
-
On déduit que le vecteur
le vecteur variation de vitesse
-
Les différentes forces :
-
Le pendule simple :
Vidéos
Pendule simple
(vitesse, accélération)











![]() et
et
![]() .
. ![]() :
ℓv5 ≈ 2,9 cm
:
ℓv5 ≈ 2,9 cm![]() :
ℓv6 ≈ 2,5 cm
:
ℓv6 ≈ 2,5 cm![]() et
et
![]() sont tangents à la
trajectoire.
sont tangents à la
trajectoire. ![]() :
:
![]() qui s’exercent sur la balle
dans la position 6.
qui s’exercent sur la balle
dans la position 6.![]()
![]()
![]()

![]() a même
direction et même sens que
a même
direction et même sens que ![]() dans la
position 6.
dans la
position 6.![]()
9)- Exercice 22 page 239 : Ski de vitesse :
|
Ski de vitesse :
-
Déterminer les caractéristiques de la
force de frottement qui s’exerce sur le skieur dans la zone de chronométrage. A.
Le kilomètre lancé. Le ski de vitesse a pour but d’atteindre la valeur de vitesse la
plus élevée possible dans une zone de 100 m appelée zone de chronométrage.
B.
La zone de chronométrage. Le skieur entre dans la zone de chronométrage après un élan de quelques centaines de mètres. On suppose que, dans cette zone, le skieur a
un mouvement rectiligne uniforme. La piste fait un angle de 20 ° avec l’horizontale. C.
Modélisation dans actions mécaniques qui
s’exercent sur le skieur. Le skieur est modélisé par un point S. La force exercée par la piste sur le skieur peut se décomposer
en :
-
Une force perpendiculaire à la piste,
appelée réaction normale
-
Une force parallèle à la piste,
appelée force de frottement
Sur cette construction, les vecteurs sont représentés sans souci
d’échelle.
-
Données :
-
Intensité de la pesanteur
g = 10 N . kg–1.
-
Masse du skieur et de son
équipement : m = 90 kg.
-
La réaction normale de la piste a
pour valeur constante RN
= 845 N. |
Ski de vitesse :
-
Détermination des caractéristiques de
la force de frottement
-
Dans le texte : « On suppose que,
dans cette zone, le skieur a un mouvement rectiligne uniforme. »
-
Réciproque du principe
d’Inertie : Si le vecteur
vitesse
alors le système est soumis à de forces qui se compensent.
-
Le skieur est représenté par le point
matériel S.
-
Le skieur est soumis :
-
À son poids
Point
d’application : S
Direction : verticale passant par S
Sens : haut vers bas
Valeur : P =
m . g
=> P ≈ 900 N
-
À la réaction du support
Point
d’application : S
Direction : perpendiculaire à la piste
Sens : bas vers haut
Valeur : RN = 845 N
-
À la force de frottement
Point
d’application : S
Direction : parallèle à la piste
Sens : opposé au mouvement
Valeur : f
= ?
-
L’application de la réciproque du
principe d’inertie à la situation du skieur permet de déterminer les caractéristiques de la force de
frottement
-
La réciproque du principe d’inertie
permet d’affirmer que le skieur est soumis à des actions mécaniques dont les effets se compensent :
-
-
On peut réaliser une construction
graphique avec l’échelle suivante :
-
Échelle : 100 N ↔ 1,00 cm
-
Longueur du représentant du vecteur
poids - ℓP
= 9,00 cm
-
Longueur du représentant du vecteur
réaction de la piste
- ℓRN
= 8,45 cm
-
À partir d’un point
O, choisi comme origine, on trace le vecteur poids
-
À la suite du vecteur poids
-
Le vecteur force de frottement
-
Construction :
-
Mesure de la longueur du représentant
du vecteur frottement
-
ℓf ≈ 3,1 cm
-
Valeur de la force de frottement :
-
f ≈ 3,1 × 102
N
-
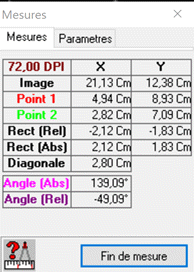
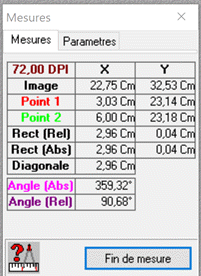
Mesures avec Photofiltre sur le
schéma :
-
Échelle : Force de
frottement :
-
Valeur
de la force
f : Longueur
Valeur
9,32
cm
f
2,96
100 N - Caractéristiques du vecteur force de
frottement
Point
d’application : S
Direction : parallèle à la piste
Sens : opposé au mouvement
Valeur : f
≈
315 N
![]() qui
s’exerce sur le skieur dans la zone de chronométrage.
qui
s’exerce sur le skieur dans la zone de chronométrage.
![]() d’un
système ne varie pas au cours du temps,
d’un
système ne varie pas au cours du temps, ![]()
![]() :
:
![]()
![]() :
:
![]()
![]() :
:
![]()
![]() .
.![]()
![]() :
: ![]() :
: ![]() , on trace
le vecteur réaction de la piste
, on trace
le vecteur réaction de la piste
![]() .
.![]() a pour
origine l’extrémité du vecteur
a pour
origine l’extrémité du vecteur
![]() et
pour extrémité le point O.
et
pour extrémité le point O.![]() : (avec Word)
: (avec Word)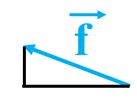

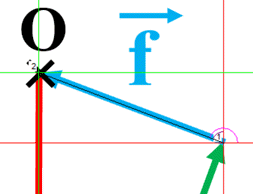


![]() :
:
![]()
![]()
|
|