|
Phys. N° 9 |
Le Gaz Parfait : Exercices. correction. |
|
|
Programme 2010 : Programme 2020 : |
|
Exercices 2005-2006 Physique et Chimie seconde Collection DURANDEAU HaCHETTE |
|
|
Physique et Chimie seconde Collection Microméga Hatier Ancienne édition |
|
|
|
I - Exercice 5 page 176 : Déterminer l’évolution de la pression :
|
Énoncé : 1)- On suppose la température et la quantité
de matière constantes. -
Proposer une expérience permettant de déterminer
l’évolution de la pression en fonction du volume. 2)- Parmi les propositions suivantes,
lesquelles sont vraies ? a)-
Pour une quantité donnée de gaz, le produit p . V, à
température constante, est indépendant de la pression. b)-
Pour une quantité donnée de gaz, le produit p . V, à
température constante, est indépendant du volume. c)-
Pour une quantité donnée de gaz et à température constante,
la pression p est proportionnelle au volume
V.
|
|
Correction :
1)- Expérience permettant de déterminer
l’évolution de la pression en fonction du volume : -
Seringue reliée à un manomètre :
-
Une quantité d’air est enfermé dans la seringue
graduée en mL. -
L’embouchure de la seringue est fermée par un capteur
de pression. -
Le capteur de pression est gradué en hPa. -
Il donne la pression absolue. -
On déplace lentement le piston de la seringue. -
Pour différentes positions du piston, on relève les
valeurs du volume V et de la pression p du gaz. -
On fait une dizaine de mesures. 2)- Les propositions vraies : -
Énoncé de la Loi de Boyle – Mariotte. - À température constante, pour une quantité donnée de gaz, - le produit de la pression p par le volume V
occupé par le gaz est constant : -
p.V = k. -
En conséquence, propositions vraies sont les
suivantes : b)-
Pour une quantité donnée de gaz, le produit p . V, à
température constante, est indépendant de la pression. c)- Pour une quantité donnée de gaz, le produit p . V, à température constante, est indépendant du volume.
|
II - Exercice 6 page 176 : Appliquer la loi de Boyle – Mariotte
|
Énoncé : À la température ambiante de 20 °C, on relie l’extrémité d’un seringue, contenant 50 mL d’air, à un manomètre qui
indique une pression de 1,0 bar. 1)- Quelle est la pression de
l’air enfermé si, en poussant le piston, on ramène son volume à une
valeur de 30 mL ? 2)- Quel est
le volume occupé par l’ait enfermé si on ramène la pression à une
valeur de 0,90 bar ?
|
|
Correction : 1)- Valeur de
la pression p2 de l’air enfermé pour un volume
V2 = 30 mL ?
-
On considère que la température n’a
pas changée au cours de l’expérience :
-
En conséquence, on peut utiliser la
loi de Boyle – Mariotte :
-
p . V = k
-
État initial : p1 =
1,0 bar et V1 = 50 mL
-
État final : p2 = ?
bar et V2 = 30 mL
-
Il n’est pas nécessaire de convertir
puisque les volumes sont exprimés dans la même unité :
-
2)- Valeur du
volume occupé par l’ait enfermé si on ramène la pression à une
valeur de 0,90 bar :
-
État initial : p1 =
1,0 bar et V1 = 50 mL
-
État final : p3
= 0,90 bar et V3 = ?
-
|
III - Exercice 7 page 176 : Trouver la relation entre la pression et la température
|
Énoncé : On dispose d’un ballon, de bouchons à
plusieurs trous, d’un chauffe-ballon et de tous les capteurs
nécessaires. 1)- Schématiser le dispositif expérimental permettant d’étudier l’évolution de la pression avec la température, à volume et quantité de matière constants 2)- À 20 °C, la pression mesurée est 1,00 bar
et elle est de 1,12 bar à la température de 50 °C. a)-
La pression est-elle proportionnelle à la température θ
en °C. b)-
La pression est-elle proportionnelle à (θ + 273) ? c)-
Que représente la grandeur (θ + 273) ?
|
|
Correction : 1)- Schéma du dispositif expérimental permettant d’étudier l’évolution de la pression avec la température, à volume et quantité de matière constants :
2)- Questions : a)-
La pression est-elle proportionnelle à la température θ
en °C. -
La pression p n’est pas proportionnelle à la
température θ en °C. -
Le gaz parfait est un modèle. -
Pour un gaz réel
-
Dans le cas présent, on travaille à volume V
constant et à quantité de matière n constante : -
On tire : -
-
La grandeur T représente la température
absolue : -
T = (θ + 273) -
Ainsi : -
-
Conclusion : La pression p n’est pas
proportionnelle à la température θ. b)-
La pression est-elle proportionnelle à (θ + 273) ? -
La pression p proportionnelle à la température
absolue T = (θ + 273) -
c)-
Que représente la grandeur (θ + 273) ? -
La grandeur (θ + 273) représente la température
absolue T.
|
IV - Exercice 12 page 177 : Utiliser un volume molaire
|
Énoncé : Une bouteille de gaz butane, utilisée dans une habitation, contient 13 kg de gaz liquéfié. La masse molaire du butane est égale à 58 g / mol. 1)- Calculer
la quantité de matière de gaz contenue dans la bouteille. 2)- Calculer
le volume molaire du butane, à 25 °V sous la pression de 1,0 bar. 3)- Quel
volume de gaz, pris à 25 °C, et sous la pression de 1,0 bar, est
disponible ?
-
Donnée : la constante des gaz
parfaits : R = 8,31
S.I.
|
|
Correction : 1)- Quantité
de matière n, de gaz, contenue dans la bouteille.
-
2)- Volume
molaire Vm du butane, à 25 °V sous la pression de
1,0 bar.
-
1 bar = 105 Pa
-
3)- Volume de
gaz V, pris à 25 °C, et sous la pression de 1,0 bar,
disponible :
-
V = n . Vm
-
V ≈ 2,2
× 102
× 25
-
V ≈ 5,6
× 103 L
-
V ≈ 5,6 m3
|
V - Exercice 18 page 178 : Un briquet pour déterminer la masse molaire du butane
|
Énoncé : Les briquets à gaz contiennent du butane liquide. La pesée d’un briquet a donné une masse m = 20,51 g. Grâce à un tuyau souple, de faible section et adapté à l’orifice de sortie du gaz, on recueille par déplacement d’eau un volume V = 1,5
L de butane dans une bouteille en matière plastique. On pèse alors le briquet : sa masse m’ = 16,93 g. 1)- Faire un schéma de l’expérience. 2)- Au cours de l’expérience, la pression du gaz recueilli est égale à la pression atmosphérique : p = 1020 hPa et sa température θ = 23,0 °C. Calculer : a)-
La quantité de matière de gaz qui s’est échappée du briquet. b)-
La masse de butane correspondante. 3)- En déduire la masse molaire du butane. La comparer à celle
déterminée à l’aide de sa formule brute C4H10. Données : -
R = 8,314 S.I : masses molaires atomiques C
(12 g / mol) et H (1,0 g / mol)
|
|
Correction : 1)- Schéma de l’expérience. -
Le remplissage de la bouteille :
2)- Calcul : a)-
Quantité de matière de gaz qui s’est échappée du briquet. -
Dans le cas présent, il faut utiliser l’équation
d’état des gaz parfaits : -
b)-
La masse de butane mbut correspondante. -
Les pesées :
-
mbut = m – m’ ≈ 20,51
– 16.93 -
mbut ≈ 3,58 g 3)- En déduire la masse molaire du butane. La
comparer à celle déterminée à l’aide de sa formule brute C4H10. -
Masse molaire du butane à partir de l’expérience : -
-
Masse molaire à partir des données : -
M = 4 M (C) + 10 M (H)
= 4
× 12 + 10
× 1,0 -
M ≈ 58 g / mol -
Le résultat est cohérent avec les données de
l’exercice. -
On peut déterminer le « pourcentage d’erreur » avec la
relation suivante :
-
La précision est très bonne !
|
VI - Exercice 23 page 179 : Boyle et Mariotte avaient-ils raison ?
|
Énoncé : E. Mariotte (1620– 1684), physicien français, vérifie en 1679 la loi déjà énoncée par R. Toxneley, physicien anglais en 1661 à partir de
l’expérience de R. Boyle (1627 – 1691) : À température constante, la pression d’un gaz est
inversement
proportionnelle à son volume. 1)-
Terminologie : a)-
Comment peut-on qualifier ce gaz ? b)-
Que signifie l’expression
inversement proportionnel ? c)-
Traduire cette phrase par une
expression littérale. 2)- On enferme ce gaz dans une enceinte fermée, reliée à un manomètre et dont on peut faire varier le volume. On réalise, à température
constante, une série de mesures dont les résultats sont regroupés
dans le tableau suivant :
Pour exploiter les résultats, Sébastien choisit de représenter la pression p en fonction du volume V. Malika préfère
représenter p en
fonction du quotient 1/V. Choisir la méthode la mieux adaptée et
réaliser la représentation graphique. 3)- À propose
du graphique : a)-
Le graphique tracé montre-t-il que le
gaz suit la loi de Boyle – Mariotte ? b)-
Déterminer, à partir du graphique, la
valeur du produit p . V. 4)-
Exploitation du graphique : a)-
Déterminer la pression du gaz lorsque
le volume est égal à 54 cm3. b)-
Déterminer le volume du gaz sous la
pression de 1,50 bar.
|
|
Correction :
1)-
Terminologie : a)-
Un qualificatif pour le gaz :
-
Le gaz étudié est considéré comme
parfait. b)-
Signification
de l’expression inversement
proportionnel :
-
Cela signifie que lorsque la pression
p du gaz est multipliée par 2, alors le volume V du
gaz est divisé par 2. - De façon plus générale, cela signifie que lorsque la pression p du gaz est multipliée par la grandeur k,
alors le volume V du gaz est divisé par la
grandeur k.
-
En conséquence, le produit de p
par v est égal à k. c)-
Traduction cette phrase par une
expression littérale :
-
Relation :
-
2)- Graphique
le mieux adapté : - La représentation p = f (V) donne une courbe qui n’est pas facile à exploiter. Il est
délicat de trouver la relation qui lie p et V. - Dans le cas de la représentation p = f (1/V),
la représentation donne une droite qui
passe par l’origine si le gaz suit la loi de Boyle – Mariotte.
-
Ce graphe est nettement plus facile à
exploiter et on peut en déduire la relation qui liée p et 1/V.
-
Il suffit de déterminer la valeur du
coefficient directeur a de la droite moyenne tracée.
-
Visualisation des deux graphes :
-
Tableau de valeurs :
-
On obtient une courbe délicate à
exploiter (exploitation avec Excel en -dessous).
3)- À propose
du graphique : a)-
Loi de Boyle – Mariotte :
-
Pour le graphe p = f
(1/V), les points sont sensiblement alignés.
-
La droite moyenne passe par
l’origine.
-
On en déduit que le gaz suit la loi
de Boyle – Mariotte :
-
À
température constante, la pression d’un gaz est inversement
proportionnelle à son volume.
-
Relation :
-
-
Le coefficient k est égal au
coefficient directeur de la droite moyenne tracée.
-
-
En utilisant le fait que :
-
1 bar = 105 Pa et 1 cm3
= 10–6 m3
-
k = a ≈ 7,9 Pa . m3
-
Pour vérifier cette valeur, on peut
faire une étude statistique avec Excel.
-
Sélectionner le graphique sur Excel,
faire un clic droit
-
Sélectionner « Ajouter une courbe de
tendance »
-
Comme option, choisir « Linéaire »,
puis cocher :
-
Afficher l’équation sur le
graphique
-
Afficher le coefficient de
détermination (R2) sur le graphique.
-
Dans le cas présent : y ↔ p
et x ↔ 1/V :
-
La relation physique : p ≈
79,19 . (1/V)
-
Avec a ≈ 79 bar . m3
-
En utilisant le fait que :
-
1 bar = 105 Pa et 1 cm3
= 10–6 m3
-
k = a ≈ 7,9 Pa . m3 b)-
La valeur du produit p . V.
-
On tire de l’expression précédente :
p . V ≈ 7,9 Pa . m3 4)-
Exploitation du graphique : a)-
Valeur de la pression du gaz lorsque
le volume est égal à 54 cm3.
-
On peut utiliser la relation :
p . V ≈ 79 bar
. cm3
-
b)-
Valeur du volume du gaz sous la
pression de 1,50 bar.
-
On peut utiliser la relation :
p . V ≈ 79 bar
. cm3
-
-
Remarque avec le graphique p =
f (V), on peut faire une détermination graphique.
|
Loi de Mariotte :
Tableau de valeurs : le volume initial d'air dans la seringue est : Vi = 30 mL à la pression atmosphérique : patm = 963 hPa.
|
V
mL |
p
hPa |
1 / V
L-1 |
|
15 |
1785 |
66,67 |
|
20 |
1393 |
50,00 |
|
25 |
1139 |
40,00 |
|
30 |
963 |
33,33 |
|
35 |
826 |
28,57 |
|
40 |
727 |
25,00 |
|
45 |
644 |
22,22 |
|
50 |
576 |
20,00 |
|
55 |
521 |
18,18 |
|
60 |
475 |
16,67 |
|
p
Pa |
1 / V
m–3 |
|
1,79E+05 |
6,67E+04 |
|
1,39E+05 |
5,00E+04 |
|
1,14E+05 |
4,00E+04 |
|
9,63E+04 |
3,33E+04 |
|
8,26E+04 |
2,86E+04 |
|
7,27E+04 |
2,50E+04 |
|
6,44E+04 |
2,22E+04 |
|
5,76E+04 |
2,00E+04 |
|
5,21E+04 |
1,82E+04 |
|
4,75E+04 |
1,67E+04 |
Cliquer sur l'image pour l'agrandir
Tracé 1 : Pression en fonction du volume : p = f (V)
Cliquer sur l'image pour l'agrandir
Tracé 2 : Pression en fonction de l'inverse du volume : p = f (1 / V)
Cliquer sur l'image pour l'agrandir
- Relation liant p et V :
-
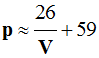
- Une seringue contient 18 cm 3 d’air à la pression normale.
- On bouche l’extrémité de la seringue et on pousse le piston de façon à réduire le volume gazeux à 6,0 cm 3.
- On suppose que la température reste constante.
- Quelle est alors, en pascals, la pression du gaz dans la seringue ?
- Pression du gaz dans la seringue :
|
État
1 |
|
État
2 |
|
V1
= 18 cm3 |
Transformation à
température constante |
V2
= 6,0 cm3 |
|
p1
= 1013 hPa |
|
p2
= ? |
- On utilise la Loi de Mariotte car la transformation se fait à température constante : p.V = cte
- En conséquence :
|
p1 . V1 = p2 . V2 |
|||
|
|
|||
|
|
|||
|
p2 = |
p1 . V1 |
||
|
|
|
|
|
|
V2 |
|
||
|
|
1,013 × 105 × 18 |
||
|
p2 = |
|
||
|
|
6,0 |
||
|
|
|||
|
p2 ≈ |
3,0 × 105 Pa |
||
Calculer le volume occupé à 20 °C et pour une pression de 1,0 × 105 Pa par une masse de 100 g de chacun des gaz suivants.
a)- L’argon (gaz monoatomique Ar).
- Volume occupé par l'argon à 20 °C :
- On utilise la relation du gaz parfait :
|
p . V = n . R . T |
{ |
p pression en pascal (Pa) |
|
V volume en mètre cube (m3) |
||
|
n quantité de matière en mole (mol) |
||
|
T température absolue en kelvin (K) |
|
Données |
p = 1,0 × 105 Pa |
|
V volume en mètre cube (m3) |
|
|
n ≈ 2,5 mol |
|
|
T = (273,15 + 20) K |
|
|
R ≈ 8,31 J . K– 1 . mol– 1 |
- En conséquence :
|
V = |
n . R . T |
||
|
|
|
|
|
|
p |
|
||
|
|
2,5 × 8,31 × 293,15 |
||
|
V = |
|
||
|
|
1,0 × 105 |
||
|
|
|||
|
V ≈ |
6,1 × 10 – 2 m3 |
||
|
V ≈ |
61 L |
||
b)- Le dioxygène (gaz diatomique O2).
- Il faut calculer la masse molaire et la quantité de matière n
- Volume occupé par le dioxygène à 20 °C :
|
V = |
n . R . T |
m |
|
|
|
et n = |
|
|
|
p |
|
M |
|
|
|
m . R . T |
||
|
V = |
|
||
|
|
p . M |
||
|
|
|||
|
100 x 8,31 x 293,15 |
|||
|
V = |
|
||
|
|
1,0 x 10 5 x 32 |
||
|
|
|||
|
V ≈ |
7,6 x 10 – 2 m 3 |
||
|
V ≈ |
76 L |
||
c)- Le dioxyde de carbone (gaz triatomique CO2).
- Volume occupé par le dioxyde de carbone à 20 °C :
|
V = |
n . R . T |
m |
|
|
|
et n = |
|
|
|
p |
|
M |
|
|
|
m . R . T |
||
|
V = |
|
||
|
|
p . M |
||
|
|
|||
|
100 x 8,31 x 293,15 |
|||
|
V = |
|
||
|
|
1,0 x 10 5 x 44 |
||
|
|
|||
|
V ≈ |
5,5 x 10 – 2 m 3 |
||
|
V ≈ |
55 L |
||
d)- L’hexafluorure de soufre SF6, gaz avec lequel sont gonflées les balles de tennis.
- Volume occupé par l'hexafluorure de soufre à 20 °C :
|
V = |
n . R . T |
m |
|
|
|
et n = |
|
|
|
p |
|
M |
|
|
|
m . R . T |
||
|
V = |
|
||
|
|
p . M |
||
|
|
|||
|
100 x 8,31 x 293,15 |
|||
|
V = |
|
||
|
|
1,0 x 10 5 x 146 |
||
|
|
|||
|
V ≈ |
1,7 x 10 – 2 m 3 |
||
|
V ≈ |
17 L |
||
Une bouteille contient du gaz butane C4H10 comprimé surmontant du butane liquéfié.
La bouteille est munie d’un manomètre et d’un détendeur.
a)- Quels sont les rôles d’un manomètre et d’un détendeur ?
- Le manomètre permet de mesurer la pression d’un gaz et le détendeur permet de détendre le gaz.
- Il abaisse la pression du gaz comprimé à la pression atmosphérique.
- Si le manomètre est placé avant le détendeur, il mesure la pression du gaz à l’intérieur de la bouteille.
- Si le manomètre est placé après le détendeur, il mesure la pression du gaz à la sortie de la bouteille.
b)- Le contenu de la bouteille a une masse de 12 kg. Quelle est la quantité de matière correspondante ?
- Quantité de matière de butane :
|
n = |
m |
||
|
|
|
(1) |
|
|
M |
|
|
|
|
|
12 × 1000 |
||
|
n = |
|
||
|
|
58 |
||
|
|
|||
|
n ≈ |
2,1 × 10 2 mol |
||
c)- En admettant que la totalité du contenu de la bouteille puisse être utilisée sous forme de butane gazeux à 20 °C et à la pression atmosphérique de 105 Pa, quel est le volume de gaz disponible ?
|
Données |
p = 1,0 × 105 Pa |
|
V volume en mètre cube (m3) |
|
|
n ≈ 2,1 × 102 mol |
|
|
T = (273,15 + 20) K |
|
|
R ≈ 8,31 J . K– 1 . mol– 1 |
|
V = |
n . R . T |
||
|
|
|
(2) |
|
|
p |
|
||
|
|
2,7 × 102 × 8,31 × 293,15 |
||
|
V = |
|
||
|
|
1,0 × 10 5 |
||
|
|
|||
|
V ≈ |
5,0 m3 ou 5,1 m3 |
||
|
Suivant la méthode de calcul. Si on fait les calculs sans arrondir, on obtient le premier résultat |
|||
- Une masse donnée d’un gaz est considérée dans 3 états successifs :
- État 1 caractérisé par p1, V1, T1.
- État 2 caractérisé par p2, V2, T2.
- État 3 caractérisé par p3, V3, T3.
- On donne : p1 = 1,0 x 10 5 Pa, V1 = 2,0 L et T1 = 300 K.
a)- Le passage de l’état 1 à l’état 2 s’effectue à pression constante par une élévation de température de 20 K.
- Déterminer p2, V2, T2.
- Le passage se fait à pression constante : p1 = p2 =1,0 x 10 5 Pa
- La température augmente de 20 K : T2 = T1 + 20 = 320 K
- On utilise la relation des gaz parfaits :
|
p . V = n . R . T => |
V |
n . R |
||
|
|
= |
|
= cte |
|
|
T |
p |
- On en déduit que :
|
V1 |
|
V2 |
|
|
= |
|
|
T1 |
|
T2 |
|
V2 = |
||
|
T2 |
||
|
|
. V1 |
|
|
T1 |
|
|
|
|
320 |
|
|
V2 = |
|
– 2,0 |
|
|
300 |
|
|
|
||
|
V2 ≈ |
2,1 L |
|
b)- Le passage de l’état 2 à l’état 3 s’effectue à température constante par une augmentation de pression de 1,0 × 104 Pa.
- Déterminer p3, V3, T3.
- Le passage se fait à température constante : T3 = T2 =320 K.
- La pression augmente de 104 Pa :
- p3 = p2 + 1,0 × 10 4 = 1,1 × 105 Pa .
- On peut utiliser la Loi de Mariotte car la transformation se fait à température constante :
|
p3 . V3 = p2 . V2 |
|||
|
|
|||
|
|
|||
|
V3 = |
p2 . V2 |
||
|
|
|
|
|
|
p3 |
|
||
|
|
1,0 × 105 × 2,1 |
||
|
V3 = |
|
||
|
|
1,1 × 105 |
||
|
|
|||
|
V3 ≈ |
1,9 L |
||
- On considère deux espèces chimiques gazeuses, puis leur mélange.
- On admet que tos les gaz peuvent être modélisés par le gaz parfait.
- Une quantité de matière n1 du premier gaz a un volume V1, une pression p1 et une température absolue T1.
- Une quantité de matière n2 du second gaz a un volume V2, une pression p2 et une température absolue T2.
- Le mélange de ces deux gaz est effectué dans un volume V, la pression et p et la température absolue T.
a)- Quel est la quantité de matière n du mélange ?
- Comme on modélise les deux espèces chimiques gazeuses par le gaz parfait,
- on peut considérer que le mélange de gaz parfaits se comporte comme un gaz parfait de quantité de matière :
- n = n1 + n2.
b)- Écrire l’équation d’état pour chacune des espèces gazeuses, puis pour le mélange.
- Pour l ‘espèce gazeuse 1 : p1 . V1 = n . R . T1
- Pour l ‘espèce gazeuse 2 : p2 . V2 = n . R . T2
- Pour le mélange : p . V = n . R . T
c)- Dans le cas où p = p 1 = p 2 et T = T 1 = T 2, déterminer le volume V du mélange en fonction des volumes V1 et V2.
- En conséquence :
- p 1 . V 1 = n . R . T 1,
- p 2 . V2 = n . R . T 2 et
- p . V = n . R . T avec : n = n1 + n2.
- ![]() ,
,
![]() et
et
![]()
- ![]()
d)- Dans le cas où
- V = V1 = V2 et T = T1 = T2, établir une relation entre les trois pressions p, p1 et p2 .
- (Cette relation est appelée Loi de Dalton)
- Pour l'espèce gazeuse 1 :
- p1 . V = n1 . R . T
- Pour l'espèce gazeuse 2 :
- p2 . V = n2 . R . T
- Pour le mélange :
- p . V = n . R . T
- ![]() ,
,
![]() et
et
![]()
- ![]()