|
|
Modélisation macroscopique de l'évolution d'un système Exercices |
|
|
|
|
|
QCM r
Les facteurs cinétiques
|
1)- Exercice 02 page 84 : Justifier une méthode expérimentale :
|
Justifier une méthode expérimentale : On suit l’évolution de la concentration en diiode de quatre mélanges réactionnels (A, B, C et D) lors de la réaction entre le peroxyde d’hydrogène H2O2
(aq), les ions iodure I– (aq) et les ions
hydrogène H+ (aq). L’équation s’écrit : H2O2 (aq) + 2
I–
(aq) + 2 H+ (aq) → I2 (aq)
+ 2 H2O (ℓ) Le diiode est la seule espèce colorée. Les quantités initiales de réactifs dans les mélanges
réactionnels de volumes égaux sont données ci-dessous :
Pour chaque mélange, on
trace l’évolution de la concentration en diiode au cours du
temps : 1.
Justifier l’utilisation d’un
spectrophotomètre pour suivre l’évolution de la concentration en
diiode dans les mélanges. 2.
En comparant les courbes deux à deux,
montrer l’influence de la concentration sur la rapidité d’évolution
d’un système. |
|
Justifier une méthode expérimentale : 1.
Utilisation d’un spectrophotomètre pour
suivre l’évolution de la concentration en diiode dans les mélanges.
-
Le diiode est la seule espèce
colorée.
-
On peut mesurer l’absorbance du
mélange réactionnel au cours du temps.
-
On peut utiliser cette méthode
lorsqu’une espèce colorée se forme ou disparaît au cours de la
réaction.
-
Le diiode, qui donne à la solution
une teinte jaune-orangé, est la substance absorbante.
-
À l’instant
t = 0 (il faut faire
démarrer le chronomètre), on réalise le mélange réactionnel.
-
Puis, on prélève 2 mL du mélange
réactionnel à l’aide d’une seringue que l’on les verse dans la cuve
du spectrophotomètre.
-
on mesure la valeur de
l’absorbance à différentes dates.
-
Pour connaître la concentration en
diiode au cours du temps, on utilise la loi de Beer-Lambert.
-
Comme la concentration en diiode est
faible, l’absorbance de la solution est proportionnelle à la
concentration en diiode :
-
A =
k [I2]
-
On peut ainsi tracer la courbe [I2]
= f (t) 2.
Influence de la concentration sur la
rapidité d’évolution d’un système.
-
On étudie les courbes deux à deux en
faisant en sorte qu’un seul paramètre soit modifié.
-
Courbes
A
et
C :
-
C’est la quantité de matière initiale
de diiode qui change entre l’expérience
A
et l’expérience B.
-
n0 (I–)A
> n0 (I–)B :
n0 (I–)A =
2
n0 (I–)B
-
Exploitation graphique :
-
La courbe
A
se situe au-dessus de la courbe
B.
-
Le diiode se forme plus vite dans
l’expérience
A que dans l’expérience
B.
-
Courbes
B
et
C :
-
C’est la quantité de matière initiale
de H2O2 (aq) entre l’expérience
B et l’expérience
C.
-
n0 (H2O2)B
> n0 (H2O2)C : n0 (H2O2)B
=
2
n0 (H2O2)C
-
Exploitation graphique :
-
La courbe
B
se situe au-dessus de la courbe
C.
-
Le diiode se forme plus vite dans
l’expérience
B que dans l’expérience
C.
-
Courbe
A
et
D :
-
C’est la quantité de matière initiale
de H+
(aq) entre l’expérience
A et l’expérience
D.
-
n0 (H+)A
> n0 (H+)D :
n0 (H+)A
=
2
n0 (H+)D
-
Exploitation graphique :
-
La courbe
A
se situe au-dessus de la courbe
D.
-
Le diiode se forme plus vite dans
l’expérience
A que dans l’expérience
D.
-
La concentration des réactifs est un
facteur cinétique.
-
Quand la concentration des réactifs
diminue, le système chimique évolue plus lentement et inversement. |
2)- Exercice 04 page 84 : Étudier l’influence d’un catalyseur :
|
Étudier l’influence d’un catalyseur : La rhodamine, utilisée comme colorant dans l’industrie du papier, doit être éliminée des effluents industriels. Pour étudier sa photo-dégradation en présence d’un catalyseur, le dioxyde de titane, on expose à la lumière une solution de rhodamine. On relève l’absorbance A de la solution au cours du temps. Sur le graphique ci-dessous, le rapport
l’absorbance A0 de la solution avant
l’exposition à la lumière (t = 0 s). 1.
Justifier à l’aide du graphique que le
dioxyde de titane est bien un catalyseur et non un réactif. 2.
Déterminer l’influence de la concentration
en catalyseur sur la cinétique de la réaction.
-
Représentation graphique :
-
Données :
-
On compte la rhodamine
6G, la rhodamine B et la
rhodamine 123.
|
|
Étudier l’influence d’un catalyseur : 1.
Le dioxyde de titane est bien un catalyseur
et non un réactif.
-
Le catalyseur :
-
Un catalyseur est une espèce chimique
qui accélère une réaction chimique.
-
Au cours de la transformation, il est
consommé puis régénéré.
-
En conséquence, sa formule n’apparaît
pas dans l’équation de la réaction.
-
Lorsque l’on analyse la
courbe verte, on remarque que le
dioxyde de titane n’est pas présent et pourtant la réaction a bien lieu.
-
D’autre part en présence de dioxyde
de titane, la réaction évolution plus rapidement.
-
Le dioxyde de titane est bien un
catalyseur de la réaction photo-dégradation. 2.
Influence de la concentration en catalyseur
sur la cinétique de la réaction.
-
L’évolution de la réaction dépend de
la concentration en dioxyde de titane.
-
Plus la concentration en dioxyde de
titane est grande et plus la courbe décroît rapidement.
-
Plus la concentration en catalyseur
est grande et plus le système évolue rapidement.
-
Pour une concentration de
0,1 g . L–1, la durée de
la réaction est d’environ
4 h (courbe
rouge).
-
Pour une concentration de
0,5 g . L–1, la durée
de la réaction est d’environ
3 h
(courbe bleue) |
3)- Exercice 05 page 85 : Exploiter des informations sur la catalyse :
|
Exploiter des informations sur la catalyse : A.
La découverte de la catalyse. « Le mot catalyse fut créé par BERZELIUS. C’est pourquoi on lui fit l’honneur de cette découverte, alors qu’elle est due à deux français CLÉMENT et DESORMES, son beau-père. C’est en 1806, dans une note à l’Institut de France à propos de la formation de l’acide sulfurique dans une chambre à plomb, que se trouve expliqué pour la première fois le
mécanisme catalytique. » D’après La découverte de la catalyse, P. LEMAY, Dans Courrier médical, 29 mai 1938. B.
La chambre à plomb. Le procédé de la chambre à plomb est le procédé historique de production industrielle de l’acide sulfurique. Introduit par John ROEBUCK en 1746, il met en œuvre une réaction
d’équation : SO2 + ½ O2 +
H2O → H2SO4 La réaction est plus rapide en présence d’oxydes d’azote. Ces
derniers sont continuellement recyclés. D’après Société chimique de France.
-
Extraire deux informations montrant
que les oxydes d’azote agissent en catalyseurs. |
Exploiter des informations sur la catalyse : L’acide sulfurique (huile de vitriol) est essentiellement un
produit de l’industrie. On le trouve dans certains torrents volcaniques de l’Amérique du
Sud. Il est le composant principal des nuages de la planète Vénus. Dans les sols, l’oxydation du soufre est très lente à l’air
humide. Cette réaction est favorisée par la lumière solaire et une
température de 40 ° C. Acide
sulfurique
d
= 1,815
M
= 98
g . mol–1
Pourcentage en masse : 90 %
H290 : Peut être corrosif pour les métaux
H314 : Provoque des brûlures de la peau
et
des lésions oculaires graves L’acide sulfurique est utilisé dans l’industrie chimique,
industrie du pétrole, industrie textile, l’industrie alimentaire, la métallurgie. Il sert à la préparation des engrais, des détergents, d’explosifs
(nitroglycérine, trinitrotoluène TNT),… Actuellement, on utilise le procédé de contact
comme mode de production industrielle de l’acide sulfurique. Comme catalyseur de la réaction, on utilise du pentaoxyde de
vanadium , V2O5.
-
Ce procédé comporte 3 étapes :
-
Étape 1 :
Combustion :
-
Production du dioxyde de soufre SO2,
par combustion du soufre S,
-
Étape 2 :
Conversion :
-
Oxydation du dioxyde de soufre SO2
en trioxyde de soufre, SO3, en présence d’un catalyseur, le pentoxyde de vanadium, V2O5,
-
Étape 3 :
Absorption :
-
Obtention d’acide sulfurique H2SO4,
par réaction sur l’acide dilué du trioxyde de soufre SO3. Le procédé de la chambre de plomb,
fournit un acide sulfurique moins concentré et contenant plus d'impuretés. Il est plutôt destiné à la fabrication
d’engrais (les
superphosphates). L’addition d’eau à l’acide sulfurique produit un dégagement de
chaleur important et provoque des projections d’acide sulfurique. Mis en contact avec la peau, l’acide sulfurique occasionne de
graves brûlures. Il est préférable de verser délicatement l’acide dans l’eau et
non l’inverse.
-
Deux informations montrant que les
oxydes d’azote agissent en catalyseurs
-
La réaction est plus rapide en
présence d’oxydes d’azote.
-
Ces derniers sont continuellement
recyclés.
-
Les oxydes d’azote accélèrent la
réaction chimique.
-
Les oxydes d’azote sont régénérés en
fin de réaction pour être recyclés.
-
Ils n’apparaissent pas dans le bilan
de la réaction.
-
Le catalyseur :
-
Un catalyseur est une espèce chimique
qui accélère une réaction chimique.
-
Au cours de la transformation, il est
consommé puis régénéré.
-
En conséquence, sa formule n’apparaît
pas dans l’équation de la réaction.


![]()
4)- Exercice 06 page 85 : Déterminer un temps de demi-réaction :
|
Déterminer un temps de demi-réaction : On trace l’évolution, en fonction du temps, des concentrations d’un mélange réactionnel en ions fer II Fe2+ (aq) et en ions argent
Ag+ (aq) au cours de la réaction d’équation : 2 Ag+ (aq) + Fe (s) →
Fe2+ (aq) + 2 Ag (s) Le métal fer est en excès. Représentation graphique : 1.
Évaluer la durée tf de la
réaction. 2.
Temps de demi-réaction t1/2
et durée de réaction tf: a.
Déterminer, par deux méthodes différentes,
le temps de demi-réaction, t1/2. b.
Le comparer à la durée de réaction, tf. |
Déterminer un temps de demi-réaction : 1.
Évaluation la durée tf de
la réaction.
-
Exploitation graphique :
-
La durée de la réaction est d’environ
60 min :
-
tf ≈ 60 min 2.
Temps de demi-réaction t1/2
et durée de réaction tf: a.
Détermination, par deux méthodes
différentes, le temps de demi-réaction, t1/2.
-
Le temps de demi-réaction
t1/2 d’un système chimique est la durée au bout de laquelle la moitié du réactif limitant a été
consommé.
-
Réaction chimique : 2 Ag+ (aq) + Fe (s) →
Fe2+ (aq) + 2 Ag (s)
-
Le métal fer est en excès.
-
En conséquence l’ion Ag+
(aq) est le réactif limitant :
-
Or : [Ag+]0
= 0,080 mol . L–1
-
Au bout de la durée t1/2 : [Ag+]t1/2 =
0,040 mol . L–1
-
Exploitation graphique :
-
On peut déterminer
t1/2 à partir de l’évolution de la concentration du produit Fe2+
(aq) au cours du temps :
-
Le temps de demi-réaction
t1/2 est la date pour laquelle :
-
-
Exploitation graphique : b.
Comparaison entre la durée de réaction, tf
et le temps de demi-réaction, t1/2.
-
La réaction est terminée au bout de 6
t1/2 environ :
-
tf ≈ 6
t1/2
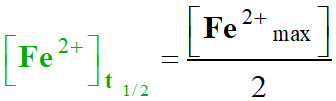
![]()
5)- Exercice 08 page 85 : Déterminer une vitesse d’apparition :
|
Déterminer une vitesse d’apparition : On trace l’évolution temporelle de la concentration en diiode I2 (aq), [I2] = f (t), lors de la réaction entre les ions iodure I–
(aq) et le peroxyde d’hydrogène H2O2
(aq). L’équation de la réaction s’écrit : 2 I– (aq) + H2O2
(aq) + 2 H+ (aq) →
I2 (aq) + H2O (ℓ) - Déterminer graphiquement les vitesse volumiques d’apparition du diiode à
t1 = 0 min
et t2 = 10
min, puis conclure.
|
|
Déterminer une vitesse d’apparition :
-
Détermination graphique des vitesse
volumiques d’apparition du diiode à
t1 = 0 min et
t2 = 10 min :
►
Vitesse volumique d’apparition d’un
produit I2 :
-
La vitesse
vapp (I2)t
d’apparition ,du produit
I2 (aq), est
égale à la dérivée par rapport au temps de sa concentration :
-
►
Détermination graphique - À l’instant t1, la vitesse vapp (I2)t1 est aussi égale au coefficient directeur de la tangente à la courbe [I2] = f (t)
donnant l’évolution de la concentration du produit
I2 en fonction
du temps t.
-
Vitesse volumiques d’apparition du
diiode à t1 =
0 min :
-
Exploitation du graphe :
-
La vitesse
vapp (I2)0 est
aussi égale au coefficient directeur
a0 de la
tangente T0.
-
-
Vitesse volumiques d’apparition du
diiode à t2 =
10 min
-
Exploitation graphique :
-
La vitesse
vapp (I2)10 est
aussi égale au coefficient directeur
a10 de la
tangente T10.
-
-
Conclusion :
-
Au cours de la réaction, la vitesse
d’apparition du diiode au cours du temps diminue.
-
vapp (I2)0
> vapp (I2)10
-
La vitesse volumique d’apparition
d’un réactif diminue au cours du temps.
-
La courbe tend vers une asymptote
horizontale et le coefficient directeur de la tangente à la courbe
tend vers zéro.
-
La vitesse d’une transformation
chimique est maximale à l’instant initial.
-
Elle décroît ensuite et s’annule
lorsque la réaction est terminée.
-
Les réactifs sont consommés au fur et
à mesure que la réaction se poursuit.
-
Comme la concentration des réactifs
est un facteur cinétique, la diminution de la concentration des
réactifs entraîne la diminution de la vitesse.
-
Elle
s’annule si le réactif limitant à totalement disparue. |
6)- Exercice 10 page 86 : Vérifier un ordre de réaction :
|
Vérifier un ordre de réaction : On étudie la décomposition du pentoxyde de diazote N2O5. À température élevée, le pentaoxyde de diazote,
de formule N2O5 se décompose selon la réaction lente suivante : 2 N2O5
(g)
-
Tableau de valeurs :
1. Recopier les données expérimentales dans un tableur, puis calculer la valeur de la vitesse de disparition du
pentaoxyde de diazote aux différentes dates du tableau. 2.
Tracer le graphe de l’évolution de la
vitesse en fonction de la concentration [N2O5]t. 3.
Vérifier que la réaction est d’ordre 1 par
rapport au pentaoxyde de diazote. |
|
Vérifier un ordre de réaction : 1.
Exploitation des données expérimentales avec
le un tableur Excel :
►
Première méthode :
-
On utilise la relation approchée suivante pour
calculer la valeur de la vitesse
de disparition du pentoxyde de
diazote aux différentes dates :
-
-
Ainsi pour
vdisp (N2O5)t0 :
-
-
Calcul avec le tableur :
-
Dans la cellule D6, on tape la
formule suivante :
-
= – (C7 – C6) / (B7 – B6)
-
Puis en recopie cette formule vers le
bas autant que nécessaire.
-
Tableau de valeurs :
-
On trace le graphe :
v (N2O5)
=
f ([N2O5])
-
Les points sont sensiblement alignés.
On peut tracer la droite moyenne qui passe
pratiquement par
l’origine.
-
Étude statistique réalisée avec le
tableur Excel :
-
L’équation de la droite :
-
Elle est du type :
-
y ≈ 0,0325
x
-
Traduction physique :
-
v
(N2O5)
≈ 0,0325 × [N2O5]
-
La vitesse de disparition du
pentoxyde de diazote
v (N2O5)
est proportionnelle
à la concentration en pentoxyde de
diazote [N2O5].
-
En conséquence, la réaction suit la
loi de vitesse d’ordre 1 par rapport au
pentoxyde de diazote
N2O5.
►
Deuxième méthode :
-
On trace le graphe
[N2O5]
=
f (t)
avec le tableur Excel :
-
On obtient la courbe suivante :
-
On réalise une étude statistique avec
le tableur Excel :
-
Comme courbe de tendance, on choisit
« Exponentielle » :
-
On affiche , l’équation de la courbe
et le coefficient de détermination
R2.
-
Le coefficient de détermination est
très proche de 1.
-
Le modèle choisit est bien en accord
avec les données expérimentales.
-
L’adéquation est bonne.
-
Équation de la courbe :
-
[N2O5]
≈250 ×
e–0,035
×
t
-
D’après la définition de la vitesse
de disparition du pentaoxyde de diazote :
-
-
On peut déterminer l’expression de la
dérivée de la vitesse de disparition
du pentaoxyde de diazote :
-
-
La vitesse de disparition du
pentoxyde de diazote
v (N2O5)
est proportionnelle
à la concentration en pentoxyde de
diazote [N2O5].
-
En conséquence, la réaction suit la
loi de vitesse d’ordre 1 par rapport
au pentoxyde de diazote
N2O5. 2.
Graphe de l’évolution de la vitesse en
fonction de la concentration [N2O5]t.
-
Tableau de valeurs :
-
Dans la cellule D6,
-
Formule : = 0,035 * C6
-
On recopie vers le bas autant que
nécessaire :
-
Représentation graphique : 3.
Vérification que la réaction est d’ordre 1
par rapport au pentaoxyde de diazote.
-
v
(N2O5)
≈ 0,035 × [N2O5]
-
La vitesse de disparition du
pentoxyde de diazote
v (N2O5)
est proportionnelle
à la concentration en pentoxyde de
diazote [N2O5].
-
En conséquence, la réaction suit la
loi de vitesse d’ordre 1 par rapport
au pentoxyde de diazote
N2O5. |
7)- Exercice 12 page 86 : Déterminer la valeur d’une dérivée :
|
Déterminer la valeur d’une dérivée : En milieu acide, le peroxyde d’hydrogène H2O2 (aq) réagit avec les ions iodure I–
(aq) selon la réaction d’équation :
H2O2 (aq) + 2
I–
(aq) + 2 H+
(aq)→ I2 (aq) + 2 H2O
(ℓ) On trace :
-
L’évolution de la concentration c
en diiode de la solution en fonction du temps (courbe
rouge) ;
-
La tangente à cette courbe au point
d’abscisse 0 (droite
verte). Représentation graphique : 1.
Déterminer graphiquement la vitesse
d’apparition du diiode à l’instant t = 0 min. 2.
Pour t € [0 ; 7], on modélise la
concentration c par la fonction :
-
-
Exprimer
c’ (t),
puis valider la réponse donnée à la question 1. |
|
Déterminer la valeur d’une dérivée : En milieu acide, le peroxyde d’hydrogène H2O2
(aq) réagit avec les ions iodure I–
(aq) selon la réaction d’équation :
H2O2 (aq) + 2
I– (aq) + 2 H+
(aq) → I2 (aq) + 2 H2O
(ℓ) 1.
Détermination graphique de la vitesse
d’apparition du diiode à l’instant t = 0 min.
►
Détermination graphique - À l’instant t1, la vitesse vapp (I2)t1 est aussi égale au coefficient directeur de la tangente à la courbe [I2] = f (t)
donnant l’évolution de la concentration du produit I2
en fonction du temps t.
-
Vitesse d’apparition du diiode à
l’instant t = 0 min
-
Il faut déterminer la valeur du
coefficient directeur de la
droite verte.
-
2.
Pour t € [0 ; 7], on modélise la
concentration c par la fonction :
-
-
Expression de
c’
(t) :
-
-
Vitesse d’apparition du diiode à
l’instant t = 0 min
-
-
Unité : mmol . L–1 . min–1 - On retrouve le résultat de la question 1.
Additif :
-
On peut tracer sur un même
graphique : c =
f (t) et
c’ =
g (t).
-
Représentation graphique :
-
Étude de la courbe
c’ (t) (courbe
bleue) :
-
Pour t € [0 ; 3,3], la valeur de la
vitesse vapp (I2)t
augmente :
-
Elle est maximale pour
t ≈ 3,3 min et vmax
≈ 0,87 mmol . L–1 . min–1
-
Pour t € [3,3 ; 7], la valeur de la
vitesse vapp (I2)t
diminue.
-
Étude de la courbe
c (t) (courbe
rouge) :
-
Cette courbe présente un point
d’inflexion.
-
En ce point la dérivée seconde de
c (t)
s’annule :
-
-
Date à laquelle la dérivée seconde
s’annule.
-
-
Pour cette valeur, la vitesse
vapp (I2)t est extrémale.
-
Cette réaction
"semble" être catalysée par un
des produits de la réaction.
-
On dit qu’elle est autocatalysée.
-
Une réaction est autocatalysée
lorsque l’un des produits de la réaction est un catalyseur de cette réaction.
-
Remarque :
-
En toute rigueur, le terme
autocatalyse est un terme impropre car le catalyseur apparaît dans le bilan de la réaction.
-
Lors d’une autocatalyse, deux
facteurs agissent en sens inverse sur la cinétique de la réaction :
-
L’augmentation de la concentration du
produit catalyseur qui accélère la réaction.
-
La diminution de la concentration des
réactifs qui ralentit la réaction.
-
Au début, la réaction s’accélère car
l’effet catalytique est important et il y a beaucoup de réactifs.
-
Puis la vitesse diminue à cause de la
diminution de la concentration des réactifs.
|
8)- Exercice 14 page 87 : Modélisation d’une courbe :
|
Modélisation d’une courbe : On étudie la réaction entre les ions peroxodisulfate S2O82–
(aq) et les ions iodure I– (aq). L’équation de la réaction s’écrit : S2O82–
(aq) + 2 I– (aq) → SO42–
(aq) + I2 (aq) La seule espèce colorée est le diiode I2 (aq). Des mesures d’absorbance du mélange réactionnel en fonction du
temps ont permis d’obtenir les résultats suivants :
1.
Déterminer les valeurs des concentrations [I2]t
du I2 (aq) aux différentes dates du tableau. 2.
Établir la relation entre [S2O82–]t
et [S2O82–]0
et [I2]t. 3.
À l’aide d’un tableur, tracer l’évolution de
la concentration [S2O82–]t
en ions peroxodisulfate S2O82– (aq)
en fonction du temps. 4.
Modéliser le graphe obtenu par une
fonction : f (t) = [S2O82–]0
× exp (– k × t) 5.
En utilisant la modélisation mathématique,
vérifier que la réaction est d’ordre 1 par rapport aux ions
peroxodisulfate.
-
Données :
-
Concentration initiale en ions
peroxodisulfate :
-
[S2O82–]0
= 2,34 × 10–3 mol . L–1
-
Coefficient d’absorption molaire du
diiode dans les conditions de l’expérience :
-
ε = 1190 L . mol–1.
cm–1
-
longueur de la cuve :
-
ℓ = 1,0 cm. |
Modélisation d’une courbe : L’équation de la réaction s’écrit : S2O82–
(aq) + 2 I– (aq) → SO42–
(aq) + I2 (aq) La seule espèce colorée est le diiode I2 (aq). 1.
Détermination des valeurs des concentrations
[I2]t du I2 (aq) aux
différentes dates du tableau.
-
Pour ce faire, il faut utiliser la
loi de Beer-Lambert : L’absorbance d’une
solution diluée contenant une espèce colorée
est proportionnelle à la concentration (effective)
C de cette espèce et
à l’épaisseur ℓ (cm) de la solution traversée par
le faisceau lumineux.
A =
ε .
ℓ . C
A :
absorbance : grandeur sans unité
ℓ :
largeur de la cuve (épaisseur de la solution traversée)
(cm)
ε
(λ) : coefficient d’extinction molaire (mol– 1. L. cm–
1)
C :
concentration de l’espèce absorbante (mol . L– 1)
-
Dans le cas présent :
-
A = ε . ℓ . [I2]t
-
A = 1190 ×
1,0 . [I2]t
-
A
= 1190 ×[I2]t
-
Tableau de valeurs : t
(min)
A [I2] (mmol . L–1) 0,0 0,000 0,000 1,0 0,100 0,084 2,0 0,200 0,168 3,0 0,290 0,244 4,0 0,349 0,293 5,0 0,460 0,387 6,0 0,540 0,454 7,0 0,618 0,519 8,0 0,670 0,563 9,0 0,760 0,639 10,0 0,825 0,693 11,0 0,890 0,748 12,0 0,940 0,790 13,0 1,001 0,841 14,0 1,061 0,892 15,0 1,113 0,935 16,0 1,178 0,990 17,0 1,210 1,017 18,0 1,256 1,055 19,0 1,300 1,092 20,0 1,341 1,127 2.
Relation entre [S2O82–]t
et [S2O82–]0
et [I2]t.
-
Tableau d’avancement : Équation
S2O82– (aq)
+ 2 I– (aq)
→
2 SO42– (aq)
+ I2 (aq)
État
du
système
Avancement
n
(S2O82–)
n
(I–)
n
(SO42–)
n
(I2)
État
initial
(mol)
x =
0
n
(S2O82–)0
n
(I–)0
0,0
0,0
Au
cours
de la
transformation au temps t
x
n
(S2O82–)0
- x
n
(I–)0
– 2 x
2
x
x
État
final
(mol)
x = xmax
n
(S2O82–)0
– xmax
n
(I–)0
–
2
xmax
2
xmax
xmax
-
Au temps
t :
-
n (S2O82–)t =
n (S2O82–)0
– x
-
n (I2) =
x
-
n (S2O82–)t =
n (S2O82–)0
– n (I2)
-
En fonction des concentrations, on
obtient la relation suivante :
-
[S2O82–]t
= [S2O82–]0 – [I2]t
-
[S2O82–]t
= 2,34 × 10–3 – [I2]t
-
Tableau de valeurs : t
(min)
A [I2]
(mmol . L–1) [S2O82–]t
(mmol . L–1) 0,0 0,000 0,000 2,340 1,0 0,100 0,084 2,256 2,0 0,200 0,168 2,172 3,0 0,290 0,244 2,096 4,0 0,349 0,293 2,047 5,0 0,460 0,387 1,953 6,0 0,540 0,454 1,886 7,0 0,618 0,519 1,821 8,0 0,349 0,293 2,047 9,0 0,760 0,639 1,701 10,0 0,825 0,693 1,647 11,0 0,890 0,748 1,592 12,0 0,940 0,790 1,550 13,0 1,001 0,841 1,499 14,0 1,061 0,892 1,448 15,0 0,698 0,587 1,753 16,0 1,178 0,990 1,350 17,0 1,210 1,017 1,323 18,0 1,256 1,055 1,285 19,0 1,300 1,092 1,248 20,0 1,341 1,127 1,213
-
Graphe [S2O82–]t
= f (t) : 4.
Modélisation du graphe obtenu par une
fonction : f (t) = [S2O82–]0
× exp (– k × t)
-
Analyse statistique réalisée avec le
tableur Excel :
-
On sélectionne le graphique, puis
« ajouter courbe de tendance »
-
Comme option de courbe de tendance,
on sélectionne : « exponentielle »
-
Puis, on demande d’afficher
l’équation de la courbe et le coefficient de détermination
R2.
-
On obtient le graphe suivant :
-
Traduction physique :
-
[S2O82–]t
≈ 2,31 × exp (- 0,033
t)
-
R2
≈ 0,9985 ≈ 1
-
Le modèle choisi est bien en accord avec
les mesures expérimentales. 5.
Réaction d’ordre 1 par rapport aux ions
peroxodisulfate. Une réaction chimique est d’ordre 1 par rapport au
réactif
A,
si
lorsque le réactif B est en large excès,
les vitesses volumiques de disparition des réactifs
ou
d’apparition des produits sont proportionnelles à la
concentration [A]t
de l’espèce A au cours du temps :
Ainsi, on peut écrire :
-
-
La vitesse de disparition du
peroxodisulfate S2O82– est proportionnelle à la concentration en
ions peroxodisulfate [S2O82–].
-
La réaction est d’ordre 1 par rapport
aux ions peroxodisulfate S2O82–.
-
Représentation graphique de [S2O82–] =
f (t) et [I2] = g (t) Ou
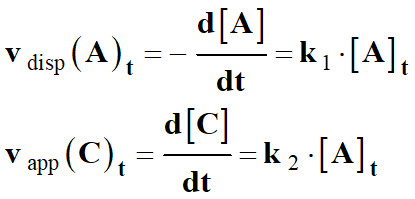
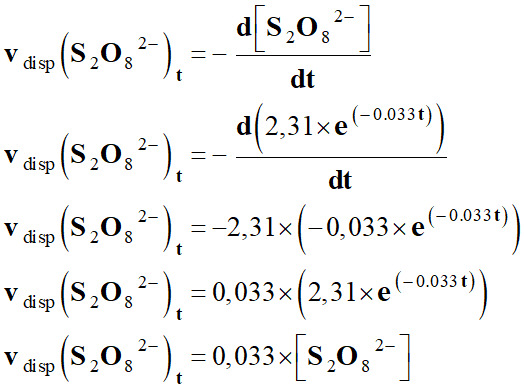
![]()
9)- Exercice 15 page 87 : L’eau de Javel :
|
L’eau de Javel : Une étiquette d’eau de Javel porte, entre autres, les
recommandations suivantes :
Les propriétés désinfectantes de l’eau de Javel sont dues aux
ions hypochlorite CℓO– (aq). La concentration d’une eau de Javel est définie par le degré
chlorométrique (° Chℓ) :
-
Plus
de degré chlorométrique est élevé, plus la concentration en ions
hypochlorite est grande. Au cours du temps, la quantité d’ions hypochlorite diminue. Le graphique suivant représente l’évolution du degré
chlorométrique en fonction du temps : 1.
Exploitation du graphique : a.
Pour chacune des courbes, déterminer
graphiquement les vitesses de disparition des ions hypochlorite à t
= 4 semaines. b.
Quel facteur cinétique est mis en évidence ? c.
La recommandation « à conserver au frais »
est-elle justifiée ? 2.
Vitesses de disparition : a.
Pour chacune des courbes, déterminer
graphiquement les vitesses de disparition des ions hypochlorite à t
= 12 semaines. b.
Interpréter l’évolution de la vitesse au
cours du temps. 3.
Proposer une hypothèse permettant
d’expliquer la recommandation « à conserver à l’abri de la lumière ».
|
L’eau de Javel : 1.
Exploitation du graphique : a.
Les vitesses de disparition des ions
hypochlorite à t = 4 semaines.
-
À l’instant
t1, la vitesse
vdisp (CℓO–)t1 est
aussi égale à l’opposé du coefficient directeur
de la tangente à la
courbe [I2] = f (t)
donnant l’évolution de la concentration du réactif
CℓO– (aq) en
fonction du temps t.
-
Courbe
C20 :
-
-
Courbe
C30 :
-
-
Courbe
C40 :
-
b.
Facteur cinétique est mis en évidence :
-
La courbe donnée représente les
variations du degré chlorométrique en fonction du temps.
-
La réaction qui se produit est la
suivante : 2 ClO– (aq)
→
O2 (g)
+ 2
Cl– (aq)
-
Le degré chlorométrique est lié à la
concentration en ion hypochlorite ClO– (aq).
-
Plus de degré chlorométrique est
élevé, plus la concentration en ions hypochlorite est grande
-
En conséquence, on remarque que la
concentration en ion hypochlorite diminue au cours du temps.
-
On s’aperçoit que pour une même durée
(exemple : t1 = 8 semaines), la concentration en
ion hypochlorite est d’autant plus petite que la température est
élevée.
-
C1 > C2
> C3.
-
Le facteur cinétique mis en évidence
est la température. c.
La recommandation « à conserver au frais »
est-elle justifiée ?
-
La recommandation est justifiée car
plus la température est élevée, plus la concentration en ion
hypochlorite (agent actif de l’eau de Javel) diminue rapidement. 2.
Vitesses de disparition : a.
Les vitesses de disparition des ions
hypochlorite à t = 12 semaines.
-
Courbe
C20 :
-
-
Courbe
C30 :
-
-
Courbe
C40 :
-
-
Récapitulatif : Température
Vitesses (° Chℓ . semaine–1)
T ° C
4
semaines
8
semaines
20
1,3
0,92
30
2,5
1,0
40
2,6
0,46
-
Pour une même température, la valeur
de la vitesse de disparition de l’ion hypochlorite décroît au cours
du temps.
-
Elle décroît d’autant plus vite que
la température est élevée.
-
La vitesse volumique d’apparition
d’un réactif ou de disparition d’un produit diminue au cours du
temps. -
Les courbes [P] = f (t)
et [R] = g (t)
tendent vers une asymptote horizontale et le coefficient
directeur de la tangente à la courbe tend vers zéro.
-
La vitesse d’une transformation
chimique est maximale à l’instant initial.
-
Elle décroît ensuite et s’annule
lorsque la réaction est terminée.
-
Les réactifs sont consommés au fur et
à mesure que la réaction se poursuit.
-
Comme la concentration des réactifs
est un facteur cinétique, la diminution de la concentration des
réactifs entraîne la diminution de la vitesse.
-
Elle
s’annule si le réactif limitant à totalement disparue. 3.
Proposer une hypothèse permettant
d’expliquer la recommandation « à conserver à l’abri de la
lumière ».
-
Pour accélérer certaines réactions,
on peut utiliser l’énergie lumineuse.
-
L’éclairement d’un milieu réactionnel
avec une radiation de longueur d’onde appropriée peut accélérer une
réaction chimique.
-
Les récipients opaques permettent
d’éviter que la réaction soit accélérée par la présence de
radiations UV.
-
L’eau de Javel est commercialisée
dans des récipients opaques.
-
La recommandation : « À conserver
à l’abri de la lumière » est accord avec cette observation.
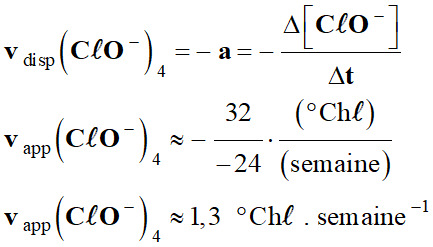
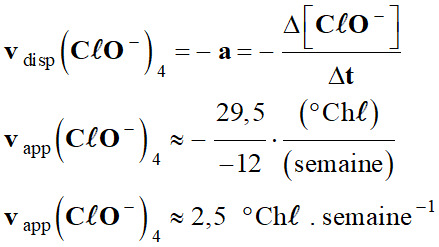
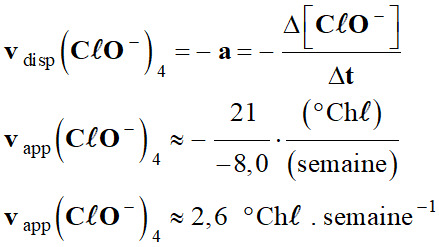
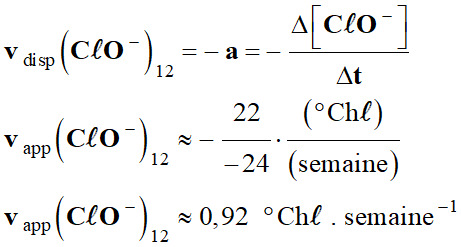
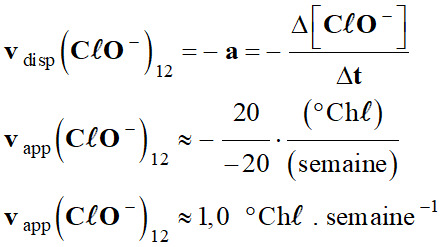
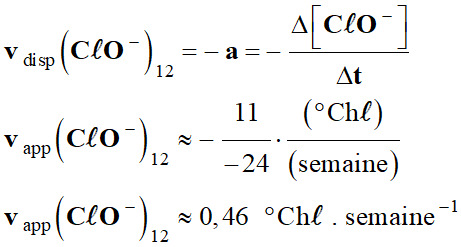
![]()
10)- Exercice 19 page 87 : Analyse médicale :
|
Analyse médicale : Les phosphatases alcalines (PAL) sont des enzymes présentes dans le sang et éliminées par la bile, liquide sécrétée par le foie. En cas de
maladie du foie, un bilan hépatique peut être prescrit par un médecin pour évaluer la
concentration en PAL dans le sang. Lors de l’analyse, on étudie l’hydrolyse basique du paranitrophénylphosphate (noté PNPP). En présence des enzymes PAL, la vitesse de disparition du PNPP est augmentée. Le paranitrophénolate (noté PNP) issu de
cette hydrolyse basique est la seule espèce colorée.
La réaction a pour équation : PNPP + HO– → PNP +
HPO42– Ou On réalise une hydrolyse du PNPP avec une concentration
initiale en PNPP égale à : [PNPP]0 = 1,0 × 10–5 mol . L–1. On mesure l’évolution de l’absorbance A au cours du temps
t. La courbe obtenue est donnée ci-dessous : 1.
Justifier l’utilisation d’un
spectrophotomètre pour suivre l’évolution de la concentration en PNP de
la solution. 2.
Pourquoi l’étude de l’absorbance du PNP
au cours du temps permet-elle d’accéder à la concentration en
PNPP dans le sang.
-
On donne A = k × [PNP]
avec k = 1,85 × 104 L . mol–1. 3.
La catalyse : a.
Qu’est-ce qu’un catalyseur ? b.
Qu’est-ce qui permet d’affirmer que l’enzyme
PAL est un catalyseur de la réaction ? c.
Comment nomme-t-on ce type de catalyse ? 4.
Étude de la vitesse : a.
Exploiter la courbe en déduire la vitesse
d’apparition du PNP, à t = 0 et à t = 50 min. b.
Comment la vitesse évolue-t-elle au cours du
temps ? Pour quelle raison ? 5.
Définir le temps de demi-réaction et
l’évaluer graphiquement. 6.
Pourquoi les résultats de l’analyse ne
peuvent-ils pas être obtenus immédiatement ? 7.
Montrer de manière simple que cette réaction
est d’ordre 1 par rapport au PNPP.
|
|
Analyse médicale :
1.
Utilisation d’un spectrophotomètre pour
suivre l’évolution de la concentration en PNP de la solution.
-
La réaction a pour équation :
hydrolyse basique PNPP + HO– → PNP +
HPO42–
-
Le paranitrophénolate (noté
PNP) issu de cette hydrolyse basique est la seule espèce colorée. - Pour réaliser les mesures d’absorbance, le spectrophotomètre est généralement réglé sur la
longueur d’onde
λmax correspondant au maximum d’absorption du spectre de la
solution étudiée. 2.
Absorbance du PNP et concentration en
PNPP dans le sang.
-
Pour les solutions
suffisamment diluées, l’absorbance
A est proportionnelle à la concentration
C de l’espèce colorée (Loi de Beer-Lambert)
-
On donne A = k × [PNP]
avec k = 1,85 × 104 L . mol–1.
-
Connaissant la valeur de l’absorbance
A du
PNP, on peut en déduire la valeur de la concentration en [PNP] :
-
-
Tableau d’avancement : PNPP + HO– → PNP +
HPO42–
-
Au temps
t, pour l’avancement
x, on écrit les relations
suivantes :
-
n (PNPP)t =
n (PNPP)0
– x et n (PNP) t = x
-
n (PNPP)t =
n (PNPP)0
– n (PNP)t
-
Cette relation est valable pour les
concentrations des différentes espèces chimiques.
-
Elles sont présentes dans le même
volume V de solution
(milieu réactionnel) :
-
[PNPP]t =
[PNPP]0
– [PNP]t
-
À partir de l’absorbance de l’espèce
colorée PNP, on peut en
déduire la concentration [PNPP].
-
Relation :
-
3.
La catalyse : a.
Le catalyseur :
-
Un catalyseur est une espèce chimique
qui accélère une réaction chimique.
-
Au cours de la transformation, il est
consommé puis régénéré.
-
En conséquence, sa formule n’apparaît
pas dans l’équation de la réaction. b.
L’enzyme PAL est un catalyseur de la
réaction :
-
L’enzyme PAL est un catalyseur
car il augmente la vitesse de la réaction d’hydrolyse basique du
paranitrophénylphosphate (noté
PNPP).
-
Il n’apparaît pas dans le bilan de la réaction.
-
Au cours de la réaction, il est
consommé, puis régénéré en fin de réaction.
-
Type de catalyse : catalyse
enzymatique 4.
Étude de la vitesse : a.
Vitesse d’apparition du PNP, à t
= 0 et à t = 50 min. - La vitesse vapp (PNP) est aussi égale au coefficient directeur a de la tangente T à la courbe
[PNPP]
= f (t) à l’instant considéré.
-
-
On peut connaître la valeur du
coefficient directeur de la tangente en passant par la courbe
A = f (t) :
-
Or
-
-
Vitesse d’apparition du
PNP, à t = 0 :
-
-
De même pour t = 50 min :
-
-
On détermine la valeur de grâce
-
Application
numérique :
-
-
b.
Évolution de la vitesse au cours du temps :
-
On remarque que
vapp (PNP)50
< vapp (PNP)0
-
La vitesse d’apparition de
PNP diminue au cours du temps car la concentration des réactifs
diminue au cours de l’avancement de la réaction. 5.
Temps de demi-réaction
-
Définition : -
Le temps de demi-réaction
t1/2 d’un système chimique est la durée au bout de laquelle la moitié du réactif limitant a été consommée.
-
Dans le cas présent :
-
On peut déterminer
t1/2 à partir de l’évolution de la concentration d’un
produit P au cours du
temps :
-
Le temps de demi-réaction
t1/2 est la date pour laquelle :
-
-
Comme
-
-
Le temps de demi-réaction est la date
pour laquelle :
-
-
Évaluation graphique :
-
t1/2 ≈ 23 min. 6.
Les résultats de l’analyse et la durée :
-
Pour avoir les résultats de
l’analyse, il faut attendre la fin de la réaction d’hydrolyse
basique du paranitrophénylphosphate (noté
PNPP).
-
Il faut attendre environ 7
t1/2 ≈ 23 min ≈ 2,7 h. 7.
Réaction est d’ordre 1 par rapport au
PNPP.
On utilise le fait que :
-
On remarque que :
-
Entre
0
et
1
t1/2, la concentration de l’espèce
PNP a augmenté de [PNP]max
/ 21.
-
Entre
1
t1/2 et
2
t1/2, la
concentration de l’espèce
PNP a augmenté de [PNP]max
/ 22.
-
Entre
2
t1/2 et
3
t1/2, la
concentration de l’espèce
PNP a augmenté de [PNP]max
/ 23.
-
Ceci est caractéristique d’une
réaction qui suit une loi de vitesse d’ordre 1 par rapport au réactif PNPP. - Car [PNPP]t = [PNPP]0 – [PNP]t
-
Et
-
On peut tracer le graphe
[PNPP]t =
f (t)
-
On remarque que, au bout du temps :
-
1
t1/2, la
concentration de l’espèce
[PNPP] a été
divisée par 21.
-
2
t1/2, la
concentration de l’espèce
[PNPP] a été
divisée par 22.
-
3
t1/2, la
concentration de l’espèce
[PNPP] a été
divisée par 23.
-
n
t1/2, la
concentration de l’espèce
[PNPP] a été
divisée par 2n.
-
Ceci est caractéristique d’une
réaction qui suit une loi de vitesse d’ordre 1 par rapport au
réactif PNPP.
|
||||||||||||||||||||||||||||||||||||||
|
|