I- Les facteurs cinétiques.

1)- Introduction.

-  L’étude de l’évolution temporelle de systèmes chimiques constitue la cinétique chimique.

-  Certains paramètres agissent sur la rapidité d’évolution d’un système chimique.

-  Ces paramètres sont appelés : les facteurs cinétiques de la réaction.

►  Classification cinétique :

-  À l’échelle humaine, on distingue trois catégories de transformations chimiques :

2)- Influence de la température.

a)-  Oxydation des ions iodure par de peroxyde d’hydrogène en milieu acide.

►  Expérience :

  A l’instant t = 0, 0 s,

-  Remarque :

-  Le peroxyde d’oxygène H₂O₂ (aq) (eau oxygénée) est l’oxydant du couple :

-  H₂O₂ (aq) / H₂O (ℓ)

-  Observations :

-  Au cours du temps, la solution contenue dans le bécher prend une teinte brun-orangé de plus en plus intense.

DS première 

-  On peut observer l’évolution de la transformation grâce au changement de teinte de la solution.

-  Le changement de teinte est dû à la formation de diiode en milieu aqueux (pour simplifier).

-  Autre couple qui intervient : I₂ (aq) / I^– (aq)

- L'ion iodure I^– (aq) est le réducteur du couple I₂ (aq) / I^– (aq)

►  Interprétation.

-  Il se produit une réaction d’oxydoréduction entre les ions iodure et l’eau oxygénée en milieu acide.

-  Cette transformation est lente par rapport à l’échelle humaine. On peut suivre son évolution.

  Écrire l’équation de la réaction chimique.

b)-  Mise en évidence du rôle de la température des réactifs :

►  Expérience 1 : Oxydation des ions iodure par de peroxyde d’hydrogène en milieu acide.

-  On observe l’évolution de la coloration de la solution au cours du temps à différentes températures.

-  Tableau :

►  Conclusion.

-  La température d’un mélange réactionnel est un facteur cinétique.

-  L’avancement temporel d’une réaction augmente généralement avec la température.

-  La vitesse de formation ou de disparition d'un corps augmente généralement avec la température.

c)-  Utilisation de ce facteur cinétique.

►  Accélération et déclenchement d’une réaction chimique.

-  Certaines réactions, trop lentes à température ambiante, sont réalisées à température plus élevée, ainsi elles deviennent plus rapides.

-  Pour accélérer la cuisson des aliments, on utilise des autocuiseurs.

-  En augmentant la température, on diminue le temps de cuisson des aliments.

-  Les mélanges comburant-combustible sont en général cinétiquement inertes à température ambiante :

-  Pour initier la réaction, on utilise une allumette ou une étincelle entre les deux électrodes d’une bougie de moteur.

-  C’est le point chaud qui déclenche la combustion.

►  Ralentissement ou arrêt d’une réaction chimique.

-  La trempe :

-  Elle désigne le refroidissement brutal d’un milieu réactionnel pour le rendre cinétiquement inerte.

-  On utilise ce procédé lors de dosages en séances de travaux pratiques pour arrêter la réaction à un instant donné t.

-  Si le refroidissement est assez rapide, le système n’évolue plus et conserve la composition qu’il avait juste avant le refroidissement.

-  D’autre part, pour ralentir les réactions indésirables, on place les aliments au réfrigérateur ou au congélateur.

3)- Influence de la concentration des réactifs.

a)-  Expérience 2 : Dismutation de l’ion thiosulfate en milieu acide.

  Dans un bécher de 100 mL, on verse :

-  45 mL de thiosulfate de sodium de concentration C₁ = 0,13 mol / L,

-  5 mL de solution d’acide chlorhydrique de concentration C₂ = 0,10 mol / L.

-  on observe la formation d’un précipité qui trouble peu à peu la solution.

-  La transformation est lente, on peut observer son évolution.

►  Interprétation :

-   Le précipité obtenu est un précipité jaune de soufre.

-  Couples mis en jeu : S₂O₃^2– (aq) / S (s) et  SO₂ (aq) / S₂O₃^2– (aq) 

   Écrire l’équation de la réaction de dismutation.

-  On dit que l’ion thiosulfate se dismute car il apparaît dans deux couples différents en tant que réducteur dans un couple et oxydant dans l’autre couple.

-   La réaction de dismutation de l’ion thiosulfate en milieu acide est une transformation lente.

b)-  Influence de la concentration des réactifs.

►  Principe :

-  On utilise la réaction précédente.

-  En milieu acide, l’ion thiosulfate réagit lentement avec les ions hydrogène et donne un précipité de soufre qui reste en suspension.

-  La solution devient peu à peu opaque. On utilise ce phénomène pour évaluer la vitesse moyenne de formation de soufre.

-  On place, avant le début de l’expérience, sous le bécher, une feuille de papier portant une croix à l’encre noire.

-  On déclenche le chronomètre au moment où l’on mélange la solution de thiosulfate de sodium et l’acide chlorhydrique.

-  On note la durée nécessaire Δt pour que la croix ne soit plus visible.

-  Pour que l’épaisseur à travers laquelle on observe la croix soit toujours la même, on utilise des béchers identiques et des volumes de solutions identiques.

-  On admet que la quantité de matière n_d de soufre nécessaire à la disparition du motif est la même dans toutes les expériences.

  Influence de la concentration de la solution en ions thiosulfate.

-  Dans un bécher de 100 mL, on verse :

-  45 mL de thiosulfate de sodium de concentration C₁.

-  5 mL de solution d’acide chlorhydrique de concentration C₂ = 0,10 mol / L.

-  tableau :

  Influence de la concentration de la solution d’acide chlorhydrique.

-  Dans un bécher de 100 mL, on verse :

-  45 mL de thiosulfate de sodium de concentration C₁ = 0,13 mol / L,

-  5 mL de solution d’acide chlorhydrique de concentration C₂ .

-  tableau :

►  Conclusion :

-  De façon générale,

-  L’évolution d’un système chimique est d’autant plus rapide que les concentrations des réactifs sont élevées.

4)- La catalyse.

a)-  Définition.

b)-  Expérience : La dismutation de l’eau oxygénée

►  Étude de la solution d’eau oxygénée.

  Eau oxygénée à 20 volumes :

-  Le peroxyde d’hydrogène présent dans l’eau oxygénée n’est pas stable.

-  Il est impliqué dans deux couples oxydant / réducteur :

-  Couple 1 : H₂O₂ (aq) / H₂O (ℓ)

-  Couple 2 : O₂ (g) / H₂O₂ (aq)

-  On peut envisager une réaction entre H₂O_{2 (aq)} , oxydant du couple 1 et H₂O_{2 (aq)} , réducteur du couple 2 :

-  Cette réaction est appelée réaction de dismutation.

-  La transformation associée est spontanée mais très lente à la température ordinaire.

-  Cette réaction est très lente.

-  Si l’on verse de l’eau oxygénée dans un bécher, il n’est pas possible d’observer un dégagement de dioxygène.

►  Étude de la solution d’eau oxygénée en présence, d’ions fer II, ions fer III et de platine.

  Bécher A : eau oxygénée seule.

  Bécher B : eau oxygénée + solution aqueuse de sulfate de fer II

  Bécher C : eau oxygénée + solution de chlorure de fer III

  Bécher D : eau oxygénée + fil de platine

►  Observations :

-  Dans le bécher A, pas d’évolution visible.

-  Dans les autres béchers, on observe un dégagement intense de dioxygène.

On observe un dégagement gazeux de dioxygène

Apparition de bulles de dioxygène à la surface du fil de platine

ZOOM

►  Conclusion

-  Les ions fer II, les ions fer III et le platine accélèrent la réaction de dismutation du peroxyde d’hydrogène.

-  Ce sont des catalyseurs de la réaction de dismutation du peroxyde d’hydrogène.

►  La dismutation de l’eau oxygénée en présence d’ions fer III.

-  Grâce à la présence du catalyseur, on remplace une étape lente par deux étapes rapides.

-  Étape 1 : réaction entre l’eau oxygénée est les ions fer III. Réaction rapide :

-   étape 2 : réaction entre l’eau oxygénée et les ions fer II. Réaction rapide 

-   Bilan global de la réaction : Il faut combiner (1) et (2).

-  Le catalyseur d’apparaît pas dans le bilan de la réaction.

c)-  Caractéristiques d’un catalyseur.

-  Un catalyseur est une espèce chimique qui accélère une réaction chimique.

-  La formule du catalyseur n’apparaît pas dans l’équation de la réaction.

-  Un catalyseur modifie la nature des étapes permettant de passer des réactifs aux produits.

-  La réaction globale lente est remplacée par plusieurs réactions rapides.

►  Catalyse homogène :

-  La catalyse est dite homogène lorsque le catalyseur et le mélange réactionnel constituent une seule phase (forment un mélange homogène).

-  C’est le cas des gaz et des liquides miscibles.

-  Exemples : dismutation de l’eau oxygénée en présence d’ions fer II ou d’ions fer III.

►  Catalyse hétérogène :

-  La catalyse est dite hétérogène lorsque le catalyseur et le milieu réactionnel se trouvent dans des phases différentes.

-  Exemples :

-  Expérience de la lampe sans flamme (on utilise un fil de cuivre chauffé comme catalyseur)

-  Dismutation de l’eau oxygénée catalysée par un fil de platine.

►  Catalyse enzymatique :

-  La catalyse est enzymatique lorsque le catalyseur est une enzyme.

-  Les enzymes sont des catalyseurs biologiques qui permettent aux transformations chimiques nécessaires à la vie de s’effectuer à vitesse élevée.

-  Les enzymes sont des protéines.

-  Le nom d’une enzyme indique souvent la transformation mise en jeu :

-  L’amylase transforme l’amidon en maltose.

-  La saccharase catalyse l’hydrolyse du saccharose en glucose et fructose.

-  Les réductases catalysent les réductions des groupes carbonyles, acides et esters.

-  Les enzymes sont très utilisées dans l’industrie agroalimentaire :

-  Fabrication du pain, préparation de boissons fermentées, conservation des aliments, …

-  Exemple : l’hydrolyse de l’amidon au laboratoire : il faut travailler à température élevée et en milieu fortement acide.

5)- Autres facteurs cinétiques.

►  L’éclairement :

-  Pour accélérer certaines réactions, on peut utiliser l’énergie lumineuse.

-  L’éclairement d’un milieu réactionnel avec une radiation de longueur d’onde appropriée peut accélérer une réaction chimique.

-  Exemple : la synthèse chlorophyllienne

-  Les végétaux, grâce à leur chlorophylle et grâce à l’énergie solaire transforment le dioxyde de carbone CO₂ atmosphérique en molécules organiques, le glucose :

-  E = h . υ

-  C’est la synthèse chlorophyllienne.

►  Le solvant :

-  Le solvant peut être un facteur cinétique.

-  Ainsi, certaines réactions chimiques sont plus rapides dans l’eau que dans l’éthanol.

-  Exemple :

II- La vitesse d’évolution d’un système.

1)- Vitesses volumiques.

a)-  Introduction :

-  Considérons la réaction naturelle suivante :

a . A  +  b . B  →  c . C  +  d . D

-  A et B sont les réactifs,  C et D sont les produits et a, b, c et d sont les coefficients stœchiométriques.

-  Pour connaître l'évolution d'une réaction chimique, il suffit de connaître à chaque instant la quantité de matière présente de l'une des espèces chimiques.

-  Exemple : Considérons la réaction chimique suivante.

-  Au temps t = 0 s

-  Il se produit la réaction suivante :

-  Tableau d’avancement :

-  x est lié à « l’avancement de la réaction » :

-  x ≤ n₁ et 2 x ≤ n₂

-  Si par dosage, on détermine la quantité de matière x en diiode au temps t, on peut en déduire les quantités de matière des autres espèces présentes dans le milieu réactionnel.

-  Si le mélange réactionnel a un volume constant V au cours de la réaction, on peut dans ce cas suivre l'évolution de la réaction en travaillant avec les concentrations.

-  Au cours de la réaction, les produits se forment et les réactifs disparaissent.

►  Vitesse d’apparition d’un produit ou de disparition d’un réactif :

-  On suit l'évolution de la quantité de matière d'un produit au cours du temps : n_p = f (t).

-  Ou on suit l’évolution de la quantité de matière d’un réactif au cours du temps : : n_R = g (t)

►  Vitesse moyenne d’apparition d'un produit P.

►  Vitesse moyenne de disparition d'un réactif R.

►  Vitesse d'apparition d'un produit P.

-  La vitesse va(P) d’apparition du produit P à la date t1 est,   par définition, la limite de la vitesse moyenne d'apparition   de ce même produit entre t1 et t2 quand t2 tend vers t1. -  On écrit : -    -  Cette limite est égale à  la valeur prise par la dérivée de la   fonction np = f (t) au temps t1. -  On écrit : -  -  Graphiquement : cette vitesse est numériquement égale à la   valeur du coefficient directeur de la tangente T à la courbe   np = f (t) au point M1 d'abscisse t1.

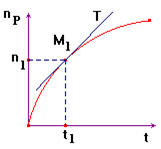►  Vitesse de disparition d'un réactif R.

- Si le mélange réactionnel a un volume constant V au cours de la réaction, on peut dans ce cas suivre l'évolution de la réaction en travaillant avec les concentrations :

- Dans le cas d’un produit de la réaction :

-  n_P = [P] . V avec V =cte.

-   

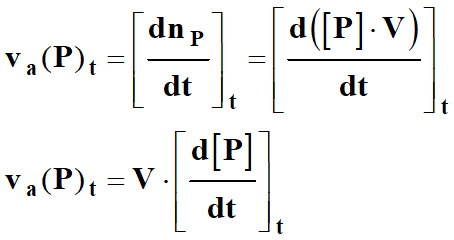
-  On définit alors la vitesse volumique d’apparition du produit P en faisant intervenir la concentration :

-   

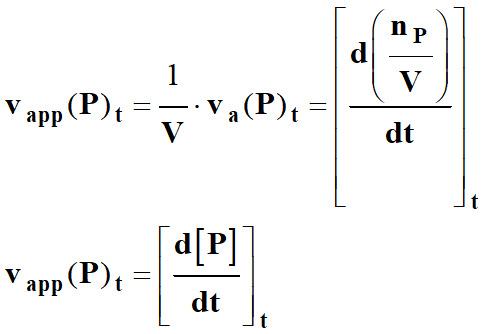
-  Dans ce cas l’unité de vitesse volumique : mol .L^–1 . min^–1

b)-  Définitions.

►  Vitesse volumique d’apparition d’un produit P :

-  La vitesse volumique d’apparition v_app (P)_ti d’un produit P à l’instant t_i est assimilée au taux de variation de sa concentration [P] entre les instants proches t_i et t_i+1 :

-   

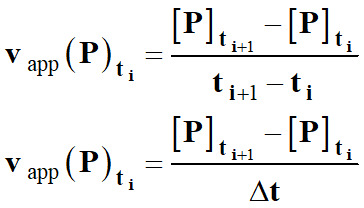
-  Lorsque l’on fait tendre Δt → 0,

-  Le taux de variation de la concentration [P] tend vers le nombre dérivé de [P] à l’instant considéré.

►  Vitesse volumique d’apparition d’un produit P :

►  Remarque :

-  À l’instant t₁, la vitesse v_app (P)_t1 est aussi égale au coefficient directeur de la tangente à la courbe [P] = f (t) donnant l’évolution de la concentration du produit P en fonction du temps t.

-  Représentation graphique :

-  On peut aussi définir la vitesse de disparition d’un réactif dans un volume constant.

-  Comme on veut que cette grandeur soit positive, on la définit comme l’opposé du taux de variation de la concentration [R].

►  Vitesse volumique de disparition d’un réactif R :

-  La vitesse volumique de disparition v_disp (R)_ti d’un réactif R à l’instant t_i est assimilée à l’opposé du taux de variation de sa concentration [R] entre les instants proches t_i et t_i+1 :

-   

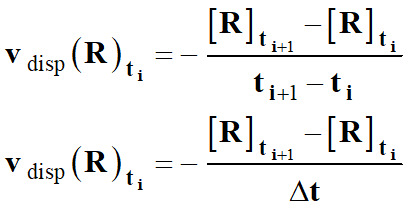
-  Lorsque l’on fait tendre Δt → 0,

-  Le taux de variation de la concentration [R] tend vers l’opposé du nombre dérivé de [R] à l’instant considéré.

►  Vitesse volumique de disparition d’un réactif R :

►  Remarque :

-  À l’instant t₁, la vitesse v_disp (R)_t1 est aussi égale à l’opposé du coefficient directeur de la tangente à la courbe [R] = f (t) donnant l’évolution de la concentration du réactif R en fonction du temps t.

-  Représentation graphique :

►  Vitesse volumique et unités :

-  La vitesse volumique peut s’exprimer en mol . L^–1 . s^–1

-  On peut utiliser aussi : mol . L^–1 . min^–1

2)- Temps de demi-réaction.

-  À la date t = 0, la concentration initiale du réactif A est [A]₀.

-  Le temps de demi-réaction t_1/2 est la date pour laquelle :

-   

-  Détermination graphique :

►  Remarque 1 :

-  Le temps de demi-réaction t_1/2  dépend en général de la concentration initiale du réactif A.

-  Le temps de demi-réaction t_1/2 n'est pas caractéristique de la substance A.

-  Le temps de demi-réaction t_1/2 permet d’évaluer la durée nécessaire à l’achèvement de la transformation chimique étudiée.

►  Remarque 2 :

-  On peut déterminer t_1/2 à partir de l’évolution de la concentration d’un produit P au cours du temps :

-  Le temps de demi-réaction t_1/2 est la date pour laquelle :

-   

-  Détermination graphique :

3)- Méthode de suivi cinétique.

-  Le suivi cinétique d’une réaction consiste à déterminer expérimentalement la relation existant entre la quantité de matière (ou la concentration) d’un réactif R ou d’un produit P et le temps t.

-  Le but est la détermination expérimentale de : n_R = f ( t) ou [R] = g (t).

-  Pour ce faire :

-  On peut mesurer une grandeur physique comme :

-  l’absorbance, la conductivité, la pression ou le volume,…

-  grâce à un capteur.

-  On peut réaliser des titrages successifs de l’une des espèces, en prélevant toujours le même volume du mélange réactionnel à différentes dates.

-  Dans ce cas :

-  On prélève un échantillon de volume V du mélange réactionnel ;

-  On réalise la trempe avec dilution à différentes dates t, pour stopper la réaction ;

-  On détermine la concentration d’une espèce chimique présente par titrage.

III- Loi de vitesse d’ordre 1.

1)- Définition.

-  Considérons la réaction chimique suivante :

a A + b B → c C + d D

►  Exemple : La dismutation de l’eau oxygénée :

-  Équation de la réaction :

-  Cette réaction est d’ordre 1 par rapport au peroxyde d’hydrogène.

-  On peut donc écrire :

-  Cas d’un réactif R :

-   

-  Cas d’un produit P :

- 

-  Remarque :  k₁ et k₂ sont des constantes positives.

2)- Reconnaître une loi de vitesse d’ordre 1.

-  Considérons la réaction chimique suivante :

a A + b B → c C + d D

-  Lorsque le réactif B est en large excès, il existe plusieurs méthodes pour vérifier que cette réaction est d’ordre 1 par rapport au réactif A :

►  Méthode 1 :

-  Il faut vérifier que le temps de demi-réaction t_1/2 est indépendant de la concentration initiale [A]₀ de l’espèce A.

►  Méthode 2 :

-  Il faut vérifier que les vitesses volumiques de disparition des réactifs ou d’apparition des produits sont proportionnelles à la  concentration [A]_t de l’espèce A au cours du temps.

►  Méthode 3 :

-  Il faut vérifier que l’évolution de la concentration [A]_t de l’espèce A au cours du temps obéit à une loi exponentielle du type :

-  [A]_t = [A]₀ . exp (- k . t)

-  [A]_t = [A]₀ . e ^{- k . t}

►  La fonction exponentielle :

-  C’est la fonction f (x), notée e^x telle que :

-  f (0) = 1 et f’ (x) = f (x)

-  C’est la fonction réciproque de la fonction logarithme népérien, notée ln x,

-  Relation : ln (e^x) = x

-  Représentation graphique de e^x :

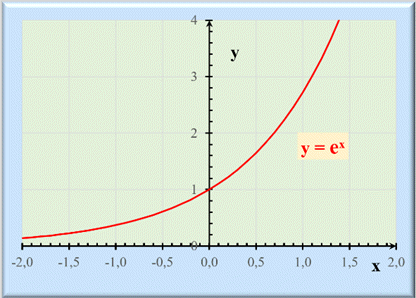
►  Remarques :

-  Influence de la concentration initiale [A]₀ de l’espèce A :

-  [A₁]₀ > [A₂]₀  > [A₃]₀

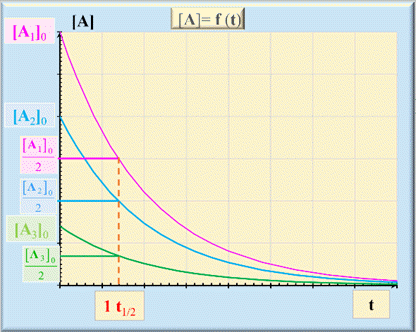
-  On remarque que le temps de demi-réaction t_1/2 est le même.

►  Autre caractéristique du temps de demi-réaction t_1/2 :

-  Représentation graphique de [A]_t = f (t)

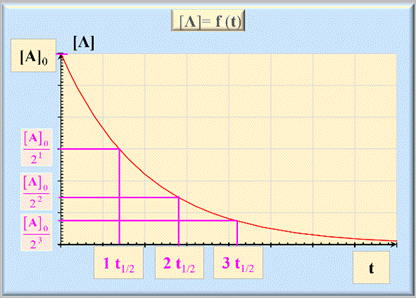
-  On remarque que, au bout du temps :

-  1 t_1/2, la concentration de l’espèce A a été divisée par 2¹.

-  2 t_1/2, la concentration de l’espèce A a été divisée par 2².

-  3 t_1/2, la concentration de l’espèce A a été divisée par 2³.

-  n t_1/2, la concentration de l’espèce A a été divisée par 2ⁿ.

-  Ceci est caractéristique d’une réaction qui suit une loi de vitesse d’ordre 1 par rapport au réactif A.

-  Cas d’un produit :

-  Représentation graphique de [P]_t = g (t)

-  On remarque que  :

-  Entre 0 et 1 t_1/2, la concentration de l’espèce P a augmenté de [P]_max / 2¹.

-  Entre 1 t_1/2 et 2 t_1/2, la concentration de l’espèce P a augmenté de [P]_max / 2².

-  Entre 2 t_1/2 et 3 t_1/2, la concentration de l’espèce P a augmenté de [P]_max / 2³.

-  Ceci est caractéristique d’une réaction qui suit une loi de vitesse d’ordre 1 par rapport au produit  P.

►  Conclusion :

3)- Évolution de la vitesse volumique au cours du temps.

-  La vitesse volumique d’apparition d’un réactif ou de disparition d’un produit diminue au cours du temps.

-  Exemple de graphe :

-  Les courbes [P] = f (t) et [R] = g (t)  tendent vers une asymptote horizontale et le coefficient directeur de la tangente à la courbe tend vers zéro.

-  La vitesse d’une transformation chimique est maximale à l’instant initial.

-  Elle décroît ensuite et s’annule lorsque la réaction est terminée.

-  Les réactifs sont consommés au fur et à mesure que la réaction se poursuit.

-  Comme la concentration des réactifs est un facteur cinétique, la diminution de la concentration des réactifs entraîne la diminution de la vitesse.

-  Elle s’annule si le réactif limitant à totalement disparue.

4)- Pour aller plus loin :

-  Soit la réaction suivante :

a A + b B → c C + d D

-  On considère que la réaction chimique est d’ordre 1 par rapport au réactif A et que le réactif B est en large excès.

- En conséquence, on peut écrire la relation suivante pour le réactif A :

-   

- La grandeur k représente la constante de la vitesse.

-  On en déduit la relation :

-  [A]_t = [A]₀ . exp (- k . t)

-  ou 

-  [A]_t = [A]₀ . e ^{- k . t}

-  On peut utiliser la relation liant à la fonction logarithme népérien et la fonction exponentielle :

-  La fonction exponentielle est la fonction inverse de la fonction logarithme népérien :

-  e⁰ = 1 et ln (e^x) = x

-  ln ([A]_t = [A]₀ . e ^{- k . t}) = ln ([A]₀) + ln (e ^{- k . t})

-  ln ([A]_t = ln ([A]₀) – k . t

-  La fonction ln ([A]) = f (t)  est une fonction affine du type :

-  f (ln ([A]) = a . t + b

-  La grandeur a, coefficient directeur la droite obtenue, représente l’opposée de la constante de la vitesse k.

-  k = – a

-  La grandeur b , ordonnée à l’origine, représente le logarithme népérien de la valeur de la concentration de l’espèce A à l’instant initial.

-  [A]₀ = b

-  Exploitation d’une représentation graphique :

►    Exemple : ln (C) = f (t)

- Tableau de valeurs :

-  Exploitation de la courbe : ln (C) = f (t) :

-  Détermination de la valeur de la constante de la vitesse k :

-   

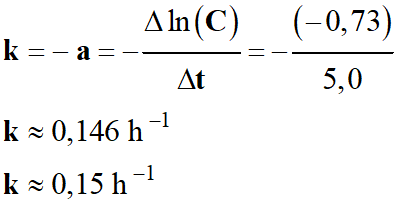
-  Détermination de la valeur de la concentration initiale C₀ :

-  ln (C₀) = b ≈ 4,61

-  C₀ (mmol . L^–1) = exp (b) ≈ exp (4,61)

-  C₀ (mmol . L^–1) ≈ 1,00 × 10²

-  Cette valeur est bien en accord avec celle donnée dans le tableau.

-  Temps de demi-réaction :

-  On peut écrire la relation suivante :

-   

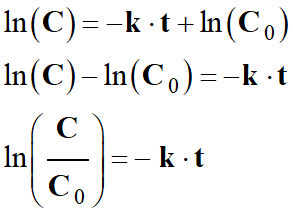
- À la date t = 0, la concentration initiale du réactif est C₀.

-  Le temps de demi-réaction t_1/2 est la date pour laquelle :

-   

-   

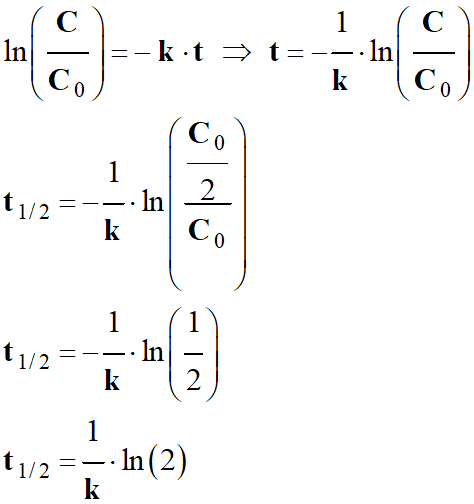
- Application numérique :

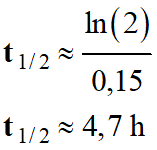-   (ceci en gardant en mémoire les résultats intermédiaires)

-  Relation à retenir :

-  Pour une réaction d’ordre 1 par rapport au réactif A :

-   

-   

IV- Applications.

1)- Suivi cinétique d’une réaction chimique (Expoitation avec Latis-Pro).

Suivi cinétique d'une réaction chimique

2)- QCM.

3)- Exercices.

Exercices :   Préparation à l’ECE :  Étude d’un solvant : l’éthanoate d’éthyle   DS 1)- Exercice 02 page 84 : Justifier une méthode expérimentale. 2)- Exercice 04 page 84 : Étudier l’influence d’un catalyseur. 3)- Exercice 05 page 85 : Exploiter des informations sur la catalyse. 4)- Exercice 06 page 85 : Déterminer un temps de demi-réaction. 5)- Exercice 08 page 85 : Déterminer une vitesse d’apparition. 6)- Exercice 10 page 86 :  Vérifier un ordre de réaction. 7)- Exercice 12 page 86 : Déterminer la valeur d’une dérivée. 8)- Exercice 14 page 87 : Modélisation d’une courbe. 9)- Exercice 15 page 87 : L’eau de Javel. 10)- Exercice 19 page 87 : Analyse médicale. 11)- DS N° 01 : Le parfum de poire (30 min)  : exercice 22 page 90. 12)- DS N° 02 : Ordre d’une réaction (30 min) : Exercice 23 page 87. 13)- DS N° 03 : Vitesse d’une réaction (30 min) : Exercice 24 page 91.