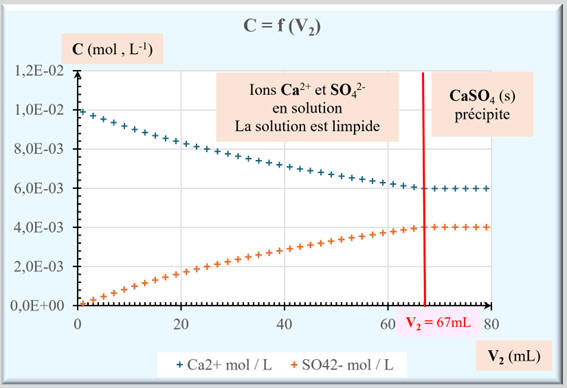
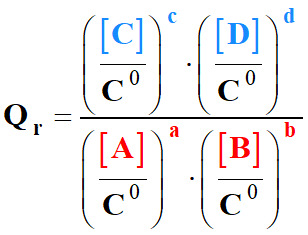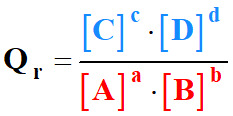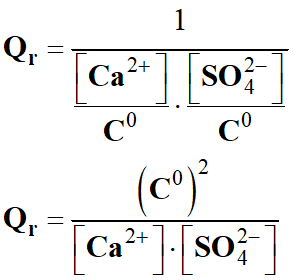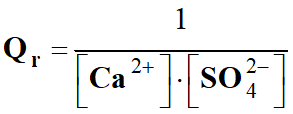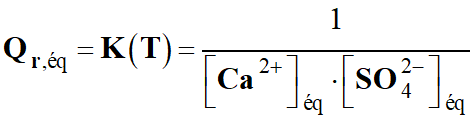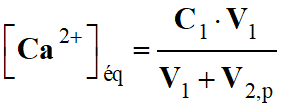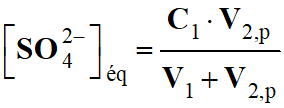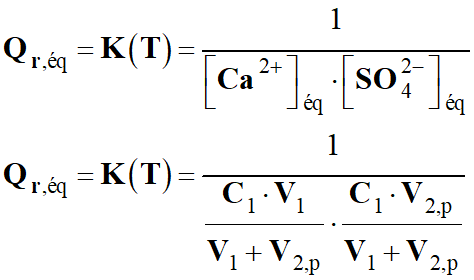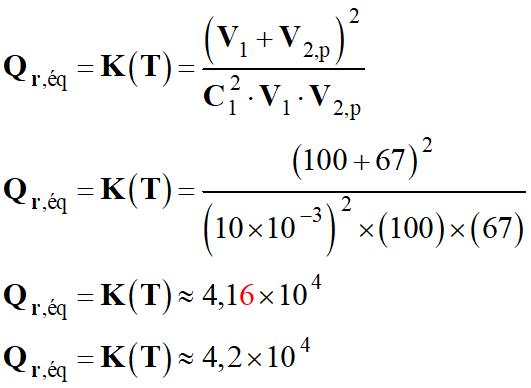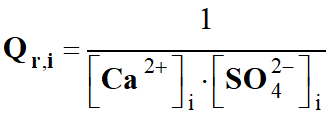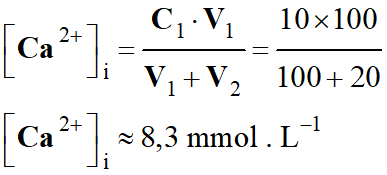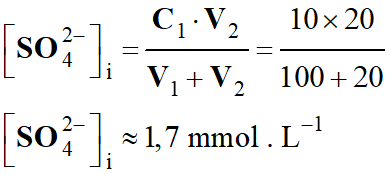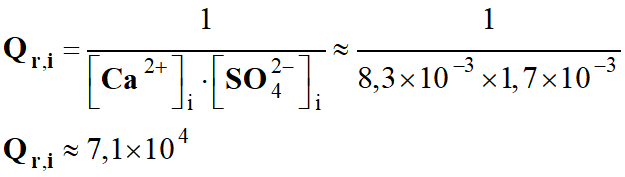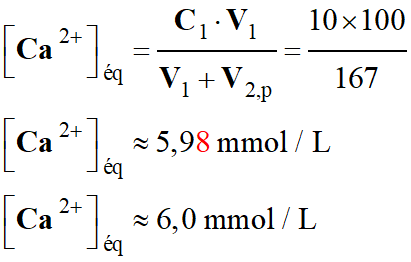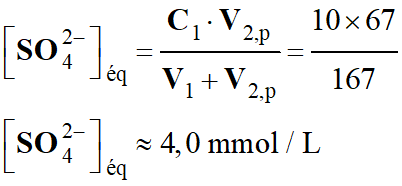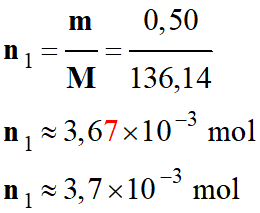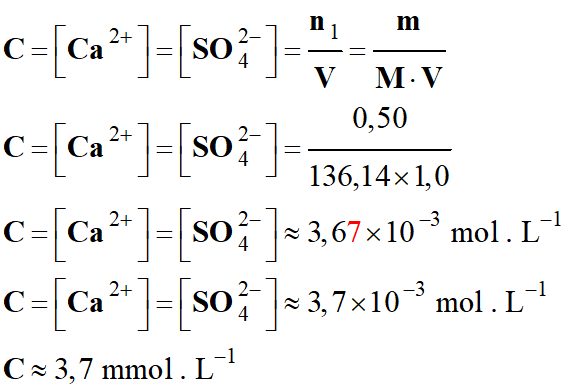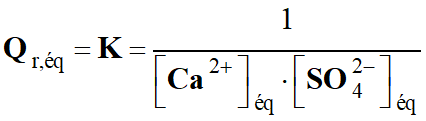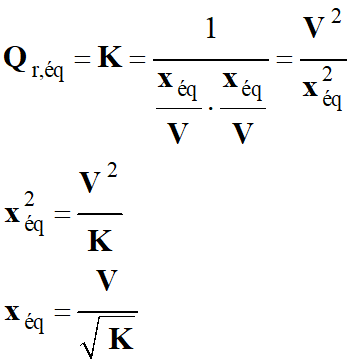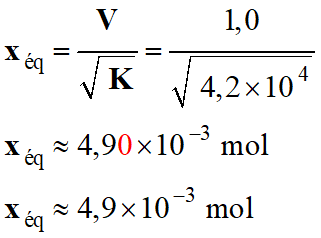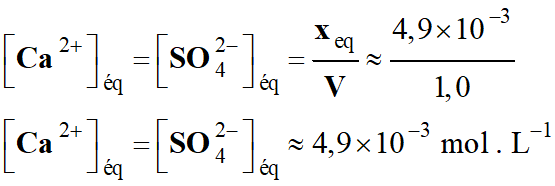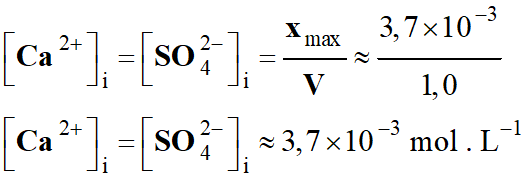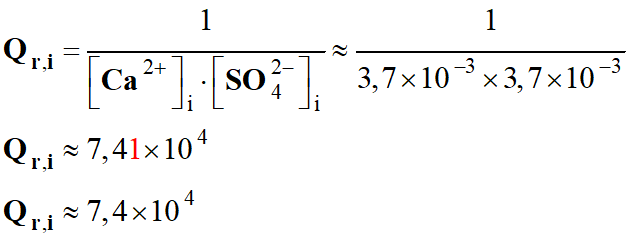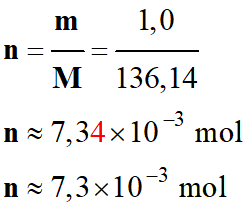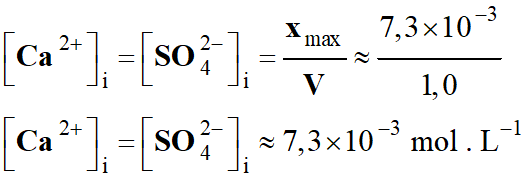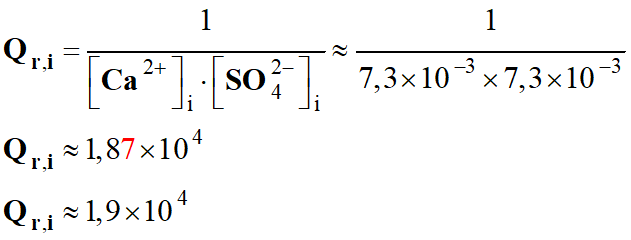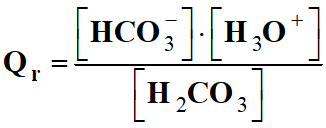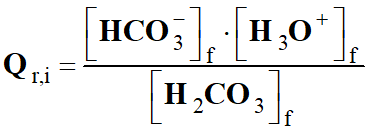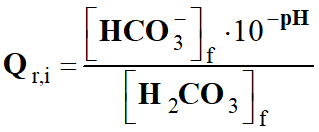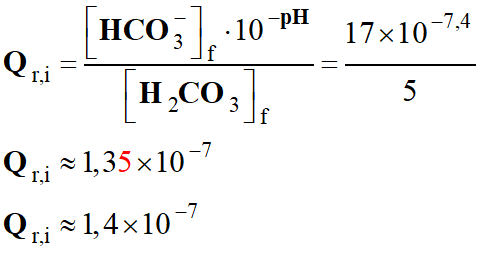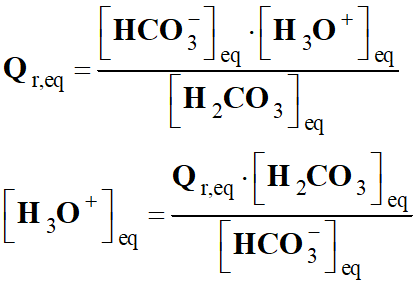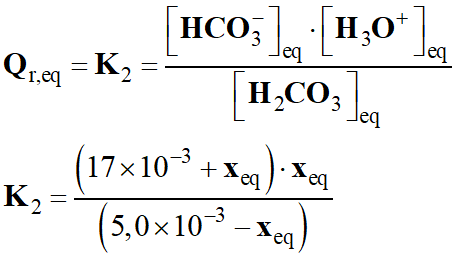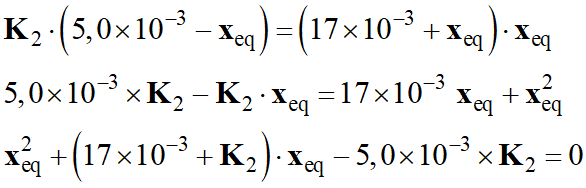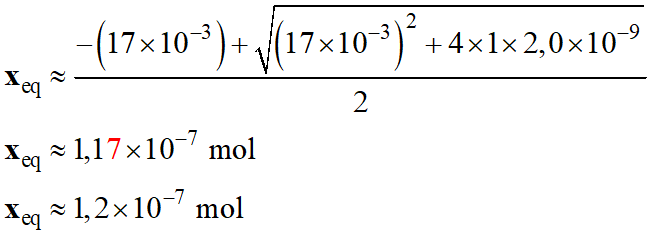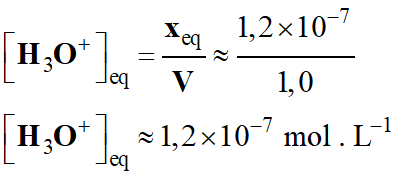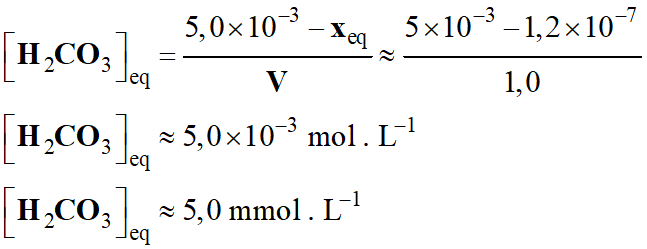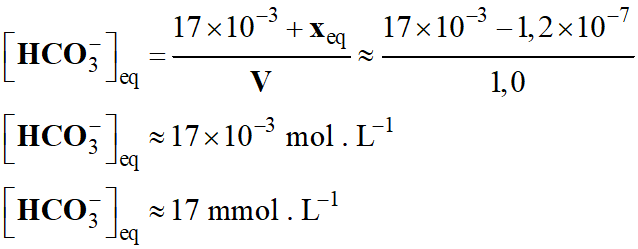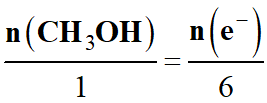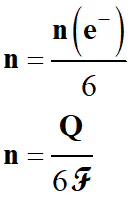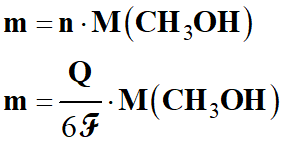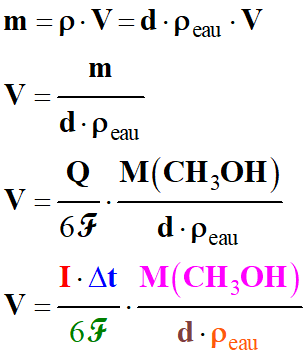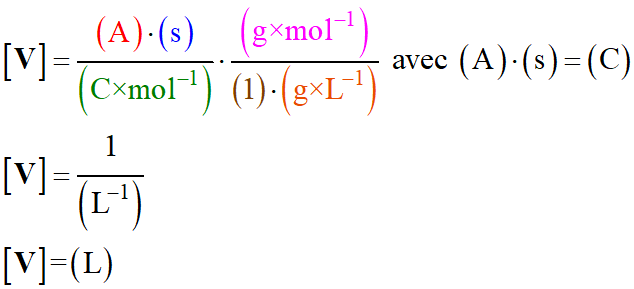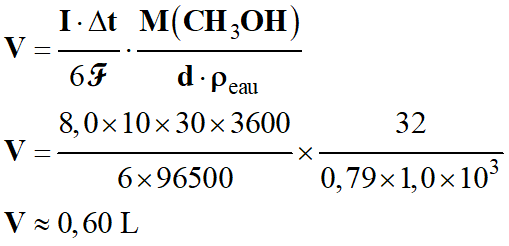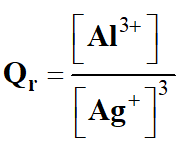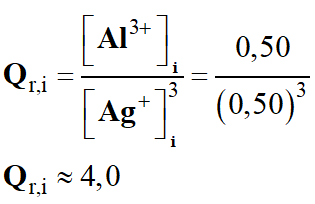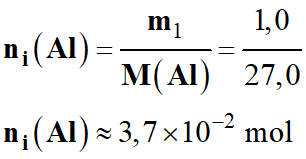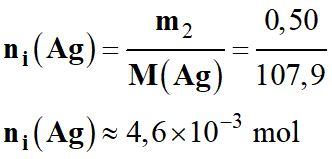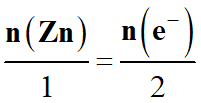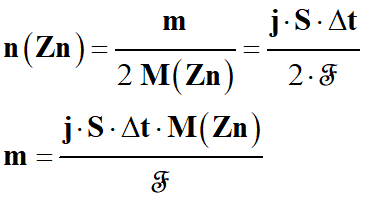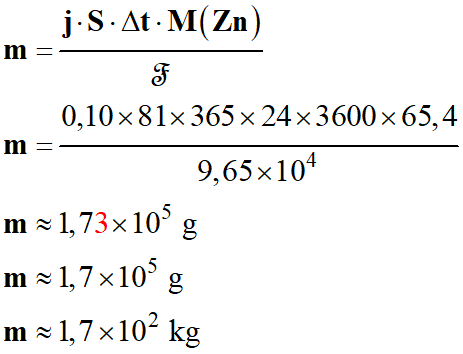1)-
Énoncé.
L'acide lactique CH3
– CH(OH) – CO2H présent dans
l'organisme est issu de la dégradation du glucose en l’absence de dioxygène
(dégradation anaérobie).
La concentration en quantité d'acide lactique dans
le sang est comprise entre 0,50 et 2,2 mmol . L–1.
Le sang peut être assimilé à une solution aqueuse
de pH constant et proche de 7,4.
Le pH du sang maintenu constant grâce à la
présence d'acide carbonique H2CO3 issu
de la solubilisation du dioxyde de carbone et de l’ion hydrogénocarbonate
HCO3–.
À la suite d’un effort musculaire trop intense, des
crampes apparaissent en raison d'une diminution locale du pH sanguin,
conséquence d'une surproduction d'acide lactique.
Dans le sang, l’acide lactique, noté AH,
réagit avec l’ion hydrogénocarbonate HCO3–
suivant la réaction d’équation :
AH (aq) + HCO3–
(aq) → A– (aq) + H2CO3
(aq) (1)
Le dioxyde de carbone dissous formé réagir avec
l'eau présente dans le sang suivant la réaction d'équation :
H2CO3 (aq) + H2O
(ℓ)
 HCO3–
(aq) + H3O+ (aq)
(2)
HCO3–
(aq) + H3O+ (aq)
(2)
La constante d'équilibre à 25 °C de cette réaction
vaut : K2 (T) = 4,0 × 10–7
Avant un effort soutenu, les concentrations en
quantité l'acide carbonique et d’ion hydrogénocarbonate sont :
-
[
H2CO3]i
= 2,0 mmol . L–1 ; [H2CO3–]i
= 20 mmol . L–1
Juste après cet effort, la concentration en
quantité d'acide lactique dans le sang atteint [AH]f = 3,0
mmol . L–1.
a)-
Calculer les concentrations en quantité de [H2CO3]f
et [H2CO3–]f
dans le sang après l'effort.
b)-
Dans le cas de la transformation
(2),
exprimer puis calculer le quotient de réaction
Qr,i à l'état initial
après l'effort et la réaction.
c)-
Déterminer le sens d'évolution du système étudié.
d)-
Calculer la valeur du pH
du sang à l'état final d'équilibre. Commenter ce résultat.

2)- Correction.
a)-
Concentrations en quantité de [H2CO3]f
et [H2CO3–]f
dans le sang après l'effort.
-
Toute la suite ne tient pas
compte de la réaction
(2).
-
On calcule la valeur des
différentes concentrations dans le sang juste après l’effort.
-
[H2CO3]i
= 2,0 mmol . L–1 ; [H2CO3–]i
= 20 mmol . L–1
-
[AH]f
= 3,0 mmol . L–1.
AH
(aq) + HCO3–
(aq) → A– (aq) + H2CO3
(aq) (1)
-
Tableau d’avancement :
|
Équation
|
AH
(aq)
|
+ HCO3–
(aq)
|
→
|
A–
(aq)
|
+
H2CO3 (aq)
|
|
état
|
Avancement
x
(mmol)
|
n
(AH)
|
n
(HCO3–)
|
|
n
(A–)
|
n
(H2CO3)
|
|
État
initial
(mol)
|
0
|
n1
|
n2
|
|
0
|
n3
|
|
Au cours
de la
transformation
|
x
|
n1
– x
|
n2
– x
|
x
|
n3
+ x
|
|
Avancement
final
|
xf
|
n1
– xf
|
n2
– xf
|
xf
|
n3
+ xf
|
|
Avancement
maximal
|
xmax
|
n1
– xmax
|
n2
– xmax
|
|
xmax
|
n3
+ xmax
|
-
Les différentes grandeurs :
-
Quantité de matière initiale
d’acide lactique :
-
Après l’effort : [AH]f
= 3,0 mmol . L–1
-
n1
= [AH]f .
V
-
L’acide lactique réagit avec
l’ion hydrogénocarbonate :
-
Quantité de matière initiale
d’ions hydrogénocarbonate :
-
n2
= [H2CO3–]i.
V avec
[H2CO3–]i
= 20 mmol . L–1
-
Quantité de matière initiale
d’acide carbonique :
-
n3
= [H2CO3]i.
V avec
[H2CO3]i
= 2,0 mmol . L–1
-
L’acide lactique est le
réactif limitant.
-
Tableau d’avancement :
|
Équation
|
AH
(aq)
|
+ HCO3–
(aq)
|
→
|
A–
(aq)
|
+
H2CO3 (aq)
|
|
état
|
Avancement
x
(mmol)
|
n
(AH)
|
n
(HCO3–)
|
|
n
(A–)
|
n
(H2CO3)
|
|
État
initial
(mol)
|
0
|
n1
|
n2
|
|
0
|
n3
|
|
Au cours
de la
transformation
|
x
|
n1
– x
|
n2
– x
|
x
|
n3
+ x
|
|
Avancement
final
|
xf
|
n1
– xf = 0
|
n2
– xf
|
xf
|
n3
+ xf
|
|
Avancement
maximal
|
xmax
|
n1
– xmax
|
n2
– xmax
|
|
xmax
|
n3
+ xmax
|
-
En fin de réaction : la
réaction (1) est une réaction totale.
-
On peut en déduire que :
-
xf
= n1 = [AH]f
. V
-
Quantité de matière d’ion
hydrogénocarbonate après l’effort :
-
n (HCO3–)f
= [HCO3–]i
. V –
xf
-
n (HCO3–)f
= [HCO3–]i
. V – [AH]f
. V
-
[HCO3–]f
. V = [HCO3–]i
. V – [AH]f
. V
-
[HCO3–]f
=
[HCO3–]i
– [AH]f
-
[HCO3–]f
=
20 – 3,0
-
[HCO3–]f
≈
17 mmol . L–1
-
Quantité de matière d’acide
carbonique après l’effort :
-
n (H2CO3)f
= [H2CO3]i
. V +
xf
-
n (H2CO3)f
= [H2CO3]i
. V + [AH]f
. V
-
[H2CO3]f
. V = [H2CO3]i
. V + [AH]f
. V
-
[H2CO3]f
=
[H2CO3]i
+ [AH]f
-
[H2CO3]f
=
2,0 + 3,0
-
[H2CO3]f
≈
5,0 mmol . L–1
b)-
Quotient de réaction Qr,i
à l'état initial après l'effort et la réaction.
-
Bien sûr, à partir du moment
où l’acide carbonique se forme, la transformation
(2)
se produit.
-
Dans le cas de la
transformation
(2) :
H2CO3 (aq) + H2O
(ℓ)
 HCO3–
(aq) + H3O+ (aq)
(2)
HCO3–
(aq) + H3O+ (aq)
(2)
-
K2
(T) = 4,0 × 10–7
-
Expression du quotient de
réaction :
-
L’eau, étant le solvant,
n’intervient pas dans le quotient de la réaction :
-
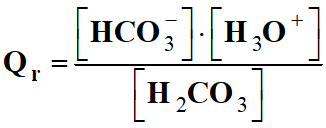
-
Expression du quotient de
réaction initial :
-
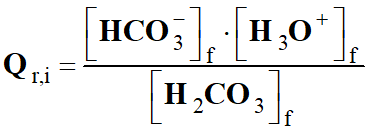
-
Par définition : [H3O+]
= 10–pH
mol . L–1
-
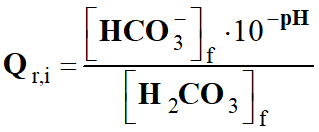
-
Application numérique :
-
Ne pas oublier que le quotient
de réaction est une grandeur qui n’a pas d’unité.
-
Dans le cas présent, il faut
exprimer les concentrations dans la même unité.
-
Le sang peut être assimilé à
une solution aqueuse de pH constant et proche de 7,4 :
-
On prend : pH = 7,4
-
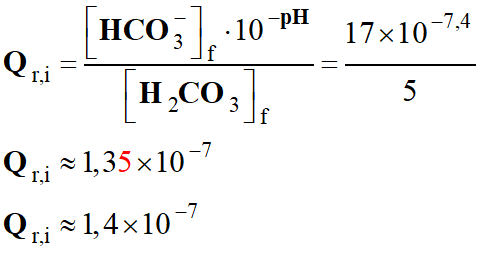
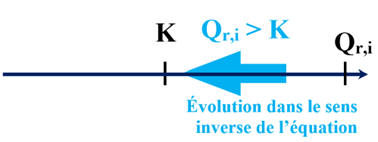
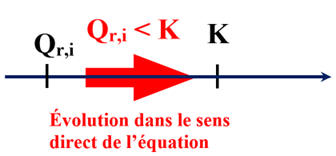
c)-
Sens d'évolution du système étudié :
-
Dans le cas de la
transformation
(2) :
H2CO3 (aq) + H2O
(ℓ)
 HCO3–
(aq) + H3O+ (aq)
(2)
HCO3–
(aq) + H3O+ (aq)
(2)
-
K2
(T) = 4,0 × 10–7
-
Or la valeur du quotient de
réaction initial :
-
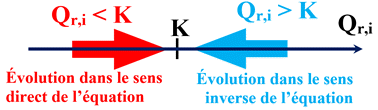
Qr,i ≈ 1,4 × 10–7
-
En conséquence :
-
Qr,i < K2 (T)
|
|
Sens direct
K
|
|
|
H2CO3
(aq) + H2O (ℓ)
|
→
|
HCO3–
(aq) + H3O+ (aq)
|
|
|
Sens inverse
1 / K
|
|
d)-
Valeur du pH du sang à
l'état final d'équilibre.
-
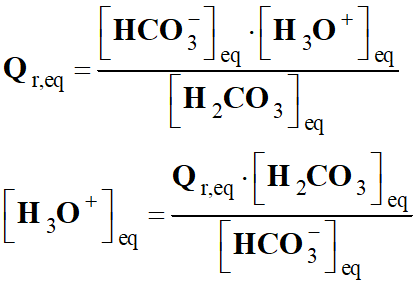
-
Par définition :
pH = – log ([H3O+])
-
-
Avant la réaction
(2) :
-
[HCO3–]f
≈
17 mmol . L–1 et [H2CO3]f
≈ 5,0 mmol . L–1
-
[H3O+]f
= 10– 7,4 mol . L–1
-
[H3O+]f
≈ 4,0 × 10– 8 mol . L–1
-
Quantités de matière pour 1,0
L :
-
n
(HCO3–)f
≈ 17 × 10– 3 mol
-
n
(H2CO3)f
≈ 5,0 × 10– 3 mol
-
Tableau d’avancement :
|
Équation
|
H2CO3
(aq)
|
+ H2O
(ℓ)
|

|
HCO3–
(aq)
|
+
H3O+ (aq)
|
|
état
|
Avancement
x
(mmol)
|
n
(H2CO3)
mmol
|
Solvant
|
|
n
(HCO3–)
mmol
|
n
(H3O+)
mmol
|
|
État
initial
(mmol)
|
0
|
5,0
|
Solvant
|
|
17
|
0
|
|
Au cours
de la
transformation
|
x
|
5,0 – x
|
Solvant
|
17
+ x
|
x
|
|
Avancement
final
|
xf
= xeq
|
5,0 – xeq
|
Solvant
|
17
+ xeq
|
xeq
|
|
Avancement
maximal
|
xmax
|
5,0 – xmax
|
Solvant
|
|
17
+ xmax
|
xmax
|
-
Quantités de matière à
l’équilibre chimique :
-
n
(H2CO3)eq
= 5,0 – xeq ;
n (HCO3–)eq
= 17 + xeq ;
n (H3O+)eq
= xeq
-
Avec la relation suivante :
-
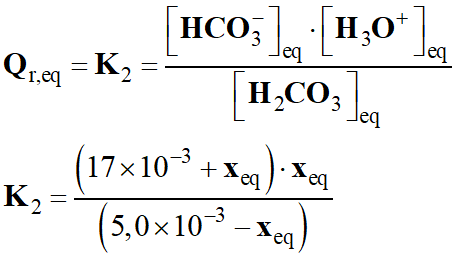
-
En distribuant et en
ordonnant :
-
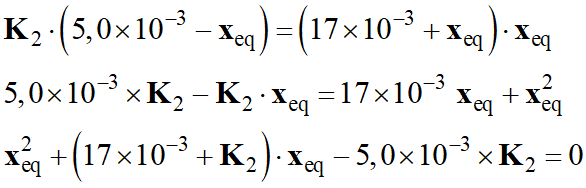
-
On se trouve en présence d’une
équation du second degré en xeq.
-
x2eq
+ (17 + K2 ) .
xeq – 5,0 K2
= 0
-
On peut réaliser
l’approximation suivante :
-
17 × 10–3 +
K2 = 17× 10–3
+ 4,0 × 10–7 ≈ 17× 10–3
-
Équation obtenue :
-
x2eq
+ 17× 10–3 xeq
– 5,0× 10–3 × 4,0 × 10–7 ≈ 0
-
x2eq
+ 17× 10–3 xeq
– 2,0× 10–9 ≈ 0
-
La solution cohérente :
-
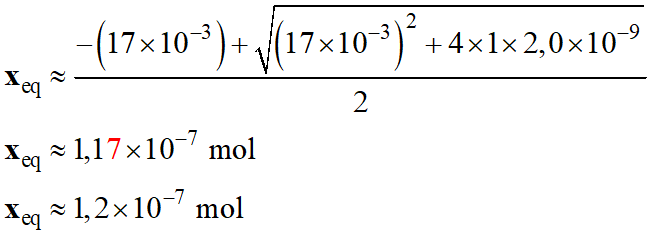
-
Concentration en ions
oxonium :
-
n (H3O+)eq
= xeq
-
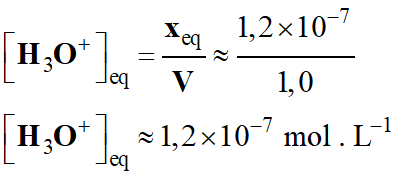
-
Concentration en acide
carbonique à l’équilibre :
-
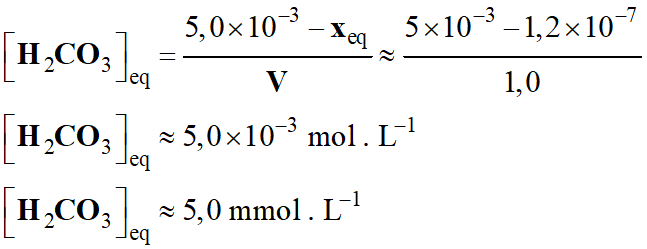
-
Concentration en ion
hydrogénocarbonate à l’équilibre :
-
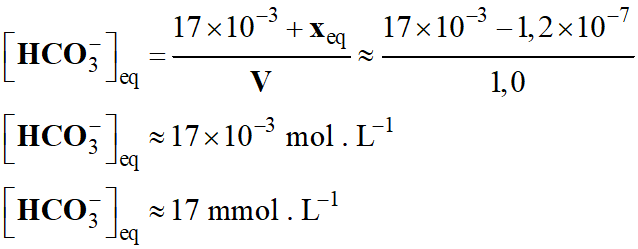
-
La concentration de ces
espèces chimiques n’a pratiquement pas variée au cours de la réaction
(2).
-
Déjà, la réaction
(2)
est une réaction très limitée :
K2 (T) = 4,0 × 10–7 << 1
-
De plus, on note la présence
importante d’ions hydrogénocarbonate HCO3–.
-
Cette présence tend à déplacer
l’équilibre dans le sens inverse de la réaction.
-
pH
de la solution :
-
pH
= - log ([H3O+]eq)
≈ – log (1,2 × 10–7)
-
pH
≈ 6,9
-
Commentaire du résultat.
-
Le
pH a diminué au cours de
l’effort : il est passé de 7,4 à 6,9.
-
Le sportif est sujet à des
crampes (contractions musculaires involontaires, soudaines, bénignes mais
très douloureuses).

III- Exercice 3 :
Pile à combustible au méthanol.
1)-
Énoncé.
Dans de nombreux domaines (bus
électriques, par exemple) il est avantageux de disposer d'une pile pouvant
être continuellement alimentée en réactif.
Une telle pile est appelée « pile à combustible ».
1.
Pile à hydrogène :
Dans une pile à combustible à hydrogène le
dihydrogène est oxydé en ion hydrogène H+ (aq) et le
dioxygène de l'air est réduit en eau.
a)-
Déterminer l'équation de la réaction modélisant la transformation
qui a lieu dans une telle pile.
b)-
Préciser les espèces réagissant au pôle positif, puis celles
réagissant au pôle négatif de cette pile.
c)-
À l'aide éventuellement d'une recherche, indiquer la raison pour
laquelle le stockage du dihydrogène est complexe dans un véhicule.
2.
Première pile au méthanol.
La pile à combustible au méthanol CH3OH
propose une alternative intéressante.
Le principe des premières piles au méthanol
fabriquées est schématisé ci-dessous :
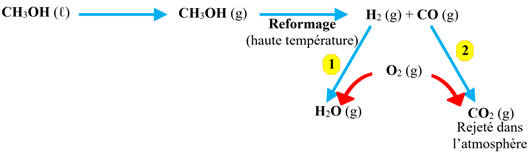
a)-
Déterminer l'inconvénient et
l'avantage présentés par cette pile à combustible au méthanol par rapport à
celle au dihydrogène.
3.
Pile
moderne au méthanol.
Aujourd'hui le méthanol liquide est directement
oxydé dans la pile schématisée ci-dessous.
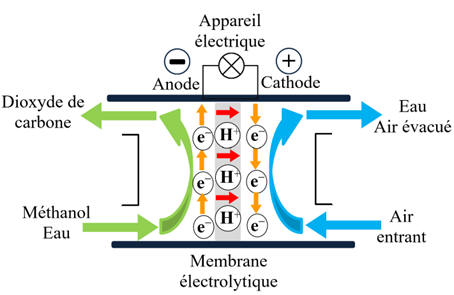
a)-
Montrer
que le bilan de cette pile est identique à celui des anciennes piles à
combustible au méthanol.
b)-
Expliquer quel est l'avantage
des nouvelles piles à combustible au méthanol.
4.
Utilisation dans un
camping-car.
Un camping-car utilise une pile à combustible au
méthanol délivrant un courant électrique d'intensité I = 8,0 A
pendant une durée Δt = 10 h par jour, en moyenne, pour le
fonctionnement des équipements de l'espace de vie.
a)-
Déterminer la charge
électrique utilisée par le camping-car pendant un mois.
b)-
En déduire le volume de
méthanol liquide à acheter chaque mois, la densité de ce dernier étant de
0,79.
c)-
Citer les réducteurs usuels
rencontrés dans cet exercice.

2)- Correction
1.
Pile à hydrogène :
a)-
Équation de la réaction modélisant la
transformation qui a lieu dans une telle pile.
-
Dans une pile à combustible à hydrogène le dihydrogène est
oxydé en ion hydrogène H+
(aq) et le dioxygène de l'air est réduit en eau :
-
Oxydation du dihydrogène :
H2
(g) → 2 H+
(aq) + 2 e–
-
Réduction du dioxygène : ½
O2
(g) + 2 H+
(aq) + 2 e–
→ H2O
(ℓ)
-
Bilan de la
réaction :
|
H2
(g)
|
→
|
2 H+
(aq) + 2 e–
|
|
½ O2
(g) + 2 H+ (aq) + 2 e–
|
→
|
H2O
(ℓ)
|
|
½ O2
(g) + H2 (g)
|
→
|
H2O
(ℓ)
|
b)-
Espèces réagissant au pôle positif et
au pôle négatif de cette pile.
►
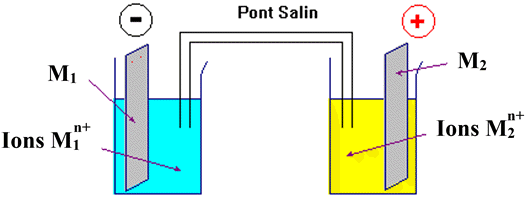
Constitution d’une pile.
(Chap N° 07)
-
Une pile est
constituée de deux compartiments distincts, appelés demi-piles.
-
Chaque compartiment contient un couple oxydant-réducteur du
type Mn+
(aq) / M
(s).
-
Les deux compartiments sont reliés par un
pont salin.
-
La plaque métallique
M
(s) est appelée électrode.
-
Les transferts
d’électrons se produisent à la surface de l’électrode.
-
Une pile
convertit de l’énergie chimique en énergie électrique.
-
Schéma d’une
pile :
-
Schéma général
d’une pile :
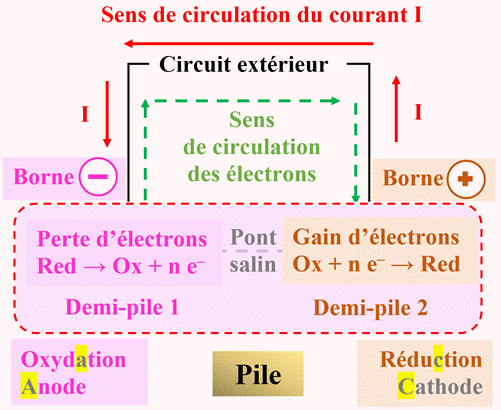
-
Le pôle
– de la pile est le siège d'une
oxydation
(les électrons sont cédés),
-
On l'appelle
l'anode.
-
Le pôle
+
de la pile est le siège d'une
réduction (les
électrons sont captés),
-
On l'appelle la
cathode.
-
L’équation de
la réaction de fonctionnement de la pile est établie en combinant des deux
réactions électrochimiques aux électrodes.
-
En
conséquence :
-
Pôle positif de la pile (Cathode) : Réduction du dioxygène :
O2
(g)
-
Pôle négatif de la pile (anode) : Oxydation du dihydrogène :
H2
(g)
c)-
Stockage du dihydrogène.
-
Le stockage
gazeux :
-
Il consiste à
comprimer le dihydrogène dans des réservoirs à haute pression, généralement
entre 350 et 700 bars.
-
Cette méthode
est utilisée pour les transports, les électrifications et les
stations-service.
-
C’est un
stockage complexe car même fortement compressé il reste à l’état gazeux.
-
C’est aussi un gaz fortement
inflammable.
-
Le stockage liquide :
-
Il consiste à refroidir le
dihydrogène à environ -253 °C pour le liquéfier.
-
Cette méthode est utilisée
pour l’aérospatiale et la recherche.
-
Elle permet d’augmenter la
densité énergétique du dihydrogène, mais elle implique des pertes thermiques
et une consommation d’énergie élevée pour la liquéfaction.
-
Le stockage solide :
-
Il consiste à lier le
dihydrogène à d’autres éléments, comme des métaux ou des hydrures, pour
former des composés solides.
-
Cette méthode est utilisée
pour les prototypes et la recherche.
-
Elle permet de réduire le
volume et la pression du dihydrogène, mais elle nécessite des conditions de
température et de pression spécifiques pour la libération du gaz.
2.
Première
pile au méthanol.
a)-
Détermination des 2 équations
correspondant aux 2 transformations chimiques 1
et 2 mises en jeu.

-
Équation
1 :
|
O2
(g) + 2 H2 (g)
|
→
|
2 H2O
(g)
|
1
|
-
Équation
2 :
|
2 CO
(g) + O2 (g)
|
→
|
2 CO2
(g)
|
2
|
b)-
Bilan, sous forme d'équation de
réaction, d’une telle pile à combustible au méthanol.
|
CH3OH
(ℓ)
|
→
|
2 H2
(g) + CO (g)
|
3
|
-
En combinant les réactions
1,2
et 3 :
|
O2
(g) + 2 H2 (g)
|
→
|
2 H2O
(g)
|
× 2
|
|
2 CO
(g) + O2 (g)
|
→
|
2 CO2
(g)
|
× 1
|
|
CH3OH
(ℓ)
|
→
|
2 H2
(g) + CO (g)
|
× 2
|
|
2 CH3OH
(ℓ) + 3 O2 (g)
|
→
|
4 H2O
(g) + 2 CO2 (g)
|
|
c)-
Inconvénient et l'avantage présentés
par cette pile à combustible au méthanol par rapport à celle au dihydrogène.
-
Avantages :
-
Le méthanol est un liquide à
température ambiante, ce qui facilite son stockage et sa distribution par
rapport à l’hydrogène gazeux.
-
Le méthanol a une densité
énergétique volumique plus élevée que l’hydrogène, ce qui permet de réduire
la taille et le poids des réservoirs.
-
Le méthanol peut être produit
à partir de sources renouvelables, comme la biomasse ou l’électrolyse de
l’eau, ce qui réduit son impact environnemental.
-
Inconvénients :
-
Le méthanol est un produit
toxique et inflammable, ce qui pose des problèmes de sécurité et de
réglementation.
-
Il nécessite une étape de
reformage à haute température difficile à mettre en œuvre.
-
De plus l’étape de reformage
produit du monoxyde de carbone, gaz très toxique pour l’homme.
-
Le méthanol produit du
CO2,
ce qui nécessite un système d’évacuation ou de recyclage du gaz.
3.
Pile
moderne au méthanol.
a)-
Bilan de cette pile à combustible au
méthanol.

-
La pile à combustible au
méthanol est constituée de deux électrodes séparées par une membrane
échangeuse de protons (MEP).
-
À l’anode, le méthanol (CH3OH)
est oxydé en dioxyde de carbone (CO2)
et en protons (H+),
en libérant des électrons (e–).
-
À la cathode, le dioxygène (O2)
est réduit en eau (H2O)
en captant des protons et des électrons (e–).
-
La différence de potentiel
entre les deux électrodes permet de produire un courant électrique.
-
En conséquence les réactifs et
les produits sont identiques.
|
2
CH3OH (ℓ) + 3 O2
(g)
|
→
|
4 H2O
(g) + 2 CO2 (g)
|
b)-
Avantage des nouvelles piles à
combustible au méthanol.
-
L'anode est le compartiment où
le combustible est oxydé, libérant des électrons et des protons.
-
La cathode est le compartiment
où l'oxygène est réduit, absorbant les électrons et les protons pour former
de l'eau.
-
Avantage :
-
Le méthanol est un liquide à
température ambiante, ce qui facilite son stockage et sa distribution par
rapport à l’hydrogène gazeux.
-
le méthanol
CH3OH
(ℓ), n'est pas reformé mais est fourni directement à
la pile à combustible.
-
Inconvénient :
-
Le méthanol diffuse à travers
la membrane de la pile à combustible, ce qui diminue le rendement et la
puissance de la pile.
4.
Utilisation
dans un camping-car.
a)-
Charge électrique
Q
utilisée par le camping-car pendant un mois.
-
Quantité d’électricité
débitée :
|
Q
= I ×
Δt
|
|
Q
|
Quantité d’électricité débitée (C)
|
|
I
|
Intensité du courant (A)
|
|
Δt
|
Durée de fonctionnement (s)
|
-
Un camping-car utilise une pile à combustible au méthanol
délivrant un courant électrique d'intensité I
= 8,0 A pendant une durée Δt
= 10 h par jour, en moyenne, pour le fonctionnement des équipements de
l'espace de vie.
-
Q
= I .
Δt
-
Q
= 8,0 × 10 × (60 × 60) × 30
-
Q
≈ 8,64
× 106 C
-
Q
≈ 8,6 × 106 C
b)-
Volume de méthanol liquide à acheter
chaque mois. (à finir)
-
La quantité d’électricité mise
en jeu au cours du fonctionnement d’une pile est égale à la valeur absolue
de la charge totale des électrons échangés.
-
On écrit :
-
Q
= n (e–)
. NA
. e
-
La valeur absolue de la charge
d’une mole d’électrons définit le faraday de symbole
ℱ.
-
1
ℱ
= | NA
. (–
e)|
-
1
ℱ
≈ 96500 C . mol–1
-
En résumé :
-
Q
quantité d’électricité : grandeur positive : coulomb C
-
n
(e–)
quantité de matière d’électrons échangés : mol.
-
ℱ :
Le faraday : valeur absolue de la charge d’une mole d’électrons.
-
Q
= n (e–)
.
ℱ
Les piles
-
Quantité de matière
n de méthanol utilisé :
-
Il faut utiliser la
demi-équation électronique relative au méthanol :
-
CH3OH
(ℓ) +
H2O (ℓ)
→ CO2 (g) + 6
H+
(aq) + 6 e–
|
Équation
|
CH3OH
(ℓ)
|
+ H2O
(ℓ)
|
→
|
CO2
(g)
|
+ 6 H+
(aq)
|
+ 6 e–
|
|
état
|
Avancement
x
(mol)
|
n (CH3OH)
mol
|
|
|
|
|
n
(e–)
mol
|
|
État
initial
(mol)
|
0
|
n
|
|
|
0
|
0
|
0
|
|
Au bout
de la
durée
Δt
|
x
|
n
– x
= 0
|
|
x
|
6 x
|
6 x
|
|
CH3OH
(ℓ)
|
+ H2O
(ℓ)
|
→
|
CO2
(g)
|
+ 6 H+
(aq)
|
+ 6 e–
|
|
n (CH3OH)
|
|
|
|
|
n
(e–)
|
|
1
|
|
|
|
|
6
|
-
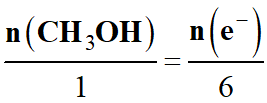
-
On en déduit la relation
suivante :
-
n
(e–)
= 6
n (CH3OH)
-
n
(e–)
= 6 n
-
Quantité de matière de
méthanol à acheter :
-
Q
= n (e–)
.
ℱ
-
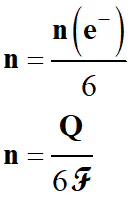
-
Masse de méthanol à acheter :
-
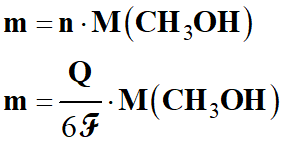
-
Volume de méthanol à acheter :
-
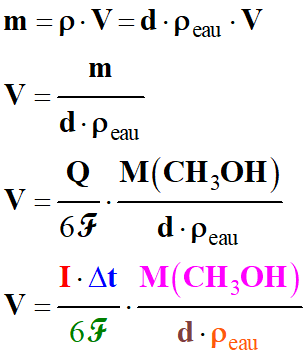
-
Les données :
-
Intensité du courant
électrique : I = 8,0 A ;
-
Durée d’utilisation
journalière :
Δt = 10 h par jour
-
Densité du méthanol :
d = 0,79 ;
-
Masse volumique de l’eau :
ρeau
= 1,0 ×103 g . L–1
-
Masse molaire du méthanol :
M (CH3OH)
= 32 g . mol–1
-
Couples d'oxydoréduction : CO2(g)
/
CH4O(ℓ) et O2(g)
/
H2O(ℓ)
-
Application numérique :
-
Les unités :
-
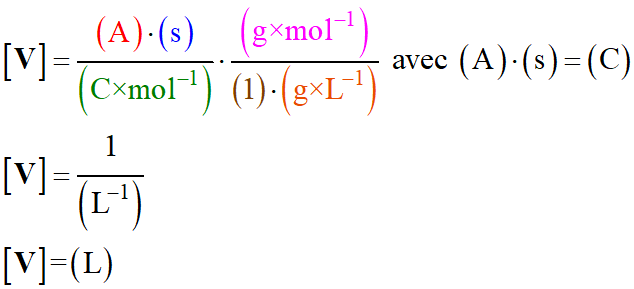
-
Le calcul :
-
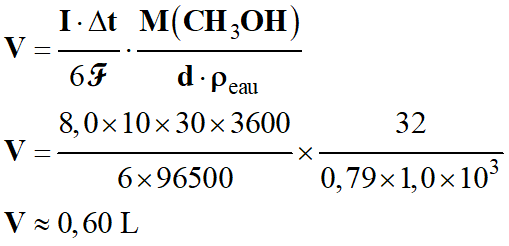
-
Cela fait peu pour un mois
d’utilisation ? Chercher l’erreur ?
-
Certaine pile à combustible au
méthanol (puissance 100 W) annonce 0,90 L de méthanol pour 1 kWh.
-
La tension à vide est
généralement de l’ordre de 0,70 V par cellule.
-
Lorsque la pile fonctionne, la
valeur de la tension entre ses bornes diminue.
-
La tension, lorsque la pile
débite du courant, est souvent comprise entre 0,40 et 0,60 V par cellule.
-
Pour obtenir une tension plus
élevée, il faut associer plusieurs cellules en série.
-
Souvent, les cellules sont
associées en série et en parallèles.
c)-
Citer les réducteurs usuels
rencontrés dans cet exercice.
Les réactions d’oxydoréduction :
-
Un réducteur
est une entité chimique capable de perdre un ou plusieurs électrons.
-
(Réducteur :
perd)
-
Ox
+
n
e
–  Red
Red
-
Exemple :
Cu2+
(aq) + 2
e –
 Cu (s)
Cu (s)
-
Ceci est une
écriture formelle.
-
La double
flèche traduit la possibilité de passer d’une forme à l’autre suivant les
conditions expérimentales.
-
La transformation chimique qui correspond au passage de
l’oxydant Ox
à son réducteur conjugué
Red est une réduction. :
-
Une réduction
est un gain d’électrons.
-
La transformation chimique qui correspond au passage du
réducteur Red
à son oxydant conjugué
Ox est une oxydation :
-
Une oxydation
est une perte d’électrons.
-
Au cours d’une
réaction d’oxydoréduction, un oxydant est réduit et un réducteur est oxydé.
-
En résumé :
|
|
|
|
Réduction
|
|
|
Ox
|
+
|
n
e –
|

|
Red
|
|
|
|
|
Oxydation
|
|
|
Cu2+
(aq)
|
+
|
2
e –
|

|
Cu (s)
|
-
Dans une pile à combustible à
hydrogène le dihydrogène est oxydé en ion hydrogène
H+
(aq)
-
H2
(g) → 2 H+
(aq) + 2 e–
-
Le dihydrogène est un
réducteur.
-
Le méthanol liquide est
directement oxydé dans la pile à combustible au méthanol
-
CH3OH
(ℓ) +
H2O
(ℓ) → CO2
(g) + 6 H+
(aq) + 6 e–
-
Le méthanol est un réducteur.
d)-
La pile à combustible au
méthanol à membrane échangeuse de protons (DMFC).
-
La pile à combustible au
méthanol à membrane échangeuse de protons (DMFC) est un type de pile à
combustible à membrane électrolyte polymère (PEMFC) dans laquelle le
combustible, le méthanol CH3OH (ℓ), n'est pas
reformé mais est fourni directement à la pile à combustible.
-
Le principe de fonctionnement
d'une DMFC est similaire à celui d'une PEMFC classique.
-
L'anode est le compartiment où
le combustible est oxydé, libérant des électrons et des protons.
-
La cathode est le compartiment
où l'oxygène est réduit, absorbant les électrons et les protons pour former
de l'eau.
-
Dans une DMFC,
-
Le méthanol est oxydé à
l'anode en formant du dioxyde de carbone, des protons et des électrons.
-
CH3OH (ℓ) + H2O (ℓ) → CO2 (g)
+ 6 H+ (aq) + 6 e–
-
Les électrons sont collectés
par un circuit externe, générant de l'électricité.
-
Les protons sont transportés à
travers la membrane échangeuse de protons vers la cathode.
-
À la cathode, l'oxygène est
réduit en eau, absorbant les électrons et les protons.
-
½ O2
(g) + 2 H+ (aq) + 2 e– → H2O
(ℓ)
-
La réaction globale de la pile
est la suivante :
-
2 CH3OH (ℓ) + 3 O2
(g) → 2 CO2
(g) + 4 H2O (ℓ)
-
Les DMFC présentent un certain
nombre d'avantages par rapport aux autres types de piles à combustible.
-
Elles sont relativement
compactes et légères, ce qui les rend adaptées aux applications embarquées.
-
Elles ont également une
densité de puissance élevée, ce qui signifie qu'elles peuvent produire une
grande quantité d'électricité par unité de volume.
-
Cependant, les DMFC présentent
également quelques inconvénients.
-
Elles sont plus sensibles à la
contamination que les autres types de piles à combustible.
-
Elles sont également plus
coûteuses.
-
Les DMFC sont en cours de
développement pour des applications telles que les véhicules électriques,
les générateurs portables et les systèmes de stockage d'énergie.
-
Véhicules électriques
:
-
Les DMFC sont une alternative
prometteuse aux batteries pour les véhicules électriques.
-
Elles offrent une autonomie
plus longue et un temps de recharge plus rapide que les batteries.
-
Générateurs portables
:
-
Les DMFC peuvent être utilisés
pour alimenter des générateurs portables, tels que ceux utilisés pour les
camping-cars ou les expéditions en plein air.
-
Systèmes de stockage
d'énergie
:
-
Les DMFC peuvent être
utilisées pour stocker de l'énergie provenant de sources renouvelables,
telles que l'énergie solaire ou éolienne.
-
Les DMFC ont le potentiel de
révolutionner la production d'énergie.
-
Elles pourraient contribuer à
réduire notre dépendance aux combustibles fossiles et à améliorer la qualité
de l'air.

IV- Exercice 4 :
Recette de grand-mère
1)-
Énoncé.
L'argent s’oxyde à l'air en oxyde d'argent, ce qui
ternit bijoux et couverts.
L’utilisation d'aluminium permet de retrouver des
objets brillants.
On s'intéresse dans cet exercice aux différentes
méthodes de nettoyage d'une argenterie oxydée.
DOC. 1 :
Recette de grand-mère pour nettoyer des objets en argent.
1.
Tapisser une bassine en plastique
d'une feuille de papier aluminium.
2.
La remplir avec de l'eau salée très
chaude. Y plonger les objets en argent ternis et attendre quelques minutes.
3.
Ressortir les objets et les rincer à
l'eau claire.
DOC. 2 :
Description d'une pile argent-aluminium.
Une pile est composée de 2 demi-piles reliées par un
pont salin (papier-filtre imbiber une solution de chlorure de potassium).
La première demi-pile est constituée
d'une lame en aluminium de masse m1
= 1,0 g plongeant dans une solution de sulfate d'aluminium
de concentration en quantité d'ions
aluminium Al3+
(aq), C = 0,50 mol . L–1
et de volume V = 50 mL.
La deuxième demi-pile est constituée
d'un fil en argent de masse m2
= 0,50 g plongeant dans une solution de nitrate d'argent
de concentration en quantité d'ions
argent Ag+
(aq), C = 0,50 mol . L–1
et de volume V = 50 mL.
Un conducteur ohmique et un ampèremètre sont
branchés entre la lame en aluminium et le fil d'argent.
L’ampèremètre indique que le courant électrique
circule du fil en l'argent vers la lame en aluminium.
1.
Oxydation et nettoyage des objets
en argent.
a)-
Citer l'oxydant responsable de
l'oxydation des objets en argent au contact de l'air. En déduire l'équation
de la réaction modélisant cette oxydation.
b)-
Indiquer une méthode permettant
d'éviter une telle oxydation.
c)-
Déterminer l'équation de la réaction
modélisant l'action de l'aluminium sur les couverts oxydés.
d)-
Expliquer l'utilisation d’une eau
chaude et non froide.
2.
Pile argent-aluminium.
a)-
Réaliser un schéma légendé de la
pile.
b)-
Compléter le schéma précédent en
indiquant la polarité de la pile. Justifier.
c)-
Écrire les équations des réactions
électrochimiques se produisant sur chaque électrode. En déduire que la
réaction modélisant
la transformation chimique au sein
de la pile quand elle débite du courant électrique est :
3 Ag+
(aq) + Al (s) → 3
Ag (s) +
Al3+
(aq)
La constante d'équilibre de cette
réaction à la température de la pile est : K
(T) = 10125.
d)-
Exprimer puis calculer le quotient de
réaction Qr,i
à l'état initial.
e)-
Déterminer le sens d'évolution du
système étudié et préciser si ce résultat est en accord avec l'indication de
l'ampèremètre.
f)-
Déterminer la capacité électrique de
la pile étudiée.
Données :
-
L’oxyde d’argent
Ag2O
(s) est responsable de la couleur noire des objets en argent oxydés.
-
Masses molaires :
-
M
(Al) = 27,0 g . mol–1
-
M
(Ag) = 107,9 g . mol–1
-
Constante de Faraday : 1
ℱ
= 96,5 × 103 C . mol–1
-
Couples Oxydant / réducteur :
-
Pour l’oxydation par l’air et
le nettoyage des objets en argent :
-
Ag2O
(s) / Ag (s) ;
Al3+
(aq) / Al (s) :
O2
(g) / H2O
(ℓ)
-
Dans la pile :
-
Ag+
(aq) / Ag (s) ;
Al3+
(aq) / Al (s) :
O2
(g) / H2O
(ℓ)

2)- Correction.
1.
Oxydation et nettoyage des
objets en argent.
a)-
Oxydant responsable de
l'oxydation des objets en argent au contact de l'air.
-
C’est le dioxygène de l'air
qui est responsable de l'oxydation des objets en argent.
-
Demi-équations électroniques :
-
2 Ag
(s) + H2O (ℓ) → Ag2O (s) +
2 H+ (aq) + 2 e–
-
½ O2
(g) + 2 H+ (aq) + 2 e–
→ H2O (ℓ)
-
Équation de la réaction
modélisant cette oxydation :
½ O2 (g) + 2 Ag (s) → Ag2O
(s)
b)-
Méthode permettant d'éviter
une telle oxydation.
-
Il faut éviter le contact de
l’objet en argent avec l’air, l’humidité et les produits ménagers.
-
On peut ranger les objets en
argent dans des pochettes hermétiques.
-
Placer l’objet en argent à
côté d’un morceau de craie qui observera l’humidité et ralentira
l’oxydation.
-
Nettoyer régulièrement les
objets en argent avec des produits comme :
- l’hydrogénocarbonate de sodium,
(bicarbonate), le vinaigre blanc (acide éthanoïque), le sel (chlorure de
sodium) ou le citron,
-
On peut utiliser le procédé
décrit dans le DOC.1(Recette de grand-mère pour nettoyer des objets en
argent).
c)-
Équation de la réaction
modélisant l'action de l'aluminium sur les couverts oxydés.
-
Les demi-équations
électroniques :
-
Ag2O
(s) + 2 H+ (aq) + 2 e–
→ 2 Ag (s) + H2O (ℓ)
-
Al
(s) → Al3+ (aq) + 3 e–
-
Équation de la réaction :
3 Ag2O (s) + 2 Al (s)
+ 6 H+ (aq) → 6 Ag (s) + 2 Al3+
(aq) + 3 H2O (ℓ)
d)-
Utilisation d’une eau chaude
et non froide.
-
La température est un facteur
cinétique. Avec l’eau chaude, la réaction est plus rapide.
-
Pourquoi de l’eau salée ?
-
L’eau salée crée un milieu
conducteur entre les deux métaux.
-
L’eau salée favorise la
réaction entre l’oxyde d’argent et l’aluminium.
2.
Pile argent-aluminium.
a)-
Schéma légendé de la pile.
Voir dessous
b)-
Schéma légendé de la pile avec
circuit extérieur.
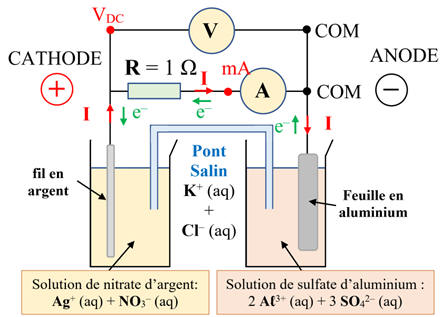
-
Justification :
-
D’après l’ampèremètre le
courant circule dans le circuit extérieur du fil d’argent vers la feuille
d’aluminium.
-
Les électrons circule dans le
sens inverse de la borne négative vers la borne positive.
-
Le fil d’argent constitue la
borne positive (cathode) et la feuille d’aluminium la borne négative (anode)
de la pile ainsi constituée.
c)-
Équations des réactions
électrochimiques se produisant sur chaque électrode.
-
Anode : Al (s) → Al3+
(aq) + 3 e–
-
L’aluminium Al (s) est
oxydé en ion aluminium Al3+ (aq).
-
Cette réaction libère les
électrons qui se déplace dans le circuit électrique de l’électrode
d’aluminium vers l’électrode d’argent.
-
Cathode : Ag+
(aq) + e– → Ag (s)
-
Au contact de l’électrode
d’argent les ions argent Ag+ (aq), présents dans la
solution, sont réduits en argent métal Ag (s).
-
Cette réaction consomme les
électrons provenant de l’électrode d’aluminium par le circuit électrique.
-
Bilan de la réaction :
3 Ag+ (aq) + Al (s) → 3
Ag (s) + Al3+ (aq)
-
La constante d'équilibre de
cette réaction à la température de la pile est : K (T) = 10125.
d)-
Expression et calcul du
quotient de réaction Qr,i à l'état initial.
Système ne comportant que des
espèces dissoutes.
-
Considérons la réaction chimique
non totale suivante :
-
Considérons la réaction chimique non
totale suivante :
a
. A
(aq) +
b
.
B
(aq)
 c
. C
(aq) +
d
.
D
(aq)
c
. C
(aq) +
d
.
D
(aq)
-
Par définition, le quotient de réaction
Qr
de cette réaction s’écrit :
|
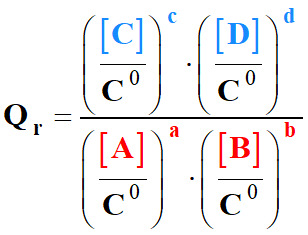
|
|
Qr
|
Quotient de réaction (sans unité)
|
|
[C]
et [D]
|
Concentration des produits (mol . L–1)
|
|
[A]
et
[B]
|
Concentration des réactifs (mol . L–1)
|
|
C0
|
Concentration standard : C0 =
1,0 mol . L–1
|
►
Remarque :
-
Pour simplifier l’expression, on omet
de mettre la concentration standard C0.
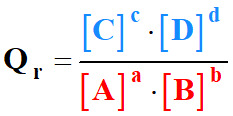
- Mais, il ne faut pas oublier que le
quotient de réaction
est une grandeur sans unité
qui caractérise un système chimique dans un état donné :
-
Par convention, l’eau,
solvant, n’intervient pas dans
l’écriture de l’expression de Qr
(même s’il intervient dans l’équation de la réaction).
-
Les espèces chimiques solides n’apparaissent pas
dans l’expression du quotient de réaction.
-
Quotient de réaction dans le cas présent :
3 Ag+ (aq) + Al (s) → 3
Ag (s) + Al3+ (aq)
-
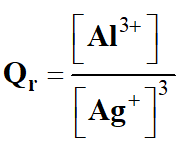
-
Quotient de réaction initial :
-
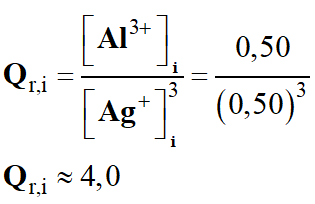
e)-
Sens d'évolution du système
étudié.
-
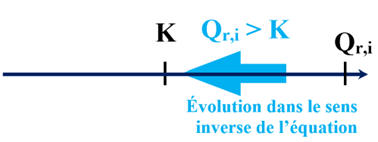
En conséquence Qr,i
< K, la réaction s’effectue dans le sens direct de
l’écriture de la réaction.
-
La
transformation évolue dans le sens direct de l’équation :

|
|
Sens direct
K
|
|
|
3 Ag+
(aq) + Al (s)
|
→
|
3 Ag
(s) + Al3+ (aq)
|
|
|
Sens inverse
1 / K
|
|
-
Ce résultat est en
accord avec l'indication de l'ampèremètre
-
Comme K >> 104,
la réaction est quasi-totale.
f)-
Capacité électrique de la pile
étudiée.
►
Capacité électrique d’une
pile :
-
La capacité électrique d’une
pile est la charge électrique maximale
Qmax que la pile peut
débiter durant sa durée de vie.
|
Qmax
= n (e–)max . NA
. e
|
|
Qmax
|
Capacité
électrique de la pile (coulomb : C)
|
|
n
(e–)max
|
Quantité
maximale d’électrons échangés (mol)
|
|
NA
|
Nombre
d’Avogadro (mol–1)
NA =
6,02 × 1023 mol–1
|
|
e
|
Charge
élémentaire (coulomb : C)
e = 1,60 × 10–19
C
|
►
Remarque :
-
La quantité maximale
n (e–)max
d’électrons échangés se détermine à partir de la quantité du
réactif limitant.
-
Il ne faut pas confondre la
capacité électrique d’une pile Qmax
avec le quotient de réaction Qr
d’une réaction chimique.
-
Quantité de matière les
espèces présentes :
-
Quantité de matière initiale
d’aluminium Al (s)
-
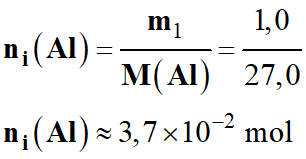
-
ni
(Al) ≈ 37 mmol
-
Quantité de matière initiale
d’ions aluminium Al3+(aq)
-
ni
(Al3+) = C .
V
-
ni
(Al3+) = 0,50 × 50 ×
10–3
-
ni
(Al3+) ≈ 2,5 × 10–2
mol
-
Quantité de matière initiale
d’argent Ag (s)
-
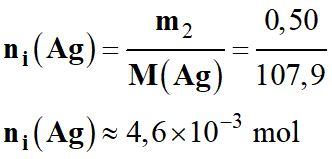
-
Quantité de matière
initiale d’ions argent Ag+ (aq) :
-
ni
(Ag+) = C .
V
-
ni
(Ag+) = 0,50 × 50 ×
10–3
-
ni
(Ag+) ≈ 2,5 × 10–2
mol
-
ni
(Ag+) ≈ 25 mmol
-
K
> 104, la réaction est totale.
-
En conséquence :
|
|
|
|
Sens direct
|
|
|
|
|
3 Ag+
(aq)
|
+
|
Al
(s)
|
→
|
3 Ag
(s)
|
+
|
Al3+
(aq)
|
-
Tableau d’avancement :
-
Les réactifs sont Ag+
(aq) et Al (s)
|
Équation
|
3 Ag+
(aq) +
|
Al
(s)
|
→
|
3 Ag
(s)
|
+
Al
3+
(aq)
|
|
État
|
Avancement
x
(mmol)
|
|
|
|
|
|
|
État
initial (mmol)
|
0
|
ni
(Ag+)
= 25
|
ni
(Al)
= 37
|
ni
(Ag)
= 4,6
|
ni
(Al3+)
= 25
|
|
État
Intermédiaire
|
x
|
ni
(Ag+) – 3
x
|
ni
(Al) – x
|
ni
(Ag) + 3 x
|
ni
(Al3+)
+ x
|
|
État
final
|
xf
= xmax
|
ni
(Ag2+) –
3 xmax
= 0
|
ni
(Al) – xmax
|
ni
(Ag) + 3 xmax
|
ni
(Al3+)
+ xmax
|
|
xmax
= 8,3
|
0
|
29
|
30
|
33
|
-
Le réactif limitant : l’ion
Ag+ (aq) est le réactif limitant
-
Capacité électrique de la
pile :
-
Qmax
= n (e–)max
. NA .
e
-
Maintenant, pour pouvoir
déterminer la valeur de la capacité électrique de la pile, il faut connaître
le nombre maximal d’électrons échangés.
-
Il faut utiliser la
demi-équation électronique relative aux ions argent,
Ag+, (réactif
limitant) faisant intervenir les électrons :
-
En conséquence :
n (e–)max
= ni (Ag+)
≈ 25 mmol
-
Qmax
= n (e–)max
. NA .
e
-
Qmax
= xmax .
NA .
e
-
Qmax
≈ 25 × 10–3 × 6,02 × 1023 × 1,60 × 10–19
(mol . mol–1 . C)
-
Qmax
≈ 2,4 × 103 C

V- Exercice 5 :
Protection de la coque contre la corrosion.
1)-
Énoncé.
Les bateaux
dont la coque est un acier sont victimes de la corrosion et doivent être
protégés.
Une méthode consiste à déposer à la surface de leur
coque des blocs de métal appelés « électrodes sacrificielles».
L'objectif de l'exercice est d'évaluer la masse de
l'électrode sacrificielle nécessaire à la protection d'un bateau.
DOC.1 :
Potentiels standard
Tous les couples oxydant-réducteur sont
caractérisés par une grandeur appelée potentiel standard.
Pour prévoir les réactions d'oxydoréduction
possibles entre différents oxydants et réducteurs à disposition, il est
possible de s'appuyer en première approche sur l'échelle suivante appelée
échelle des potentiels standard.
Échelle des potentiels standard (en volt V) de
quelques couples à 25 ° C :
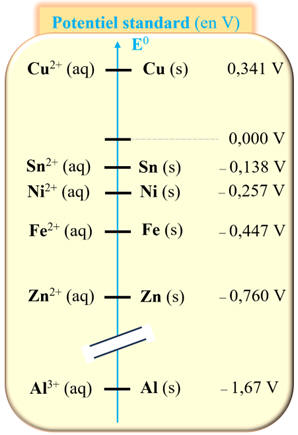
Lorsque deux métaux sont en contact et peuvent être
oxydés par le dioxygène, celui dont le couple a le potentiel standard le
plus faible s'oxyde :
Il constitue l'anode et protège votre métal, qui ne
réagira pas avec le dioxygène.
DOC. 2 :
Protection d’une coque en acier.
L'oxydation de l'électrode sacrificielle est
modélisée par une réaction d'équation électrochimique de type :
M → Mk+ + k e–
(électrode)
Où M est le métal de l’anode et k un
entier positif.
Lors de cette oxydation une circulation d'électrons
se met en place et il s'établit un courant électrique de protection au
niveau de la surface d'aire S de la coque immergée.
Sa densité de courant électrique moyenne, intensité
de courant par unité de surface vaut :
j = 0,10 A . m–2
DONNÉES :
-
La coque du bateau et sa carène sont
entièrement en acier (essentiellement constitué de fer).
-
Sa longueur est de 18 m,
la largeur immergée moyenne de la
carène et de 4,5 m et l'angle moyen de cette carène avec l'horizontale vaut
20°.
-
Masse molaire :
-
M (Zn) = 65,4 g . mol–1
-
M (H2O) =
18,0 g . mol–1
-
Constante de Faraday :
-
1
ℱ =
n (e–)max
. NA = 9,65 × 104
C . mol–1
-
1
ℱ = 96500 C . mol–1

Questions :
1.
Questions préliminaires :
a)-
Citer, en justifiant, les matériaux du
DOC.1 susceptibles de
protéger la coque en acier d’un bateau.
b)-
Évaluer l’aire de la surface de coque immergée.
2.
Problème :
L’objectif est de protéger la coque en acier du
bateau par une électrode sacrificielle en zinc, à remplacer quand elle a
perdu 50 % de sa masse.
Déterminer la masse minimale de zinc à répartir sur
la coque pour la protéger pendant un an.

2)- Correction.
1.
Questions préliminaires :
a)-
Matériaux du DOC.1
susceptibles de protéger la coque en acier d’un bateau.
-
Exploitation de l’ énoncé et des potentiels standard :
-
Lorsque deux métaux sont en contact et peuvent être oxydés par le dioxygène,
celui dont le couple a le potentiel standard le plus faible s'oxyde.
-
On peut considérer que la coque est en fer.
-
Le zinc et l’aluminium ont des potentiels standard plus faibles que le fer.
-
On peut utiliser le zinc et l’aluminium pour protéger les coques en acier de
bateaux.
-
Ils constituent l'anode et protège l’acier, qui ne réagira pas avec le
dioxygène.
-
Ceci tant que le métal est présent.
b)-
Aire de la surface de coque immergée.
-
On peut considérer que la surface immergée est constituée de deux triangles
rectangles identiques avec les dimensions suivantes :
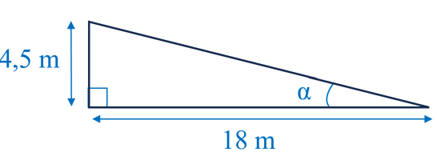
-
Estimation de l’aire S de la surface de la coque immergée :
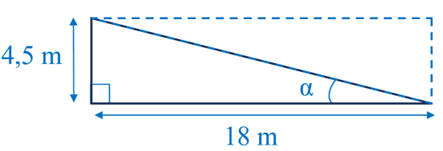
-
S ≈ 18 × 4,5
-
S ≈ 81 m2
1.
Problème :
-
Masse minimale de zinc à répartir sur la coque pour la protéger pendant un
an.
-
Les données :
-
Masse molaire :
-
M (Zn) = 65,4 g . mol–1
-
M (H2O) = 18,0 g . mol–1
-
Constante de Faraday :
-
1
ℱ =
n (e–)max .
NA = 9,65 × 104
C . mol–1
-
1
ℱ = 96500 C . mol–1
-
Sa densité de courant électrique moyenne, intensité de courant par unité de
surface vaut :
-
j = 0,10 A . m–2
-
Masse de zinc nécessaire pour protéger la coque du bateau pendant la durée
Δt = 1 an :
-
Grandeur : m (g)
-
L’objectif est de protéger la coque en acier du bateau par une électrode
sacrificielle en zinc, à remplacer quand elle a perdu 50 % de sa masse.
-
La masse de zinc ayant réagi :
-
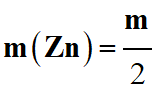
-
Avec m (Zn ) = n
(Zn) . M (Zn )
-
m = 2 m (Zn)
-
Quantité de matière de zinc nécessaire :
-
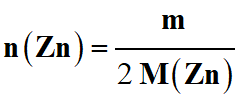 (1)
(1)
-
La réaction chimique :
-
Le système ainsi constitué se comporte comme pile constituée d’une électrode
de zinc et d’une électrode de fer.
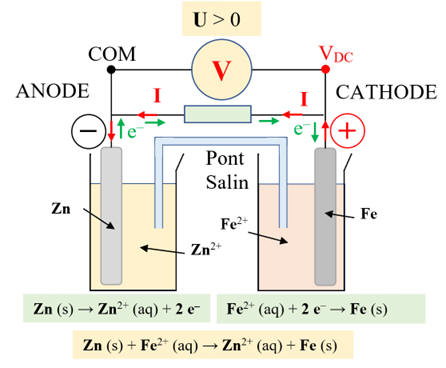
-
Cette réaction consomme du zinc Zn (s) suivant la demi-équation
électronique :
-
Zn (s) → Zn2+ (aq) + 2 e–
-
Relation entre la quantité de matière de zinc et la quantité de matière
d’électrons :
|
Zn
(s
|
→
|
Zn2+
(aq)
|
+ 2 e–
|
|
n
(Zn)
|
|
n
(Zn2+)
|
n
(e–)
|
|
1
|
|
|
2
|
- 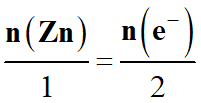
-
n (e–) = 2
n (Zn)
-
Pour connaître la quantité de matière d’électrons échangés, il faut utiliser
la quantité d’électricité mise en jeu :
-
La capacité électrique d’une pile est la charge électrique maximale
Qmax que la pile peut
débiter durant sa durée de vie.
|
Qmax
= n (e–)max . NA
. e
|
|
Qmax
|
Capacité
électrique de la pile (coulomb : C)
|
|
n
(e–)max
|
Quantité
maximale d’électrons échangés (mol)
|
|
NA
|
Nombre
d’Avogadro (mol–1)
NA =
6,02 × 1023 mol–1
|
|
e
|
Charge
élémentaire (coulomb : C)
e = 1,60 × 10–19
C
|
Remarque :
-
La quantité maximale n (e–)max
d’électrons échangés se détermine à partir de la quantité du
réactif limitant.
-
Dans le cas présent, le réactif limitant est le zinc Zn (s).
-
Q = n (e–) . NA . e
-
Q = 2 n (Zn) . NA . e
-
Q = 2 n (Zn) .
ℱ
(2)
-
Autre relation permettant d’exprimer la quantité d’électricité :
-
Quantité d’électricité débitée :
|
Q
= I ×
Δt
|
|
Q
|
Quantité d’électricité débitée (C)
|
|
I
|
Intensité du courant (A)
|
|
Δt
|
Durée de fonctionnement (s)
|
-
On connait la densité de courant électrique moyenne, intensité de courant
par unité de surface :
-
j = 0,10 A . m–2
-
Avec I = j . S
-
I = 0,10 × 81
-
I ≈ 8,1 A
-
La durée d’utilisation est de 1 an :
-
Δt = 365 × 24 × 3600
-
Δt = 3,15 × 107 s (on peut garder trois chiffres
signification à ce niveau)
-
Il n’est pas nécessaire de faire les différents calculs.
-
Q = j . S . Δt
(3)
-
En combinant les relations (2) et (3 )
-
2 n (Zn) .
ℱ = j . S . Δt
-
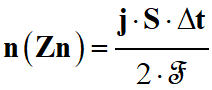 (4)
(4)
-
Pour avoir la masse de zinc m : on combine la relation obtenue (4)
avec la relation (1)
-
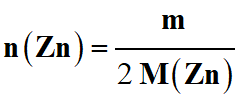 (1)
(1)
-
En conséquence :
-
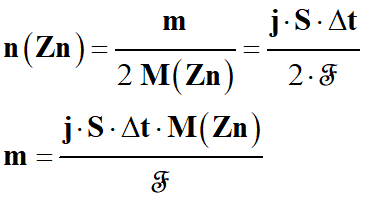
-
Application numérique :
-
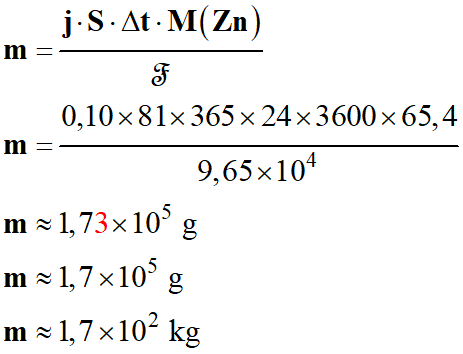
-
Cela semble beaucoup pour une surface immergée de 80 m2.
-
Cette masse est à répartir sur la surface immergée de la coque.

-
L’acier est un métal qui peut se corroder au contact de l’eau salée, de
l’oxygène ou de certains produits chimiques.
-
Il existe plusieurs méthodes de protection de la coque en acier :
-
La peinture anti-corrosion :
-
Elle consiste à appliquer une couche de peinture spéciale qui empêche
l’oxydation de l’acier et le protège des agressions extérieures.
-
La peinture doit être renouvelée régulièrement pour assurer son efficacité.
-
Le traitement antirouille :
-
il consiste à traiter les zones de la coque qui présentent des signes de
corrosion avec un produit qui neutralise la rouille et la transforme en une
couche protectrice.
-
Le traitement doit être effectué dès l’apparition des premières taches de
rouille pour éviter qu’elles ne s’étendent.
-
Les anodes sacrificielles :
-
il s’agit de blocs de métal, généralement en zinc ou en magnésium, qui sont
fixés à la surface de la coque et qui s’oxydent à la place de l’acier.
-
Les anodes créent un courant électrique qui protège la coque de la corrosion
galvanique.
-
Les anodes doivent être remplacées lorsqu’elles sont trop usées.
-
On fixe les anodes sacrificielles à l’aide de vis ou de boulons.
-
Elles sont placées à proximité des parties métalliques les plus exposées à
l’oxydation, comme l’hélice, le gouvernail, les échappements ou les prises
d’eau.
-
Il faut aussi veiller à ce que les anodes soient en contact électrique avec
la coque, en évitant les isolants comme la peinture ou le vernis.
-
Les anodes doivent être réparties de manière homogène sur la coque, en
respectant une distance minimale entre elles pour éviter les interférences.
-
La masse totale des anodes doit être proportionnelle à la surface de la
coque à protéger.