I- La poussée d’Archimède.

1)- Fluide incompressible :

-  Un fluide incompressible est un fluide dont la masse volumique ρ est constante.

-  Il s’agit d’un modèle.

-  Conditions :

-  Le fluide doit avoir une température T constante et homogène ;

-  Sa vitesse d’écoulement v est petite devant la célérité c des ondes acoustiques qui peuvent se déplacer dans le fluide :

-   

2)- Origine de la poussée d’Archimède.

a)-  Force pressante :

-  La force pressante résulte des chocs entre les entités, qui constituent le fluide, et les parois du récipient.

-  Un fluide exerce une force pressante sur les parois du récipient qui le contient :

-  Schéma :

-  Remarque :

-  La valeur de la force pressante ne dépend pas de l’orientation de la paroi (les particules se déplacent dans toutes les directions de façon désordonnée).

-  Lorsqu’un fluide au repos est au contact d’une paroi, il exerce sur celle-ci une force pressante .

-  Schéma :

-  La valeur F de la force pressante dépend de la pression P du fluide et de la surface de contact S

-  Relation :

b)-  Pression dans l’eau et profondeur :

-  La pression de l’eau augmente avec la profondeur.

-  La pression de l’eau s’ajoute à celle de l’air.

-  On ajoute 1 × 10⁵ Pa tous les 10 m.

-  Par définition, l’unité légale de pression est le pascal de symbole Pa.

-  C’est la pression exercée par une force pressante de 1 N sur une surface plane de 1 m².

-  On emploie couramment d’autres unités :

-  Le bar  (bar) : 1 bar = 10⁵ Pa

-  L’hectopascal : 1 hPa = 10² Pa = 1 mbar

-  Exemple : cas de l’eau

c)-  Loi fondamentale de la statique des fluides :

-  Relation :

-  Schéma :

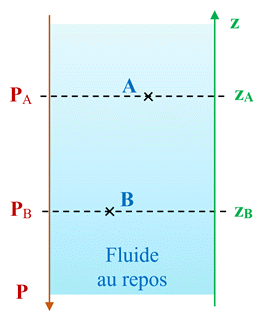
-  Deux points A et B, situés dans un même liquide au repos, de mêmes coordonnés verticales (z_A = z_B) sont à la même pression (P_A = P_B).

-  Deux points A et B, situés dans un même liquide au repos, de coordonnés verticales différentes (z_A ≠ z_B) sont à des pressions différentes (P_A ≠ P_B).

-  Si z_A > z_B, alors P_B > P_A

d)-  Forces pressantes exercées par un fluide sur un solide immergé.

-  Schéma :

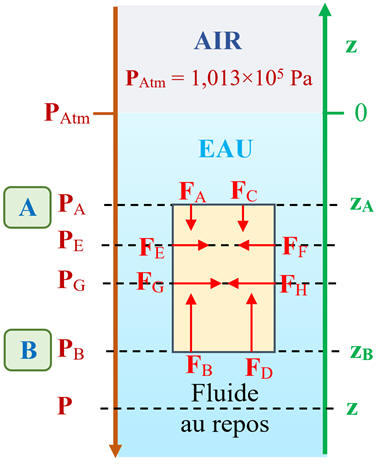
-  Considérons les deux positions verticales A et B :

-  z_A > z_B, alors P_B > P_A ; on en déduit que pour une même surface S, F_B > F_A 

-  Les forces pressantes ne se compensent pas.

-  Considérons les deux positions verticales E et F :

-  z_E = z_F, alors P_E = P_F ; on en déduit que pour une même surface S, F_E = F_F

-  On remarque que les forces horizontales se compensent deux à deux.

-  Alors que les forces verticales ne se compensent pas.

►  Conclusion :

-  La somme des forces pressantes exercées sur le solide immergé est de direction verticale et orientée vers le haut.

-  Ce résultat est général et ne dépend pas de la forme du solide immergé.

e)-  Origine de la poussée d’Archimède :

-  Dans un fluide au repos, la différence de pression entre les parties inférieure et supérieure d’un solide immergé est à l’origine de la poussée d’Archimède.

-  La résultante des forces pressantes exercées sur un corps immergé dans un fluide incompressible au repos est appelée poussée d’Archimède.

-  Expérience : mise en évidence :

-  Expérimentation

3)- Expression vectorielle de la poussée d’Archimède.

-  La poussée d’Archimède  exercée par un fluide de masse volumique ρ_fluide est égale à l’opposé du poids du fluide déplacé.

-  Pour un corps ayant un volume immergé V_im, l’expression vectorielle est donnée par la relation suivante :

-  Schéma :

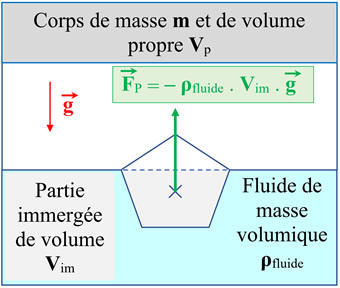
-  Valeur de la poussée d’Archimède :

-  Remarque :

-  L’existence de la poussée d’Archimède est liée à la présence du champ de pesanteur .

II- La conservation du débit volumique.

1)- Régime permanent indépendant du temps.

-  Pour décrire l’écoulement d’un fluide incompressible, on subdivise le fluide en unités appelées particules de fluide.

-  Une particule de fluide est un système fermé de dimensions mésoscopiques.

-  Dimensions mésoscopiques : elles sont de l’ordre du 0,1 µm.

-  Elles sont petites par rapport à l’échelle macroscopique mais suffisamment grandes pour contenir un grand nombre d’entités microscopiques.

►  Les vecteurs vitesses des particules de fluides :

-  Ils sont tangents en tout point à des courbes appelées lignes de champ de vitesse ou ligne de courant.

-  Les lignes de champ de vitesse permettent de cartographier le champ de vitesse du fluide.

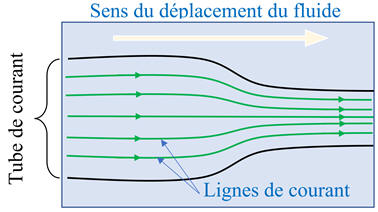
►  Régime permanent :

-  Un fluide s’écoule en régime permanent indépendant du temps, si la valeur v de la vitesse en chaque position est indépendante du temps t.

-  En régime permanent, la valeur v de la vitesse d’écoulement en tout point ne varie pas au cours du temps t.

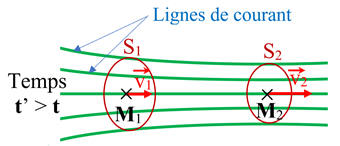
-  En régime permanent, en tout point

-  Ainsi, en régime permanent,  au point M₁ du fluide, la valeur de la vitesse v₁ ne change pas au cours du temps.

-  De même au point M₂ du fluide la valeur de la vitesse v₂ ne change pas au cours du temps.

2)- Débit volumique.

-  En régime permanent, le débit volumique D_V d’un fluide correspond au volume V de fluide qui traverse une section droite S pendant une durée Δt.

-  Relation :

-  Le débit volumique D_V est une caractéristique de l’écoulement d’un fluide.

-  Conséquence :

-  Pendant la durée Δt :

-  Le fluide traverse une section de surface S ;

-  Le fluide parcourt la distance ℓ avec la vitesse d’écoulement v :

-   ℓ = v . Δt

-  On en déduit l’expression du volume V de fluide écoulé à travers la section S :

-  V = S . ℓ

-  V = S . v . Δt

-  Schéma :

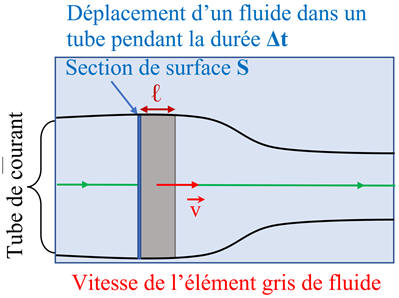
-  On en déduit la relation suivante :

-   

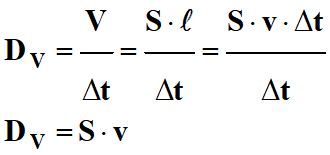
►  Débit volumique D_V :

-  Le débit volumique D_V est égal au produit de la surface S de la section de tube traversée par le fluide, par la valeur v de la vitesse du fluide au niveau de cette section.

3)- Conservation du débit volumique d’un fluide incompressible.

-  Un fluide incompressible s’écoule en régime permanent dans une canalisation constituée de deux tubes de sections différentes.

-  Schéma de la situation :

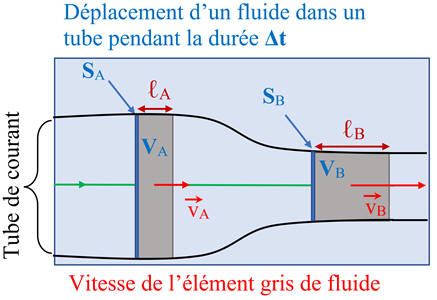
-  Le volume V_A de fluide se déplaçant dans la canalisation de section S_A est identique au volume V_B de fluide se déplaçant dans la canalisation de section S_B ceci pendant la même durée Δt.

-  V_A = V_B

-  En conséquence, pendant la durée Δt :

-   

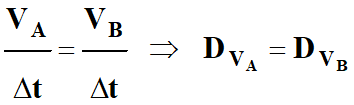
-  D_V = D_VA = D_VB

-  Le débit volumique est donc constant :

-  D’autre part ,

-  D_V = S_A . v_A = S_B . v_B

-  Comme S_A > S_B, alors v_A < v_B

►  Conclusions :

-  Au cours d’un écoulement en régime permanent, le débit volumique d’un fluide incompressible se conserve. Il ne varie pas.

-  Pour un fluide incompressible, le débit volumique D_V est le même en tout point du fluide.

-  Si la surface S ↓ de fluide traversée diminue, la valeur de la vitesse v ↑ d’écoulement du fluide augmente.

III- Relation de Bernoulli.

1)- Introduction.

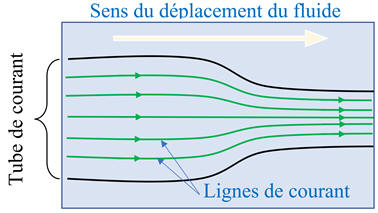
-  Lorsqu’un fluide s’écoule, la trajectoire d’une particule de fluide est appelée lignes de champ de vitesse ou ligne de courant.

-  Une ligne de courant est orientée dans le sens de déplacement du fluide.

-  L’ensemble des lignes de courant d’un fluide constitue un tube de courant dans lequel le fluide s’écoule.

2)- Énoncé de la relation de Bernoulli.

-  On considère :

-  Un fluide incompressible qui s’écoule en régime permanent indépendant du temps.

-  Que les frottements sont négligeables

-  Que les forces pressantes  sont les seules forces non conservatives qui s’exercent sur un élément de fluide se déplaçant le long d’une ligne de courant d’une position A à une position B :

-  Schéma de la situation :

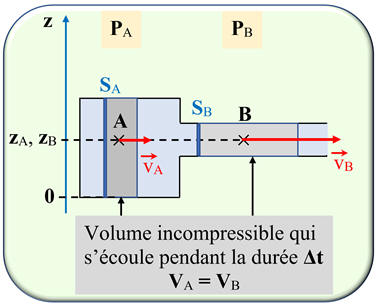
-  On admet que le travail de ces forces pressantes est donné par la relation :

-   

-  Relation :

-  On considère que l’élément du fluide a une masse m :

-  On peut en déduire la variation de l’énergie mécanique de cet élément de fluide :

-   

-  Avec :

-   

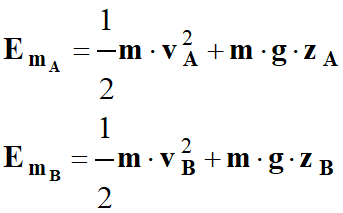
-  En remplaçant dans l’expression suivante :

-   

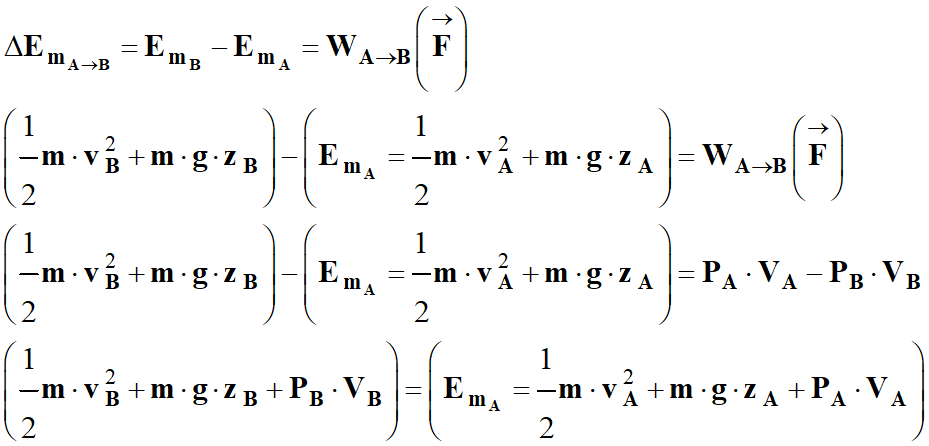
-  Que l’on peut écrire aussi sous la forme suivante :

-   

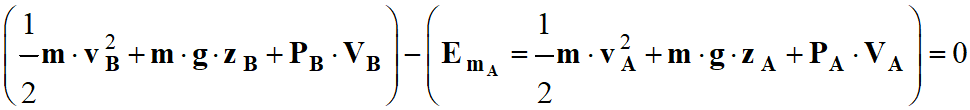
►  Conclusion :

-  On remarque que le long d’une ligne de courant le fluide incompressible en régime permanent vérifie la relation suivante :

-   

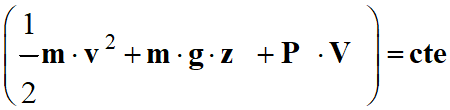
-  Sachant que pour un fluide incompressible , m = ρ . V

-  En divisant, la relation précédente par le volume V de l’élément de fluide, on obtient la relation suivante :

-   

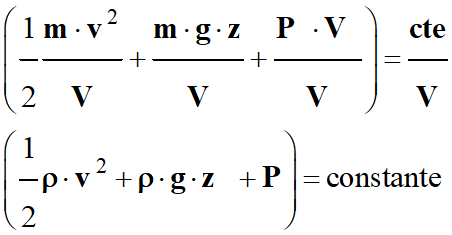
-  On obtient ainsi la relation de Bernoulli.

-  Relation de Bernoulli :

-  Remarque :

-  La relation de Bernoulli est constituée de deux termes :

-  Le terme : ρ . g . z + P

-  Ce terme traduit la pression statique.

-  Il est lié à la relation fondamentale de la statique des fluides.

-  Le terme :

-  Ce terme traduit la pression dynamique.

-  Il est lié à la force pressante qui s’applique sur un corps maintenu immobile dans un écoulement de fluide à la vitesse v.

-  Ce terme permet de tenir compte des corrections à apporter à la loi fondamentale de la statique des fluides lorsque le fluide étudié n’est plus au repos.

►  La relation de Bernoulli :

-  Elle relie en toute position du fluide d’une même ligne de courant :

-  La pression P ;

-  La valeur de la vitesse v ;

-  La coordonnée verticale z de la position.

-  Pour une même ligne de courant :

- 

3)- Effet Venturi.

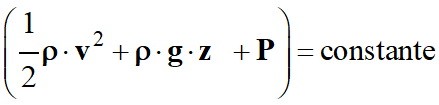
►  Écoulement d’un fluide dans un tube dont la section diminue :

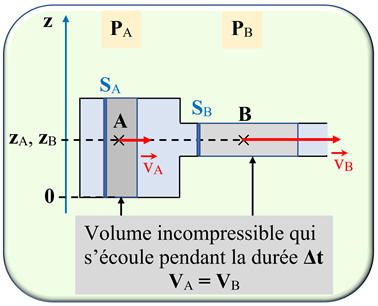
-  Schéma de la situation :

-  On applique la relation de Bernoulli à l’écoulement d’un fluide incompressible dans un tube qui se resserre.

-  La section de la surface S se resserre :  S_A > S_B

-  Comme le fluide est incompressible et que l’écoulement s’effectue en régime permanent indépendant du temps, le débit volumique est conservé :

-  D_V = D_VA = D_VB

-  Les deux points A et B sont à la même altitude :

-  z_A = z_B

-  On applique la relation de Bernoulli à cette situation :

-   

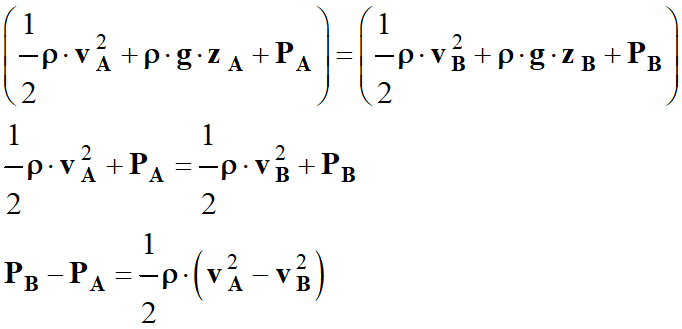
-  À la lecture de cette relation, on peut en déduire que :

-  v_B > v_A => P_B < P_A

-  Une valeur de la vitesse en B supérieure à la valeur de la vitesse en A, entraîne une pression plus petite en B qu’en A :

-  C’est l’effet Venturi.

IV- Applications.

1)- Mise en évidence de la poussée d’Archimède.

2)- QCM.

3)- Exercices.