|
TP Physique N° 03 |
Tension d'un ressort. Réalisation d'un dynamomètre. Équilibre d'un solide. La Poussée d'Archimède. Correction. |
|
|
||
 |
|
TP Physique N° 03 |
Tension d'un ressort. Réalisation d'un dynamomètre. Équilibre d'un solide. La Poussée d'Archimède. Correction. |
|
|
||
|
|
|
=> Déterminer la condition nécessaire d’équilibre d’un solide soumis à des forces. |
|
|
=> Définir la tension d’un ressort. |
|
|
=> En déduire la notion de tension d’un ressort. |
|
|
=> Expliquer comment réaliser un dynamomètre. |
|
|
=> Mettre en évidence la poussée d’Archimède. |
- L’extrémité A du ressort étant fixe, on suspend des masses marquées de valeurs croissantes à son autre extrémité B.
- Pour chaque valeur de la masse m, on mesure l’allongement x du ressort lorsque le système S = {masse marquée} est immobile (on dit aussi en équilibre) dans le référentiel d’étude.
- Soit
le vecteur poids du système
S.
- La valeur du poids est notée P.
- Construire un tableau sur le modèle suivant et faire une douzaine de mesures.
- Ne pas dépasser
|
Masse m en g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Poids P en N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x en cm |
|
|
|
|
|
|
|
|
|
|
|
|
|
Faire un schéma du dispositif.
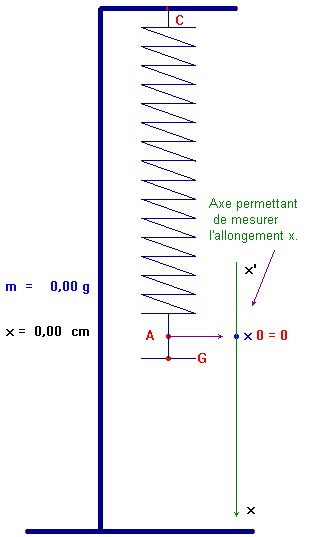
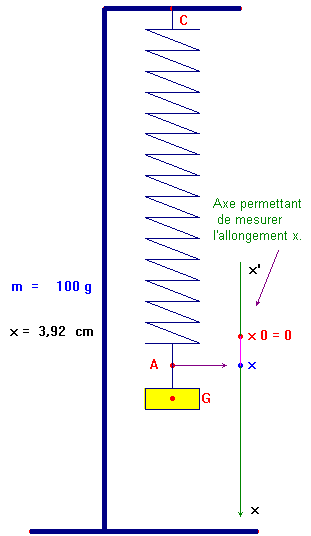
- Indiquer le référentiel d’étude.
|
- Le référentiel d’étude est
le support. C’est un référentiel terrestre. |
- Faire le bilan des forces s’exerçant sur le système S lorsque celui-ci est en équilibre.
|
- Le système
S (c’est-à-dire la masse
marquée) - Il
est
soumis à l’action exercée
par - L’action exercée par - Il est soumis à l’action du ressort (action de contact). -
L’action exercée par le ressort sur le système
S est appelée, tension du ressort :
|
- D’après le Principe de l’inertie vu en classe de seconde (et que vous énoncerez) donner la condition d’équilibre d’un solide soumis à des forces (condition nécessaire mais non suffisante).
|
- Principe de l’Inertie : - Énoncé : tout corps persévère dans son état de repos
ou de mouvement rectiligne uniforme si les
forces qui s’exercent sur lui se compensent. - Condition d’équilibre :
|
- Donner les caractéristiques de l’action exercée par le ressort sur le système S (point d’application, direction, sens et valeur).
-
L’action exercée par le ressort sur le système
S
est appelée, tension du ressort :
notation vectorielle et
T
représente la valeur de cette tension en newton.
|
-
Caractéristiques du vecteur
Poids :
|
|
- On va déduire les caractéristiques
du vecteur tension du ressort
- Caractéristiques du vecteur
tension d’un ressort :
|
|
- Représentation graphique du
système
S
à l’équilibre :
|
- Représenter graphiquement les variations de la valeur de la tension T que le ressort exerce sur
la masse marquée en fonction de son allongement x, c’est-à-dire T = f (x).
-
Tableau de valeurs :
|
masse
m |
Poids
P
= T |
allongement
x |
|
en
g |
en
N |
en
cm |
|
0 |
0,00 |
0,00 |
|
10 |
0,10 |
0,39 |
|
30 |
0,29 |
1,18 |
|
50 |
0,49 |
1,96 |
|
70 |
0,69 |
2,75 |
|
90 |
0,88 |
3,53 |
|
110 |
1,08 |
4,32 |
|
130 |
1,28 |
5,10 |
|
150 |
1,47 |
5,89 |
|
170 |
1,67 |
6,67 |
|
190 |
1,86 |
7,46 |
|
210 |
2,06 |
8,24 |
|
230 |
2,26 |
9,03 |
|
250 |
2,45 |
9,81 |
|
Pour
réaliser un graphe, il faut toujours faire figurer : - le titre du graphe - les grandeurs portées en abscisse (axe horizontal) et
en ordonnée (axe vertical) - les unités utilisées - l’échelle utilisée. Le
choix de l’échelle tient toujours compte de la plus grande valeur
mesurée (voir exemple plus loin). Le
graphe doit avoir une taille raisonnable et les longueurs des axes ne
doivent pas être trop différentes. |
- Donner les caractéristiques de la fonction obtenue.
- Tracer la droite moyenne et déterminer la valeur du coefficient directeur de celle-ci.
- Ce coefficient est une grandeur caractéristique du ressort.
- On l’appelle la constante de raideur du ressort, notée k.
- Donner sa valeur et son unité dans le S.I.
|
- Les points notés sont sensiblement alignés :
-
on peut représenter l’ensemble de ces
points par une droite.
- On dit alors que l’on trace
la droite moyenne.
- c’est-à-dire :
- cette
droite passe par le maximum de points expérimentaux
- les
écarts entre les points et cette droite sont les plus petits
possibles - il
doit rester autant de points au-dessus qu’en dessous de la droite
moyenne tracée. |
|
- Il existe une relation simple
entre la valeur de la tension
T exercée par le ressort et
son allongement
x. - La droite moyenne passe par
l’origine. - L'équation de cette droite est du type y = a x , ici T = a x.
- Où "a"
est le coefficient
directeur de la droite.
- "a" est appelé aussi, en
physique, la pente
de la droite. - Dans les cas présent, on note
a =
k constante de raideur du ressort. - On calcule le coefficient directeur de cette droite en prenant
-
un point
M
de la droite moyenne, le
plus éloigné possible de l'origine des axes.
- Ce point
M ne correspond à
aucun
point du tableau de mesures.
- D'une manière générale on écrit
:
-
Ici on notera :
|
- Remarque : une méthode qui marche toujours que la droite passe par l’origine ou non.
-
|
- On peut écrire que :
|
- Remarque : on peut faire une exploitation du tableau de valeurs avec le tableur Excel.
- Tableau de valeurs :
- On trace la courbe T = f (x).
- On peut faire une étude statistique avec Excel et tracer la courbe de tendance (On choisit le modèle linéaire)
- On demande d'afficher l'équation de la courbe et le coefficient de détermination R.
Cliquer sur l'image pour l'agrandir
-
- Le coefficient de détermination R ≈ 1, il y a dépendance linéaire entre les deux grandeurs.
- La valeur de la tension T du ressort est proportionnelle à la valeur x de l'allongement du ressort.
- Le coefficient de proportionnalité :
- k = a ≈ 0,2499 N / cm
- k = a ≈ 25 N / m
III- Réalisation d’un dynamomètre.
Un dynamomètre permet de mesurer l’intensité d’une force.
-
- À l’aide de l’étude précédente, proposer un protocole permettant la réalisation d’un dynamomètre.
-
- Le but
de l’étude qui suit est de donner les caractéristiques de 
a)- Étape 1 :
- Suspendre une masse marquée de masse
m
=
- Noter la valeur de l’allongement x du ressort et en déduire la valeur de la tension T exercée par le ressort sur la masse marquée.
|
- Remarque : - le ressort étudié a une raideur
k
= 23 N / m.
|
|
|
Allongement |
x1
en cm |
4,25 |
|
Tension du ressort |
T1
en N |
0,98 |
b)- Étape 2 :
- Immerger la masse marquée suspendue au ressort, dans une éprouvette graduée contenant de l’eau.
- Noter la valeur de l’allongement x’ du ressort et en déduire la valeur de la tension T’exercée par le ressort sur la masse marquée.
|
|
|
Allongement |
x2
en cm |
3,65 |
|
Tension
du ressort |
T2
en N |
3,65
x
10 – 2 x 23 =
0,84 |
3)- Exploitation.
- Faire le bilan des forces exercées sur le système S = {masse marquée} lors de l’étape 1.
|
- Bilan des forces :
- L’action exercée par
- L’action exercée par le ressort sur le système S :
|
|
- Faire le bilan des forces exercées sur le système S = {masse marquée} lors de l’étape 2.
|
- Bilan des forces :
- L’action exercée par -
- L’action exercée par le
ressort sur le système
S : -
- On remarque que
x2 <
x1,
la valeur de la tension diminue lorsque l’on immerge le solide - L’action exercée par le
fluide (ici l’eau) sur le système
S. - Comme le poids est inchangé et que la valeur de la tension exercée par le ressort diminue, - le fluide exerce une force sur l’objet. - C’est la poussée d’Archimède qui n’est pas négligeable par rapport au poids dans l’eau. - |
|
- En déduire les caractéristiques de
.
|
- Le système est en équilibre. - D’après la réciproque du Principe de l’Inertie, le système S est soumis à des forces
dont les effets se compensent. -
- Comme les vecteurs forces,
- D’autre part,
x’
<
x
, le sens de la force est du
bas vers le haut (de
G
vers
A). - La valeur de |
|
|
► Point d’application : Centre de poussée
C |
|
► Direction : la droite (AG) (verticale) |
|
|
► Sens : du bas vers le haut : de
G vers
A. |
|
|
► Valeur :
π
= π =
P
– T2
≈ 0,14 N |
4)- Calcul du poids du volume d’eau déplacé : Pe.
- Déterminer le volume d’eau déplacé par lecture sur l’éprouvette graduée.
|
|
|
|
- Valeur du volume d’eau déplacée : - V =
V2
-
V1
- V
≈ 225 - 211 - V
≈ 14 mL = 14 cm3 |
- En déduire la valeur de la masse me de l’eau déplacée, puis la valeur de Pe.
|
- Valeur de la masse d’eau déplacée : -
me =
μ .
V - me
≈
1,00 x 12 - me
≈ - Poids du volume d’eau déplacée : - Pe =
me .
g - Pe
≈
14 x
10 – 3 x 9,81 - Pe
≈ 0,14 N |
5)- Comparaison entre Pe et π.
- Comparer les valeurs de Pe et de p et conclure.
|
- Valeur de - π
=
P
–
T2
- π
≈ 0,98 – 0,84 - π
≈ 0,14 N - Pe
≈
π |
- Récapitulatif : donner les caractéristiques de la poussée d’Archimède.
|
Poussée d’Archimède :
|
=> Point d’application : Centre de poussée C :
le centre du
fluide déplacé |
|
=> Direction : Verticale du lieu passant par C. |
|
|
=>
Sens : Du bas vers le haut. |
|
|
=> Valeur : π
= µ0 .
g .
V
ou π
= ρ0 .
g
. V unité :
newton (N) |
