|
Partie I : Première phase de vidange : h
> H
Schéma de la situation :
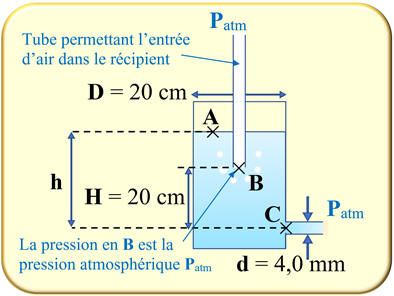
1.
Valeur
vA
de la vitesse en A.
-
Exploitation
du graphique :
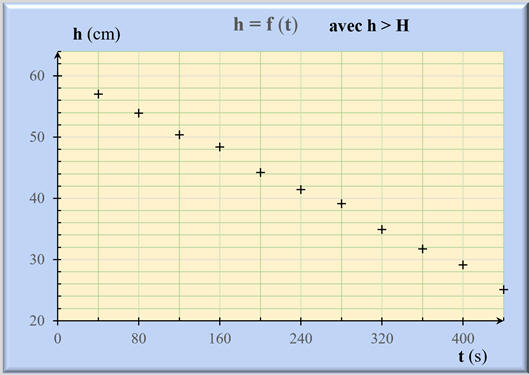
-
On relève la hauteur
h d’eau dans le vase
cylindrique à chaque instant
t jusqu’à la vidange :
-
La courbe obtenue :
h =
f
(t)
-
Les points
sont sensiblement alignés.
-
La courbe obtenue est du type :
h
= a .
t
+ b
-
La grandeur
h
est une fonction affine décroissante du temps
t.
-
On peut obtenir l’équation de cette droite en réalisant
une étude statistique avec le tableur
Excel
ou en
traçant la droite moyenne.
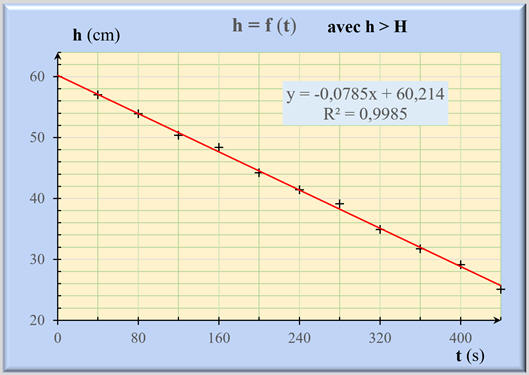
-
Traduction :
-
h
≈ – 0,079 t
+ 60
-
Le coefficient
de détermination :
-
R2
= 0,9985 ≈ 1
-
Le modèle
choisi est en accord avec les mesures de l’expérience réalisée.
-
Que représente
le coefficient directeur de la droite moyenne tracée ?
-
a
= – 0,079 cm . s–1
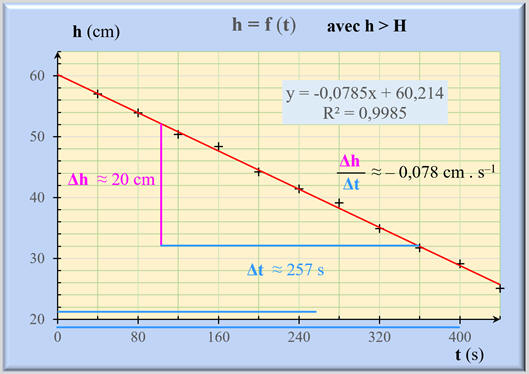
-
Détermination
graphique :
-
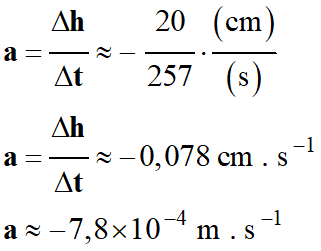
-
Le coefficient directeur de la droite tracée représente,
en valeur absolue, la valeur
vA de la vitesse d’écoulement de l’eau au point
A.
-
Cette valeur
est constante au cours du temps .
-
On pose :
a = –
vA
-
On obtient :
-
h
≈ – vA
. t + 60
-
vA
≈ 0,078 cm . s–1
-
vA
≈ 7,8 × 10–4 m .
s–1
-
L’ordonnée à
l’origine :
-
b
≈ 60 cm, c’est la hauteur
h0
de l’eau à l’instant initial, au temps
t
= 0 s.
2.
Vitesse de
déplacement du fluide :
a.
Valeur
vA
de la vitesse en A
et le débit volumique DV.
►
Débit
volumique DV
:
-
Le débit volumique
DV
est égal au produit de la surface
S
de la section de tube traversée par le fluide, par la valeur
v
de la vitesse du fluide au niveau de cette section.
|
DV
= S . v
|
DV :
Débit volumique (m3 . s–1)
|
|
S :
surface de la section de tube traversée par le fluide (m2)
|
|
v
: valeur de la vitesse du fluide au niveau de cette section
(m . s–1)
|
-
Dans le cas
présent :
-
La valeur
vA
de la vitesse au point
A est constante
-
De même la valeur du diamètre
D
de la section du tuyau est constante.
-
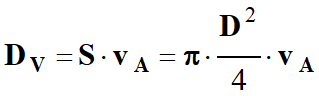
-
Or :
-
On considère
l’eau comme un liquide incompressible et elle s’écoule en régime
permanent indépendant du temps :
-
En conséquence
le débit volumique se conserve DV.
-
DV
= DVA =
DVC
-
Valeur du
débit volumique :
-
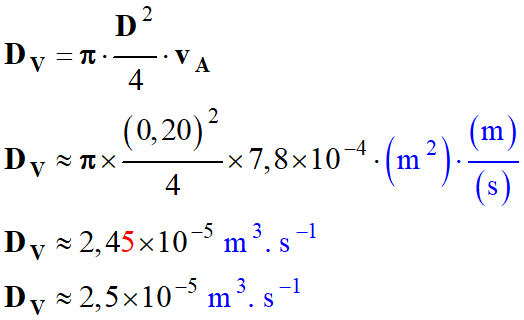
b.
Valeur
vC
de de la vitesse de sortie de l’eau en
C.
-
DV
= DVA =
DVC
-
Avec :
-
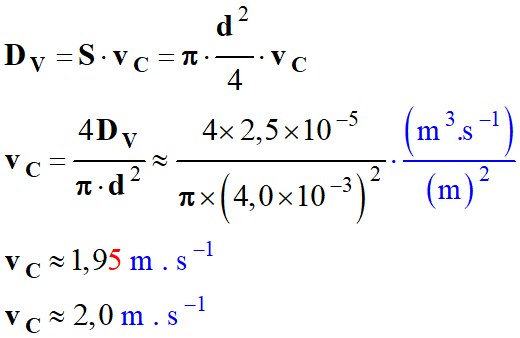
-
Comme le tube d’écoulement est plus petit, la vitesse
d’écoulement du fluide au point
C
est plus grande que celle au point
A.
c.
Protocole
expérimental :
-
Montage :
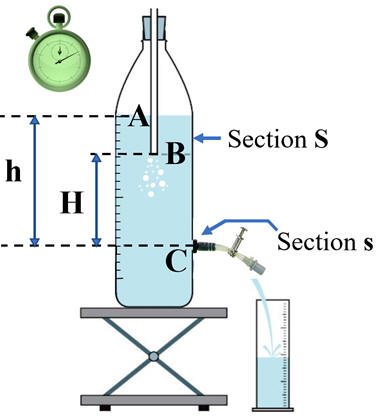
-
On choisit une
durée d’écoulement de l’eau :
-
Dans le cas présent, la valeur choisie
Δt
= 40 s.
-
Remarque :
-
On peut choisir la durée
Δt et mesurer le volume
V
ou on peut choisir le volume
V et mesurer la durée
Δt.
-
À l’aide de l’éprouvette graduée, on mesure le volume
V
correspondant à cette durée.
-
Ainsi, on en déduit la valeur
DV
du débit volumique :
-
En régime permanent, le débit volumique
DV
d’un fluide correspond au volume
V de fluide qui traverse une section droite
S
pendant une durée
Δt.
-
Relation :
|
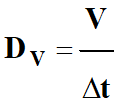
|
DV :
Débit volumique (m3 . s–1)
|
|
V :
Volume de fluide (m3)
|
|
Δt
: durée (s)
|
-
Le débit volumique
DV
est une caractéristique de l’écoulement d’un fluide.
3.
Loi de Torricelli :
a.
Valeur
vC
Torr de la vitesse prévue par la loi de
Torricelli en C.
-
Expression de
la loi de Torricelli :
-
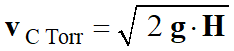
-
Application
numérique :
-
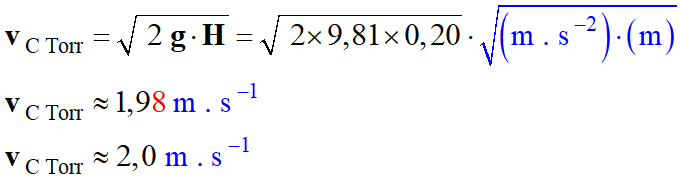
b.
La valeur trouvée à
la question 2. b.
et celle obtenue par cette loi :
-
La valeur trouvée à la question
2. b.
est en accord avec celle obtenue par la loi de Torricelli.
Partie II Deuxième phase de vidange :
h < H
-
Évolution du
débit volumique en C lorsque
h < H
-
Exploitation
du graphique :
-
On relève la hauteur
h d’eau dans le vase
cylindrique à chaque instant
t jusqu’à la vidange :
-
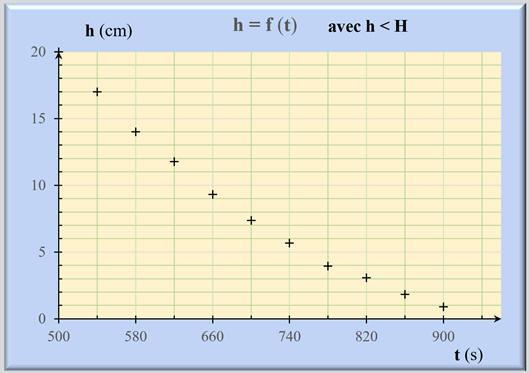
La courbe obtenue :
h =
f
(t)
-
Les points ne
sont pas alignés.
-
La courbe obtenue n’est pas du type :
h
= a .
t
+ b
-
La hauteur
h est une fonction décroissante
du temps
-
La hauteur de
fluide décroit de moins en moins vite au cours du temps.
-
Pour des intervalles de temps égaux, la variation de
hauteur de liquide écoulé
Δh est de plus en plus faible.
-
En conséquence, la vitesse d’écoulement du fluide au
point C
diminue au
cours du temps.
-
Il découle de
ceci que le débit volumique de l’eau diminue au cours du temps.
-
Le débit volumique n’est plus constant lorsque
h
< H.
-
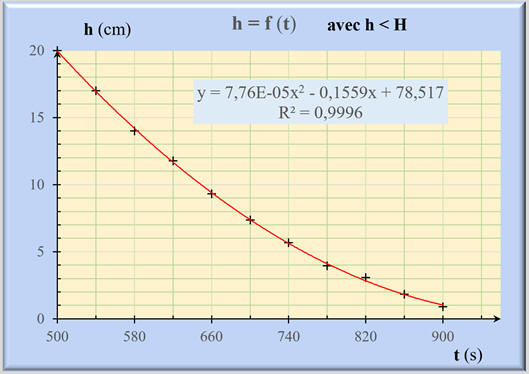
On peut faire une étude statistique avec le tableur
Excel :
-
Le modèle
choisi : « Polynomiale » : Degré 2
-
Traduction du
résultat :
-
h
≈ a
. t2
+ b
. x
+ c
-
h
≈ 7,76 × 10-5
t2
– 0,156 t
+ 78,5 pour 0 <
h
< 20 cm
-
Le coefficient
de détermination :
-
Le coefficient
de détermination :
-
R2
= 0,9996 ≈ 1
-
Le modèle
choisi est en accord avec les mesures de l’expérience réalisée avec
l’intervalle d’étude.
-
Pour affiner
l’étude , il faut :
-
Plus de mesures et un intervalle de temps
Δt
plus court entre deux mesures.
-
Dans le cas présent, l’intervalle de temps
Δt
= 40 s
-
La durée de
l’expérience est de 400 s
-
Il faut faire en sorte que
Δt << 400 s.
-
On peut choisir
Δt = 5,0 s ou même
Δt
= 2,0 s.
-
Si la mesure de la hauteur
h est trop difficile, on peut
mesurer la masse m d’eau qui s’écoule pendant la
durée Δt.
-
Graphique
complet :
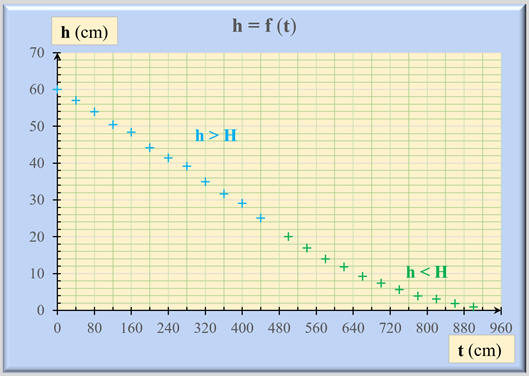
- Tableau de valeurs :
|
t
en s
|
h
en cm
|
|
0
|
60,0
|
|
40
|
57,0
|
|
80
|
53,9
|
|
120
|
50,4
|
|
160
|
48,4
|
|
200
|
44,2
|
|
240
|
41,4
|
|
280
|
39,1
|
|
320
|
34,9
|
|
360
|
31,7
|
|
400
|
29,1
|
|
440
|
25,10
|
|
500
|
20,0
|
|
540
|
17,0
|
|
580
|
14,0
|
|
620
|
11,8
|
|
660
|
9,30
|
|
700
|
7,37
|
|
740
|
5,68
|
|
780
|
3,96
|
|
820
|
3,08
|
|
860
|
1,84
|
|
900
|
0,90
|
|