I- L’action mécanique et son modèle : Le vecteur force.

1)- Exemple  : Ressort que l’on tend à l’aide d’une ficelle.

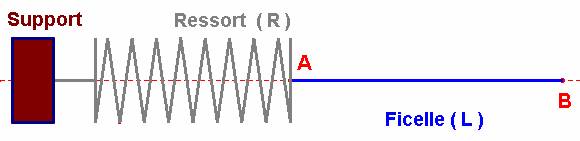
-  Quelles sont les caractéristiques de l’action exercée par la ficelle sur le ressort ?

-  L’action mécanique localisée au point A, exercée par la ficelle L sur le ressort R, est appelée : force exercée par L sur R.

2)- Caractéristiques d’une force.

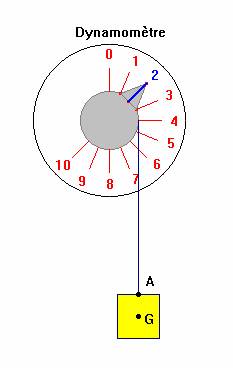
3)- Mesure de l’intensité d’une force.

-  L’intensité d’une force se mesure à l’aide d’un dynamomètre.

-  L’unité légale de force est le newton de symbole N.

-  Remarque :

-  Un dynamomètre mesure aussi bien la force qu’on lui applique que la force qu’il exerce.

4)- Le vecteur force.

-  La force exercée par la ficelle (L) sur le ressort (R) peut être modélisée par un vecteur noté .

-  Ce vecteur indique la direction et le sens de l’action exercée par L sur R.

-  La norme du vecteur est égale à l’intensité de la force, la valeur de la force que l’on note :

-  

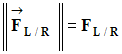
-  Elle s’exprime en newton N

-  Pour représenter le vecteur force, une échelle est nécessaire.

-  Exemple : 1 cm  ↔ 1 N

-  Représenter la force  sachant que  F _{L / R} = 5 N  

5)- Conclusion.

-  Un objet subit des actions mécaniques de la part de certains objets qui l’entourent

-  On appelle force l’action mécanique d’un objet sur un autre.

-  Lorsque deux systèmes A et B sont en interaction, A exerce une force sur B et B exerce une force sur A.

II- Les différents types de forces.

1)- Forces de contact et forces à distance.

-  Une action mécanique de contact s’exerce uniquement entre 2 objets en contact l’un de l’autre.

-  Sans contact, pas de force de contact.

-  Exemple :

-  Livre posé sur une table horizontale.

-  Le livre exerce une action sur la table et la table exerce une action sur le livre.

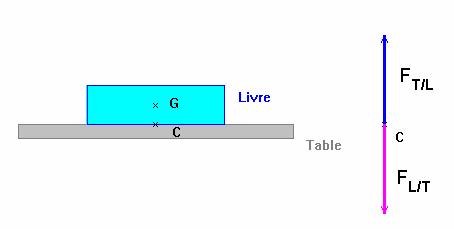
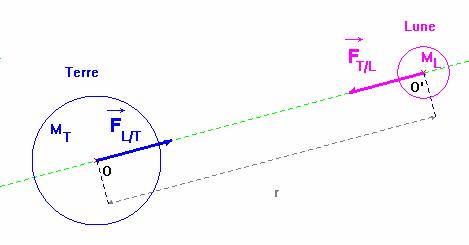
-  Une action à distance peut s’exercer entre deux objets en interaction. 

-  C’est le cas de l’interaction gravitationnelle, de l’interaction électrostatique. 

-  Dans ce cas, pas besoin de contact pour avoir interaction.

2)- Forces localisées et forces réparties.

-  Exemple :

-  On peut considérer que l’action exercée par la ficelle sur le ressort est localisée au point A. 

-  Dans ce cas, on peut parler d'action localisée.

-  Dans le cas du livre posé sur la table, l’action mécanique entre la table et le livre est répartie sur toute la surface de contact. 

-  La résultante de toutes ces actions élémentaires est appelée force de contact répartie en surface.

-  Le poids d’un objet :

-  Le poids d’un objet est réparti sur tout le volume de l’objet.

-  Le poids est une force à distance répartie en volume.

-  Pour représenter ces forces, on utilise le même modèle que pour la force localisée.

-  Caractéristique du poids  d’un objet :

3)- Somme et décomposition de vecteurs forces.

a)- Somme de deux forces.

-  Considérons un solide S soumis à deux forces  et . 

-  L’action de ces deux forces peut être représentée par un vecteur force unique égal à la somme vectorielle des deux vecteurs forces considérés.

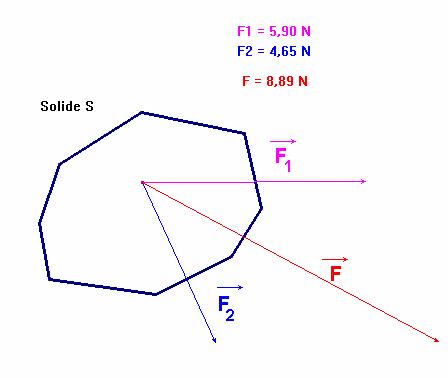
-  Quand les points d’applications sont différents, on choisit le point d’application de la résultante.

b)- Décomposition d’une force.

-  Il est souvent très utile de décomposer un vecteur force  en deux vecteurs forces perpendiculaires.

-  Ces deux forces sont appelées composantes et leur somme vectorielle est égale au vecteur force .

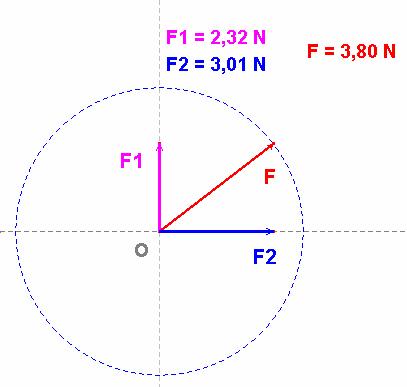
- Relations :   et 

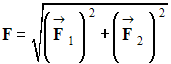
III- Méthodologie : Caractérisation des forces s’exerçant sur un solide.

-  Cette opération est appelée : bilan des forces.

-  On définit le système étudié et on l’isole du milieu extérieur.

-  On identifie les actions mécaniques qui agissent sur le système.

-  Il faut répondre à la question : avec qui le système est-il en interaction ?

-  On modélise les actions mécaniques par des forces.

-  On représente ces forces en choisissant une échelle convenable.

Voir un exemple :

IV- Quelques exemples.

1)- Réaction d’un support :

-  Livre posé sur une table.

-  On considère un livre de masse m = 250 g posé sur une table plane et horizontale. 

-  Quelles sont les actions mécaniques que subit le livre ?

-  Réponse : 

-  Le système étudié est le livre.

-  On l’isole : on le représente seul.

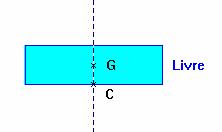
-  Le livre est en interaction avec la Terre. Il est soumis à son poids . 

-  Le livre est en interaction avec la table, il est soumis à la force  que l’on appelle la réaction du support.

-  Caractéristiques de chacune des forces :

-  Pour déterminer les caractéristiques de la réaction du support, on utilise le principe de l’inertie. 

-  Le livre est en équilibre, il est au repos. 

-  D’après la réciproque du principe de l’inertie, le livre est soumis à des actions mécaniques dont les effets se compensent.

-  On en déduit que :

-  Schéma :

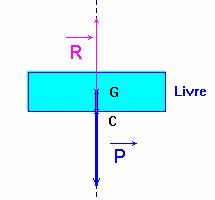
2)- Réaction du support bis : livre sur un plan incliné.

-  On considère un livre de masse m = 250 g posé sur un plan incliné d’un angle α = 20 ° par rapport à l’horizontale. 

-  Quelles sont les actions mécaniques que subit le livre ?

-  Réponse : 

-  Le système étudié est le livre. On l’isole.

-  Le livre est en interaction avec la Terre. Il est soumis à son poids . 

-  Le livre est en interaction avec le support, il est soumis à la force  que l’on appelle la réaction du support.

-  Caractéristiques de chacune des forces :

-  Pour déterminer les caractéristiques de la réaction du support, on utilise le principe de l’inertie. 

-  Le livre est en équilibre, il est au repos. 

-  D’après la réciproque du principe de l’inertie, le livre est soumis à des actions mécaniques dont les effets se compensent.

-  On en déduit que :

-  Schéma :

-  Remarque : On peut décomposer la réaction du support  en deux actions :

-  La réaction normale au support qui empêche le livre de traverser la table.

-  Généralement, on la note .

-  La réaction tangentielle  qui empêche le livre de glisser sur le support. 

-  Elle est liée aux forces de frottement.

-  Généralement, on la note .

-  Relation :

-  Schéma :

-  Valeurs :

-  Remarque : si les frottements sont négligeables, la réaction  est normale au plan du support.

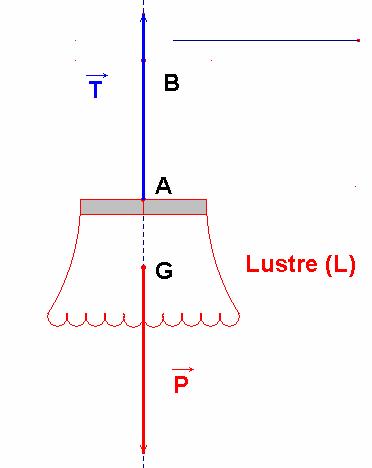
3)- Actions mécaniques s’exerçant sur un lustre.

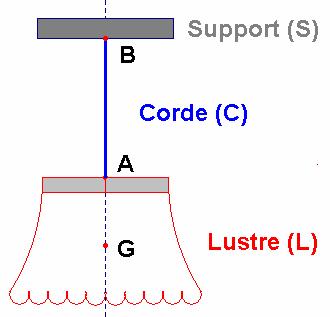
-  On considère un lustre de masse m = 500 g suspendu au plafond.

-  Quelles sont les actions mécaniques qu’il subit ?

-  Réponse :

-  On isole le lustre : on le représente seul.

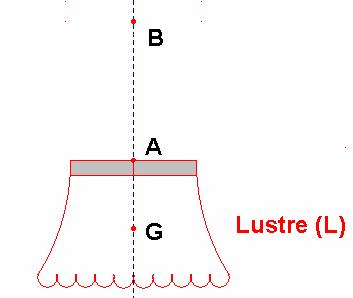
-  Le lustre est en interaction avec la Terre. Il est soumis à son poids . 

-  Le lustre est en interaction avec la corde, il est soumis à la force .

-  On peut donner les caractéristiques des différentes forces.

-  Caractéristiques du poids  du lustre :

-  Caractéristiques de la force .

-  Remarque :

-  On appelle tension d’une corde ou d’un fil, notée , la force exercée par une corde ou un fil sur un objet. 

-  En conséquence :  tension de la corde.

-  Pour aller plus loin : Le lustre est en équilibre, il est au repos. 

-  D’après la réciproque du principe de l’Inertie, le lustre est soumis à des forces dont les effets se compensent.

-  En conséquence :

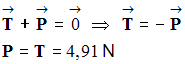
-  Représentation :

4)- Action mécanique exercée par un ressort. (TP Physique : étalonnage d’un ressort)

-  Un mobile autoporteur de masse m = 587g est posé sur une table plane et horizontale. 

-  Il est relié à un support fixe par l’intermédiaire d’un ressort (R) de raideur K

-  Au départ, le mobile autoporteur est à l’équilibre et le ressort est détendu. 

-  On écarte le mobile autoporteur de sa position d’équilibre et on le lâche à l’instant t = 0 s. 

-  Représenter le dispositif à l’instant t quelconque. 

-  Quelles sont les actions mécaniques que subit le mobile ? Le mobile peut-il être au repos ? Justifier.

-  Réponse : on isole le mobile autoporteur.

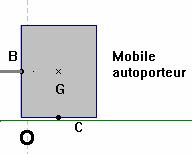
-  Le mobile autoporteur est en interaction avec la Terre  :

-  Il est en interaction avec le support (la table plane et horizontale) : réaction du support : .

-  Comme les frottements sont négligeables, elle est perpendiculaire au support.

-  Il est en interaction avec le ressort :  cette action est appelée tension du ressort. 

-  C’est une action localisée qui apparaît lorsque le ressort est étiré ou comprimé. 

-  Elle dépend de la raideur k du ressort et de l’allongement x du ressort.

-  Caractéristiques des différentes forces.

-  Représentation :

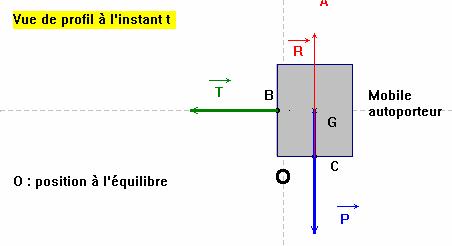
-  Si l’on fait la somme vectorielle des vecteurs forces appliqués au système, celle-ci est différente du vecteur nul : 

-  .

-  Le principe de l’inertie n’est pas respecté. Le système est en mouvement.

5)- Action d’un fluide sur un solide : La Poussée d’Archimède.

-  Que peut-on déduire de ces deux expériences ?

-  L’objet immergé est soumis de la part du fluide à une action mécanique.

La poussée d'Archimède : Tout corps immergé dans un fluide est soumis à une force verticale ,  orientée vers le haut, de valeur égale au poids du volume V de fluide déplacé par le corps immergé.

-  Caractéristiques de la Poussée d’Archimède.

-  Remarque : ρ₀ représente la masse volumique du fluide.

-  Pour l’eau : ρ₀  = 1,0 kg / dm ³.

-  Le centre de poussée C est situé au centre d’inertie du fluide déplacé.

-  Pour un solide homogène, C et G sont confondus.

-  Remarque :

-  La poussée d’Archimède exercée par un gaz sur un solide compact peut être négligée devant le poids d’un solide. 

-  C’est le cas d’une bille d’acier en mouvement dans l’air.

-  Cette approximation n’est pas possible dans le cas d’un liquide.

V- Les effets d’une force.

1)- Les effets dynamiques.

-  Une force est capable de modifier le mouvement d’un objet en mouvement.

-  Une force est capable de mettre en mouvement un objet initialement au repos.

2)- Les effets statiques.

-  Une force est capable de déformer un objet.

-  La déformation peut être élastique. L’objet reprend sa forme initiale lorsque cesse l’action. 

-  C’est le cas d’un ressort lorsque l’on ne dépasse pas sa limite d’élasticité.

-  La déformation peut être inélastique. C’est le cas d’un ressort que l’on a trop étiré.

-  Il ne reprend pas sa forme initiale. 

-  On a dépassé sa limite d’élasticité.

-  Une force est capable de maintenir un objet au repos en présence d’autres forces.

VI- Applications.

1)- QCM :

QCM : Force et mouvement dans le sport (Questy) Force et mouvement dans le sport (tableau) Force et mouvement dans le sport bis (Questy) Force et mouvement dans le sport bis (tableau) Révisions : lois et modèles (tableau) Révisions : lois et modèle (Questy)

2)- Exercices :