|
Modélisation de l’écoulement d’un fluide |
|
|
|
|
|
|
QCM N° 14
Modélisation de
l’écoulement d’un fluide
La Poussée
d’Archimède
La conservation
du débit volumique
La relation de
Bernoulli
Pour chaque
question, indiquer la (ou les) bonne(s) réponse(s). |
|||||
|
|
Énoncé |
A |
B |
C |
R |
|
1 |
La poussée
d’Archimède exercée sur un
corps immergé dans
un fluide est
due : |
Aux forces
pressantes
exercées par
le fluide |
Au poids
du corps
immergé |
À la forme
du corps
immergé |
A |
|
2 |
La poussée
d’Archimède : |
Est verticale |
Est orientée
vers le bas |
A une valeur
qui s’exprime
en newton |
AC |
|
3 |
La poussée
d’Archimède exercée sur un
houlographe de volume Vim immergé dans l’eau a pour
expression :
|
|
|
|
C |
|
4 |
Dans la station ISS, spationautes et objets sont en état d’"impesanteur". Les bulles d’une bouteille
d’eau gazeuse ouverte : |
Montent
à
la surface |
Restent sur
place |
Descendent au fond de la
bouteille |
B |
|
5 |
Le débit volumique DV d’un fluide qui traverse, pendant une durée Δt, la section S d’un tube avec une vitesse de valeur, v
a pour expression : |
|
|
|
B |
|
6 |
Le débit volumique se conserve systématiquement
pour : |
Un fluide
incompressible
en régime
permanent
indépendnat
du temps |
Un gaz
en régime
permanent
indépendnat
du temps |
Un liquide
en régime
permanent
indépendnat
du temps |
AC |
|
7 |
Un fluide incompressible, dont le débit volumique se conserve, a une vitesse
dont la valeur diminue :
|
Lorsque la
section S
du tube
qu’il
traverse
diminue. |
Lorsque la
section S
du tube
qu’il
traverse
augmente. |
Indépendamment
de la section
S
du tube
qu’il traverse |
B |
|
8 |
Dans la relation de Bernoulli :
|
ρ
s’exprime
en kg . L–1 ;
v
en m . s–1 ;
z
en m ;
P
en bar. |
Ρ
s’exprime
en kg . m–3 ;
v
en km .h–1 ;
z
en km ;
P
en bar. |
Ρ
s’exprime
en kg . m–3 ;
v
en m . s–1 ;
z
en m ;
P
en Pa. |
C |
|
9 |
Entre deux points A et B, la relation de Bernoulli s’écrit :
|
|
|
|
B |
|
10 |
D’après
ce
schéma à l’échelle,
on a :
|
PA
< PB |
PA
= PB |
PA
> PB |
A |
Origine de la poussée d’Archimède :
-
Dans un fluide au repos, la différence de
pression entre les parties inférieure et supérieure d’un solide immergé est à
l’origine de la poussée d’Archimède.
-
La résultante des forces pressantes exercées sur
un corps immergé dans un fluide incompressible au repos est appelée
poussée
d’Archimède.
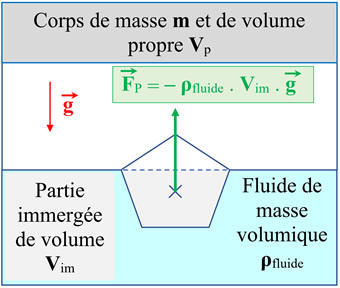
Expression vectorielle de la poussée d’Archimède.
-
La poussée d’Archimède
![]() exercée par un fluide de masse volumique
ρfluide est égale à l’opposé du poids du fluide déplacé.
exercée par un fluide de masse volumique
ρfluide est égale à l’opposé du poids du fluide déplacé.
-
Pour un corps ayant un volume immergé
Vim,
l’expression vectorielle est donnée par la relation suivante :
|
|
|
Point
d’application : centre de poussée C |
|
Direction :
verticale du lieu |
|
Sens : vers le
haut |
|
Valeur :
FP = ρfluide
. Vim . g
|
-
Schéma :
Valeur de la poussée d’Archimède :
|
FP
= ρfluide . Vim . g
|
FP :
Poussée d’Archimède en newton (N) |
|
ρfluide
: masse volumique du fluide au repos (kg . m–3) |
|
|
g :
intensité de la pesanteur (N . kg–1) |
|
|
Vim :
volume immergé du corps en mètre cube (m3) |
-
Remarque :
-
L’existence de la poussée d’Archimède est liée à
la présence du champ de pesanteur
![]() .
.
Régime permanent :
-
Un fluide s’écoule en régime permanent
indépendant du temps, si la valeur v de la vitesse en chaque position est
indépendante du temps t.
-
En régime permanent, la valeur
v de la
vitesse d’écoulement en tout point ne varie pas au cours du temps
t.

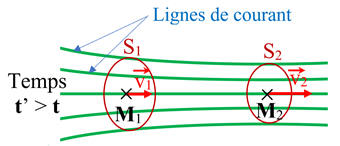
Débit volumique.
-
En régime permanent, le débit volumique
DV
d’un fluide correspond au volume V de fluide qui traverse une section
droite S pendant une durée
Δt.
-
Relation :
|
|
DV :
Débit volumique (m3 . s–1) |
|
V :
Volume de fluide (m3) |
|
|
Δt
: durée (s) |
-
Le débit volumique
DV est une
caractéristique de l’écoulement d’un fluide.
Débit volumique DV
:
- Le débit volumique DV est égal au produit de la surface S de la section de tube traversée par le fluide, par la valeur v de la vitesse du fluide au niveau de cette section.
- ρ s’exprime en kg . m−3 ; v en m . s−1 ; z en m ; P en Pa.
|
DV
= S . v |
DV :
Débit volumique (m3 . s–1) |
|
S :
surface de la section de tube traversée par le fluide (m2) |
|
|
v
: valeur de la vitesse du fluide au niveau de cette section (m . s–1) |
- Ne pas confondre la grandeur
V (m3)
qui représente le volume de fluide et la grandeur
v (m . s–1) qui représente
la vitesse d'éco
Conservation du débit volumique d’un fluide
incompressible :
-
Au cours d’un écoulement en régime permanent, le
débit volumique d’un fluide incompressible se conserve. Il ne varie pas.
-
Pour un fluide incompressible, le débit volumique
DV est le même en tout point du fluide.
-
Si la surface
S ↓ , de fluide, traversée
diminue, la valeur de la vitesse v ↑ d’écoulement du fluide augmente.
Relation de Bernoulli :
|
|
|
ρ :
masse volumique du fluide
(kg . m–3 ) |
|
P :
pression du fluide au point considéré (Pa) |
|
v
: vitesse du fluide au point considéré (m . s–1) |
|
g :
intensité de la pesanteur : g = 9,81 N. kg–1 |
|
z :
altitude au point considéré (m) |
|
Constante : (J
. m–3) |
►
La relation de Bernoulli :
-
Elle relie en toute position du fluide d’une même
ligne de courant :
-
La pression
P ;
-
La valeur de la vitesse
v ;
-
La coordonnée verticale
z de la position.
-
Pour une même ligne de courant :
-
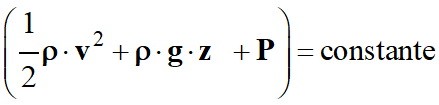
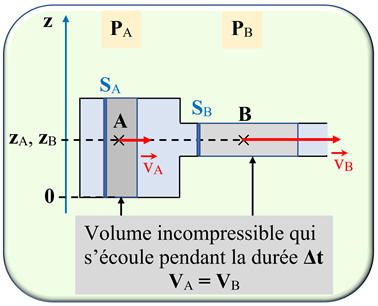
Effet Venturi :
-
La section de la surface
S se resserre :
SA >
SB
-
Comme le fluide est incompressible et que
l’écoulement s’effectue en régime permanent indépendant du temps, le débit
volumique est conservé :
-
DV =
DVA =
DVB
-
Les deux points
A et
B sont à la
même altitude :
-
zA =
zB
-
La relation de Bernoulli permet d’écrire que :
-
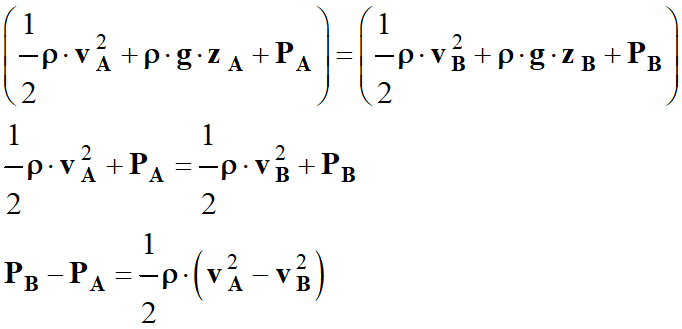
-
Alors :
-
vB >
vA =>
PB <
PA
-
Une valeur de la vitesse en
B supérieure à
la valeur de la vitesse en A, entraîne une pression plus petite en
B
qu’en A :
-
C’est l’effet Venturi.
|
|