|
|
Évolution d'un Exercices
|
|
|
|
|
|
QCM réalisé avec le
logiciel QUESTY
Pour
s’auto-évaluer
La
désintégration radioactive
La loi de
décroissance radioactive.
Applications et radioprotection. |
1)- Exercice 03 page 122 : Reconnaître les particules :
|
Reconnaître les particules :
A : nombre de masse Z :
nombre de charge
-
Particules et symboles : -
Autres particules importantes : -
Le proton :
-
Le neutron : |
2)- Exercice 05 page 122 : Utiliser les lois de conservations :
|
Utiliser les lois de conservations : 1.
Énoncer les lois de conservation à appliquer
pour établir l’équation d’une réaction nucléaire. 2. Recopier et compléter les équations de désintégration radioactives suivantes en déterminant A et Z. Nommer la particule émise. a.
b. c.
d.
|
|
Utiliser les lois de conservations : 1.
Lois de conservation à appliquer pour
établir l’équation d’une réaction nucléaire
-
Une réaction de désintégration
radioactive est modélisée par une équation.
-
Cette équation vérifie les lois de
conservation suivantes :
-
Conservation du nombre de charge Z.
-
Conservation du nombre de masse A.
-
-
Lois de Soddy :
-
Conservation du nombre de masse
A : A = A’ + a
-
Conservation du nombre de charge
Z : Z = Z’ + z 2.
Les équations de désintégration
radioactives. a.
-
Conservation du nombre de masse :
-
189
= 189 + A
=>
A = 0
-
Conservation du nombre de charge :
82 = 81 +
Z
=> Z = 1
-
La particule émise est un positon :
-
Équation de désintégration :
-
-
Noyau-père : le plomb 189
-
-
Noyau-fils : le thallium 189
-
-
Radioactivité
β+
(bêta plus) b.
-
Conservation du nombre de masse :
-
210
= A + 4
=>
A = 206
-
Conservation du nombre de charge :
90 =
Z + 2 =>
Z = 88
-
La particule émise est un noyau
d’hélium 4 :
-
Équation de désintégration :
-
-
Noyau-père : le thorium 210
-
-
Noyau-fils : le radium 206
-
-
Radioactivité
α (alpha) c.
-
Conservation du nombre de masse :
-
13
= 13 +
A =>
A = 0
-
Conservation du nombre de charge :
5 = 6 +
Z
=>
Z = – 1
-
La particule émise est un électron :
-
Équation de désintégration :
-
-
Noyau-père : le bore 13
-
-
Noyau-fils : le carbone 13
-
-
Radioactivité
β–
(bêta moins) d.
-
Conservation du nombre de masse :
-
A =
11 + 0 =>
A = 11
-
Conservation du nombre de charge :
Z
= 5 + 1 =>
Z = 6
-
La particule émise est un positon :
-
Équation de désintégration :
-
-
Noyau-père : le carbone 11
-
Noyau-fils : le bore 11
-
Radioactivité
β+
(bêta plus) |
3)- Exercice 07 page 122 : Écrire une équation de réaction nucléaire :
|
Écrire une équation de réaction nucléaire : Le polonium 211 est un noyau radioactif qui se désintègre en
émettant un noyau d’hélium 4.
-
Écrire l’équation associée à cette
désintégration radioactive.
-
Données :
-
Plomb
Pb (Z
= 82) ; Bismuth Bi (Z = 83) ;
-
Polonium
Po (Z
= 84) ; Astate At (
Z = 85) |
Écrire une équation de réaction nucléaire :
-
Le polonium 211 est un noyau
radioactif qui se désintègre en émettant un noyau d’hélium 4.
-
Une réaction de désintégration
radioactive est modélisée par une équation.
-
Cette équation vérifie les lois de
conservation suivantes :
-
Conservation du nombre de charge Z.
-
Conservation du nombre de masse A.
-
Radioactivité
α :
-
Dans le cas présent :
-
Le noyau-père : polonium 211 :
-
Le noyau-fils :
-
Le noyau-fils est le plomb 207 car Z
= 82
-
Équation associée à cette
désintégration radioactive :
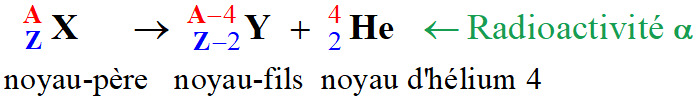
![]()
![]()
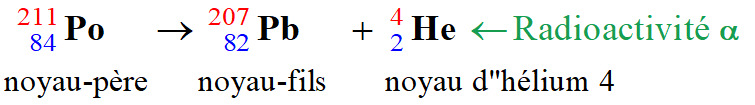
![]()
4)- Exercice 09 page 122 : Déterminer un type de radioactivité:
|
Déterminer un type de
radioactivité : Le phosphore 32 est radioactif et sa désintégration produit un
noyau de soufre 32. 1.
Établir l’équation de la réaction de
désintégration radioactive du phosphore 32. 2.
Identifier le type de radioactivité.
-
Données :
-
Phosphore
P (Z
= 15) ;
-
Soufre
S (Z
= 16). |
Déterminer un type de radioactivité
1.
Équation de la réaction de désintégration
radioactive du phosphore 32.
-
Une réaction de désintégration
radioactive est modélisée par une équation.
-
Cette équation vérifie les lois de
conservation suivantes :
-
Conservation du nombre de charge Z.
-
Conservation du nombre de masse A.
-
-
Lois de Soddy :
-
Conservation du nombre de masse
A : A = A’ + a
-
Conservation du nombre de charge
Z : Z = Z’ + z
►
Noyau-père : phosphore 32
-
A = 32 et Z = 15
-
Symbole du noyau :
►
Noyau-fils : Soufre 32
-
A = 32 et Z = 16
-
Symbole du noyau :
►
Équation de la réaction de désintégration
radioactive :
-
-
Conservation du nombre de masse :
-
32
= 32 +
A =>
A = 0
-
Conservation du nombre de charge :
-
15 = 16 +
Z
=>
Z = – 1
-
La particule émise est un électron :
-
Équation :
-
2.
Type de radioactivité.
-
Il s’agit de la radioactivité
β–
(bêta moins).
-
Le noyau-père possède trop de
neutrons :
-
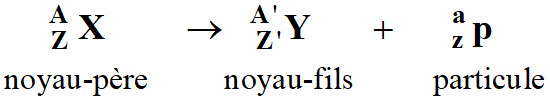
![]()
![]()
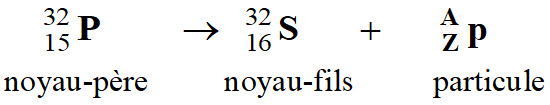
![]()
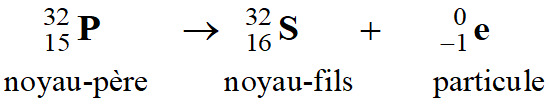

![]()
![]()
5)- Exercice 11 page 123 : Utiliser le diagramme (Z, N) :
|
Utiliser le diagramme (N,
Z) : - Préciser à partir de l’extrait du diagramme (N, Z) la stabilité ou l’instabilité des isotopes de l’aluminium,
en précisant le type de
radioactivité le cas échéant.
|
|
Utiliser le diagramme (N,
Z) :
-
L’aluminium 26 :
-
Isotope instable :
-
Il est émetteur β +:
-
La particule émise est un positon :
-
Radioactivité
β +:
-
L’aluminium 27 :
-
Isotope stable.
-
Abondance 100 %
-
L’aluminium 28 :
-
Isotope instable :
-
Il est émetteur β –:
-
La particule émise est un électron :
-
Radioactivité
β –: |
6)- Exercice 13 page 123 : Déterminer un nombre de noyaux radioactifs :
|
Déterminer un nombre de noyaux radioactifs : La courbe de décroissance radioactive d’un échantillon contenant
des noyaux radioactifs est fournie ci-dessous. 1.
Déterminer le nombre initial de noyaux
radioactifs dans l’échantillon. 2.
Déterminer le nombre de noyaux radioactifs
encore présents aux dates t = 5 s, 10 s, 15 s. 3.
Justifier que la demi-vie des noyaux
radioactifs est égale à 5 s. |
|
Déterminer un nombre de noyaux radioactifs : 1.
Nombre initial de noyaux radioactifs dans
l’échantillon.
-
Exploitation graphique : 2.
Nombre de noyaux radioactifs encore présents
aux dates t = 5 s, 10 s, 15 s.
-
Exploitation graphique :
3.
Demi-vie des noyaux radioactifs :
-
On remarque que :
-
t = 5 s alors
N =
N0 /2
-
t = 10 s alors
N =
N0 /4
-
t = 15 s alors
N =
N0 /8 - Pour un type de noyaux radioactifs, la demi-vie t1/2 est la durée au bout de laquelle la moitié
des noyaux radioactifs initialement présent dans l’échantillon se
sont désintégrés.
-
t1/2 ≈ 5 s |
7)- Exercice 15 page 123 : Calculer une durée :
|
Calculer une durée : Le tritium est contenu dans les résidus radioactifs issus de l’exploitation des centrales nucléaires. Sa constante radioactive de désintégration est égale à λ =
1,8 × 10–9 s–1.
1. Exprimer la durée t en fonction du nombre de noyaux radioactifs encore présents, de la constante de désintégration radioactive et du nombre de noyaux initialement présents. 2. Calculer cette durée en seconde puis en années pour que le nombre de noyaux radioactifs encore présents soit égal à 1 %
du nombre initial de noyaux. |
|
Calculer une durée : 1. Expression de la durée t en fonction du nombre de noyaux radioactifs encore présents, de la constante de désintégration radioactive et du nombre de noyaux initialement
présents.
-
L’évolution, au cours du temps, du
nombre N (t) de noyaux radioactifs d’un échantillon peut être modélisée par la loi
de décroissance radioactive :
-
λ est la constante de
désintégration (ou de décroissance) radioactive s –1.
-
-
Ou :
-
2.
Durée en seconde puis en années pour que le
nombre de noyaux radioactifs encore présents soit égal à 1 % du
nombre initial de noyaux.
-
Application numérique :
-
-
Demi-vie du tritium : -
-
Application numérique : -
-
Nombre n de demi-vie pour que le nombre de
noyaux radioactifs encore présents soit égal à 1 % du nombre initial de noyaux -
-
On considère que 99 % d’une population de noyaux
radioactifs est désintégrée après une durée de sept demi-vies environ.
|
||||||||||
8)- Exercice 17 page 124 : Déterminer une demi-vie :
|
Déterminer une demi-vie : La courbe de décroissance radioactive d’un échantillon de césium
137 est la suivante : 1.
Rappeler la définition de la demi-vie d’un
noyau radioactif. 2.
Déterminer graphiquement la demi-vie du
césium 137. 3.
En déduire la constante radioactive du
césium 137 en s–1. |
Déterminer une demi-vie : 1.
Définition de la demi-vie d’un noyau
radioactif.
-
Définition :
-
Pour un type de noyaux
radioactifs, la demi-vie t1/2 est la durée
au bout de laquelle la
moitié
des noyaux radioactifs initialement présent dans l’échantillon se
sont désintégrés. 2.
Détermination graphique de la demi-vie du
césium 137.
-
Graphe :
-
t1/2 ≈ 30 ans 3.
Constante radioactive du césium 137 en
s–1.
-
Relation entre t1/2
et λ :
-
-
-
Application numérique :
-
![]() ou
ou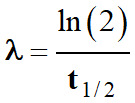
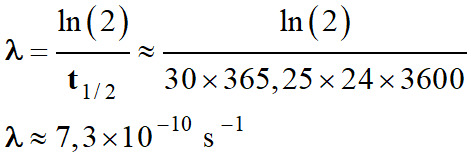
![]()
9)- Exercice 19 page 124 : Utiliser une activité :
|
Utiliser une activité : L’activité d’un échantillon d’un gramme de carbone d’une momie
égyptienne d’un pharaon a été évaluée en 2019 à 600,0 Bq. 1.
Écrire la loi vérifiée par l’activité d’un
échantillon en fonction du temps t. 2.
En déduire l’expression du temps t en
fonction de l’activité mesurée en 2019 et de la demi-vie du carbone
14. 3.
Estimer l’année de la mort du pharaon.
-
Données :
-
Activité d’un gramme de carbone 14
d’une matière vivante :
-
A0 = 816,0 Bq
-
Demi-vie du carbone 14 :
-
t1/2 = 5734
ans. |
Utiliser une activité : 1.
Loi vérifiée par l’activité d’un échantillon
en fonction du temps t.
-
La décroissance de
l’activité suit la même loi que la décroissance du nombre de noyau
radioactif d’un échantillon.
A (t) = A0
. exp ( – λ . t)
ou
A
(t) = A0
e – λ . t
A
(t)
Activité de l’échantillon radioactif à la date
t
A0
Activité de l’échantillon radioactif à la date
t0 = 0 s
λ
Constante radioactive (s –1)
t
Temps (s)
-
-
Or :
-
-
3.
Année de la mort du pharaon.
-
Application numérique :
-
-
Date
t’ du décès du pharaon :
-
t’ ≈ 2019 – 2544
-
t’ ≈ – 525 ans
-
Le pharaon est mort environ en – 525
ans av J.C.
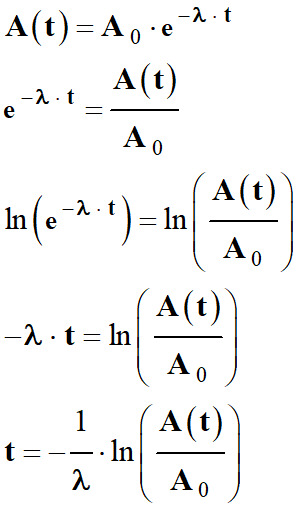
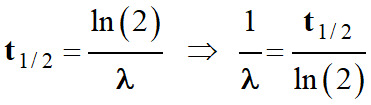
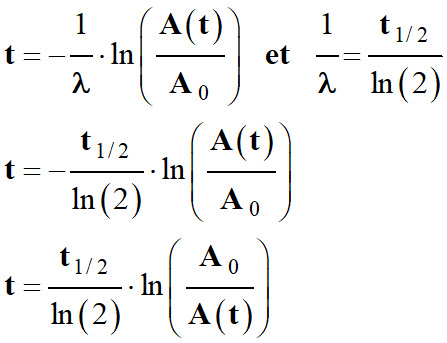
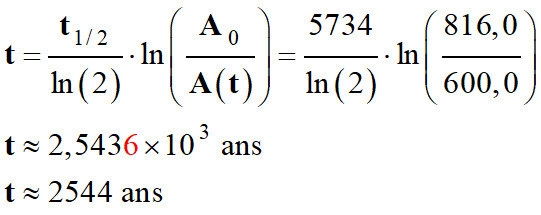
![]()
10)- Exercice 21 page 124 : Mesures de radioprotection pour une scintigraphie :
|
Mesures de radioprotection pour une scintigraphie : Le texte ci-dessous indique les mesures à prendre lors d’une
scintigraphie : « Les mesures de protection du personnel comportent l’utilisation de containers et de protège-seringues plombés. Ainsi que des gants lors de la préparation et de l’injection du radiopharmaceutique. L’utilisation d’écrans et de tabliers plombés lors de la
réalisation de l’examen sont préconisés ». D’après « la scintigraphie »,Société Française de
Médecine Nucléaire. 1.
Citer les méthodes utilisées pour se
protéger des rayonnements ionisants lors d’une scintigraphie. 2.
Citer une raison expliquant que le plomb est
un métal utilisé en radioprotection.
-
Données :
-
La CDA (couche de
demi-atténuation) est l’épaisseur d’une cible divisant par deux le flux de rayons gamma.
|
|
Mesures de radioprotection pour une scintigraphie : 1.
Méthodes utilisées pour se protéger des
rayonnements ionisants lors d’une scintigraphie.
-
« containers et de
protège-seringues plombés ».
-
Le produit radioactif, que l’on doit injecter, est
stocké dans des containers et des protège-seringues plombés.
-
« Gants, écrans et tabliers
plombés ».
-
Lors de l’injection, le manipulateur
porte des gants recouverts de plomb et il porte un tablier plombé ou manipule derrière un écran plombé. 2.
Utilisation du plomb en radioprotection.
-
Une source radioactive peut
émettre :
-
Des particules
-
Un rayonnement γ.
-
Les particules émises sont
de trois types : les particules α, β+et
β–.
-
Le rayonnement
α :
-
Ce rayonnement a un pouvoir de
pénétration très faible. - Il ne parcourt que quelques centimètres dans l’air. - Une feuille de papier ou les couches superficielles de la
peau l’arrêtent.
-
Rayonnements
β+et β– :
-
Ce rayonnement ne peut parcourir que
quelques mètres dans l’air.
-
Il est stoppé par une vitre ou une
feuille d’aluminium.
-
Rayonnement
γ :
-
Il parcourt dans l’air plusieurs
centaines de mètres.
-
Il faut des matériaux denses et épais
comme le béton (environ 2 m) et le plomb (plus de 20 cm) pour l’arrêter.
-
On utilise le plomb pour la
radioprotection car c’est le métal qui possède le coefficient d’atténuation le plus élevé.
-
Une épaisseur de 1,0 cm de plomb
atténue de moitié le flux du rayonnement
γ (gamma). |
11)- Exercice 23 page 125 : La découverte d’un élément radioactif :
|
La découverte d’un élément radioactif : Le polonium Po (Z = 84) a été isolé pour la première fois par Marie Curie en 1898. Le polonium 210 se désintègre en émettant une particule.
-
Extrait du diagramme (N,
Z) : 1.
Déterminer l’écriture conventionnelle du
polonium 210. 2.
Identifier la particule émise lors de la
désintégration du polonium 210, à l’aide du diagramme (N,
Z). 3.
Déterminer, à l’aide du diagramme (N,
Z) l’écriture conventionnelle du noyau-fils. 4.
Écrire l’équation de désintégration
radioactive. |
|
La découverte d’un élément radioactif :
-
Extrait du diagramme (N, Z) : (Nucleus Win)
-
Légende :
1.
Écriture conventionnelle du polonium 210.
-
Écriture conventionnelle d’un noyau :
-
avec
A : nombre de masse et
Z : nombre de charge.
-
Le polonium 210 :
Z = 84 et
A = 210
- 2.
Particule émise lors de la désintégration du
polonium 210, à l’aide du diagramme (N, Z).
-
Extrait du diagramme (N, Z) :
-
La particule émise est une particule
α : un noyau d’hélium 4.
- 3.
Écriture conventionnelle du noyau-fils.
-
Une réaction de désintégration
radioactive est modélisée par une équation.
-
Cette équation vérifie les lois de
conservation suivantes :
-
Conservation du nombre de charge Z.
-
Conservation du nombre de masse A.
-
Radioactivité
α :
-
-
Noyau-fils :
-
Nombre de masse :
A
– 4
-
Nombre de charge :
Z – 2
-
Nombre de neutrons :
A – Z – 2
-
Dans le diagramme (N, Z) :
-
Le noyau-père émet
un groupe de 4 nucléons
: 2 neutrons et 2 protons.
-
Le noyau-fils se trouve :
-
Deux lignes au-dessous du polonium
210
-
Et deux colonnes à gauche du polonium
210 :
-
Noyau de plomb : 4.
Équation de désintégration radioactive.
-
►
Capture électronique : EC
-
La capture électronique (en anglais
EC :
Electron Capture) est un
processus qui est en concurrence avec la désintégration
β+ .
-
Dans ce cas, un électron
e– d’une couche profonde de l'atome (en général de la
couche K) est absorbé
dans le noyau et un neutrino
ν est émis.
-
Un proton s’associe à un électron
pour former un neutron et émettre un neutrino.
-
-
Schématisation de la réaction :
-
|
|
|