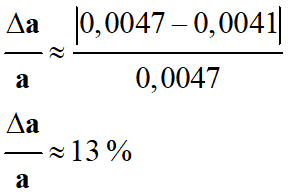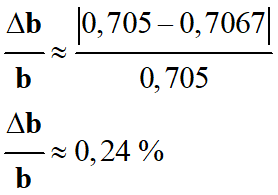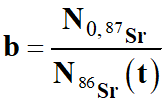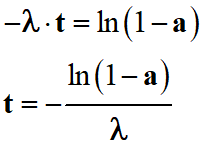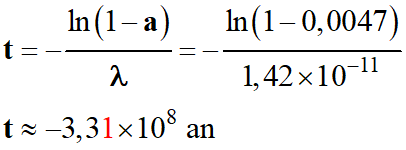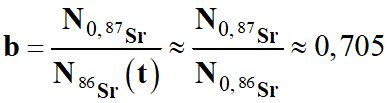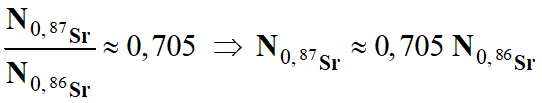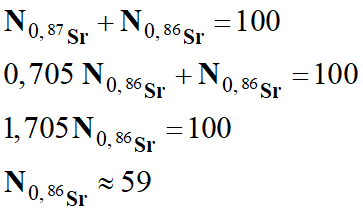Chap. N° 06 Exercices 2024 : Transfotmations nucléaires.
|
Chap. N° 06
|
Évolution d’un
système siège d’une
transformation nucléaire
Exercices 2024
Cours
Exercices
|
|
|
|
|
|
I-
Exercice : Identifier des isotopes naturels.
1)- Énoncé :
La méthode de datation « au potassium – argon » permet
de dater certaines roches.
DOC1 : Isotopes
du potassium
Le potassium (Z = 19) possède 3 isotopes naturels
dont les proportions en quantités de matières sont les suivantes :
39K (93,2581 %),
40K (0,001167 %) et 41K (6,7302 %)
Seul le potassium–40 est radioactif.
88 % des noyaux de potassium–40 se désintègrent en
40Ca (calcium–40) selon la réaction d’équation :
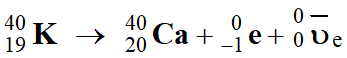 (réaction
1)
(réaction
1)
La constante radioactive associée à cette réaction de
désintégration est λ1 = 4,962 × 10-10 an-1,
ce qui donne une période radioactive soit un temps de
demi-réaction T1 = 1,40 Gan (milliard d’années).
12 %des noyaux de potassium-40 se désintègrent en
40Ar (argon-40) par capture d’une partie des électrons ainsi
produits (capture électronique).
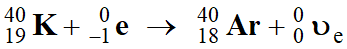 (réaction 2)
(réaction 2)
La constante radioactive associée à cette réaction de
transformation est λ2 = 0,581 × 10-10 an-1,
ce qui donne une période radioactive T2
= 11,9 Gan.
DOC2 : Extrait du
diagramme (N, Z)
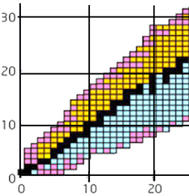
DONNÉE :
-
Le temps de demi-vie et la constante radioactive
sont liés par la relation suivante :
- 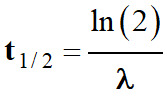
a)-
Expliquer en quoi l’équation de désintégration du potassium-40 en
calcium-40 caractérise une radioactivité β-.
b)-
Retrouver les valeurs du temps de demi-vie du potassium-40 associé aux
deux voies de désintégration.
c)-
Comparer les valeurs calculées dans la question précédente aux deux
périodes données dans le DOC1. Conclure
sur la signification de période radioactive.
d)-
Identifier les trois isotopes naturels du potassium sur le
DOC2 et reproduire les trois cases
correspondantes avec les couleurs adaptées.
e)-
Il existe un grand nombre d’autres isotopes du potassium. Expliquer
pourquoi le DOC1 ne les mentionne pas.

2)- Correction :
a)-
L’équation de désintégration du potassium-40 en calcium-40 caractérise
une radioactivité β-.
-
La radioactivité β- :
-
Les particules β–
(bêta moins) sont des électrons.
-
Symbole :
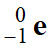
-
Masse : me = 9,1 × 10–31
kg
-
Charge : – e = – 1,60 × 10–19
C.
-
Les électrons sont émis à grande
vitesse v ≈ 2,8 × 108 m . s–1.
-
Ce sont des particules relativistes
(leur vitesse est voisine de celle de la lumière).
-
Elles sont plus pénétrantes mais moins ionisantes
que les particules α.
-
Elles sont arrêtées par un écran de
Plexiglas ou par une plaque d’aluminium de quelques centimètres.
-
Elles pénètrent la peau sur une
épaisseur de quelques millimètres.
-
Elles sont dangereuses pour la peau.
-
Les noyaux de potassium–40 se désintègrent en
40Ca (calcium–40) avec émission d’un électron.
-
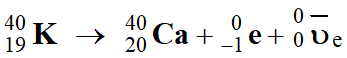 (réaction 1)
(réaction 1)
-
On constate aussi l’émission d’une autre
particule : l’antineutrino
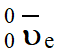
►
Additif :
-
En 1914, des mesures faites sur un grand nombre de
désintégrations β–, montrent que l’énergie cinétique acquise
par l’électron n’est qu’une fraction variable de l’énergie disponible.
-
En 1930, Wolfgang PAULI postule l’existence d’une
autre particule non détectée par les instruments de l’époque qui est émise lors
de cette désintégration.
-
Cette particule permet d’expliquer la conservation
de l’énergie et de la quantité de mouvement lors de cette transformation.
-
Cette particule neutre, de masse si faible (mν
< 0,23 eV/c2) que l’on ne peut pas la détecter, a été baptisée
neutrino (le petit neutre) par Enrico FERMI.
-
Écriture symbolique du neutrino :
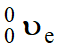
-
Le neutrino a été découvert expérimentalement en
1956, par Frederick Reines et Clyde Cowan, auprès d’un réacteur nucléaire.
-
Remarque :
-
L’antineutrino
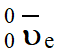 est l’antiparticule du neutrino
est l’antiparticule du neutrino
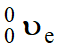 .
.
b)-
Valeurs du temps de demi-vie du potassium-40 associé aux deux voies de
désintégration.
-
Demi-vie t1/2.
-
Définition :
-
Pour un type de noyaux radioactifs, la
demi-vie t1/2 est la durée au bout de laquelle la moitié des
noyaux radioactifs initialement présent dans l’échantillon se sont désintégrés.
-
Relation entre t1/2
et λ :
-
Au temps t : N (t) = N
0 e – λ . t
-
Au temps t + t 1/2 :
-
N (t + t1/2
) = N 0 e – λ . (t + t1/2)
-
En conséquence :
-
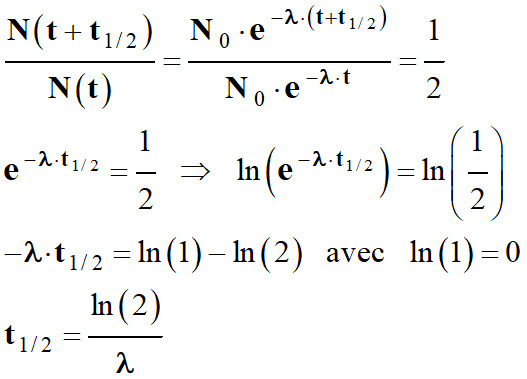
-
La demi-vie n’a qu’une valeur
statistique.
-
Elle indique qu’un noyau radioactif a une chance
sur deux de disparaître au bout d’une demi-vie.
c)-
Comparaison des valeurs calculées dans la question précédente aux deux
périodes données dans le DOC1.
-
Les valeurs : λ1 = 4,962 × 10-10
an-1 et λ2 = 0,581 × 10-10 an-1 :
-
Demi-vie pour la réaction 1 :
-
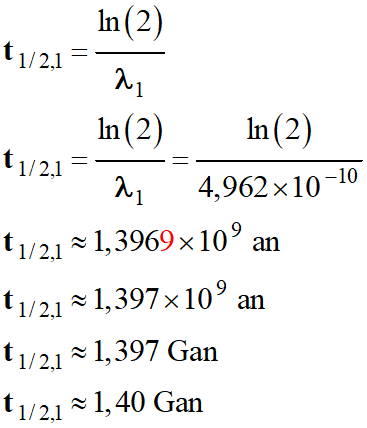
►
Préfixes décimaux :
-
La valeur t1/2,1 ≈ 1,397 Gan est
en accord avec T1 = 1,40 Gan
-
Demi-vie pour la réaction 2 :
-
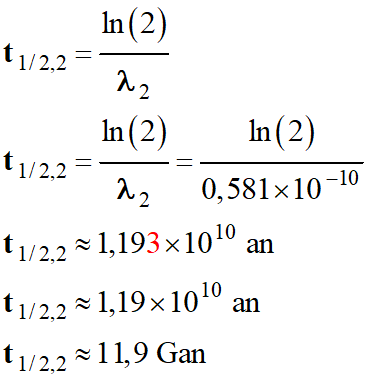
-
La valeur t1/2,2 ≈ 11,9 Gan est
en accord avec T2 = 11,9 Gan
-
Signification de période radioactive :
-
La période radioactive T d’un isotope
radioactif est aussi sa demi-vie t1/2.
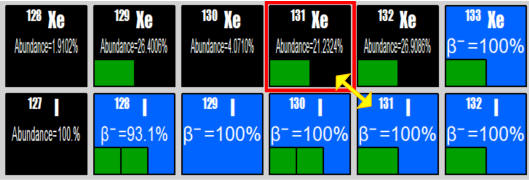
d)-
Identification des trois isotopes naturels du potassium sur le
DOC2.
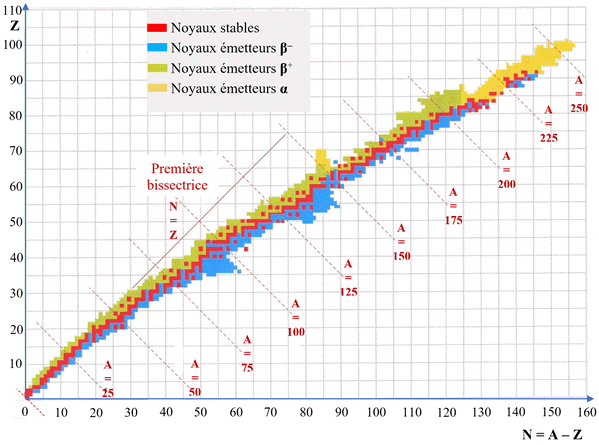
-
Diagramme (N, Z) :
-
Dans ce diagramme, on porte :
-
En abscisse, le nombre N de neutrons du
noyau
-
En ordonnée, le nombre Z de protons du
noyau.
-
Chaque isotope y est représenté par une case.
-
On retrouve sur une même ligne les isotopes d’un
même élément.
-
Exemple :
-
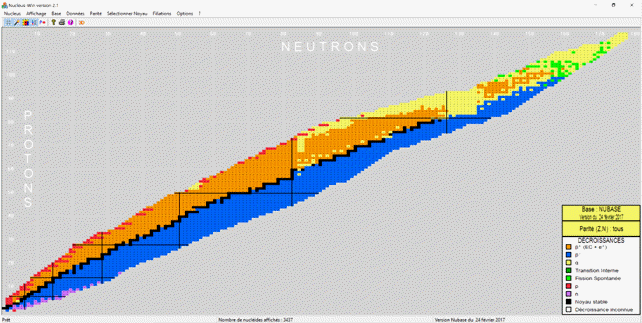
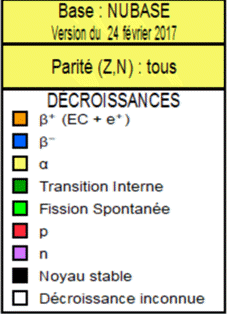
Le logiciel Nucleus Win :

-
Il permet d’obtenir des renseignements sur les
différents nucléides d’un élément chimique.
-
En noir les noyaux stables
-
En orange les noyaux instables émetteurs
β+
-
En bleu les noyaux instables émetteurs
β–
-
En jaune les noyaux instables émetteurs
α
-
Reproduction des trois cases correspondantes avec
les couleurs adaptées :
-
Avec l’application NUCLEUS-Win version2.1
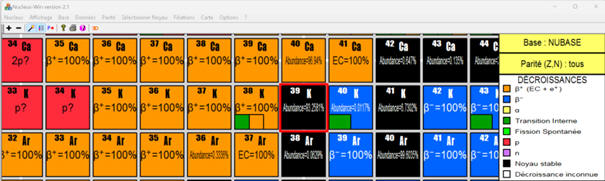
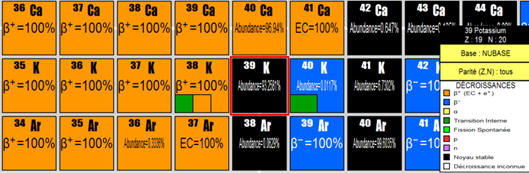
Les trois cases correspondantes des trois
isotopes naturels du potassium
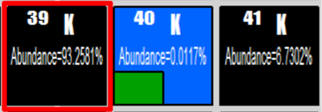
e)-
Il existe un grand nombre d’autres isotopes du potassium.
-
Le DOC1 ne
mentionne pas tous les isotopes du potassium.
-
Il ne mentionne que les isotopes naturels et il ne
traite pas des isotopes artificiels.
-
Le potassium possède 24 isotopes connus, dont la
majorité sont artificiels.
-
Les isotopes artificiels du potassium ont des
nombres de masse variant entre 32 et 56 ( ?).


-
Ces isotopes sont généralement produits dans des
réacteurs nucléaires ou des accélérateurs de particules et ont des demi-vies
très courtes, souvent inférieures à une journée.
-
Par exemple, les isotopes les plus légers, comme le
potassium-32, se désintègrent par émission de proton en isotopes de l’argon
Ar,
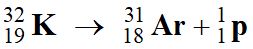
-
L’émission de proton est un type de désintégration
radioactive qui se produit dans les noyaux très déficients en neutrons (trop de
protons par rapport aux neutrons).
-
Les isotopes un peu plus lourds se désintègrent
principalement par désintégration β+ en isotopes de l’argon
Ar.
-
Les radioisotopes les plus lourds, y compris le
potassium-40, se désintègrent principalement par désintégration β−
en isotopes du calcium Ca.

II- Exercice : L’iode et la thyroïde.
1)- Énoncé.
L’apport d’iode est essentiel pour l’organisme humain.
La captation de cet élément par
l’organisme se fait sous la forme d’ion iodure au niveau de la glande thyroïde.
L’iode participe à la synthèse des hormones
thyroïdiennes.
En 2016 il a été décidé d'étendre le périmètre du plan
particulier d'intervention en étendant de 10 km à 20 km la zone d'application,
notamment avec la distribution de comprimés d'iode-127 (sous forme de d’iodure
de potassium KI) à prendre en cas de fuite radioactive d'iode-131.
DONNÉES :
-
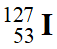 seul isotope naturel de l’iode, noyau non radioactif.
seul isotope naturel de l’iode, noyau non radioactif.
-
Iode-131 : isotope artificiel de l'iode, radioactif
β−, présent dans les rejets atmosphériques suite aux accidents
nucléaires et dans de nombreux examens médicaux.
-
Temps de demi-vie de l'iode-131 : t1/2
= 8,1 jours.
-
Constante d'Avogadro : NA = 6,02
× 1023 mol-1
a)-
Citer la zone du corps humain dans laquelle l’élément iode est capté.
b)-
Justifier la mesure consistant à prendre des pastilles d'iodure de
potassium en cas d'incident nucléaire.
c)-
Écrire l'équation de la désintégration de l'iode-131.
d)-
Définir le temps de demi-vie de l'iode-131.
e)-
Exprimer puis calculer λ, la constante radioactive de l'iode-131
f)-
Montrer que l'activité A d'un échantillon d'iode-131 de masse m
est donné par :
-
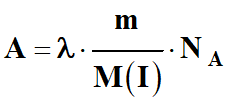
-
M (I) étant la
masse molaire de l’iode-131
g)-
Déduire de la réponse f)- la masse m1 d’iode-131
à injecter à un patient pour une scintigraphie thyroïdienne qui nécessite une
activité A1 = 37 MBq.
h)-
Construire, par une méthode de votre choix (table-grapheur, papier
millimétré, etc.) la représentation graphique de la décroissance de l'activité
du produit injecté au cours du temps, pour une durée comprise entre 0 et 50
jours.
i)-
Déduire de la réponse g)-, par une méthode graphique, la date t10
pour laquelle l'activité du produit injecté est divisée par 10.

2)- Correction.
Les isotopes de l'iode
a)-
Zone du corps humain dans laquelle l’élément iode est capté.
-
Énoncé : « La captation de cet élément par l’organisme se fait
sous la forme d’ion iodure au niveau de la glande thyroïde »
-
l’élément iode est capté au niveau de la glande
thyroïde.
b)-
Justification la mesure consistant à prendre des pastilles d'iodure de
potassium en cas d'incident nucléaire.
-
Lors d'un incident nucléaire, il est recommandé de
prendre des pastilles d'iodure de potassium pour protéger la glande thyroïde
contre l'absorption d'iode radioactif.
-
Un incident nucléaire peut produire une grande
quantité d’éléments radioactifs et en particulier de l’iode radioactif. L'iode
radioactif est un sous-produit de la fission nucléaire.
-
L'iode radioactif peut être libéré dans
l'environnement et être absorbé par la thyroïde, ce qui augmente le risque de
cancer de la thyroïde, surtout chez les enfants.
-
Les pastilles d'iodure de potassium satureront la
thyroïde avec de l'iode non radioactif (iode-127), empêchant ainsi l'iode
radioactif de s'y fixer et de causer des dommages.
-
L'iodure de potassium est un médicament qui
peut être utilisé pour protéger la glande thyroïde contre l'absorption de l'iode
radioactif en cas d'accident nucléaire.
-
Il est recommandé de prendre des comprimés d'iodure
de potassium en cas d'exposition à des radiations nucléaires, mais seulement sur
les conseils des autorités compétentes.
c)-
Équation de la désintégration de l'iode-131.
-
Iode-131 : isotope artificiel de l'iode, radioactif
β−, présent dans les rejets atmosphériques suite aux accidents
nucléaires et dans de nombreux examens médicaux.
-
La radioactivité β- :
-
Les particules β–
(bêta moins) sont des électrons.
-
Symbole :
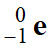
-
Masse : me = 9,1 × 10–31
kg
-
Charge : – e = – 1,60 × 10–19
C.
-
Les électrons sont émis à grande
vitesse v ≈ 2,8 × 108 m . s–1.
-
Ce sont des particules relativistes
(leur vitesse est voisine de celle de la lumière).
-
Elles sont plus pénétrantes mais moins ionisantes
que les particules α.
-
Elles sont arrêtées par un écran de
Plexiglas ou par une plaque d’aluminium de quelques centimètres.
-
Elles pénètrent la peau sur une
épaisseur de quelques millimètres.
-
Elles sont dangereuses pour la peau.
-
Équation de la désintégration :
-
Une réaction de désintégration radioactive est
modélisée par une équation.
-
Cette équation vérifie les lois de conservation
suivantes :
-
Conservation du nombre de charge Z.
-
Conservation du nombre de masse A.
-
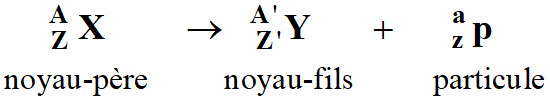
-
Lois de Soddy :
-
Conservation du nombre de masse A :
A = A’ + a
-
Conservation du nombre de charge Z : Z =
Z’ + z
-
En appliquant les lois de Soddy :
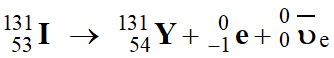
-
Comme pour le noyau-fils, Z = 54, la
classification périodique indique qu’on est en présence de l’élément Xénon de
symbole Xe.
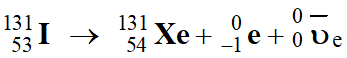
-
Les noyaux d’iode–131 se désintègrent en 131Xe
(xénon–131) avec émission d’un électron.
d)-
Définition du temps de demi-vie de l'iode-131.
-
Définition :
-
Pour un type de noyaux radioactifs, la
demi-vie t1/2 est la durée au bout de laquelle la moitié des
noyaux radioactifs initialement présent dans l’échantillon se sont désintégrés.
-
Relation entre t1/2
et λ :
-
Au temps t : N (t) = N
0 e – λ . t
-
Au temps t + t 1/2 :
-
N (t + t1/2
) = N 0 e – λ . (t + t1/2)
-
En conséquence :
-
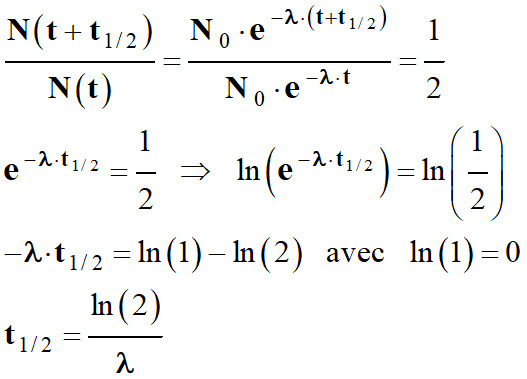
-
La demi-vie n’a qu’une valeur
statistique.
-
Elle indique qu’un noyau radioactif a
une chance sur deux de disparaître au bout d’une demi-vie.
e)-
Expression et calcul de λ, la constante radioactive de l'iode-131.
-
Chaque nucléide radioactif est caractérisé par une
constante de désintégration radioactive λ, qui est la probabilité de
désintégration d’un noyau par unité de temps.
-
Elle s’exprime en s–1.
-
La constante λ ne dépend que du nucléide.
-
Elle est indépendante du temps, des conditions
physiques et chimiques.
-
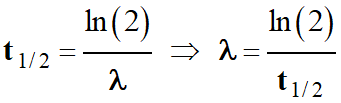
-
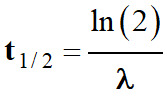
-
Application numérique :
-
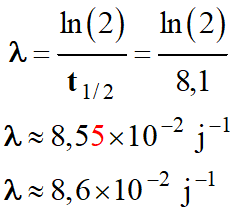
-
Ou :
-
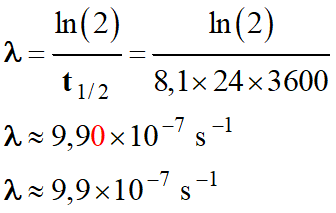
f)-
Activité A d'un échantillon d'iode-131 de masse m:
-
L’activité A (t) d’un échantillon
radioactif à la date t est le nombre de désintégrations par seconde de
cet échantillon.
-
L’unité d’activité est le Becquerel Bq en hommage à
Henri Becquerel.
-
1 Bq = 1 désintégration par seconde.
-
L’activité, à un instant donné, est égale à la
dérivée par rapport au temps de N (t).
-
N0 noyaux
radioactifs à la date t0.
-
N (t) noyaux
radioactifs à la date t.
-
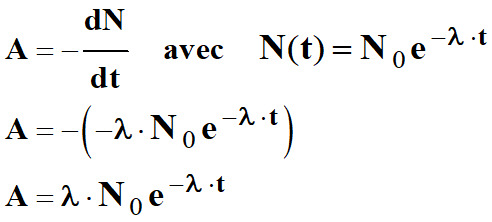
-
En conséquence :
-
A = λ . N
-
Avec N = n . NA
-
La grandeur NA représente le
nombre d’Avogadro.
-
La grandeur n représente la quantité de
matière de l’espèce chimique considérée :
-
Relation entre la quantité de matière n, la
masse m et la masse molaire M de l’espèce chimique
-
Dans le cas de l’iode :
-
m = n . M
(I)
-
On en déduit la relation suivante :
-
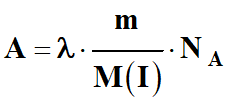
-
M (I) étant la
masse molaire de l’iode-131
g)-
Masse m1 d’iode-131 à injecter à un patient pour une
scintigraphie thyroïdienne qui nécessite une activité A1 = 37
MBq.
-
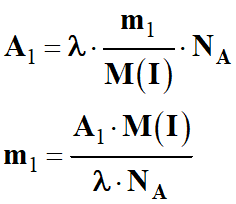
-
Application numérique :
-
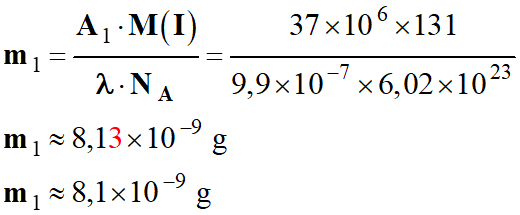
h)-
Représentation graphique de la décroissance de l'activité du produit
injecté au cours du temps.
-
Durée comprise entre 0 et 50 jours
-
La décroissance de l’activité suit la
même loi que la décroissance du nombre de noyau radioactif d’un échantillon.
|
A (t) = A0
. exp ( – λ . t)
ou
A
(t)
= A0
e – λ . t
|
|
A
(t)
|
Activité de
l’échantillon radioactif à la date t
|
|
A0
|
Activité de
l’échantillon radioactif à la date t0 = 0 s
|
|
λ
|
Constante
radioactive (s –1)
|
|
t
|
Temps (s)
|
-
Avec :
|
A (t) = A0
. exp ( – λ . t)
ou
A
(t)
= A0
e – λ . t
|
|
A
(t)
|
Activité de
l’échantillon radioactif à la date t
|
|
A0
|
Activité de
l’échantillon radioactif à la date t0 = 0 s
A0
= 37 MBq
|
|
λ
|
Constante
radioactive (j –1)
λ
= 8,6 × 10-2
j –1
|
|
t
|
Temps (j)
|
-
Comme on travaille sur une durée de 0 à 50 jours,
on peut prendre le jour comme unité.
-
Tableau de valeurs :
|
Temps
|
Activité
|
|
t
(j)
|
A
(MBq)
|
|
0
|
37,0
|
|
2
|
31,2
|
|
4
|
26,3
|
|
6
|
22,1
|
|
8
|
18,7
|
|
10
|
15,7
|
|
12
|
13,3
|
|
14
|
11,2
|
|
16
|
9,4
|
|
18
|
7,9
|
|
20
|
6,7
|
|
22
|
5,6
|
|
24
|
4,7
|
|
26
|
4,0
|
|
28
|
3,4
|
|
30
|
2,8
|
|
32
|
2,4
|
|
34
|
2,0
|
|
36
|
1,7
|
|
38
|
1,4
|
|
40
|
1,2
|
|
42
|
1,0
|
|
44
|
0,9
|
|
46
|
0,7
|
|
48
|
0,6
|
|
50
|
0,5
|
-
Représentation graphique : A = f (t)
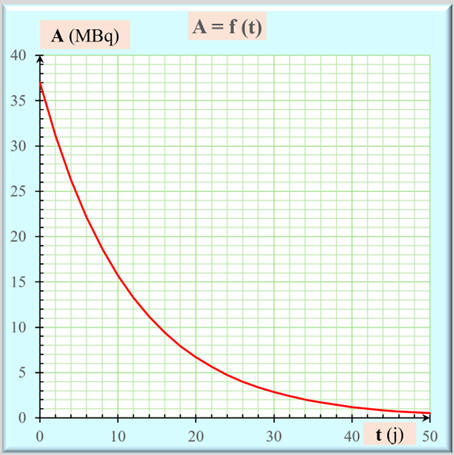
-
L’activité d’un échantillon radioactif est une
fonction décroissante du temps.
-
On parle de décroissance radioactive.
i)-
Date t10 pour laquelle l'activité du produit injecté
est divisée par 10.
-
Exploitation graphique :
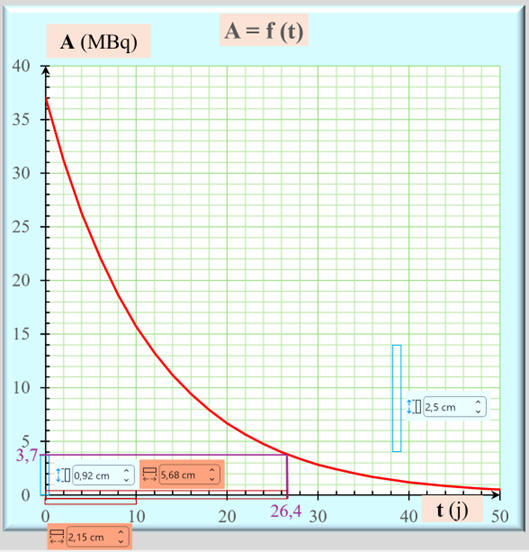
-
On peut faire une vérification :
-
Sachant que A (t10) = 3,7
MBq
-
A (t10)
= A0 e – λ . t10
-
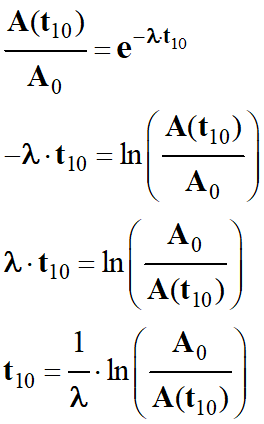
-
Pour simplifier :
- 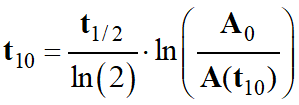
-
Avec :
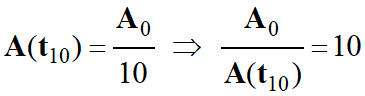
-
Application numérique :
-
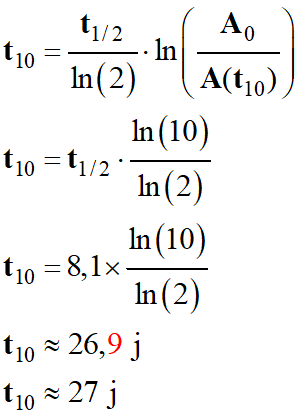
-
Les deux valeurs sont cohérentes.
-
Avec la représentation graphique on ne peut pas
avoir une grande précision.

III- Exercice : Le granit de Trégor.
1)- Énoncé.
Trégor est une ville bretonne sur la côte de granit
rose.
Lors de la formation de ces roches des noyaux
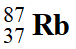 ,
,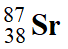 ,
,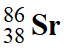 ont été
piégés dans un magma granitique.
ont été
piégés dans un magma granitique.
Le rubidium–87 est radioactifs
β–
(bêta moins) et sa désintégration conduit au strontium–87.
Si le système est isolé, la teneur isotopique en rubidium–87 diminue et celle en strontium–87 augmente, alors que celle en strontium–86
reste stable.
Grâce à un spectromètre de masse, six, échantillons de
granit sont analysés afin d’obtenir des rapports isotopiques qui permettent de
tracer la courbe isochrone, représentant le quotient
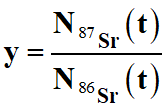 en fonction du quotient
en fonction du quotient
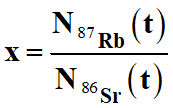 .
.
Les résultats des mesures sont donnés dans le tableau
suivant.
-
Tableau de mesures :
|
x
|
y
|
|
2,47
|
0,7167
|
|
0,209
|
0,7066
|
|
4,81
|
0,7278
|
|
5,52
|
0,7267
|
|
3,38
|
0,7229
|
|
1,54
|
0,7129
|
La datation des roches par la méthode rubidium-strontium
repose sur l'exploitation de la représentation graphique
x en fonction de
y ,appelée courbe isochrone.
Donnée :
-
Constante radioactive du rubidium-87 :
λ
= 1,42 × 10–11
an–1.
a)-
Écrire l'équation de désintégration du
rubidium–87.
b)-
Déduire de la loi de décroissance
radioactive la relation entre N87Rb (t),
le nombre de noyaux de rubidium-87 lors de l’analyse, et
N0,87Rb (t),
le nombre initial de noyaux de rubidium-87.
c)-
Justifier que :
N87Sr,
formés (t)
= N0,87Rb (t)
– N87Rb (t)
d)-
Déduire des réponses
b)-
et c)-, la relation :
N87Sr (t)
= N0,87Sr +
N0,87Rb ×
(1
–
e–
λ . t)
e)-
Démontrer la relation :
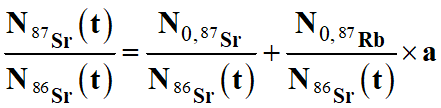
-
Avec
a
= (1
–
e–
λ . t)
f)-
Représenter la courbe isochrone par la
méthode de votre choix.
g)-
Modéliser la courbe obtenue par une
fonction affine et montrer que l'équation de cette fonction est :
-
y = 0,0047
x
+ 0,705.
h)-
Vérifier que l'âge des granits étudiés
est proche de 330 millions d’années.
i)-
Déterminer la valeur de la composition
initiale
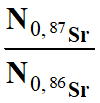 .
.
2)- Correction
a)-
Équation de désintégration du
rubidium–87.
-
La
radioactivité β– :
-
Les particules β–
(bêta moins) sont des électrons.
-
Symbole :
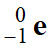
-
Masse : me
= 9,1 × 10–31 kg
-
Charge : – e
= – 1,60 × 10–19 C.
-
Cette équation vérifie
les lois de conservation suivantes :
-
Conservation du nombre
de charge Z.
-
Conservation du nombre
de masse A.
-
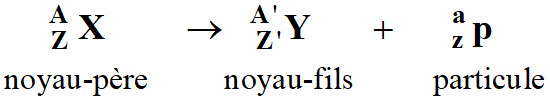
-
Lois de Soddy :
-
Conservation du nombre de masse
A :
A = A’ + a
-
Conservation du nombre de charge
Z :
Z = Z’ + z
-
En appliquant les lois
de Soddy :
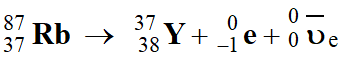
-
Comme pour le
noyau-fils, Z
= 38, la classification périodique indique qu’on est en présence de l’élément
strontium de symbole
Sr.
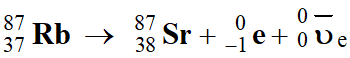 réaction 1
réaction 1
-
Les
noyaux de rubidium–87 se désintègrent en 87Sr
(strontium–87) avec émission d’un électron.
b)-
Relation entre
N87Rb (t),
le nombre de noyaux de rubidium-87 lors de
l’analyse, et N0,87Rb (t),
le nombre initial de noyaux de rubidium-87.
-
L’évolution, au cours
du temps, du nombre N
(t) de noyaux radioactifs d’un échantillon peut être modélisée par la loi
de décroissance radioactive :
|
N (t) = N0
. exp ( – λ . t)
ou
N
(t) = N0 e – λ . t
|
|
N
(t)
|
Nombre de
noyaux radioactifs présents à la date
t
|
|
N0
|
nombre de
noyaux présents à la date t0 = 0 s
|
|
λ
|
Constante
radioactive (s –1)
|
|
t
|
Temps (s)
|
-
λ
est la constante de désintégration (ou de décroissance) radioactive s
–1.
-
En utilisant les
notations de l’énoncé :
-
N87Rb (t)
= N0,87Rb e
– λ . t
c)-
Justification
que : N87Sr,
formés (t)
= N0,87Rb (t)
–
N87Rb (t)
-
N87Sr,
formés (t) :
représente le nombre de noyaux de strontium formé à l’instant
t.
-
Ces noyaux proviennent
de la désintégration des noyaux de rubidium-87
(réaction1).
-
À
l’instant t
=
t0 =
0, le nombre de noyaux radioactifs de rubidium-87 :
N0,87Rb
-
À
l’instant t,
le nombre de noyaux radioactifs de rubidium-87 est
alors : N87Rb (t)
-
Au cours du temps, on
observe une décroissance radioactive.
-
Le nombre de noyaux
radioactifs de rubidium-87 diminue
au cours du temps.
-
Le nombre de noyaux
radioactifs de rubidium-87 ayant
disparu à l’instant
t :
-
N87Rb,
disparus (t)
= N0,87Rb (t)
– N87Rb (t)
-
C’est aussi le nombre
de noyaux de strontium formé (voir la réaction1) :
-
N87Sr,
formés (t)
= N87Rb,
disparus (t)
= N0,87Rb (t)
– N87Rb (t)
d)-
Relation :
N87Sr (t)
= N0,87Sr +
N0,87Rb ×
(1 – e–
λ . t)
-
On
remplace N87Rb (t)
par son expression en fonction du temps
t :
-
N87Rb (t)
= N0,87Rb e
– λ . t
-
N87Sr,
formés (t)
= N0,87Rb (t)
–
N87Rb (t)
-
N87Sr,
formés (t)
= N0,87Rb (t)
–
N0,87Rb e
– λ . t
e)-
Démonstration de la
relation :
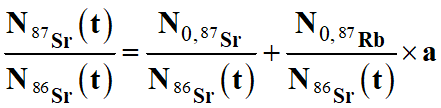
-
Avec
a
= (1
–
e–
λ . t)
-
Pour
obtenir cette relation, il faut diviser chaque terme de la relation précédente
par N86Sr.
-
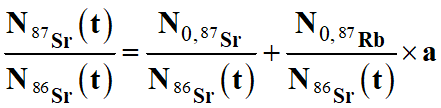
-
Avec :
a
= (1
–
e–
λ . t)
f)-
Représentation de la courbe
isochrone.
-
Tableau de valeurs :
|
x
|
y
|
|
2,47
|
0,7167
|
|
0,209
|
0,7066
|
|
4,81
|
0,7278
|
|
5,52
|
0,7267
|
|
3,38
|
0,7229
|
|
1,54
|
0,7129
|
-
Représentation
graphique :
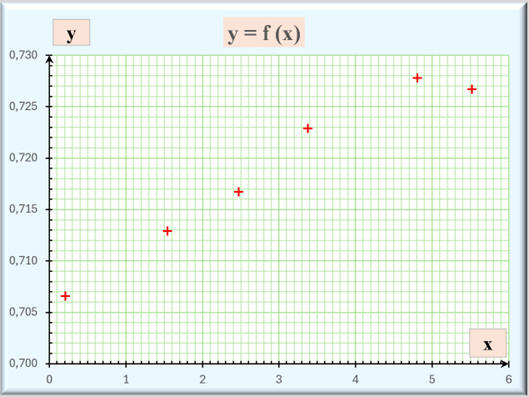
-
L’origine des
ordonnées a été choisie à 0,700 pour plus de lisibilité.
g)-
Modélisation et équation de
la courbe obtenue :
-
Pour la modélisation,
on peut tracer la droite moyenne :
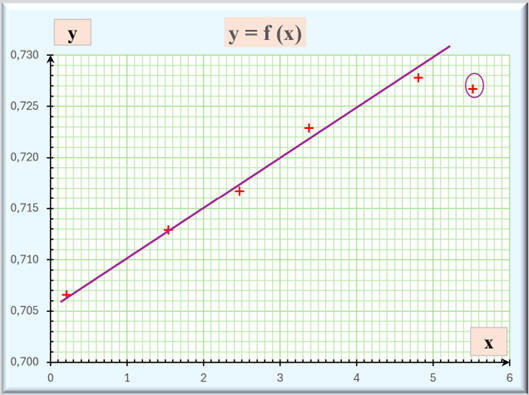
-
La valeur (5,52 ;
0,7267) s’écarte
sensiblement de la droite moyenne tracée.
-
Dans un premier temps,
on peut écarter cette valeur et réaliser une étude statistique avec un tableur :
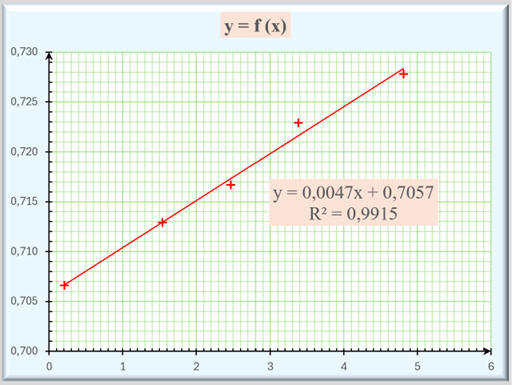
-
Équation de la droite
de régression :
-
y
≈ 0,0047 x
+ 0,7057 avec un coefficient de détermination :
R2
≈ 0,9915
-
Le coefficient de
détermination est proche de 1.
-
L’adéquation entre les grandeurs
x et
y est bonne.
-
Ce résultat est en
accord avec l’équation proposée dans l’énoncé.
-
y
= 0,0047 x
+ 0,705.
-
Dans un second temps,
on tient compte de toutes les valeurs :
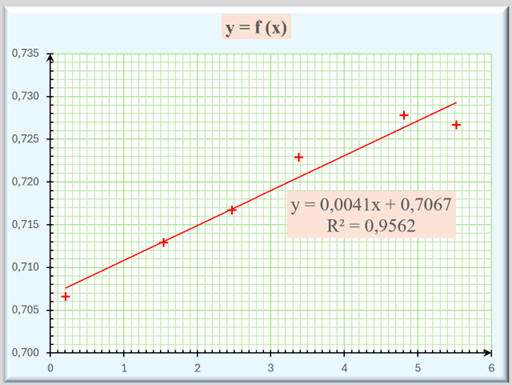
-
Équation de la droite
de régression :
-
y
≈ 0,0041 x
+ 0,7067 avec un coefficient de détermination :
R2
≈ 0,9562
-
Le coefficient de
détermination n’est pas trop proche de 1.
-
L’adéquation entre les grandeurs
x et
y est bonne médiocre dans ce
cas.
-
La
fonction affine est du type :
y =
a . x +
b
-
Incertitude relative sur la grandeur
a :
-
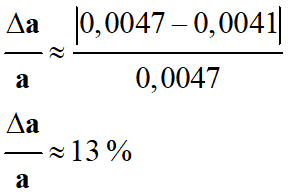
-
Incertitude relative sur la grandeur
b :
-
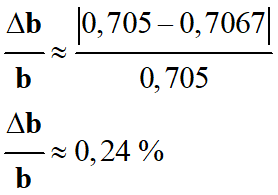
h)-
Vérification de l'âge des
granits étudiés.
-
Par identification
entre les deux relations :
-
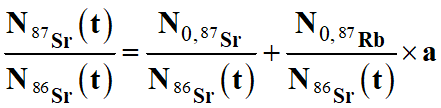 et
y
= a . x
+ b
et
y
= a . x
+ b
-
Avec :
-
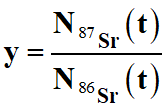 et
et
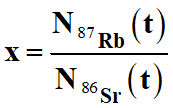
- 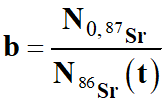 et
a
= (1
–
e–
λ . t)
et
a
= (1
–
e–
λ . t)
-
a
= (1
-
e–
λ . t) = 0,0047
-
1
–
a
=
e–
λ . t
-
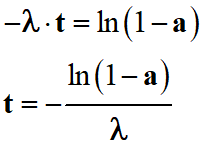
-
Application
numérique :
-
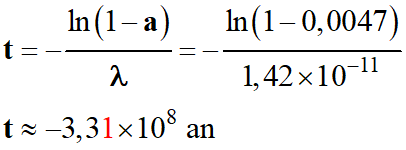
-
t
≈ 3,3 × 108 an
-
t
≈ 330 × 106 an
-
L’âge des granits
étudiés est proche de 330 millions d’années.
i)-
Détermination de la valeur de
la composition initiale
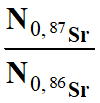 .
.
-
Le rubidium–87
est radioactifs β–
(bêta moins) et sa désintégration conduit au
strontium–87.
-
Si le système est
isolé, la teneur isotopique en rubidium–87 diminue et celle en strontium–87 augmente, alors que celle
en strontium-86
reste stable.
-
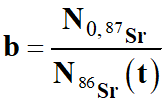
-
Comme la teneur en
strontium-86
reste stable au cours du temps,
on peut considérer que :
-
N86Sr (t)
≈ N0,86Sr
- 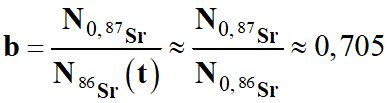
-
Pour effectuer
le calcul, on considère 100 noyaux de strontium à l’instant initial :
-
N0,87Sr +
N0,86Sr =
100
-
D’autre part :
-
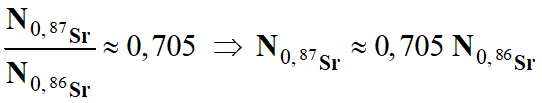
-
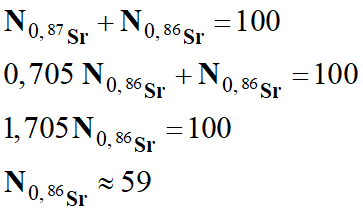
-
On en déduit la valeur
suivante :
-
N0,87Sr ≈
41
-
Au départ, il y a
environ 59 % de strontium-86
et 41 % de strontium-87.
![]() (réaction
1)
(réaction
1)![]() (réaction 2)
(réaction 2)
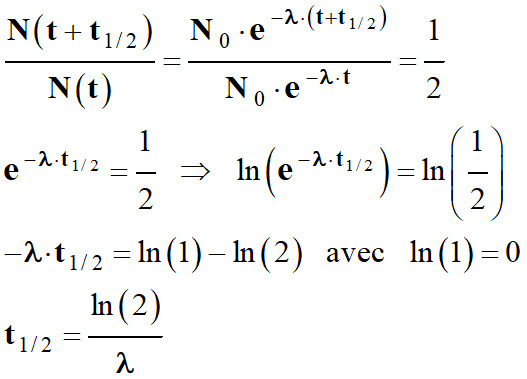
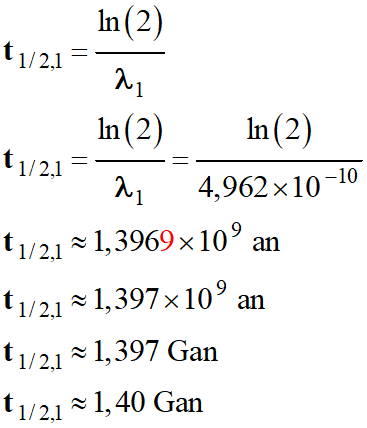
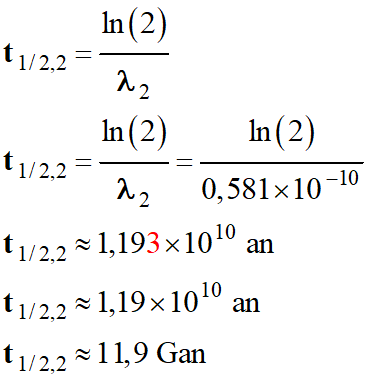






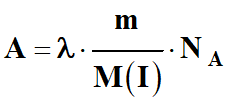
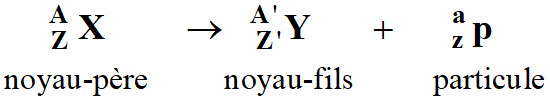

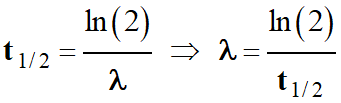
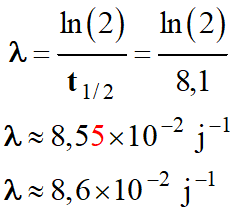
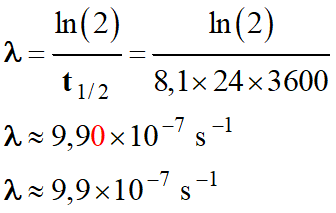
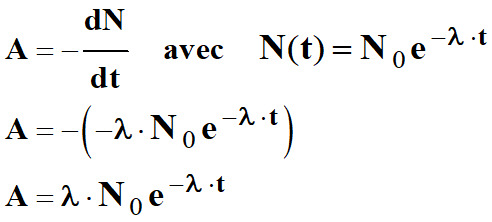
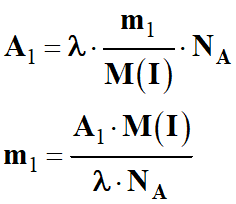
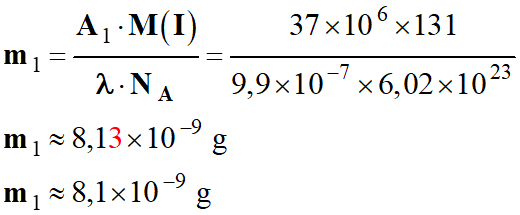


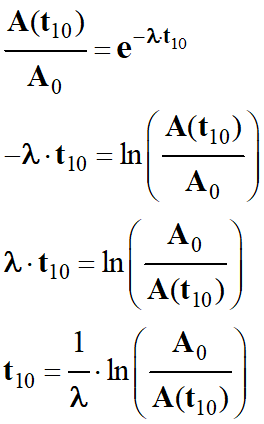
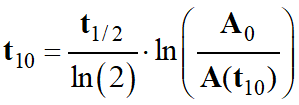
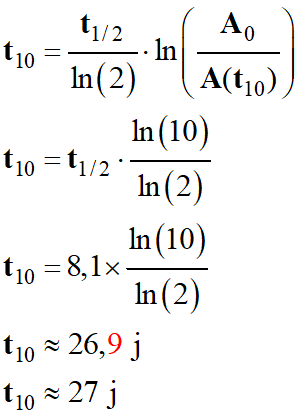
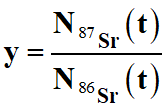 en fonction du quotient
en fonction du quotient
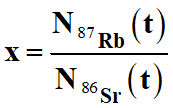 .
.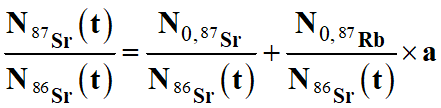
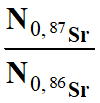 .
.