I- La désintégration radioactive.

1)- Introduction.

-  La radioactivité a été découverte par Henri BECQUEREL en 1896 (1852 – 1908).

-  Il découvre la radioactivité de l’uranium au cours de travaux sur la phosphorescence.

-  Les travaux sont poursuivis par Pierre et Marie CURIE.

-  En 1898, ils découvrent la radioactivité du polonium 210 (Polonium) et du radium 226 (Radium).

-  En 1903 : prix Nobel de physique (Henri BECQUEREL avec Pierre et Marie CURIE).

-  La radioactivité artificielle fut mise en évidence en 1934 par Irène et Frédéric JOLIOT – CURIE.

-  Ils ont créé par réaction nucléaire un isotope radioactif du phosphore.

-  Ils bombardent une feuille d’aluminium avec des particules α.

-  On connaît actuellement, une cinquantaine de nucléides naturels radioactifs et environ 3000 nucléides artificiels radioactifs.

-  La radioactivité est un phénomène physique naturel, aléatoire et spontané, qui concerne certains noyaux.

2)- Stabilité d’un noyau.

-  La cohésion du noyau est due à l’existence d’une interaction forte, attractive qui unit l’ensemble des nucléons et qui prédomine devant l’interaction électrique (répulsion entre les protons).

-  Il y a antagonisme entre l’interaction forte et la répulsion des protons.

-  Dans certains cas la cohésion n’est pas suffisante, on dit que les noyaux sont instables.

-  Un noyau est instable s’il possède trop de protons par rapport au nombre de neutrons.

-  Un noyau est instable s’il possède trop de neutrons par rapport au nombre de protons.

-  Un noyau est instable s’il possède trop de protons et trop de neutrons (trop de nucléons).

-  Ils se désintègrent spontanément, on dit qu’ils sont radioactifs.

-  Ce sont des radionucléides.

3)- Radioactivité α, β⁺ et β^–.

-  Une source radioactive peut émettre :

-  Des particules

-  Un rayonnement γ.

-  Les particules émises sont de trois types : les particules α, β⁺et β^–.

►  Les particules α (alpha).

-  Ce sont des particules positives, des noyaux d’hélium dont l’écriture symbolique :

-  , ion He²⁺.

-  Ces particules sont éjectées à grande vitesse v ≈ 2 × 10⁷ m . s^–1.

-  Ce ne sont pas des particules relativistes.

-  Les particules sont directement ionisantes mais peu pénétrantes.

-  Elles sont arrêtées par une feuille de papier et par une épaisseur de quelques centimètres d’air.

-  elles pénètrent la peau sur une épaisseur de l’ordre de quelques micromètres.

-  Elles ne sont pas dangereuses pour la peau.

-  En revanche, elles sont dangereuses par absorption interne : inhalation, ingestion.

►  Les particules β (bêta).

-  On distingue :

-  Les particules β^– (bêta moins) qui sont des électrons :

-  Symbole :

-  Masse : m_e = 9,1 × 10^–31 kg

-  Charge : - e = – 1,60 × 10^–19 C.

-  Les particules β⁺ (bêta plus) qui sont des positons (antiparticule de l’électron).

-  Symbole :

-  Masse : m_e = 9,1 × 10^–31 kg

-  Charge : e = 1,60 × 10^–19 C.

-  Les particules sont émises à grande vitesse v ≈ 2,8 × 10⁸ m . s^–1.

-  Ce sont des particules relativistes (leur vitesse est voisine de celle de la lumière).

-  Elles sont plus pénétrantes mais moins ionisantes que les particules α.

-  Elles sont arrêtées par un écran de Plexiglas ou par une plaque d’aluminium de quelques centimètres.

-  Elles pénètrent la peau sur une épaisseur de quelques millimètres.

-  Elles sont dangereuses pour la peau.

►  Le rayonnement γ (gamma).

-  Il accompagne l’émission de particules α, β⁺et β^–.

-  Il est constitué d’une onde électromagnétique de très courte longueur d’onde

-  (λ ≈ 10^–12 m et υ ≈ 10 ²⁰ Hz).

-  Le rayonnement est constitué de photons qui se déplacent à la vitesse de la lumière et dont la masse est nulle.

-  Ils ne sont pas directement ionisants, mais ils sont très pénétrants.

-  Ils peuvent traverser jusqu’à 20 cm de plomb.

-  Par interaction avec les atomes des substances traversées, ils peuvent donner naissance à des électrons qui eux sont ionisants.

Conclusion :

-  Au cours d’une désintégration radioactive, un noyau instable se transforme spontanément en un noyau d’un autre élément chimique.

-  Cette désintégration s’accompagne de l’émission d’une particule et d’un rayonnement gamma.

-  Le noyau qui se désintègre est appelé :

-  le noyau-père:

-  et le noyau formé est appelé :

-  Le noyau-fils,

-  Il existe trois types de radioactivité, caractérisés par la particule émise lors de la désintégration du noyau radioactif :

-  Tableau :

-  Une particule, α, β⁺ou β^–,

4)- Équation de réaction de désintégration nucléaire.

-  Une réaction de désintégration radioactive est modélisée par une équation.

-  Cette équation vérifie les lois de conservation suivantes :

-  Conservation du nombre de charge Z.

-  Conservation du nombre de masse A.

-   

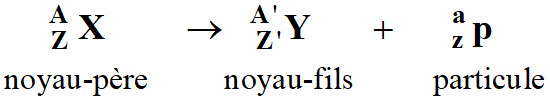
-  Lois de Soddy :

-  Conservation du nombre de masse A : A = A’ + a

-  Conservation du nombre de charge Z : Z = Z’ + z

►  Remarque :

-  Lors d’une réaction nucléaire, il n’y a pas conservation des éléments chimiques.

-  Dans les équations de réactions nucléaires, on écrit uniquement les particules possédant une charge ou une masse.

-  Les rayonnements gamma n’apparaissent pas.

-  Les trois types de radioactivité :

►  Exemples :

►  Radioactivité α :

-  Un noyau lourd instable éjecte une particule α et donne un noyau-fils plus léger, généralement dans un état excité.

-  L’uranium 238 est émetteur α.

-  Écrire l’équation de la réaction.

►  Radioactivité β^– :

-  Cette radioactivité se manifeste lorsque le noyau présente un excès de neutrons.

-  Le césium 137 est émetteur β^–.

-  Écrire l’équation de la réaction.

-  Le noyau-père possède trop de neutrons :

►  Radioactivité β⁺ :

-  Cette radioactivité se manifeste lorsque le noyau d’un atome possède trop de protons.

-  Au cours de la désintégration, il y a émission d’un positon noté .

-  L’oxygène 14 est émetteur β⁺.

-  Écrire l’équation de la réaction.

-  Le noyau-père possède trop protons :

5)- Diagramme (N, Z).

-  Pour un élément chimique donné, certains isotopes sont stables tandis que d’autres ne le sont pas.

-  Il sont donc radioactifs.

-  Le diagramme (N, Z) indique les isotopes stables ou radioactifs.

-  Il donne aussi le type d’émission radioactive des isotopes instables.

-  Dans ce diagramme, on porte :

-  En abscisse, le nombre N de neutrons du noyau

-  En ordonnée, le nombre de protons du noyau.

-  Chaque isotope y est  représenté par une case.

-  On retrouve sur une même ligne les isotopes d’un même élément.

-  L’ensemble des noyaux stables (en rouge) forme sur la représentation graphique la vallée de stabilité.

-  Les noyaux légers stables ont une tendance à la symétrie.

-  Ils se répartissent au voisinage de la première bissectrice (N = Z autant de protons que de neutrons).

-  Les noyaux lourds stables s’écartent de la bissectrice. Ils ont plus de neutrons que de protons.

-  Pour les noyaux instables :

-  En bout de la vallée de stabilité, ils se désintègrent en émettant des particules alpha : ils sont radioactifs alpha.

-  Au-dessous de la vallée de stabilité, ils sont émetteurs β^–. 

-  Au-dessus du domaine de stabilité, ils sont émetteurs β⁺. 

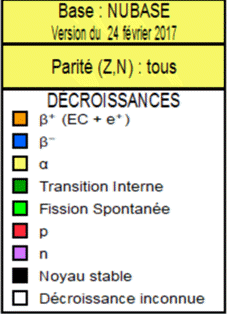
-  Tableau réduit :

-  Légende :

-  Le logiciel Nucleus Win :

-  Il permet d’obtenir des renseignements sur les différents nucléides d’un élément chimique.

-  En noir les noyaux stables

-  En orange les noyaux instables émetteurs β⁺

-  En bleu les noyaux instables émetteurs β^–

-  En jaune les noyaux instables émetteurs α

-  Cas de l’élément oxygène :

-  L'oxygène possède 17 isotopes connus de nombre de masse variant de 12 à 28.

-  Les isotopes les plus stables sont : ¹⁶O, ¹⁷O et ¹⁸O,

-  ¹⁶O est ultra-majoritaire dans la nature (plus de 99,76 % de l'oxygène naturel).

-  L'oxygène naturel est constitué des trois isotopes stables.

-  ¹²O est un isotope très instable. C’est un nucléide émetteur de proton.

-  L’émission d’un proton est aussi un type de désintégration radioactive.

-  De même, ²⁵O est un nucléide émetteur de neutron (autre type de désintégration radioactive).

-  Il donne un isotope avec un neutron de moins.

-  Quelques nucléides de l’oxygène :

-  Les noyaux émetteurs β⁺

-  Les noyaux stables avec l’abondance :

-  Les noyaux émetteurs β^–

II- Loi de décroissance radioactive.

1)- Caractère aléatoire d’une désintégration radioactive.

-  Un noyau instable est susceptible de revenir à l’état stable à tout moment.

-  Le phénomène de désintégration est imprévisible.

-  Pour un noyau instable donné, on ne peut prévoir la date de sa désintégration.

-  En revanche, on connaît la probabilité de désintégration de ce noyau par unité de temps.

-  Le phénomène de désintégration est aléatoire.

-  La probabilité qu’a un noyau radioactif de se désintégrer pendant une durée donnée est indépendante de son âge.

-  Elle ne dépend que du type de noyaux considéré.

-  Un noyau de carbone 14 apparu, il y a mille ans et un autre formé, il y a 5 min ont exactement la même probabilité de se désintégrer dans l’heure qui vient.

-  Un noyau ne vieillit pas.

-  Ce caractère aléatoire fait que pour un ensemble de noyaux instables identiques, on ne peut prévoir lesquels seront désintégrés à une date donnée, mais on peut prévoir combien de noyaux seront désintégrés.

-  On peut prévoir avec précision l’évolution statistique d’un grand nombre de noyaux radioactifs.

-  C’est un phénomène sur lequel il est impossible d’agir.

-  Il n’existe aucun facteur permettant de modifier les caractéristiques de la désintégration d’un noyau radioactif.

2)- La constante radioactive λ.

-  Chaque nucléide radioactif est caractérisé par une constante de désintégration radioactive λ, qui est la probabilité de désintégration d’un noyau par unité de temps.

-  Elle s’exprime en s^–1.

-  La constante λ ne dépend que du nucléide.

-  Elle est indépendante du temps, des conditions physiques et chimiques.

-  Pendant la durée Δt,

-  la probabilité, pour qu’un noyau se désintègre, est :  λ . Δt.

3)- Loi de décroissance radioactive.

-  Considérons un échantillon contenant :

-  N₀ noyaux radioactifs à la date t₀.

-  N (t) noyaux radioactifs à la date t.

-  A la date t + Δt très proche de t, le nombre de noyaux radioactifs a diminué.

-  Pendant l’intervalle de temps Δt très court, on peut considérer que le nombre de noyaux ayant subi une désintégration est :  λ . Δt . N.

-  ΔN (t)  = N (t) – N₀ < 0

-  La variation ΔN du nombre N de noyaux pendant la durée Δt est donnée par la relation :

-  ΔN (t)  = – λ . Δt . N (t)  soit :

-  ΔN (t)  +  λ . Δt . N (t)  = 0  (1) 

-  Divisons l’expression (1) par Δt, il vient :

-   

-  Lorsque Δt → 0, l’expression (2) s’écrit :

- 

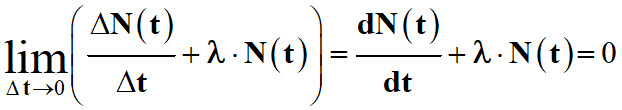
-  La grandeur  représente la dérivée de N (t) par rapport au temps t.

-   

-  On est en présence d’une équation différentielle du premier ordre sans second membre.

-  La solution de cette équation différentielle du premier ordre donne la loi de décroissance radioactive :

-  L’évolution, au cours du temps, du nombre N (t) de noyaux radioactifs d’un échantillon peut être modélisée par la loi de décroissance radioactive :

-  λ est la constante de désintégration (ou de décroissance) radioactive s^–1.

4)- Demi-vie t_1/2.

-  Définition :

-  Pour un type de noyaux radioactifs, la demi-vie t_1/2 est la durée au bout de laquelle la moitié des noyaux radioactifs initialement présent dans l’échantillon se sont désintégrés.

-  Relation entre t_1/2 et λ :

-  Au temps t : N (t) = N ₀ e ^{– λ . t}

-  Au temps t + t _1/2 :

- 

-  En conséquence : 

-   

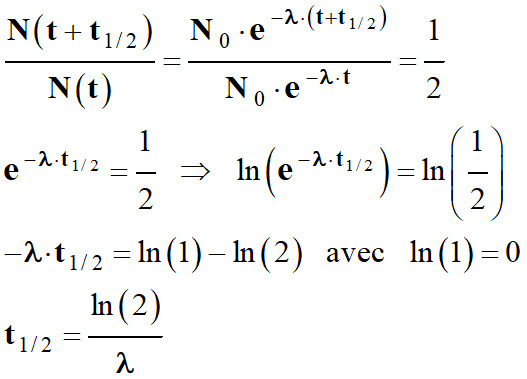
-  La demi-vie n’a qu’une valeur statistique.

-  Elle indique qu’un noyau radioactif a une chance sur deux de disparaître au bout d’une demi-vie.

►  Courbe de décroissance : N = f (t).

-  On peut déterminer la demi-vie d’un noyau radioactif à partir de la courbe de décroissance radioactive.

-  Représentation graphique :

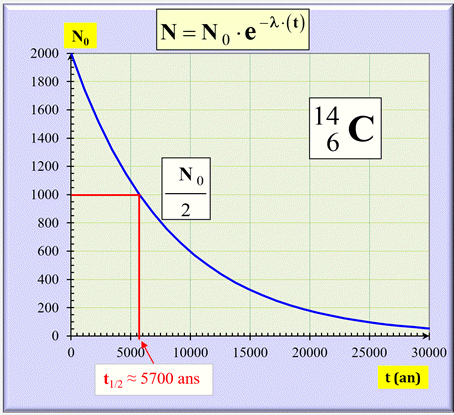
-  La demi-vie du carbone 14 est d’environ 5700 ans.

-  Évolution en fonction de la demi-vie :

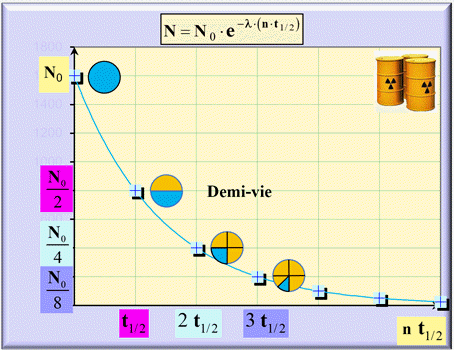
-  On considère que 99 % d’une population de noyaux radioactifs est désintégrée après une durée de sept demi-vies environ.

III- Applications et radioprotection.

1)- Activité d’un échantillon.

-  L’activité A (t) d’un échantillon radioactif à la date t est le nombre de désintégrations par seconde de cet échantillon.

-  L’unité d’activité est le Becquerel Bq en hommage à Henri Becquerel.

-  1 Bq = 1 désintégration par seconde.

-  Si l’on considère qu’entre t et t + Δt, le nombre de noyaux radioactif a diminué de ΔN, l’activité est donnée par la relation :

-   

-  Cette expression représente l’activité moyenne.

-  Pour avoir l’activité à un instant donné, il faut faire tendre Δt →0.

-   

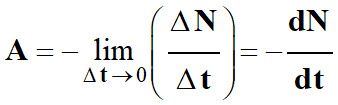
-  En conséquence :

-  L’activité, à un instant donné, est égale à l'opposé de la dérivée par rapport au temps de N (t).

-   

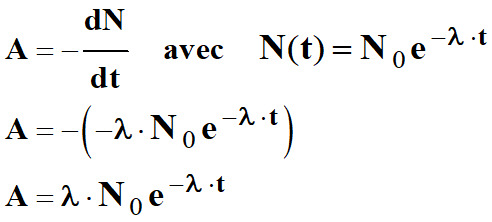
-  Si l’on pose :

-    A₀ = λ . N₀  =>  A (t) = A₀ e ^{– λ . t}

-  La décroissance de l’activité suit la même loi que la décroissance du nombre de noyau radioactif d’un échantillon.

►  Courbe de décroissance : A = f (t) pour le carbone 14

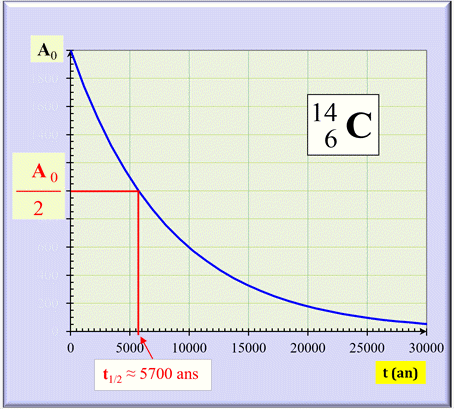
-  Ordre de grandeur des activités : l’eau de mer a une activité de l’ordre de 10 Bq par litre.

-  Le Radon, présent dans l’air, à l’état de trace, a une activité de quelques centaines de Bq.

-  Le corps humain A ≈ 10 ⁴ Bq,

-  Les sources radioactives, utilisées au laboratoire, ont une activité comprise entre 4 × 10⁴ Bq et 4 × 10⁷ Bq.

-  L’activité d’un gramme de radium est supérieure à 10¹⁰ Bq.

-  On utilise aussi le curie comme unité de radioactivité :

-  1 Ci = 3,7 × 10¹⁰  Bq.

-  L’activité du Césium 137 est de l’ordre de 3 × 10⁵  Bq.

2)- Datation d’un objet.

►  La datation au carbone 14.

-  Elle est fondée sur l’utilisation de la loi de décroissance radioactive de l’isotope , radioactif β^–.

-  La demi-vie du carbone 14 est fixée de façon conventionnelle à t _½ = 5734 ± 40 ans (valeur admise en 1961).

-  Le carbone 14 est présent dans l’atmosphère.

-  Il est régénéré par une réaction nucléaire faisant intervenir des neutrons cosmiques et des noyaux d’azote 14 :

-   

-  La proportion de carbone 14 par rapport au carbone 12 est de l’ordre de 10^–12.

-  Il en est de même dans le dioxyde de carbone atmosphérique.

-  On fait l’hypothèse que cette proportion est à peu près constante à l’échelle de quelques dizaines milliers d’années.

-  Tous les organismes vivants échangent du dioxyde de carbone avec l’atmosphère, soit directement, via la photosynthèse, soit indirectement via l’alimentation.

-  Les tissus fixent l’élément carbone.

-  La proportion de carbone 14 par rapport au carbone 12 est la même que la proportion atmosphérique.

-  À leur mort, les organismes cessent de fixer l’élément carbone et le carbone 14 n’est plus régénéré.

-  La quantité de carbone 14 présente dans les tissus diminue alors selon la loi de décroissance radioactive.

-  Pour évaluer l’âge, il faut connaître :

-  L’activité A₀ de 1 g de carbone issu de matière organique vivante et

-  L’activité A de 1 g de carbone issu de l’objet à dater.

-  On calcule le temps t écoulé à partir de la relation suivante :

-  A (t) = A₀ . exp ( – λ . t)

-  A (t) = A₀ e ^{– λ . t}

-   

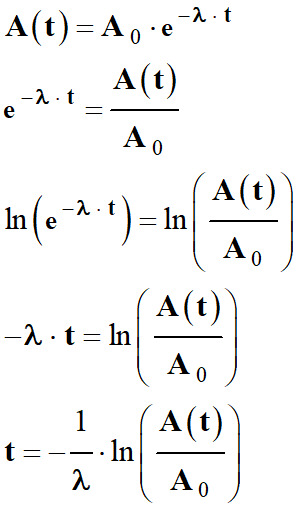
-  On peut calculer le temps écoulé en utilisant la demi-vie du noyau :

-   

-   

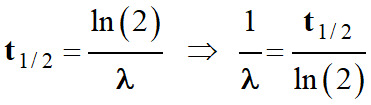
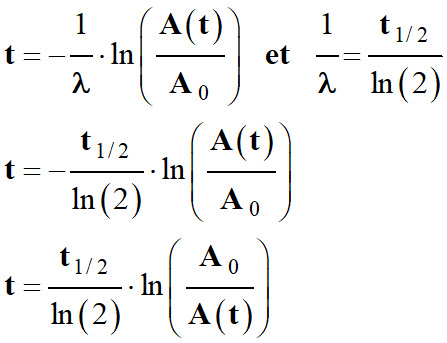
-  La quantité de carbone 14 restant dans un échantillon est encore mesurable jusqu’à 50 000 ans environ.

3)- Médecine et radioprotection.

-  Les expositions aux radiations radioactives sont de deux ordres :

-  Les irradiations directes issues de sources extérieures au corps humain

-  (certaines roches granitiques qui contiennent du thorium 232, le radon 222 présent dans l’atmosphère, …les effets de la centrale de Tchernobyl).

-  Les irradiations internes (iode 131 radioactif qui se fixe dans la glande thyroïde : t_1/2 = 8,02 j )

-  La dose reçue par une personne irradiée détermine :

-  La gravité des effets immédiats (rougeur de la peau, brûlures, ..)

-  La probabilité d’apparition des effets aléatoires (anomalies génétiques ou héréditaires, cancers, leucémies,…)

-  Sources : CEA

-  Les particules α (alpha) sont directement ionisantes mais peu pénétrantes.

-  Ce rayonnement a un pouvoir de pénétration très faible.

-  Il ne parcourt que quelques centimètres dans l’air.

-  Une feuille de papier ou les couches superficielles de la peau l’arrêtent.

-  Les particules β (bêta) sont plus pénétrantes mais moins ionisantes que les particules α.

-  Ce rayonnement ne peut parcourir que quelques mètres dans l’air.

-  Il est stoppé par une vitre ou une feuille d’aluminium.

-  Les rayonnements X et γ ne sont pas directement ionisants, mais ils sont très pénétrants.

-  Ils parcourent dans l’air plusieurs centaines de mètres.

-  Il faut des matériaux denses et épais comme le béton (environ 2 m) et le plomb (plus de 20 cm) pour les arrêter.

-  Ils peuvent traverser jusqu’à 20 cm de plomb.

-  Par interaction avec les atomes des substances traversées, ils peuvent donner naissance à des électrons qui eux sont ionisants

-  La quantité de rayonnements absorbés :

-  Le gray (Gy) est l'unité qui permet de mesurer la quantité de rayonnements absorbés – ou dose absorbée – par un organisme ou un objet exposé aux rayonnements.

-  Le gray a remplacé le rad en 1986 : 1 gray = 100 rads = 1 joule par kilo de matière irradiée.

4)- QCM.

5)- Exercices :