|
|
Sons et effet Doppler |
|
|
|
|
|
Exercices : énoncé et correction
Préparation à ECE : Décalage Doppler 1)- Exercice 03 page 358 : Calculer un niveau
d’intensité sonore. 2)- Exercice 05 page 358 : Utiliser la fonction
logarithme décimal. 3)- Exercice 06 page 358 : Mettre en évidence
une atténuation. 4)- Exercice 08 page 358 : Reconnaître l’effet
Doppler. 5)- Exercice 10 page 359 : Exploiter
qualitativement l’effet Doppler. 6)- Exercice 12 page 359 : Identifier une
expression. 7)- Exercice 14 page 359 : Calculer une valeur
de vitesse. 8)- Exercice 19 page 360 : Au son de la corne de
brume. 9)- Exercice 22 page : Expérience historique
361. 10)- Exercice 23 page 362 : Vitesse d’écoulement
sanguin. 11)- Exercice 24 page 362 : Détermination par effet Doppler de la vitesse d’éloignement d’un émetteur. 12)- DS 01 Effet Doppler et contrôle de
vitesse (50 min) : exercice 28 page 364 13)- DS N° 02 : Niveau sonore et scène de
concert (40 min) : exercice 29 page 364. 14)- Préparation à ECE : Décalage Doppler. |
|
QCM r
|
I-
Le niveau d’intensité sonore.
1)- Le son : une onde mécanique (rappels et compléments)
-
Son émis par un
haut-parleur :
-
Lorsqu’un haut-parleur
est soumis à une tension périodique, sa membrane vibre.
-
Cela crée une
vibration de l’air qui se propage de proche en proche sans transfert de
matière : c’est une onde sonore.
-
Propagation d’un son :
-
Les molécules qui
constituent l’air vibrent et transmettent ce mouvement de proche en proche aux
molécules voisines.
-
Quelques points
importants :
-
Un signal sonore a
besoin d’un milieu matériel pour se propager.
![]() Un signal sonore se
propage dans un milieu matériel solide, liquide ou gazeux mais ne se propage pas
dans le vide.
Un signal sonore se
propage dans un milieu matériel solide, liquide ou gazeux mais ne se propage pas
dans le vide.
-
Les vitesses de
propagation d’un signal sonore dépendent du milieu matériel de propagation.
-
On
parle aussi de la célérité
c d’un son.
-
La valeur approchée de
la vitesse de propagation d’un signal sonore dans l’air à environ 20 ° C est :
-
c
≈
340 m / s.
-
Cette célérité dépend
de la température, du milieu de propagation.
-
La célérité du son est
plus grande dans les solides que dans les liquides et le gaz.
-
Car moins le milieu
est compressible, plus il est difficile à déformer et plus il est rigide.
-
Plus il est rigide,
plus grande est sa célérité.
![]() Un phénomène
périodique est un phénomène qui se reproduit identique à lui-même à intervalles
de temps réguliers.
Un phénomène
périodique est un phénomène qui se reproduit identique à lui-même à intervalles
de temps réguliers.
►
Période et fréquence :
-
La période
T
d’un phénomène périodique est la durée au bout de laquelle le phénomène se
reproduit identique à lui-même.
-
L’unité de période
T
est la seconde, symbole s.
-
La fréquence
f représente
le nombre de période par seconde. On écrit :
-
![]()
-
unité
de fréquence : Hertz : symbole Hz
-
Remarque : Pour
obtenir la fréquence en Hz, il faut pour cela exprimer la période en seconde s.
-
Une onde sonore
périodique possède une :
-
Périodicité temporelle
T et une périodicité spatiale, sa
longueur d’onde
λ.
-
La longueur d’onde est
la distance parcourue par l’onde pendant une période
T.
►
Relation fondamentale.
-
Il découle de ceci que
pendant la durée d’une période T,
l’onde parcourt la distance d
égale à la longueur d’onde λ.
-
Si
v représente la
célérité de l’onde, on peut écrire la relation liant ces différentes grandeurs.
|
|
λ :
Longueur d’onde en mètre (m) |
|
v :
Célérité de l’onde en mètre par seconde (m . s–1) |
|
|
T :
Période en seconde (s) |
|
|
f :
Fréquence en hertz (Hz) |
a)-
Perception des ondes sonores.
-
L’oreille humaine
normale perçoit les ondes sonores dont les fréquences sont comprises entre 20 Hz
et 20 kHz.
-
Les ondes sonores de
fréquences f
< 20 Hz sont appelées infrasons.
-
Les ondes sonores de
fréquences f
> 20 kHz sont appelées ultrasons.
-
Les sons émis par deux
cordes différentes d’une guitare n’ont pas la même fréquence.
-
Ils n’ont pas la même
hauteur.
-
Plus la hauteur d’un
son est grande, plus sa fréquence est élevée et plus le son est aigu.
-
D’autre part, plus un
son est grave et plus sa fréquence est basse.
-
Le timbre d’un son
dépend du nombre et de l’amplitude des harmoniques qui sont présents.
-
Deux sons de même
hauteur émis par des instruments différents ne sont pas perçus de la même
manière, car les harmoniques, associées au fondamental, sont différentes.
-
L’analyse spectrale
d’un son musical permet de caractériser :
-
La hauteur du son qui
est liée à la fréquence f1
du fondamental
-
Le timbre du son qui
est lié au nombre et à l’amplitude des harmoniques présentes.
-
Le timbre du son émis dépend de l'instrument de musique mais aussi du point
d'attaque.
-
La puissance sonore, notée
P, est
l’énergie reçue par l’onde sonore pendant une durée donnée.
- Elle s’exprime en watt (W)
-
C’est la puissance transportée par
l’onde sonore.
-
Le niveau d’intensité
sonore est lié à l’amplitude du signal sonore.
-
C’est la puissance sonore reçue pour
une surface donnée.
-
Plus
l’amplitude du signal sonore est élevée plus l’intensité sonore
I
est grande.
-
L’intensité sonore,
notée I,
caractérise l’intensité du signal reçue par l’oreille.
-
L’intensité sonore I est la puissance
P
par unité de surface
S transportée par une onde sonore.
|
|
I
: Intensité sonore en watt par mètre carré (W . m–2) |
|
P :
Puissance transportée par l’onde sonore en watt (W) |
|
|
S
: Surface de l’onde sonore en mètre carré
(m2) |
-
Elle
s’exprime en watt par mètre carré : W / m2
ou W. m–2
-
L’oreille humaine
normale perçoit les signaux sonores dont l’intensité est comprise entre
-
Une valeur minimale
I0
= 1,0 × 10–12 W. m–2
(seuil d’audibilité)
-
Et une valeur maximale
Imax
= 25 W. m–2 (seuil de
douleur).
-
Ces seuils dépendent
de la fréquence du son perçu et varient en fonction de l’individu.
-
Comme l’écart entre
ces deux valeurs est très grand, on a créé une nouvelle grandeur, qui utilise
une échelle logarithmique : appelée le niveau
d’intensité sonore, notée
L.
3)- Niveau d’intensité sonore.
-
On
définit le niveau d’intensité sonore
L
à partir de l’intensité associée au seuil d’audibilité.
-
Relation
mathématique :
|
|
L :
Niveau d’intensité sonore en décibel (dB) |
|
I :
Intensité du signal en watt par mètre carré (W. m–2) |
|
|
I0
= 1,0
× 10–12 W. m–2 (seuil
d’audibilité) |
-
La notation
log fait référence
à la fonction logarithme décimal.
-
Ainsi, l’échelle de
niveau d’intensité sonore L
varie de 0 dB à environ 140 dB.
-
Alors que l’intensité
sonore I
varie de I0
= 1,0
×
10–12 W. m–2
à 102 W. m–2
►
Quelques propriétés de
la fonction logarithme décimal :
- log 1 = 0 ; log 10 = 1 ;
- log 10n
= n ; log 10–n
= – n
-

![]()

-
Échelles de I
et
L :
-
Remarque : les valeurs de
L (dB) sont plus faciles à manipuler
que les valeurs de
I (W. m–2)
►
Remarque :
-
Que se
passe-t-il lorsque l’intensité sonore
I
est multipliée par deux ?
-
Par définition :
-
Pour
une intensité sonore I, le niveau d’intensité sonore
L est :
-

-
Pour
une intensité sonore I’ = 2
I,
le niveau d’intensité sonore
L’ est :
-

-
Lorsque
l’intensité sonore I est multipliée par deux, le
niveau d’intensité sonore
L augmente de trois décibels (3 dB).
►
Fonction réciproque de
la fonction logarithme décimal :
-
 : cette relation est
équivalente à :
: cette relation est
équivalente à : 
-
Il est
possible de calculer une intensité sonore
I
à partir de la connaissance du niveau d’intensité sonore
L :
-
![]()
-
Relation :
|
|
L :
Niveau d’intensité sonore en décibel (dB) |
|
I :
Intensité du signal en watt par mètre carré (W. m–2) |
|
|
I0
= 1,0
x 10–12 W. m–2 (seuil
d’audibilité) aussi Intensité
sonore de référence |
-
Échelle des niveaux
d’intensité sonore L :
►
L’exposition sonore.
-
Plus le niveau
d’intensité sonore et la durée d’exposition sont élevés et plus les risques
d’atteinte de l’audition sont importants.
-
Lorsque plusieurs
instruments de musique jouent ensemble, les intensités sonores
I dues à chaque
instrument s’ajoutent, alors que les niveaux d’intensité sonore
L ne s’ajoutent
pas.
-
L’exposition sonore tient compte du
niveau d’intensité sonore
et de la durée
d’exposition auxquels l’oreille est soumise.
-
Une
exposition sonore trop élevée peut entraîner des
conséquences irréversibles,
comme une surdité partielle, voire totale.
►
Mise en évidence :
-
On
considère une source ponctuelle qui émet un signal sonore périodique de
puissance P.
-
À la distance
r, l’intensité
sonore est I
et le niveau d’intensité sonore est L.
![]() Quel est le niveau
intensité sonore L’
à la distance r’
= 2 r ?
Quel est le niveau
intensité sonore L’
à la distance r’
= 2 r ?
-
Schéma de la
situation :

-
Au cours de la
propagation de l‘onde sonore, l’énergie de l’onde sonore se répartit sur une
surface de plus en plus grande (surface d’une sphère).
-
Au cours de la
propagation, sans absorption, de l’onde sonore, la puissance
P de la source se
répartit sur la surface S
d’une sphère centrée sur la source.
-
À la distance
r, la surface de
l’onde : S
= 4 π .
r2 ;
-
l’intensité sonore
I : ![]()
-
À la distance
r’ = 2
r, la surface de
l’onde : S’
= 4 π . (r’)2
-
L’intensité sonore
I’ :
-
![]()
-
Or :
-
S’
= 4 π . (r’)2
= 4 π
. (2 r)2
-
S’
= 4 × 4 π
. (r)2
= 4 S
-
Intensité sonore
I’ à la
distance r’
= 2 r :
- 
-
L’intensité sonore a été divisée par 4.
-
Niveau d’intensité
sonore L’ :
-

-
Le niveau d’intensité sonore diminue de 6
dB.
►
Conclusion :
-
L’intensité sonore et
le niveau d’intensité sonore diminuent lorsque l’on s’éloigne de la source
sonore.
-
Lorsque la distance à
la source est multipliée par deux l’intensité sonore est divisée par 4 et le
niveau d’intensité sonore diminue de 6 dB.
►
L’atténuation
géométrique A :
-
C’est la diminution,
du niveau d’intensité sonore, en décibel (dB) lorsque la distance à la source
sonore augmente.
|
A
= Lproche – Léloigné |
A :
Atténuation géométrique en décibel (dB) |
|
Lproche : Niveau d’intensité sonore proche de la source sonore en décibel (dB) |
|
|
Léloigné : Niveau d’intensité sonore éloigné de la source sonore en décibel (dB) |
-
Schéma :

5)- Atténuation par absorption.
-
Lorsqu’une onde sonore
rencontre une paroi, celle-ci peut être :
-
Transmise,
réfléchie
ou absorbée.
-
Schéma :

-
L’atténuation par absorption
A, en décibel, évalue l’efficacité d’un
matériau à lutter contre la transmission de bruit.
|
A
= Lincident – Ltransmis |
A :
Atténuation géométrique en décibel (dB) |
|
Lincident : Niveau d’intensité sonore de l’onde incidente en décibel (dB) |
|
|
Ltransmis : Niveau d’intensité sonore de l’onde transmise en décibel (dB) |
II- L’analyse
spectrale des sons.
-
L’analyse spectrale d’un son musical
permet de caractériser :
-
La hauteur du son qui est liée à la
fréquence f1
du fondamental
-
Le timbre du son qui est lié au nombre
et à l’amplitude des harmoniques présentes.
-
Le timbre du son
émis dépend de l'instrument de musique mais aussi du point d'attaque.
a)-
Exemple : Son produit par une guitare.
-
Le spectre d’un son produit par une
guitare est périodique, mais n’est pas sinusoïdal.
-
La guitare émet un son complexe alors
que le GBF produit un signal pur, un signal sinusoïdal.
-
Enregistrement réalisé avec le logiciel
Gratuit AUDACITY
Son clair : essai02
Son distordu : essai03
-
Un son complexe est formé d’une
superposition de vibrations sinusoïdales ayant des amplitudes et des fréquences
différentes.
-
En 1822, le mathématicien français
Joseph FOURIER a montré que :
-
Tout signal périodique de fréquence
f1
peut être décomposé en une somme de signaux sinusoïdaux de fréquences
fn
multiples de f1.
-
Avec
fn
= n.f1
et n
€
N*
-
La fréquence
f1
est appelée le fondamental.
- C’est la fréquence la plus basse.
-
Elle fixe la hauteur du son ou la note
de musique
-
Les fréquences 2
f1,
3 f1,
…, n.f1
sont appelées harmoniques.
-
L’analyse spectrale d’un son permet
d’en obtenir le spectre en fréquences.
- Le spectre en fréquences d’un son est la représentation graphique de l’amplitude de ses composantes sinusoïdales en fonction de la fréquence.
►
Cas
du son distordu :
-
Le spectre en fréquences du son
distordu émis par une guitare montre plusieurs pics de fréquences :
-
f1
≈ 587 Hz. C’est la fréquence du
fondamental,
le ré3.
-
2 f1,
la première harmonique,
puis, 2 f1
et 6 f1.
-
La hauteur d’un son :
-
Plus la fréquence d’un son est faible
et plus le son est grave ou bas.
-
Plus la fréquence d’un son est élevée
et plus le son est aigu ou haut.
-
Le timbre d’un son :
-
Le timbre d’un son dépend du nombre et
de l’amplitude des harmoniques qui sont présents.
-
Deux sons de même hauteur émis par des
instruments différents ne sont pas perçus de la même manière, car les
harmoniques, associées au fondamental, sont différentes.
-
L’analyse spectrale d’un son musical
permet de caractériser :
-
La hauteur du son est liée à la
fréquence f1du
fondamental.
-
Le timbre du son, est lié au nombre et
à l’amplitude des harmoniques.
►
Exemple
de spectre en fréquences :
-
La fréquence du fondamental du son du
document ci-dessus vaut 440 Hz (La3)
► Signaux délivrés par un GBF relié à un haut-parleur :
-
Le signal triangulaire :
-
Le signal « carré » :
-
Une onde
électromagnétique ou mécanique émise avec une fréquence
fE
est perçue avec une fréquence différente
fR
lorsque l’émetteur et le récepteur sont en déplacement relatif.
-
C’est
ce que l’on appelle l’effet Doppler.
-
L'effet Doppler fut
présenté par Christian Doppler en 1842 pour les ondes sonores puis par
Hippolyte
Fizeau pour les ondes électromagnétiques en 1848.
►
Exemple :
-
le son d’une sirène
est perçu plus aigu lorsque le véhicule qui l’émet se rapproche de
l’observateur.
-
Le son de la sirène
est plus grave lorsque le véhicule qui l’émet s’éloigne de l’observateur.
-
Ce phénomène a été
prévu par C. DOPPLER en 1842 et confirmé expérimentalement en 1845 par C.
BUYS-BALLOT.
-
Il y a aujourd'hui de
multiples applications.
-
Un radar de contrôle
routier est un instrument servant à mesurer la vitesse des véhicules circulant
sur la voie publique à l'aide d'ondes radar.
-
Les fréquences des
ondes radar sont comprises entre 300 MHz et 15 GHz.
-
Le radar émet une onde
continue qui est réfléchie par toute cible se trouvant dans la direction
pointée.
-
Par effet Doppler,
cette onde réfléchie possède une fréquence légèrement différente de celle émise
:
-
plus grande fréquence
pour les véhicules s'approchant du radar et plus petite pour ceux s'en
éloignant.
-
En mesurant la différence de
fréquence entre l’onde émise et celle réfléchie, on peut calculer la vitesse de
la «cible».
-
Mais les radars
Doppler sont utilisés dans d'autres domaines…
-
En
météorologie,
le radar Doppler permet d'analyser la vitesse et le mouvement des perturbations
et de fournir des prévisions de grêle, de pluies abondantes, de neige ou de
tempêtes.
-
En
imagerie médicale,
le radar Doppler permet d'étudier le mouvement des fluides biologiques.
-
Une sonde émet des
ondes ultrasonores et ce sont les globules rouges qui font office d'obstacles et
les réfléchissent.
-
L'analyse de la
variation de la fréquence des ondes réfléchies reçues par cette même sonde
permet ainsi de déterminer la vitesse du sang dans les vaisseaux.
2)- Présentation de l’effet Doppler.
a)-
Détermination par effet
Doppler de la vitesse d’un émetteur sonore qui se rapproche :
![]() La valeur de la
vitesse d’un émetteur E
s’approchant d’un observateur immobile (R)
peut être calculée par effet Doppler.
La valeur de la
vitesse d’un émetteur E
s’approchant d’un observateur immobile (R)
peut être calculée par effet Doppler.
►
On se propose de
retrouver la relation liant les diverses grandeurs mises en jeu :
-
Les différentes
grandeurs physiques :
-
fE
est la fréquence du signal produit par l’émetteur E
;
-
fR
est la fréquence du signal reçu par l’observateur
R ;
-
v
est la valeur de la vitesse de l’onde ;
-
vE
est la valeur de la vitesse de l’émetteur
E
par rapport à l’observateur
R.
-
Référentiel d’étude :
Les valeurs des vitesses sont mesurées dans un référentiel terrestre :
-
Les conditions de
l’étude :
-
On se place dans le
cas où :
-
L’air est supposé
immobile par rapport au son.
-
La vitesse de
déplacement de l’émetteur vE
par rapport au récepteur est faible et inférieure à la vitesse
v de l’onde dans le
milieu de propagation.
-
En conséquence, on
considère que : vE
<< v
-
Schéma représentatif
de la situation :
![]() À la
date t0
= 0 s, E
est à la distance d
de R et émet une onde.
À la
date t0
= 0 s, E
est à la distance d
de R et émet une onde.
![]() Exprimer littéralement la date
t1 au
bout de laquelle le signal est perçu par
R.
Exprimer littéralement la date
t1 au
bout de laquelle le signal est perçu par
R.
-
Expression de la date
t1 :
-
L’onde est émise de
l’émetteur (E)
se déplace à la vitesse v.
-
La distance parcourue
par l’onde est d.
-
Date
t1
au bout de laquelle le signal est perçu par
A :
-

![]() Déterminer l’expression de la distance
dE
parcourue par l’émetteur (E)
pendant la période
TE du signal émis.
Déterminer l’expression de la distance
dE
parcourue par l’émetteur (E)
pendant la période
TE du signal émis.
-
Expression de la
distance dE
parcourue par l’émetteur (E)
pendant la période TE
du signal émis :
-
L’émetteur se déplace
à la vitesse vE
par rapport à l’observateur :
-
dE
= vE
. TE
![]() À la
date TE,
quelle est la distance
d’ entre
E
et R ?
À la
date TE,
quelle est la distance
d’ entre
E
et R ?
-
À la date
TE,
l’émetteur a parcouru la distance dE.
-
L’émetteur se
rapproche de R.
-
d’
= d –
dE
-
d’
= d –
vE
. TE
![]() À la
date TE,
l’émetteur émet de nouveau une onde. À quelle date
t2
l’observateur reçoit-il cette onde ?
À la
date TE,
l’émetteur émet de nouveau une onde. À quelle date
t2
l’observateur reçoit-il cette onde ?
-
Distance à parcourir :
-
d’
= d –
vE
. TE
-
Date
t2
où l’observateur reçoit cette onde :
-
![]()
![]() Quelle
est la durée TR
séparant deux signaux consécutifs captés par l’observateur ? Que représente
TR ?
Quelle
est la durée TR
séparant deux signaux consécutifs captés par l’observateur ? Que représente
TR ?
-
Durée
TR
séparant deux signaux consécutifs captés par l’observateur,
-
TR
= t2
– t1
-

-
La grandeur
TR
représente la période de l’onde perçue par l’observateur.
![]() Exprimer la relation
liant fR
, fE,
v
et vE
dans cette situation.
Exprimer la relation
liant fR
, fE,
v
et vE
dans cette situation.
-
Relation liant
fR,
fE,
v et
vE:
-

![]() Quelle
est l’expression littérale de la valeur de la vitesse
vE
de l’émetteur ?
Quelle
est l’expression littérale de la valeur de la vitesse
vE
de l’émetteur ?
-
Expression littérale
de la valeur de la vitesse vE
de l’émetteur :
-

![]() La valeur de la
vitesse d’un émetteur E
s’éloignant d’un observateur immobile (R)
peut être calculée par effet Doppler.
La valeur de la
vitesse d’un émetteur E
s’éloignant d’un observateur immobile (R)
peut être calculée par effet Doppler.
►
On se propose de
retrouver la relation liant les diverses grandeurs mises en jeu :
-
fE
est la fréquence du signal produit par l’émetteur ;
-
fR
est la fréquence du signal reçu par l’observateur ;
-
v
est la valeur de la vitesse de l’onde ;
-
vE
est la valeur de la vitesse de l’émetteur par rapport à l’observateur.
-
Les valeurs des
vitesses sont mesurées dans un référentiel terrestre :
-
On se place dans le
cas où :
-
L’air est supposé
immobile par rapport au son.
-
La vitesse de
déplacement de l’émetteur par rapport au récepteur est faible et inférieure à la
vitesse de l’onde dans le milieu de propagation.
-
En conséquence, on
considère que : vE
<< v
-
Schéma représentatif
de la situation :
![]() À la
date t0
= 0 s, E
est à la distance d
de R et émet une onde. Exprimer
littéralement la date
t1 au
bout de laquelle le signal est perçu par
R.
À la
date t0
= 0 s, E
est à la distance d
de R et émet une onde. Exprimer
littéralement la date
t1 au
bout de laquelle le signal est perçu par
R.
-
Expression de la date
t1 :
-
L’onde est émise de
l’émetteur (E)
se déplace à la vitesse v.
-
La distance parcourue
par l’onde est d.
-
Date
t1
au bout de laquelle le signal est perçu par
R :
- 
![]() Déterminer l’expression de la distance
dE
parcourue par l’émetteur (E)
pendant la période
TE du signal émis.
Déterminer l’expression de la distance
dE
parcourue par l’émetteur (E)
pendant la période
TE du signal émis.
-
Expression de la
distance dE
parcourue par l’émetteur (E)
pendant la période TE
du signal émis :
-
L’émetteur se déplace
à la vitesse vE
par rapport à l’observateur :
-
dE
= vE
. TE
![]() À la
date TE,
quelle est la distance
d’ entre
E
et R ?
À la
date TE,
quelle est la distance
d’ entre
E
et R ?
-
À la date
TE,
l’émetteur a parcouru la distance dE.
-
L’émetteur s’éloigne de R.
-
d’
= d +
dE
-
d’
= d +
vE
. TE
![]() À la
date TE,
l’émetteur émet de nouveau une onde. À quelle date
t2
l’observateur reçoit-il cette onde ?
À la
date TE,
l’émetteur émet de nouveau une onde. À quelle date
t2
l’observateur reçoit-il cette onde ?
-
Distance à parcourir :
-
d’
= d +
vE
. TE
-
Date
t2
où l’observateur reçoit cette onde :
-
![]()
![]() Quelle
est la durée TR
séparant deux signaux consécutifs captés par l’observateur ? Que représente
TR ?
Quelle
est la durée TR
séparant deux signaux consécutifs captés par l’observateur ? Que représente
TR ?
-
Durée
TR
séparant deux signaux consécutifs captés par l’observateur.
-
TR
= t2
– t1
-

-
La grandeur
TR
représente la période de l’onde captée (reçue) l’observateur.
![]() Exprimer la relation liant
fR,
fE,
v et
vE
dans cette situation.
Exprimer la relation liant
fR,
fE,
v et
vE
dans cette situation.
-
Relation liant
fR,
fE,
v et
vE:
-

![]() Quelle
est l’expression littérale de la valeur de la vitesse
vE
de l’émetteur ?
Quelle
est l’expression littérale de la valeur de la vitesse
vE
de l’émetteur ?
-
Expression littérale
de la valeur de la vitesse vE
de l’émetteur :
-

c)-
Une autre approche de l’effet
Doppler (avec la longueur d’onde λ) :
►
Émetteur sonore qui
se rapproche du récepteur :
-
La valeur de la vitesse d’un émetteur E s’approchant d’un observateur immobile (R) peut être calculée par effet Doppler
-
fE
est la fréquence du signal produit par l’émetteur ;
-
λE
est la longueur d’onde du son émis par l’émetteur
-
fR
est la fréquence du signal reçu (perçu) par l’observateur ;
-
λR
est la longueur d’onde du son reçu (perçu) par l’observateur ;
-
v
est la valeur de la vitesse de l’onde ;
-
vE
est la valeur de la vitesse de l’émetteur par rapport à l’observateur.
-
Les valeurs des
vitesses sont mesurées dans un référentiel terrestre :
-
On se place dans le
cas où :
-
L’air est supposé
immobile par rapport au son.
-
La vitesse de
déplacement de l’émetteur par rapport au récepteur est faible et inférieure à la
vitesse de l’onde dans le milieu de propagation.
-
En conséquence, on
considère que : vE
<< v
-
Schéma représentatif
de la situation :
-
Au temps
t = 0 s, l’émetteur
émet le bip 1 de fréquence fE
-
Au temps
t =
TE,
l’émetteur émet le bip 2 de fréquence fE.
-
Pendant la durée
TE,
l’émetteur s’est rapproché de la distance
d :
-
d
= vE.TE
-
Les deux bips sont
séparés de la distance d’ :
-
d’
= v.TE
– vE.TE
-
La distance
d’ représente la
longueur d’onde du signal perçu par l’observateur
-
λR
= v.TE
– vE.TE
-
D’autre part :
-
λE
= v.TE
-
On tire :
-
λR
= λE
– vE.TE
-
L’onde perçue par le
récepteur a une longueur d’onde inférieure (une période inférieure ou une
fréquence plus grande) que celle envoyée par l’émetteur.
-
Expression de la
vitesse vE dans
ce cas :
-

►
Émetteur sonore qui
s’éloigne du récepteur :
-
La valeur de la
vitesse d’un émetteur E
s’éloignant d’un observateur immobile (R)
peut être calculée par effet Doppler.
-
fE
est la fréquence du signal produit par l’émetteur ;
-
fR
est la fréquence du signal reçu par l’observateur ;
-
v
est la valeur de la vitesse de l’onde ;
-
vE
est la valeur de la vitesse de l’émetteur par rapport à l’observateur.
-
Les valeurs des
vitesses sont mesurées dans un référentiel terrestre :
-
On se place dans le
cas où :
-
L’air est supposé
immobile par rapport au son.
-
La vitesse de
déplacement de l’émetteur par rapport au récepteur est faible et inférieure à la
vitesse de l’onde dans le milieu de propagation.
-
En conséquence, on
considère que : vE
<< v
-
Schéma représentatif
de la situation :
-
Au temps
t = 0 s, l’émetteur
émet le bip 1de fréquence fE
-
Au temps
t =
TE,
l’émetteur émet le bip 2 de fréquence fE.
-
Pendant la durée
TE,
l’émetteur s’est éloigné de la distance
d :
-
d
= vE.TE
-
Les deux bips sont
séparés de la distance d’ :
-
d’
= v.TE
+ vE.TE
-
La distance
d’ représente la
longueur d’onde du signal perçu par l’observateur
-
λB
= v.TE
+ vE.TE
-
D’autre part :
-
λE
= v.TE
-
On tire :
-
λR
= λE
+ vE.TE
-
L’onde perçue par le
récepteur a une longueur d’onde plus grande (une période supérieure ou une
fréquence plus petite) que celle envoyée par l’émetteur.
-
Expression de la
vitesse vE dans
ce cas :
-

-
Lorsque l’émetteur
E se
rapproche du récepteur R :
|
Longueur d’onde |
Période |
Fréquence |
|
|
|
|
-
Expression de la
vitesse : 
-
Lorsque l’émetteur
E s’éloigne
du récepteur R :
|
Longueur d’onde |
Période |
Fréquence |
|
|
|
|
-
Expression de la
vitesse : 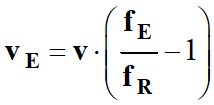
|
- L’effet Doppler est l’existence d’un décalage entre : la fréquence fE d’une onde électromagnétique ou mécanique émise et la fréquence fR de l’onde reçue
lorsque la distance
d
entre l’émetteur E et le récepteur R varie.
-
Le décalage Doppler
est noté :
-
Δf
= fR
– fE |
-
Comme
les grandeurs λ,
T
et f
sont liées entre elles, l’effet Doppler correspond aussi à un décalage de
période et de longueur d’onde.
-
Le
signe du décalage Doppler dépend du sens d’évolution de la distance entre
l’émetteur E et le récepteur
R.
►
Lorsque
l’émetteur E se rapproche du récepteur
R :
-
La
distance entre l’émetteur
E et le récepteur
R diminue :
|
Longueur d’onde |
Période |
Fréquence |
|
|
|
|
-
La
longueur d’onde λR
< λE,
la période TR
< TE
et la fréquence fR
> fE.
-
Le son perçu est plus
aigu.
-
Expression de la
vitesse : 
-
Expression du décalage
Doppler :
-
Δf
= fR
– fE
-

-
Comme vE
<< v, dans ce cas, le décalage
Doppler est positif :
Δf > 0
►
Lorsque
l’émetteur E s’éloigne du récepteur
R :
-
La
distance entre l’émetteur
E et le récepteur
R augmente :
|
Longueur d’onde |
Période |
Fréquence |
|
|
|
 |
-
La
longueur d’onde λR
> λE,
la période TR
> TE
et la fréquence fR
< fE
-
Le son perçu est plus
grave.
-
Expression de la
vitesse : 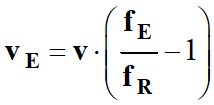
-
Expression du décalage
Doppler dans ce cas :
-
Δf
= fR
– fE
- 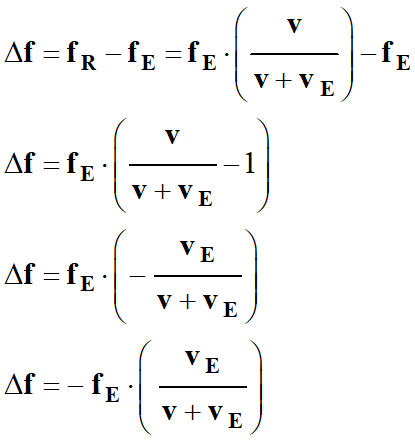
-
Dans ces cas, le décalage Doppler est négatif : Δf < 0
►
Remarque :
-
Si
l’émetteur E est immobile par rapport au
récepteur R, alors :
-
λR
= λE,
TR
= TE
et fR
= fE.
-
D’autre part, l’effet
Doppler constitue une méthode de mesure de la valeur de la vitesse.
-
Le spectre de la
lumière émise par une étoile comporte des raies d’absorption caractéristiques
des éléments présents dans l’atmosphère qui l’entoure.
-
En appliquant les conséquences de
l’effet C. Doppler à la lumière, H.
Fizeau (1819-1896) a postulé en 1848 que :
-
Si une étoile
s’éloigne ou s’approche de la Terre, on doit observer un décalage de ses raies
d’absorption.
-
La mesure de ce
décalage permettrait de calculer la vitesse radiale de l’étoile.
-
Les télescopes
modernes et les outils informatiques permettent aujourd’hui de calculer les
vitesses radiales des étoiles en analysant de très nombreuses raies.
-
L’effet Doppler-Fizeau
permet de calculer la valeur de la vitesse radiale d’une étoile en comparant les
longueurs d’onde de son spectre d’absorption à celles d’un spectre de référence.
-
Lorsque l’étoile
s’éloigne de la Terre, on observe un décalage vers les grandes longueurs d’onde
c’est-à-dire vers le rouge pour les raies du visible (Redshift).
-
Lorsque l’étoile se
rapproche de la Terre, on observe un décalage vers les petites longueurs d’onde
c’est-à-dire vers le bleu pour les raies du visible (Blueshift).
-
Remarque : la vitesse
radiale d’une étoile est la vitesse à laquelle elle s’éloigne ou s’approche de
la Terre.
-
Le décalage de la
longueur d’onde dû à l’effet Doppler-Fizeau permet de calculer la valeur de la
vitesse d’éloignement ou de rapprochement d’une galaxie par rapport à la Terre.
|
Décalage vers le rouge (Redshift) des raies entre le spectre obtenu pour une source et un observateur immobile (spectre a ) et celui
obtenu pour un éloignement entre la
source et l’observateur
(spectre
b). |
|
QCM r
|
|
Exercices : énoncé et correction
Préparation à ECE : Décalage Doppler 1)- Exercice 03 page 358 : Calculer un niveau
d’intensité sonore. 2)- Exercice 05 page 358 : Utiliser la fonction
logarithme décimal. 3)- Exercice 06 page 358 : Mettre en évidence
une atténuation. 4)- Exercice 08 page 358 : Reconnaître l’effet
Doppler. 5)- Exercice 10 page 359 : Exploiter
qualitativement l’effet Doppler. 6)- Exercice 12 page 359 : Identifier une
expression. 7)- Exercice 14 page 359 : Calculer une valeur
de vitesse. 8)- Exercice 19 page 360 : Au son de la corne de
brume. 9)- Exercice 22 page : Expérience historique
361. 10)- Exercice 23 page 362 : Vitesse d’écoulement
sanguin. 11)- Exercice 24 page 362 : Détermination par effet Doppler de la vitesse d’éloignement d’un émetteur. 12)- DS 01 Effet Doppler et contrôle de
vitesse (50 min) : exercice 28 page 364 13)- DS N° 02 : Niveau sonore et scène de
concert (40 min) : exercice 29 page 364. 14)- Préparation à ECE : Décalage Doppler. |
|
|