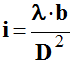|
Chap. N° 03 |
Propriétés des ondes. Exercices. |
|
|
|
I-
Exercice 6 page 76 : Connaître le phénomène de
diffraction.
|
On intercale un trou circulaire de petite dimension devant un faisceau laser. Décrire la figure obtenue sur un écran placé à
quelques mètres de l’ouverture. |
|
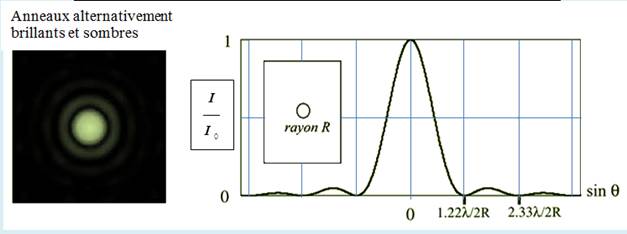
Dans le cas d’une ouverture circulaire, la figure de diffraction obtenue a la symétrie de révolution : Elle se compose d’anneaux alternativement sombres et brillants, entourant
une tache centrale beaucoup
plus brillante, qui porte le nom de
tache d’Airy. Les limites angulaires de la
tache d’Airy sont données par :
-
λ0 : longueur d’onde
dans le vide de la radiation lumineuse -
d : diamètre du trou. La luminosité
des anneaux brillants diminue au fur et à mesure que
l’on s’éloigne de la tache centrale. Ce phénomène se produit lorsque
l’ouverture par laquelle la lumière passe est de
petite taille et du même ordre de grandeur que la
longueur d’onde de la radiation. L’ouverture a diffracté la
lumière du laser. Exemple avec un laser vert :
|
II-
Exercice 9 page 76 : Connaître le phénomène
d’interférences.
|
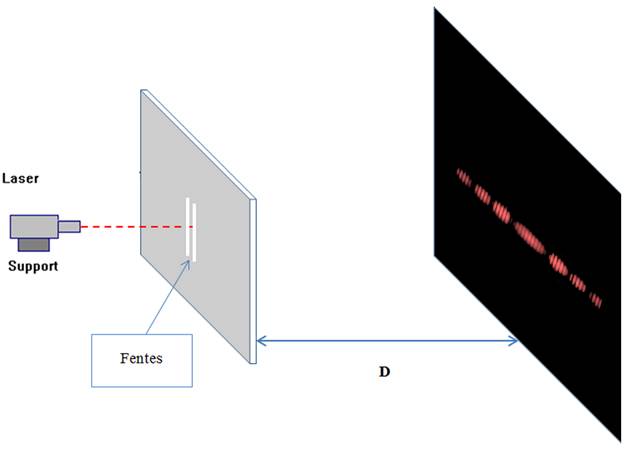
Un système de deux fentes
d’Young est éclairé à l’aide d’une source
monochromatique. Décrire la figure obtenue sur
un écran placé à quelques mètres de la fente. |
|
Figure de diffraction obtenue
avec une fente fine :
Figure obtenue avec deux fentes
fines (Fentes d’Young) :
Au phénomène de diffraction se
superpose le phénomène d’interférences. Sur la tache centrale de diffraction, on observe des franges d’interférences. Ces franges sont alternativement sombres et brillantes. Elles sont parallèles entre elles et
parallèles aux deux fentes d’Young.
|
III- Exercice 13 Page 76 : Comparer des fréquences.
|
Une étoile émet
une onde électromagnétique de fréquence
fE
et de célérité
c. Elle s’éloigne d’un observateur B avec une vitesse VE. La fréquence
fB de l’onde perçue vérifie la
relation :
- 1)- Vérifier l’homogénéité de cette expression par une analyse dimensionnelle. 2)-
Comparer les fréquences fE et
fB. |
|
1)-
Analyse dimensionnelle de l’expression :

-
L’expression est bien
homogène à l’inverse d’une durée, c’est bien une
fréquence. 2)-
Comparaison des fréquences fE et
fB.
-
De l’expression
-
Car :
|
IV-
Exercice 15 page 77 : Largeur d’une tache centrale.
|
On réalise une
figure de diffraction en éclairant une fente de
largeur a
à l’aide d’un faisceau laser de longueur d’onde
λ dans
le vide. Cette figure est obtenue sur un
écran situé à une distance
D de la
fente. 1)-
Recopier et compléter le schéma ci-dessus en faisant
apparaître le demi-angle de diffraction
θ, la distance D et la largeur
ℓ de la tache centrale. 2)-
Quelle relation existe-t-il entre
θ,
λ et a ? 3)-
Autre relation : a)- L’angle θ étant petit et exprimé en radian, on a la relation θ ≈ tan θ. Établir la relation entre la largeur
de la tache centrale ℓ, l’angle θ et
la distance D. b)-
En déduire une relation
entre ℓ, λ, D et a. 4)-
Comment évolue la largeur de la tache centrale si : a)-
La largeur de la fente
double ? Est divisée par deux ? b)-
La distance entre la fente
et l’écran double ?
- Justifier les
réponses. |
|
1)-
Schéma complété : 2)- Relation entre θ, λ et a.
- On peut rappeler les
unités : θ (rad),
λ
(m)et a (m).
- D’autre part, lorsque
la largeur de la fente diminue, la largeur de la
tache centrale augmente.
-
3)-
Autre relation : a)-
Relation entre la largeur de
la tache centrale ℓ, l’angle θ et la
distance D :
-
b)-
Relation entre ℓ,
λ, D et a :
-
En combinant (1) et
(2), on tire :
-
4)-
Évolution de la largeur de la tache centrale : a)-
La largeur de la fente
double
- En conséquence
-
- Si la largeur de la
fente double, la largeur de la tache centrale est
divisée par deux.
- La largeur de la
fente est divisée par deux :
-
- Si la largeur de la
fente est divisée par deux, la largeur de la tache
centrale est multipliée par deux. b)-
La distance entre la fente
et l’écran double :
-
- Si la distance entre
la fente et l’écran double, la largeur de la tache
centrale est multipliée par deux
|
V-
Exercice 17 page 77 : Mailles du voilage.
|
Rémi souhaite déterminer la dimension d’un voilage. Pour
cela, il réalise le montage suivant : Figure obtenue :
Le laser émet une lumière de longueur d’onde dans le vide λ = 633 nm. Il est placé à une distance d = 20,0 cm du voilage.
La
distance entre le voilage et l’écran vaut D =
(2,00 ± 0,01) m.
Rémi
observe que la tache centrale obtenue sur l’écran
est composée de points lumineux équidistants séparés
par des zones sombres. La
distance séparant deux points consécutifs est :
i = (0,45 ± 0,01) cm 1)- Le voilage se comporte comme un réseau à deux dimensions comportant un grand nombre de trous. Quel est le phénomène responsable de l’observation de points lumineux équidistants sur l’écran ? 2)- Comment appelle-t-on la distance i
séparant deux points lumineux consécutifs sur
l’écran ? 3)- En notant a la distance séparant deux
trous consécutifs du voilage, on a : -
- Calculer la valeur de a et son
incertitude. - Pour le calcul de l’incertitude on
prendra : - On suppose la longueur d’onde du laser
connue avec exactitude. - Le résultat sera donné sous la forme
a ± U (a).
|
|
1)- Phénomène observé : - Au phénomène de diffraction se
superpose le phénomène d’interférences. - Phénomène de diffraction provoqué par
le fait que les trous sont de petites dimensions. - Phénomène d’interférences car les
trous forment autant de sources lumineuses cohérentes, synchrones qui interfèrent. 2)- Nom de la distance i séparant deux
points lumineux consécutifs sur l’écran : -
Lors d’interférences lumineuses,
l’interfrange, notée i, est la distance
séparant deux franges brillantes consécutives ou
deux franges sombres consécutives. 3)- Valeur de a et son incertitude : -
- Incertitude sur la valeur de a : -
- En conséquence : a = (281 ±
6,4) μm
|
VI-
Exercice 21 page 79 : Contrôle de vitesse.
|
Le cinémomètre
MESTA 208® est utilisé afin de contrôler par effet
Doppler la valeur de la vitesse instantanée des
véhicules automobiles. Un élève cherche à modéliser le principe de la mesure. Il dispose d’un émetteur et
d’un récepteur d’ondes ultrasonores, ainsi que d’un
véhicule jouet pouvant se déplacer à vitesse
constante. La situation est représentée
sur le document ci-dessous. Le cinémomètre MESTA 208® mesure la vitesse instantanée des véhicules automobiles. Il
fonctionne par application de l’effet Doppler dans
le domaine des ondes électromagnétiques
(micro-ondes). 1)- Approche expérimentale : a)-
Quelle est la différence entre le principe de
fonctionnement du cinémomètre et l’expérience
historique de Buys-Ballot réalisée en 1845 (voir
exercice 26 page 81) ? b)-
Quelle propriété des ondes vue en Seconde
cette expérience utilise-t-elle ? c)-
Déterminer, à partir du schéma, si la mesure
de la vitesse de la vitesse est faite lorsque le
véhicule s’approche ou s’éloigne du cinémomètre ? d)- On note fE la fréquence de l’onde émise et fR celle de l’onde reçue par le récepteur. Lors d’un tel mouvement,
fE est-elle supérieure ou inférieure
à fR ? 2)- On réalise l’acquisition informatisée des
signaux émis et reçus. Le logiciel permet de repérer
les fréquences de chacun des signaux. -
Déterminer fE et
fR. 3)- La célérité des ondes ultrasonores VS est égale à 340 m / s. On propose trois relations permettant de calculer la valeur de la vitesse V
du véhicule, mesurée par rapport au sol et telle que
V << VS. a)-
Déterminer la relation correcte à partir
d’une analyse dimensionnelle et de la situation
illustrée par le document.
b)-
D’où vient le nombre 2 dans l’expression de
la vitesse ? On pourra s’aider d’un schéma. c)-
Calculer la valeur de la vitesse V du
véhicule. 4)- Le déplacement du véhicule a été filmé, pour
obtenir puis représenter sa position x en
fonction du temps. a)-
Déterminer graphiquement la vitesse Vvidéo,
du véhicule, obtenue à partir de la vidéo du
mouvement. b)-
Conclure en comparant les valeurs de V
et Vvidéo. |
|
1)- Approche expérimentale : a)-
Différences entre les expériences : -
Dans le cas du cinémomètre, un
émetteur fixe émet un signal et ce signal se
réfléchit sur un véhicule qui se rapproche à la
vitesse V du récepteur qui est fixe. -
Dans le cas de l’expérience de
Buys-Ballot, l’émetteur est situé sur le véhicule
qui se rapproche du récepteur à la vitesse V. b)-
La propriété des ondes mise en évidence : on
met ici en évidence la réflexion des ondes. c)-
La mesure de la vitesse est faite lorsque le
véhicule se rapproche du cinémomètre. d)-
fE est-elle supérieure ou
inférieure à fR : -
L’émetteur émet un signal de fréquence
fE qui se déplace à la célérité
c vers le
véhicule qui se rapproche à la vitesse
V. -
En conséquence, la fréquence du signal
reçu fR est supérieure à celle du
signal émis fE. ►
Une méthode de résolution : -
On note : -
fE : fréquence du
signal produit par l’émetteur ; -
fR : fréquence du
signal reçu par le récepteur ; -
c : célérité de l’onde ; -
VE : vitesse du
véhicule dans le référentiel lié au cinémomètre. -
Émission du premier Bip : -
Distance parcourue par le véhicule
lorsque l’onde l’atteint :
d -
Distance parcourue par l’onde : -
Aller :
d -
Retour :
d -
Pour parcourir la distance aller d,
l’onde a mis la durée t1–
t0. -
-
Durée pour parcourir le retour :
-
-
Date d’arrivée :
-
-
Émission du second bip : -
Le second Bip est émis au temps TE. -
Distance parcourue par la voiture
pendant la durée TE : -
d’ = VE .
TE -
Temps mis par l’onde pour arriver sur
le véhicule : -
-
Date à laquelle se produit la
réflexion : -
-
Durée du parcours retour : -
-
Date à laquelle le second bip arrive
au niveau du récepteur : -
-
Que représente la durée t’2
– t2 ? -
Cette durée représente la période TR
du signal reçu par le cinémomètre. -
-
Expression de la fréquence fR
: -
-
De la relation (1), on peut déduire
que TR < TE car -
En conséquence : fR
> fE. 2)- Détermination de fE et
fR : -
Comme fR
> fE : -
fE
= 40,000 kHz
et
fR
= 40,280 kHz
3)- Étude avec les ondes ultrasonores : a)-
Relation correcte :
b)-
Le nombre 2 dans l’expression de la vitesse : -
- L’apparition du nombre 2 dans cette expression provient du fait que l’onde analysée est
obtenue par réflexion. L’onde fait un aller-retour
pour arriver au récepteur. c)-
Valeur de la vitesse V du véhicule : -
L’expression (2) appliquée aux ondes
ultrasonores donne : -
-
De l’expression (2’), on tire : -
-
Application numérique : -
4)- Étude graphique de la vitesse : a)-
Détermination graphique de la vitesse : -
Le graphique représente des variations
de la position x en fonction du temps. -
Les points sont sensiblement alignés
et la droite moyenne est du type x = a
. t + x0 -
Le coefficient directeur a de
la droite moyenne tracée représente la vitesse VVidéo
du véhicule. -
Valeur de la vitesse : -
b)-
Comparaison et conclusion : -
VE ≈ 1,18 m / s et
VVidéo ≈ 1,07 m / s -
On peut calculer l’erreur relative
entre ces deux valeurs : -
-
Le résultat est médiocre. Cela est
certainement lié à l’exploitation du graphique qui
n'est pas très précise.
|
VII- Exercice 23 page 80 : Différence de marche.
|
On réalise le
montage suivant dans lequel S est une source de
lumière monochromatique de longueur d’onde dans le
vide λ = 488 nm.
Cette source éclaire deux
fentes étroites S1 et S2,
séparées par une distance b = 0,20 mm. On a SS1 =
SS2. Schéma :
On observe la
figure obtenue sur un écran situé à la distance D
= 1,00 m du plan de ces fentes. On considère sur l’écran l’axe (Ox), O se trouve sur la médiatrice de [S1S2]. Pour un
point P de cet axe d’abscisse xP,
la différence de marche entre les deux ondes
provenant de S1 et S s’écrit :
1)- Étude au point O : a)-
Quelle est la différence de marche en O ? b)-
Qu’observe-t-on sur l’écran en ce point ? 2)- Étude au point P : a)-
Calculer la différence de marche au point
P d’abscisse xP = 6,1 mm. b)-
Qu’observe-t-on sur l’écran en ce point ?
|
|
1)- Étude au point O : a)-
Différence de marche en O : -
Pour des raisons de symétrie, la
différence de marche au point O est nulle. b)-
On observe une frange brillante sur l’écran. 2)- Étude au point P : a)-
Différence de marche au point P
d’abscisse xP = 6,1 mm -
b)-
Observation sur l’écran : -
Si δ
= k . λ, -
Les deux ondes arrivent au point P
en phase et elles ajoutent leurs effets. -
On dit que l’interférence est
constructive. -
On obtient une frange brillante. -
Si, -
Les deux ondes arrivent au point M
en opposition de phase et elles annulent leurs
effets. -
On dit que l’interférence est
destructive. -
On obtient une frange sombre. -
Dans le cas présent : -
-
Comme
►
Pour retrouver l’expression de la
différence de marche au point P : -
Si les deux rayons lumineux se
déplacent dans le même milieu d’indice n, il
existe une différence de chemin optique entre les
deux rayons. -
On parle de différence de marche
δ. -
Il existe entre les deux ondes
lumineuses arrivant en P une différence de
marche δ. -
δ = |(SS2 +
S2P) – (SS1
+ S1P)| -
Comme SS2 =
SS1 -
δ = |S2P
– S1P)| -
On va utiliser : -
Le fait que D >> b et
D >> x -
L’approximation suivante : (1 + ε)n
≈ 1 + n ε avec ε << 1. -
La relation : A2 –
B2 = (A + B) (A
–B) -
Le théorème de Pythagore. -
Expression de S2P
: -
-
-
Expression de S1P
: de la même façon -
-
Étude de l’expression : -
La grandeur x << D et la
grandeur b <<
D -
En conséquence : -
On peut utiliser l’approximation
suivante : (1 + ε)n ≈ 1 + n ε
avec ε << 1. -
-
De la même façon : -
-
Expression de la différence de
marche : -
δ = |S2P
– S1P)| = S2P
– S1P dans le cas de
la figure étudiée. -
-
On va utiliser le fait que :
A2 –
B2
= (A +
B) (A
–B) -
-
Il y a interférences constructives si
δ = k . λ (un nombre entier de
longueurs d’onde) -
Il y a interférences destructives si |
VIII- Exercice 24 Page 80 : Calcul d’une longueur d’onde.
|
Deux fentes étroites et parallèles, séparées par une distance b = 0,20 mm, sont éclairées par un faisceau de lumière monochromatique de longueur d’onde λ dans le vide. On observe
sur l’écran, placé à une distance D
= 1,00 m du plan de ces fentes, une alternance de
franges brillantes et sombres. La distance séparant les
milieux de deux franges brillantes (ou sombres)
consécutives
est appelée « interfrange » et notée
i. 1)- Afin de déterminer l’interfrange, on mesure la distance d comme indiqué sur le schéma ci-dessous. - On obtient d = 30 mm. Calculer
l’interfrange i. -
Schéma : 2)- Étude de la relation : a)- Par analyse dimensionnelle, déterminer l’expression qui permet de calculer l’interfrange
i parmi les propositions suivantes :
b)-
En déduire la longueur d’onde λ
de la lumière. 3)- Pourquoi a-t-on mesuré plusieurs
interfranges ?
|
|
1)- Valeur de l’interfrange i : -
d = 10 i
=> i = 3,0 mm 2)- Étude de la relation : a)-
Analyse dimensionnelle :
-
La bonne relation est la relation
(B) : b)-
Longueur d’onde λ de la lumière : -
3)- On mesure plusieurs interfranges pour avoir
une plus grande précision sur la mesure. - Comme l’interfrange i est très petit, le fait de mesurer d = 10 i, - On
réduit ainsi l’erreur systématique sur la mesure.
- L’erreur commise est la même si on mesure i ou 10 i - (on utilise le même
instrument de mesure).
|
|
|






















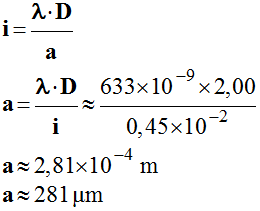














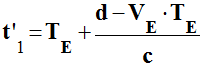





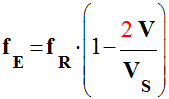





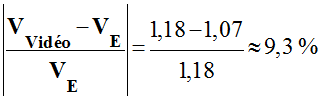




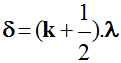







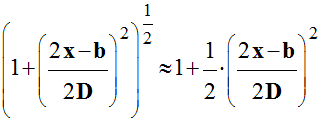



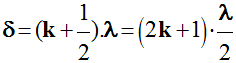 (un nombre impair de demi-longueurs d’onde
λ)
(un nombre impair de demi-longueurs d’onde
λ)