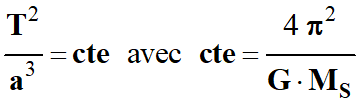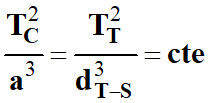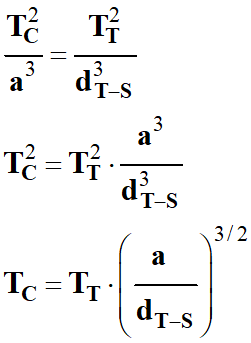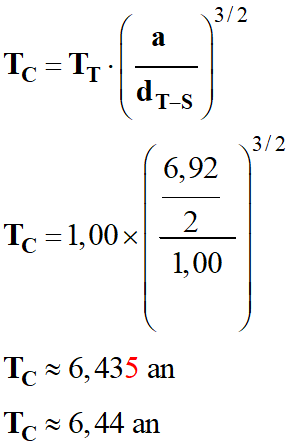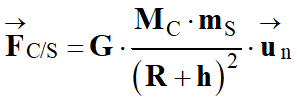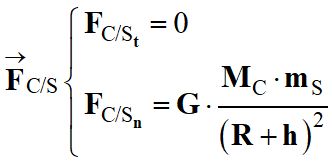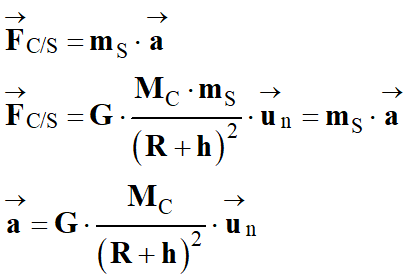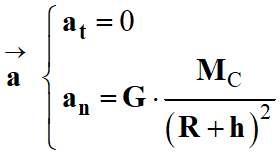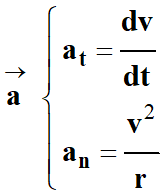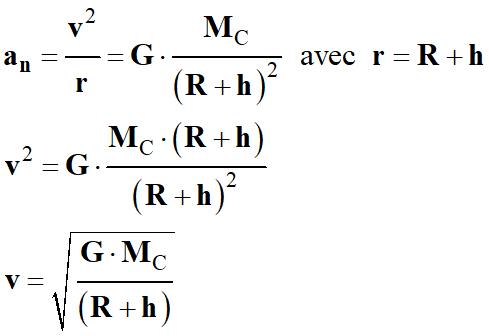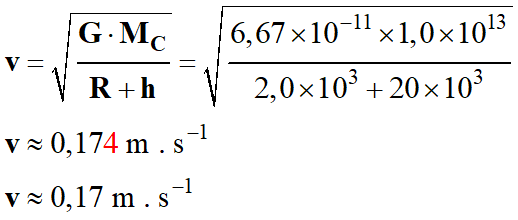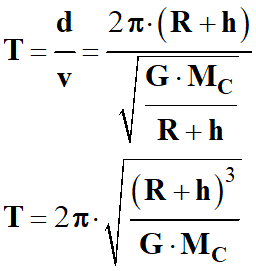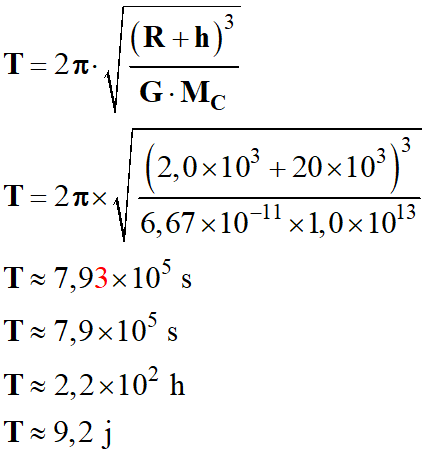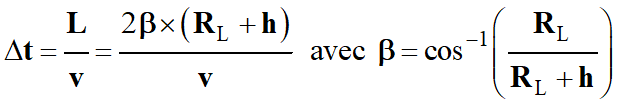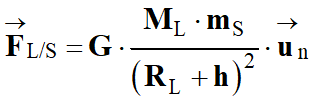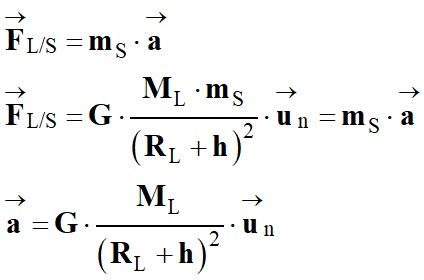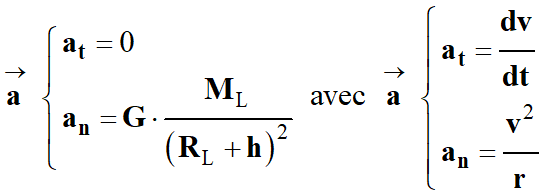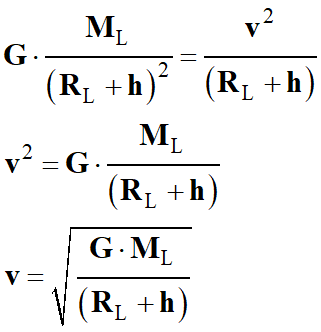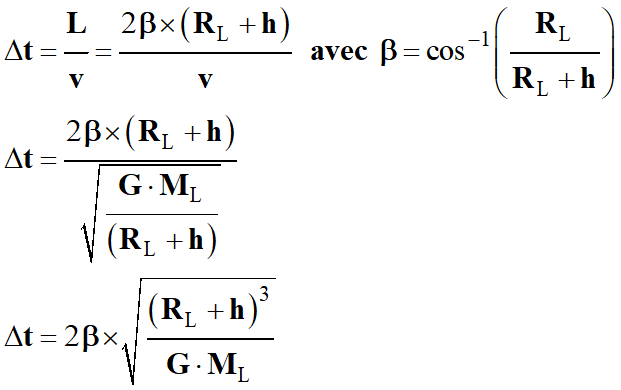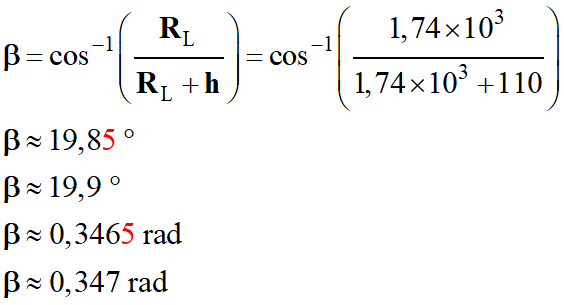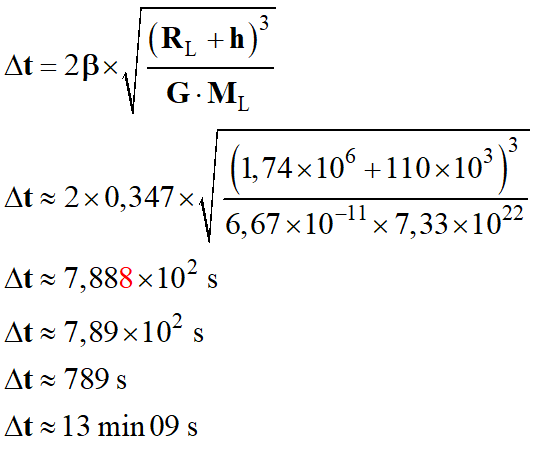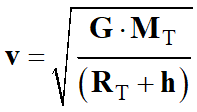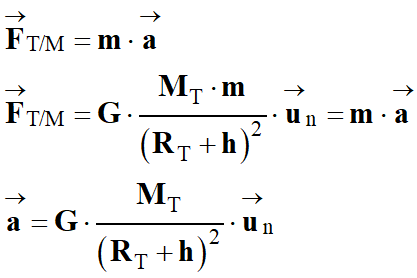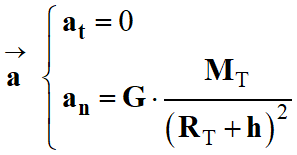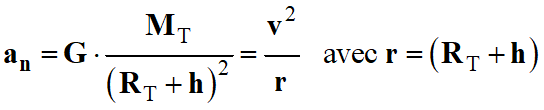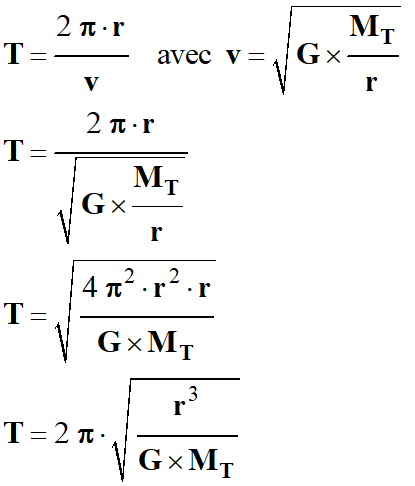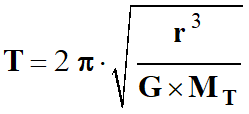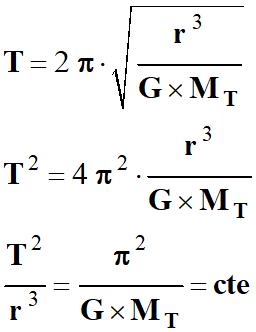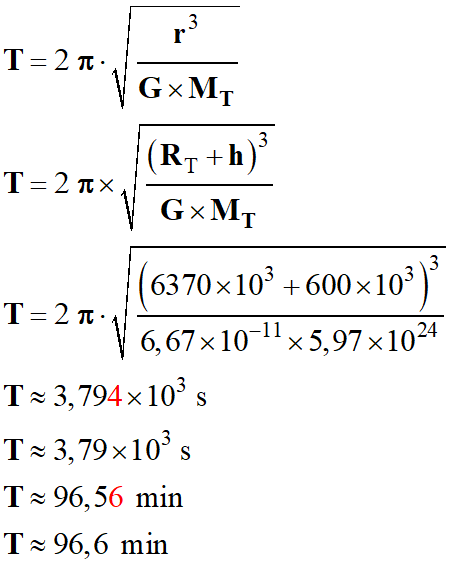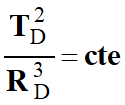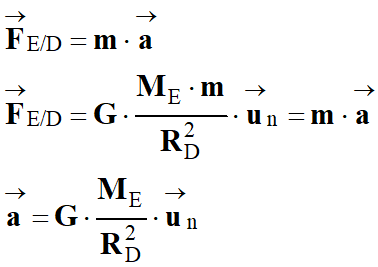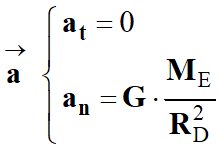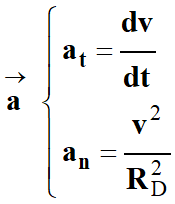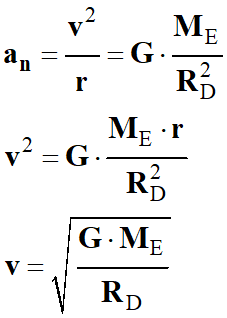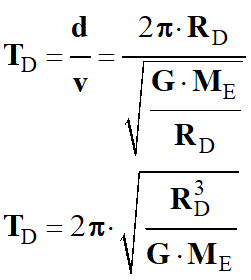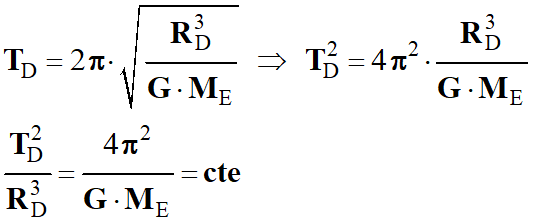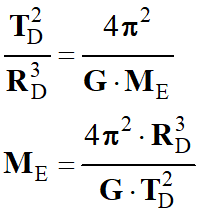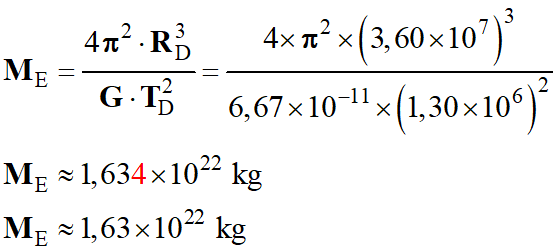Chap N° 13 Exercices 2024 : Mouvement dans un champ de gravitation.
|
Chap. N° 13
|
Mouvement dans un champ de gravitation
Exercices 2024
Cours.
Exercices
|
|
|
|
|
|
I-
Exercice :
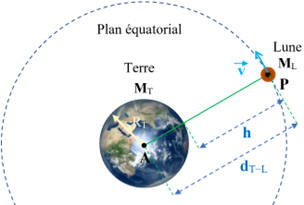
Face cachée de la Lune.
1)- Énoncé.
La face cachée de la lune, éclairée par le Soleil été
photographiée par le satellite Discover, situé à une distance
d'un million et demi de kilomètres de la Terre dans la direction du Soleil.
Les images ont été réalisées pendant le transit de la
Lune entre la Terre et le satellite.
DONNÉES :
-
Distance Terre-Lune :
dT-L =
3,84 × 105 km
-
1 j = 86164 s = 23 h 56 min 4 s
-
G = 6,67 × 10–11
m3 . kg–1
. s–2
-
MT =
5,98 × 1024 kg
-
RT
= 6400 km
-
ML =
7,34 × 1022 kg
b)-
Montrer que, dans le cadre de
l'approximation d'une orbite circulaire, la valeur
v
de la vitesse de la Lune sur son orbite autour de la Terre s'écrit :
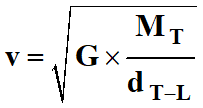
c)-
En déduire l'expression de la période de
révolution TL
de la Lune autour de la Terre, puis calculer sa valeur en seconde puis en jour.
d)-
La période de rotation de la Lune sur
elle-même est égale à 27,3 jours. Comparer cette valeur à
TL
et expliquer l'expression « face cachée de la Lune.

2)- Correction.
a)-
Expression et valeur
v
de la vitesse de la Lune sur son orbite autour de la Terre :
-
On étudie le mouvement du centre
de masse P
de la Lune, de masse
ML,
en orbite circulaire autour de la Terre.
-
La Terre est l’astre attracteur de
masse MT.
-
La Terre, corps à répartition
sphérique de masse se comporte comme un objet ponctuel de masse
MT.
-
La Lune est l’objet qui subit
l’attraction de la Terre.
-
Référentiel d’étude : Référentiel
géocentrique considéré comme galiléen.
-

-
Comme le mouvement est circulaire,
on utilise le repère de Frenet associé au référentiel géocentrique.
-
Repère de Frenet :
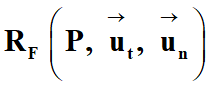
-
La Lune est soumise à la force de
gravitation exercée par la Terre :
-
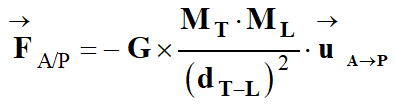
-
Schéma de la situation :
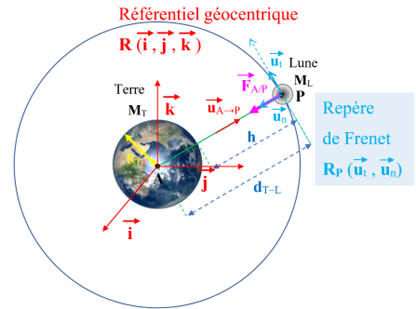
-
Expression de la force dans le
repère de Frenet :
-
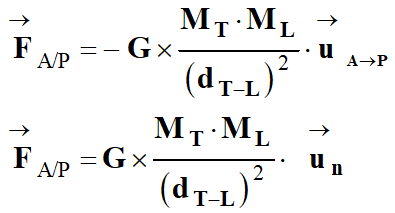
-
Le vecteur champ de gravitation
créé par la Terre au point
P de l’espace :
-
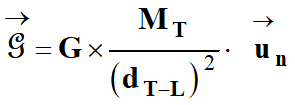
-
En conséquence :
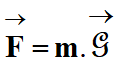
►
Caractéristiques du vecteur
accélération
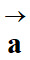 de
la Lune :
de
la Lune :
-
On applique la deuxième loi de
Newton au satellite :
-
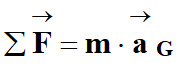
-
La Lune n’est soumise qu’à la
force de gravitation exercée par la Terre.
-
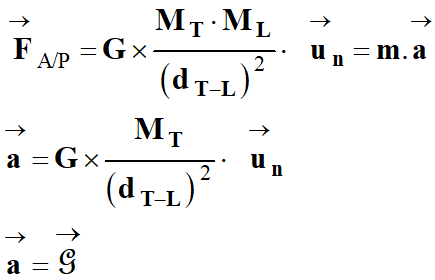
-
Le vecteur accélération
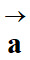 du
satellite a même direction, même sens et même valeur que le vecteur champ de
gravitation
du
satellite a même direction, même sens et même valeur que le vecteur champ de
gravitation
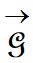 .
.
►
Caractéristiques du mouvement du
satellite :
-
Expression du vecteur accélération
dans le repère de Frenet
-
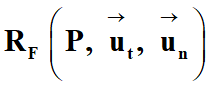
-
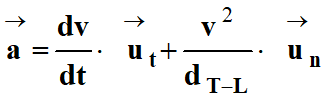
-
Avec :
-
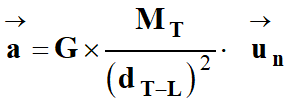
-
Il découle de ceci que :
-

-
Le mouvement du satellite est
circulaire uniforme dans le référentiel géocentrique.
-
D’autre part :
-
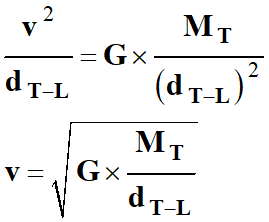
-
On retrouve le fait que
v
= cte, car G,
MT
et dT-L
sont des constantes.
►
Expression du vecteur vitesse
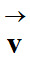 du satellite :
du satellite :
-
Le vecteur vitesse est tangent à
la trajectoire au point considéré :
-
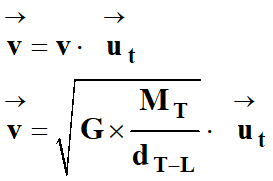
-
Schéma :
b)-
Expression de la période de révolution
TL
de la Lune autour de la Terre.
-
La période de révolution de la
Lune est la durée qu’elle met pour effectuer un tour autour de la Terre Soleil :
-
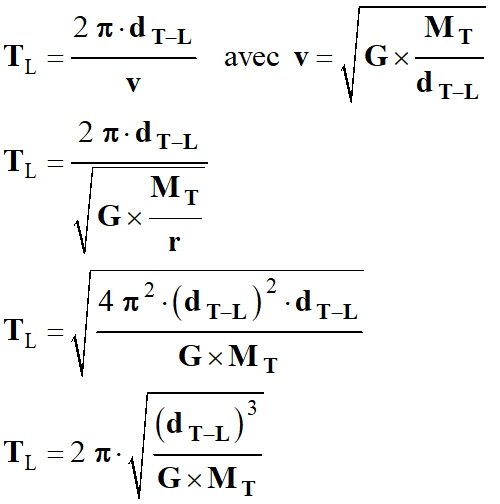
-
Valeur de
TL
en seconde puis en jour :
-
Application numérique :
-
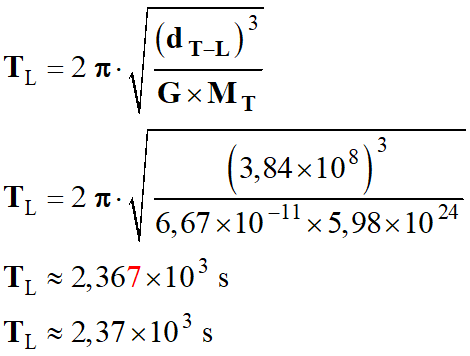
-
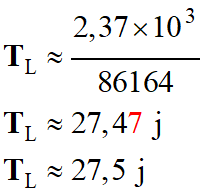
c)-
Comparaison avec
TL.
-
La période de rotation de la Lune
sur elle-même est égale à 27,3 jours.
-
La période de rotation de la Lune
sur elle-même est la même que sa période de révolution autour de la Terre.
-
Ainsi la Lune présente toujours la
même face à la Terre.
-
Cette face est appelée la face
visible, l’autre face, la face cachée.


-
La Lune est en rotation synchrone
avec la Terre.
https://fr.wikipedia.org/wiki/Orbite_de_la_Lune

II-
Exercice :
Satellites météorologiques.
1)- Énoncé.
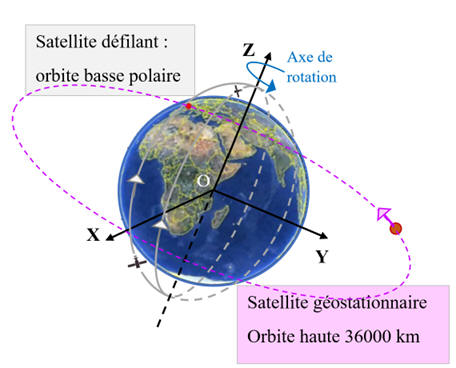
DOCUMENT : Satellites météorologiques.
Depuis 1960, les satellites météorologiques constituent
pour les services météorologiques une source d'information primordiale dans
leurs activités opérationnelles de suivi et de prévision du temps et du climat.
Il existe 2 familles de satellites météorologiques :
les satellites géostationnaires en orbite élevée - environ 35000 km - situé
au-dessus de l'équateur ;
les satellites défilants en orbite plus basse - environ 820 km - passant au
voisinage des pôles.
L'ensemble de ces satellites permet d'assurer une couverture complète et
continue de la planète.
D’après education.meteofrance.fr
Schéma :
Données :
1 j = 86164 s = 23 h 56 min 4 s
G
= 6,67 × 10–11 m3 . kg–1 . s–2
MT = 5,98 × 1024
kg
RT = 6380 km
a)-
Donner la définition
d'un satellite géostationnaire, préciser sa période de révolution
Tgéo et justifier que son
orbite est dans le plan de l'équateur.
b)-
Expliquer pourquoi la constellation de
satellite météorologiques géostationnaires doit être complétée par des
satellites défilants en orbite polaire.
c)-
Citer la 3e loi de Kepler et en déduire la
période de révolution Td
des satellites défilants.
d)-
Indiquer la durée au bout de laquelle un
satellite défilant repasse, dans le même sens, à la verticale du même point de
l'équateur.
e)-
En déduire l'intérêt de ces satellites pour
l'observation du globe.

2)- Correction.
a)-
Satellite
géostationnaire, préciser sa période de révolution
Tgéo.
-
Définition :
Satellite géostationnaire
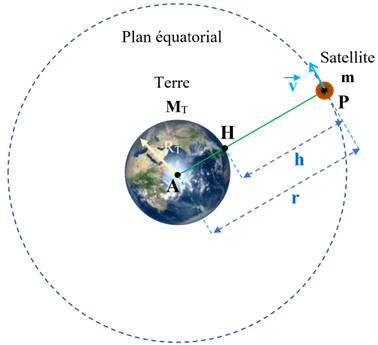
-
« Ces satellites sont
positionnés à la verticale d’un point de l’équateur et sont immobiles par
rapport à la surface de la Terre ».
-
Un satellite
géostationnaire est immobile dans un référentiel terrestre.
-
C’est pour cette
raison que l’on peut pointer une antenne dans sa direction.
-
Un satellite
géostationnaire est animé d’un mouvement circulaire dans le référentiel
géocentrique.
-
Dans ce cas, le
satellite modélisé par le point P reste toujours à la verticale du même
point H du globe.
-
Les points
A, H et P restent alignés au cours du temps.
-
Dans le
référentiel géocentrique la trajectoire d’un point
M est un cercle situé dans le plan
perpendiculaire à l’axe de rotation de la Terre.
Trajectoire sur la planète Terre
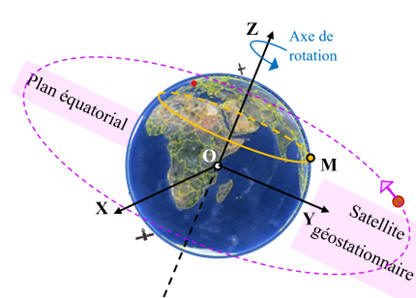
Satellite géostationnaire "animation"
-
Le plan de
l’orbite dans le référentiel géocentrique est le plan équatorial (plan xOy).
-
Période de
révolution Tgéo :
-
Le satellite
géostationnaire met la même durée que celle mise par la Terre pour effectuer un
tour autour de l’axe des pôles.
-
C’est la durée pour
effectuer un tour dans le référentiel géocentrique :
-
C’est la durée d’un
jour sidéral
-
Tgéo
= 1 j = 86164 s = 23 h 56 min 4 s
- Son
orbite
est dans le plan de l'équateur.
b)-
Constellation de
satellite météorologiques géostationnaires et satellites défilants en orbite
polaire.
►
Altitude de
révolution h d’un Satellite Géostationnaire :
-
Schéma de la situation :
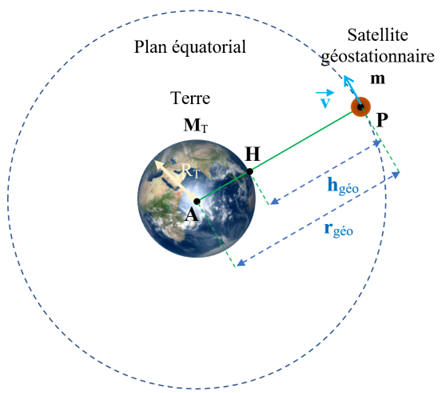
-
L’astre
central est la Terre de masse MT.
-
rgéo
= hgéo +
RT
-
Expression de
la période de révolution T :
-
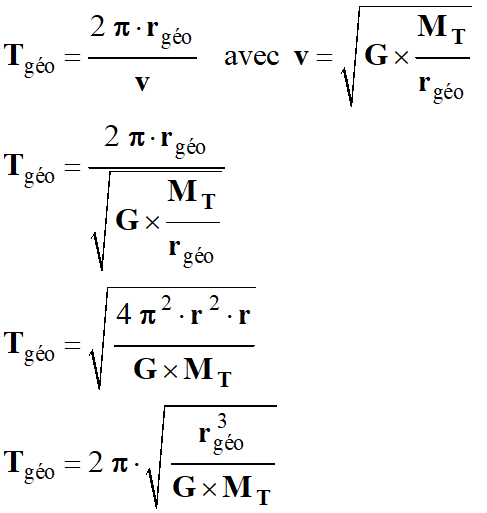
-
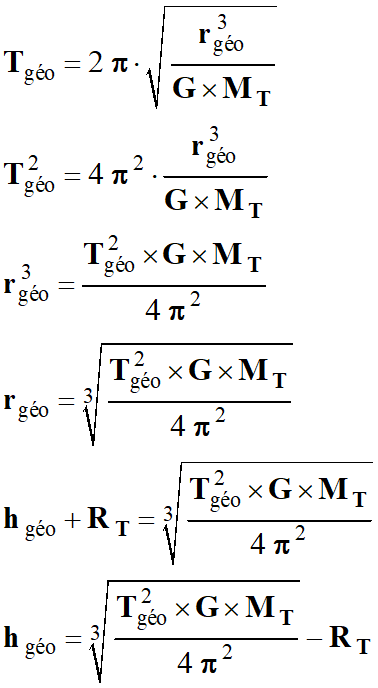
-
Application
numérique :
-
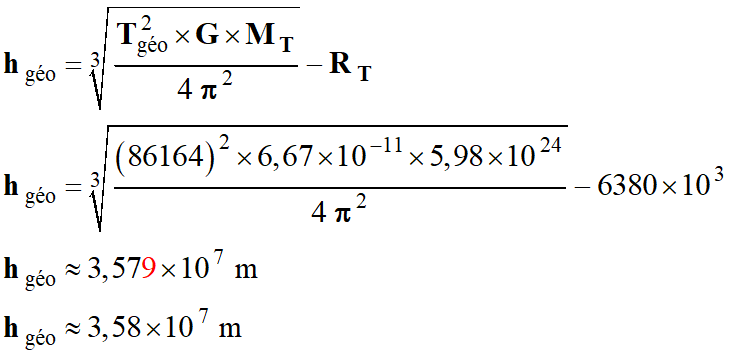
-
hgéo
≈ 3,58 × 107 m
-
hgéo
≈ 3,58 × 104 km
-
Les
satellites géostationnaires se déplacent sur une orbite très haute situé dans le
plan équatorial.
-
Ils peuvent ainsi
observer de vastes portions de la surface terrestre et aussi de l’atmosphère
terrestre.
-
Mais in ne peut pas
observer les régions polaires qui lui sont hors de portée.
-
Pour compléter
l’observation du globe terrestre, il est nécessaire d’utiliser des satellites à
orbite basse polaire.
c)-
Troisième loi de
Kepler et période de révolution Td
des satellites défilants.
|
 Pour toutes les planètes, le rapport
entre le cube du demi-grand axe a
de la trajectoire Pour toutes les planètes, le rapport
entre le cube du demi-grand axe a
de la trajectoire
et le carré de la période
T
de révolution est la même :

|
-
Cette constante ne dépend pas de la
masse de la planète.
-
Si la trajectoire est un cercle de
rayon r, on
peut écrire que :
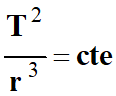
-
Cette constante peut être calculée.
-
Dans
le cas d’un satellite de la Terre :
-
La grandeur
T est la période de révolution du satellite autour de la Terre ;
-
La grandeur
a est la valeur du demi grand axe de
son orbite terrestre
-
Cette grandeur est
identique pour tous les satellites de la Terre (altitude :
hd = 820 km).
-
Période de révolution
Td des satellites défilants :
-
La période de
révolution d’un satellite est la durée qu’elle met pour effectuer un tour autour
de la Terre :
-
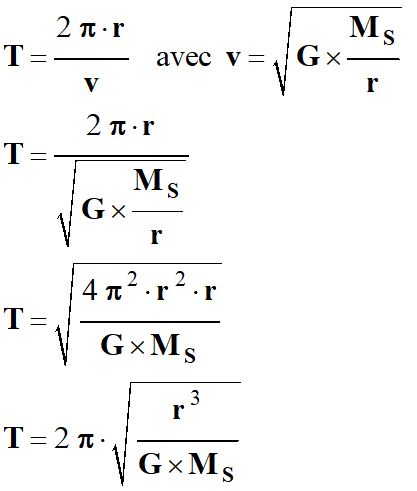
-
En élevant cette
expression au carré et en ordonnant, on peut écrire :
-
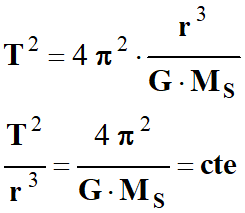
-
La constante
s’identifie à

-
Ainsi pour un
satellite géostationnaire :
-
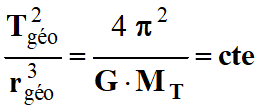
-
Pour un satellite
défilant :
-
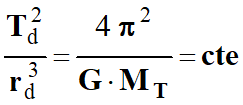
-
On peut utiliser la
relation suivante :
-
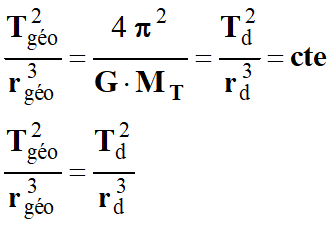
-
Avec :
-
hgéo
≈ 3,58 × 107 m
-
RT
= 6380 km
-
Tgéo
= 1 j = 86164 s = 23 h 56 min 4 s
-
rgéo
= RT + hgéo
-
rd
= RT + hd
-
hd
= = 820 km
-
Expression de
Td en fonction de
Tgéo :
-
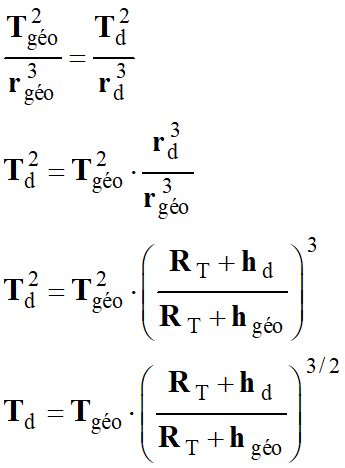
-
Application
numérique :
-
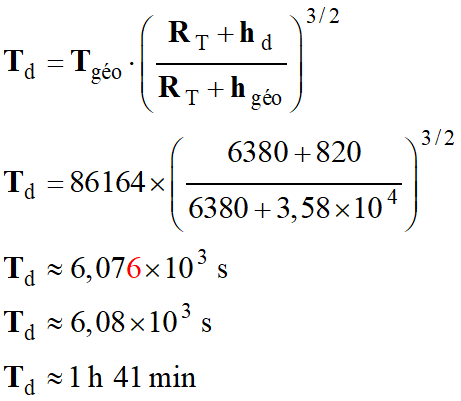
-
Autre méthode :
-
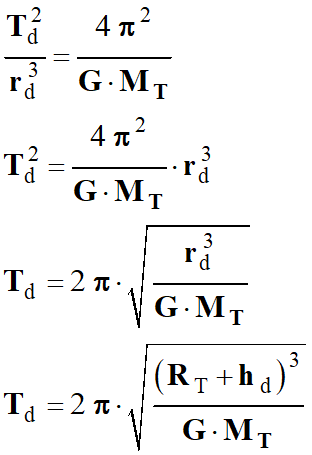
-
Application
numérique :
-
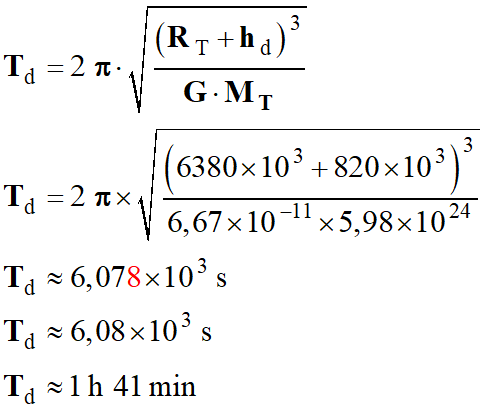
d)-
Durée au bout de laquelle un
satellite défilant polaire repasse, dans le même sens, à la verticale du même
point de l'équateur.
-
Dans le cas d’un
satellite défilant à orbite polaire :
-
La période de rotation
d’un tel satellite est :
-
Td
≈ 1 h 41 min = 101 min = 6,08 × 103 s
-
Au bout d’un tour
(durée Td), sa trace verticale s’est décalée d’un angle
α (rotation de la Terre) sur la
surface terrestre.
-
À cet angle
α est associée une distance
D à l'équateur :
-
TTerre
= 1 j = 86164 s = 23 h 56 min 4 s
-
Tableau :
|
Durée
|
Angle
|
|
TTerre
|
2 π
|
|
Td
|
α
|
-
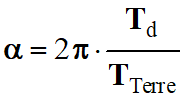
-
Expression de la
distance D :
-
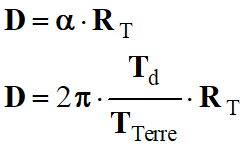
-
Application
numérique :
-
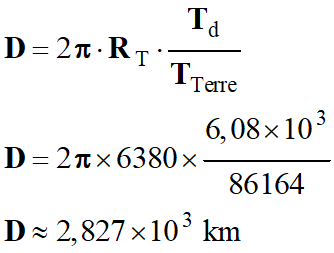
-
À l'équateur, les
traces successives du satellite au sol sont espacées de la distance
D :
-
D
≈ 2,827 × 103 km
-
Nombre
n de rotations du satellite pour que
les traces successives fassent le tour de l'équateur :
-
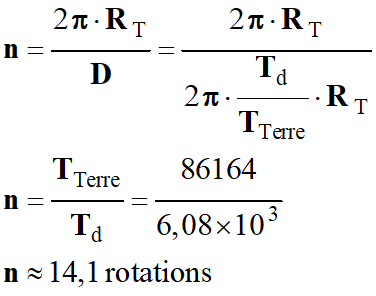
-
Durée
Δt au bout de laquelle un satellite
défilant repasse, dans le même sens, à la verticale du même point de
l'équateur :
-
Δt
= n .
Td = TTerre
-
Δt
≈ 1 j = 86164 s = 23 h 56 min 4 s
►
Cas du satellite
Jason-2 :
-
Altitude: Environ 1336
km.
-
Inclinaison orbitale:
66° (par rapport au plan équatorial)
-
L'orbite du satellite
Jason-2 est ajustée de façon qu'il survole exactement le même point d'origine
après 127 rotations.
-
Tjason
≈ 6,74 × 103 s ≈ 112 min ≈ 1,87 h ou 1 h 52 min
-
Durée
Δt au bout de laquelle un satellite
défilant repasse, dans le même sens, à la verticale du même point de
l'équateur :
-
Δt
= n .
Tjason ≈ 127 × 112
-
Δt
≈ 1,43 × 104 min
-
Δt
≈ 2,38 × 102 h
-
Δt
≈ 9,91 j
e)-
Intérêt de ces satellites
pour l'observation du globe.
-
Ces satellites
défilants polaires passent au-dessus de l'équateur à la même heure solaire
locale chaque jour.
-
Cela est utile pour
les satellites qui collectent des données sur la surface de la Terre.
-
Ils permettent
d’observer l’évolution quotidienne des différents phénomènes en ce point de la
surface et de l’atmosphère terrestre.
-
L’éclairement solaire
des lieux observés est pratiquement constant d’un cliché à l’autre (hors
incidence des saisons).
-
On parle d’orbites héliosynchrones pour ces
satellites.

III- Exercice :
Mission Rosetta.
1)- Énoncé.
En 2004, la sonde européenne Rosetta a
été lancée depuis la terre à destination de la comète 67P Churyumov -
Gerasimenko modélisée par une sphère de rayon R = 2,0 km.
DONNÉES :
Constante de gravitation :
G = 6,67 × 10–11 m3 . kg–1 . s–2
Masse de la comète 67P :
MC = 1,0 × 1013 kg
Masse de la sonde Rosetta :
mS = 3,0 × 103 kg
Distance Terre-Soleil :
dT-S = 1,00 unité astronomique = 1,00 ua.
1.
Comète 67P Churyumov –
Gerasimenko
DOCUMENT :
La comète 67P Churyumov – Gerasimenko a été découverte en septembre 1969.
Elle évolue sur une orbite elliptique dont le Soleil occupe l'un des foyers.
La valeur de la vitesse de la comète varie sur son orbite elliptique entre 5
et 35 km . s-1environ.

►
Distance au
plus près du Soleil (périhélie) : 1,24 ua
►
Distance la
plus loin du Soleil (aphélie) : 5,68 ua.
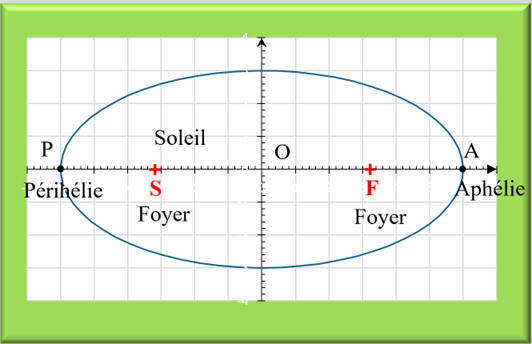
a)-
Représenter la
trajectoire de la comète précisant les positions du Soleil, de l'aphélie et du
périhélie.
b)-
Expliquer, en utilisant l'une des lois de
Kepler, pourquoi la valeur de la vitesse de la comète n’est pas constante sur sa
trajectoire.
On complétera le schéma précédent pour expliciter
la loi utilisée.
Préciser sur ce même schéma la position de la
comète pour laquelle la valeur de sa vitesse est la plus grande en justifiant la
réponse.
c)-
Rappeler la 3e loi de Kepler et en déduire
la valeur de la période de révolution de la comète.
2.
Satellisation de Rosetta
Au cours de l'année 2014, la sonde Rosetta est
arrivée à proximité de la comète et s'est placée en orbite circulaire autour de
celles-ci à une altitude h
de 20 km.
Le référentiel d'étude supposé galiléen, est le référentiel, dont
l'origine est le centre de la comète et dont les 3 axes pointent vers des
étoiles lointaines.
a)-
Réaliser un schéma de la sonde en orbite
autour de la comète en représentant le repère de Frenet associé à la sonde.
b)-
Donner dans le repère de Frenet les
coordonnées du vecteur
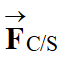 modélisant la force d'interaction gravitationnelle exercée par la comète sur la
sonde en fonction de G, mS,
MC, h et R, puis représenter cette force sur le
schéma.
modélisant la force d'interaction gravitationnelle exercée par la comète sur la
sonde en fonction de G, mS,
MC, h et R, puis représenter cette force sur le
schéma.
c)-
En supposant que la sonde est soumise
uniquement à l'interaction gravitationnelle avec la comète 67P établir dans le
repère de Frenet, les coordonnées de son vecteur accélération
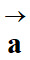 en fonction de G, MC, h et R.
en fonction de G, MC, h et R.
d)-
Montrer que dans l'approximation d'une
orbite circulaire, la valeur v de la
vitesse de la sonde a pour expression
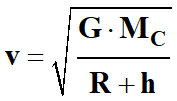 .
Calculer la valeur v de la vitesse
de la sonde sur son orbite.
.
Calculer la valeur v de la vitesse
de la sonde sur son orbite.
e)-
Exprimer puis calculer la durée
T d'un tour complet de la sonde
autour de la comète.
Chute de Philae

2)- Correction.
1.
Comète 67P Churyumov –
Gerasimenko
a)-
Schéma de la trajectoire de la comète.
-
Dans le référentiel héliocentrique, la trajectoire du
centre d’une planète est une ellipse dont le Soleil est l’un des foyers.
-
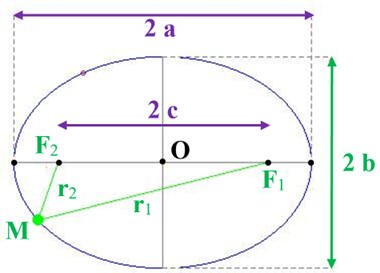
Définition d’une
ellipse :
Une ellipse est l’ensemble des points dont la somme des
distances à deux points fixes F1
et F2 (les foyers) est
une constante :
-
r1
+ r2 = 2
a.
-
Le grand axe de l’ellipse est égal à 2
a.
-
Le petit axe de
l’ellipse est égal à 2
b.
-
La distance entre les
deux foyers est 2
c.
-
F2
est le symétrique de F1 par rapport au centre O du
grand axe
-
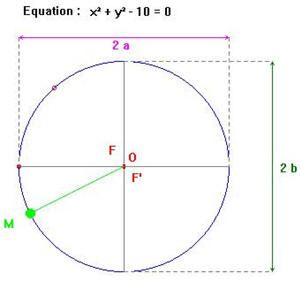
Remarque :
-
Un cercle est une
ellipse dont les deux foyers F1
et F2 sont confondus.
DS : Les Lunes de Saturne
-
Schéma :
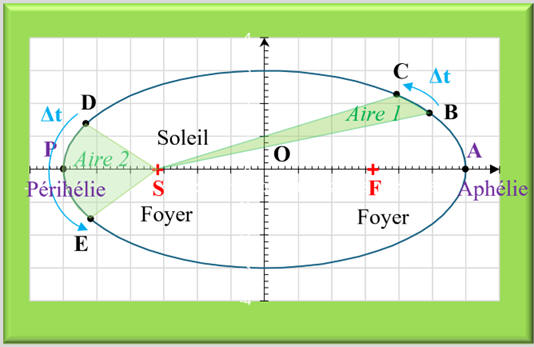
b)-
Schéma complété.
-
Deuxième
loi de Kepler : Loi des aires.
Les lois de Kepler
Loi
des Aires
-
Le segment de droite
qui relie le centre du Soleil au centre de la planète balaie des aires égales
pendant des durées égales.
-
Il résulte de ceci que
la planète se déplace plus vite lorsqu’elle se rapproche du Soleil.
-
En toute rigueur, le
mouvement d’une planète n’est pas uniforme.
-
La vitesse d’une
planète est plus grande au périhélie qu’à l’aphélie.
-
La vitesse de la
comète 67P est maximale au périhélie et minimale à l’aphélie.
c)-
Troisième loi de
Kepler et valeur de la période de révolution de la comète.
-
Troisième loi de Kepler : Loi des périodes :
|
 Pour toutes les planètes, le rapport
entre le cube du demi-grand axe a
de la trajectoire Pour toutes les planètes, le rapport
entre le cube du demi-grand axe a
de la trajectoire
et le carré de la période
T
de révolution est la même :

|
-
Cette constante ne dépend pas de la
masse de la planète.
-
Si la trajectoire est un cercle de
rayon r, on
peut écrire que :
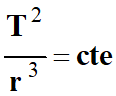
-
Cette constante peut être calculée.
-
Données :
►
Distance au plus près
du Soleil (périhélie) : 1,24 ua
►
Distance la plus loin
du Soleil (aphélie) : 5,68 ua.
-
On en déduit
que SP = 1,24 ua et
SA = 5,68 ua
-
En
conséquence : 2 a =
SP +
SA = 6,92 ua
-
La troisième loi de
Kepler permet d’écrire la relation suivante :
-
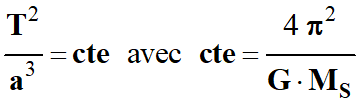
-
Quelques données :
-
Constante de
gravitation : G = 6,67 × 10–11 m3 . kg–1
. s–2
-
Masse de la
comète 67P : MC = 1,0 × 1013 kg
-
Masse de la
sonde Rosetta : mS = 3,0 × 103 kg
-
Distance
Terre-Soleil : dT-S = 1,00 unité astronomique = 1,00 ua.
-
Période de
révolution de la Terre autour du Soleil :
TT = 1,00 an
-
Comme la Terre et la
comète P67 gravitent autour du Soleil, on peut écrire la relation suivante :
-
Attention
pour la comète, il faut faire intervenir le demi grand axe
a / 2.
-
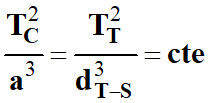
-
On en déduit
l’expression de la période TC
de la comète :
-
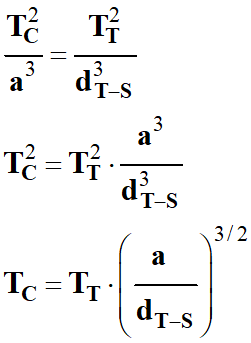
-
On exprime
a et dT-S dans la
même unité (ua) et
-
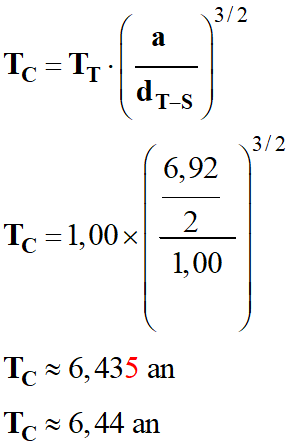
2.
Satellisation de Rosetta :
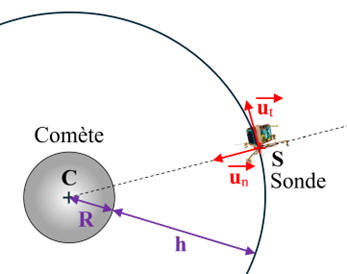
a)-
Schéma de la sonde en orbite autour de la
comète.
-
Repère de Frenet associé à la sonde :
b)-
Coordonnées du vecteur
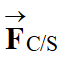 modélisant la force
d'interaction gravitationnelle.
modélisant la force
d'interaction gravitationnelle.
-
Repère de Frenet :
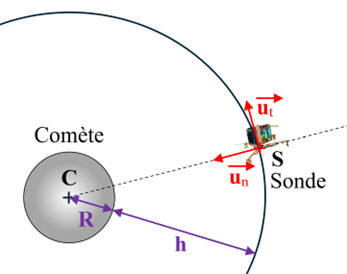
-
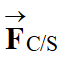 exercée par la comète sur la sonde en fonction de
G,
mS,
MC,
h et
R,
exercée par la comète sur la sonde en fonction de
G,
mS,
MC,
h et
R,
-
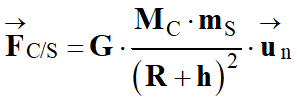
-
Coordonnées dans le
repère de Frenet :
-
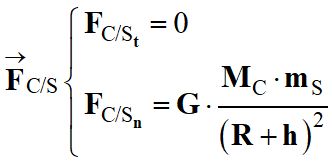
-
Représentation de cette force sur le schéma :
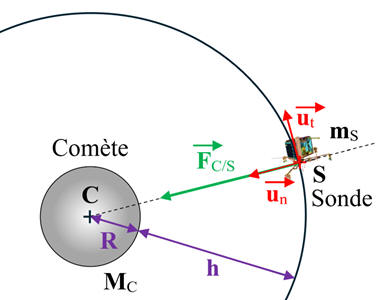
c)-
Coordonnées de son vecteur accélération
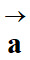 en fonction
de G,
MC,
h et
R.
en fonction
de G,
MC,
h et
R.
-
Système étudié : La sonde
S de masse
mS
-
Référentiel d’étude :
Référentiel cométocentrique supposé galiléen.
-
Repère de Frenet :
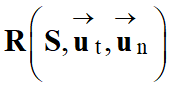
-
Bilan des forces :
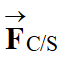
- Deuxième loi de Newton :
|
Dans un référentiel galiléen, la
somme des vecteurs forces 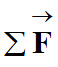
appliquées à un
système S, de masse m et de centre de masse G,
est égal au
produit de sa masse m par le vecteur accélération
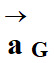
de son centre de
masse.
|
|
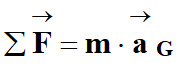
|
Valeur des
forces F en newton (N)
|
|
Valeur de la
masse m en kilogramme (kg)
|
|
Valeur de
l’accélération aG en mètre par
seconde au carré
(m . s–2)
|
-
Dans le cas présent :
-
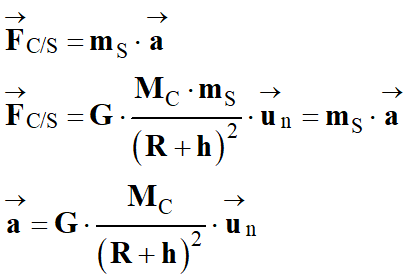
-
Le vecteur
accélération 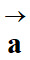 a même direction et même sens que le vecteur
a même direction et même sens que le vecteur
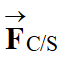 , c’est-à-dire que le
vecteur unitaire
, c’est-à-dire que le
vecteur unitaire
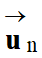 .
.
-
Coordonnées du vecteur
accélération
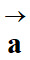 dans le repère de Frenet :
dans le repère de Frenet :
-
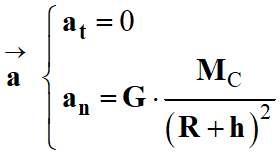
d)-
Valeur
v de la vitesse de la sonde.
-
Hypothèse :
approximation d'une orbite circulaire pour la sonde
-
On connait les
coordonnées du vecteur accélération :
-
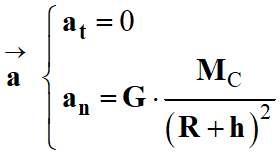
-
Avec :
-
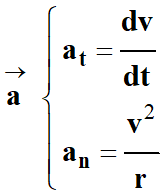
-
Comme
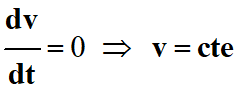
-
Le mouvement de la
sonde est circulaire uniforme :
-
D’autre part :
-
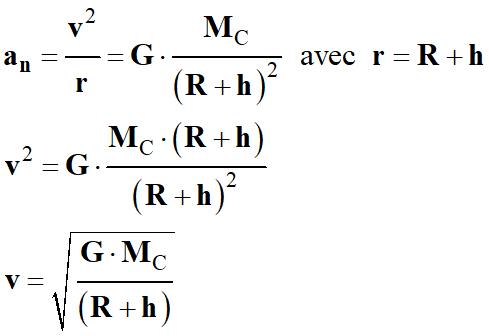
-
On retrouve bien
l’expression donnée dans l’énoncé.
-
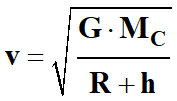 .
.
-
Données :
R = 2,0 km ;
altitude h = 20 km ;
MC
= 1,0 × 1013 kg ;
-
Valeur
v de la vitesse de la sonde sur son
orbite :
-
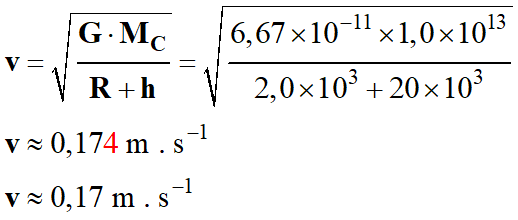
e)-
Durée
T d'un tour complet de la sonde
autour de la comète.
-
Expression de
T :
-
C’est la durée pour
effectuer un tour :
-
La distance parcourue :
d = 2 π
r = 2 π (R
+
h)
-
La sonde se déplace à
la vitesse constante v car son
mouvement est circulaire uniforme :
-
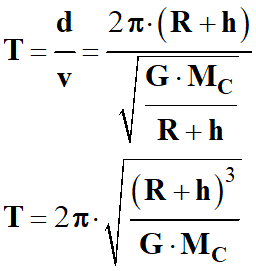
-
Calcul de la valeur de
T :
-
Application
numérique :
-
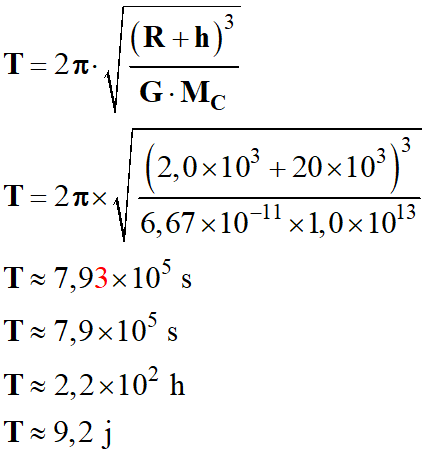

IV- Exercice :
Communication entre la Lune et Apollo.
1)- Énoncé.
À son arrivée au voisinage de la Lune, la
capsule Apollo est mise en orbite à une attitude h égale à 110 km.
Son mouvent est circulaire uniforme autour du centre de
la Lune.
Le module lunaire (LEM) est alors envoyé sur la Lune
avec deux astronautes à son bord.
Le troisième astronaute reste à bord de la capsule
Apollo.
Le schéma ci-dessous représente l'orbite du centre de
masse de la capsule Apollo autour de la lune.
Les échelles ne sont pas respectées.
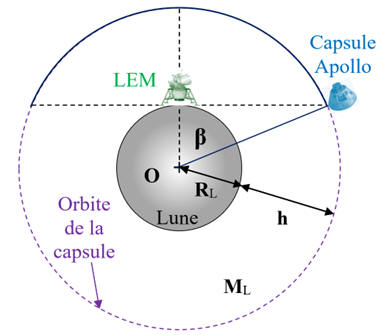
L’étude de mouvement de la capsule se fait dans le
référentiel lunocentrique supposé galiléen, défini par le centre de la Lune
supposée sphérique et 3 axes dirigés vers 3 étoiles fixes.
DONNÉES :
G =
6,67 × 10–11 m3 . kg–1 . s–2
Masse de la
Lune :
ML = 7,33 × 1022 kg
Rayon de la
Lune :
RL = 1,74 × 103 km
a)-
Expliquer
pourquoi la communication entre les astronautes sur la Lune et leur collègue
resté dans la capsule ne peut se faire que sur la partie de l'orbite en gras.
b)-
Déterminer la durée maximale de la
communication à chaque révolution de la capsule.

2)- Correction.
a)-
Explication pour la communication entre les
astronautes sur la Lune et leur collègue resté dans la capsule.
-
Les communications
entre la capsule Apollo et le module lunaire se font grâce aux ondes
électromagnétiques.
-
Les ondes
électromagnétiques se délacent dans le vide en ligne droite.
-
La capsule Apollo et
le LEM ne peuvent communiquer que si aucun obstacle n’est présent sur le trajet
des ondes électromagnétiques.
-
Ainsi la capsule Apollo et le LEM ne peuvent
communiquer que sur la partie en gras
de l’orbite de la capsule Apollo.
b)-
Détermination de la durée maximale de la
communication à chaque révolution de la capsule.
-
Le but est de
déterminée la durée Δt de la
communication.
-
Pour cela, on peut
calculer la longueur L de l’arc de
l’orbite concernée.
-
On utilise le fait que
la capsule Apollo est animée d’un mouvement circulaire uniforme.
-
On connaît la valeur
du rayon de la Lune RL et
l’altitude h de la capsule :
-
L
= 2 β × (RL +
h)
-
Avec :
-
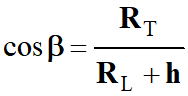
-
Et on peut déterminer
la valeur de l’angle β.
-
Maintenant, il faut
arriver à connaître la valeur de la vitesse
v de déplacement de la capsule.
-
Ainsi, on peut
déterminer la valeur de la durée de la communication :
-
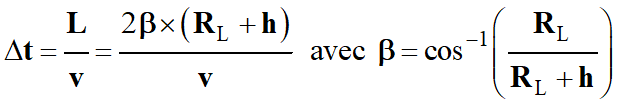
-
Pour accéder à la
vitesse, il faut passer par le vecteur accélération.
-
Pour accéder au
vecteur accélération, il faut utiliser la deuxième loi de Newton :
►
Étude dynamique :
-
Système étudié : la
capsule S de masse
mS
-
Référentiel d’étude :
Référentiel lunocentrique

-
Comme le mouvement est
circulaire, on utilise le repère de Frenet associé au référentiel géocentrique.
-
Repère de Frenet :
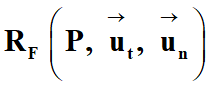
-
Schéma de la situation :
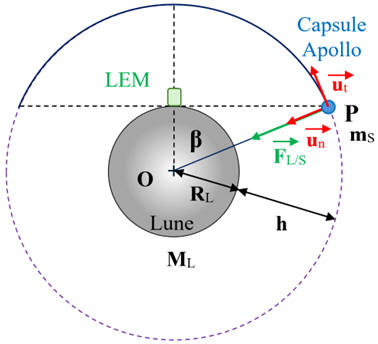
-
Bilan des forces :
force gravitationnelle exercée par la Lune sur la capsule Apollo
-
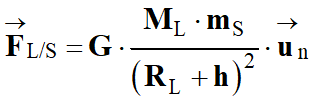
-
- Deuxième loi de Newton :
|
Dans un référentiel galiléen, la
somme des vecteurs forces 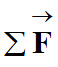
appliquées à un
système S, de masse m et de centre de masse G,
est égal au
produit de sa masse m par le vecteur accélération
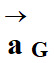
de son centre de
masse.
|
|
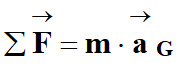
|
Valeur des
forces F en newton (N)
|
|
Valeur de la
masse m en kilogramme (kg)
|
|
Valeur de
l’accélération aG en mètre par
seconde au carré
(m . s–2)
|
-
Dans le cas présent :
-
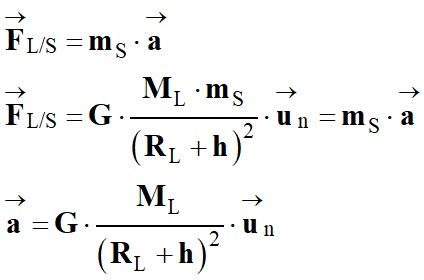
-
Le vecteur
accélération 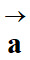 a même direction et même sens que le vecteur
a même direction et même sens que le vecteur
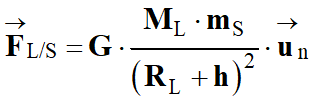 , c’est-à-dire que le
vecteur unitaire
, c’est-à-dire que le
vecteur unitaire
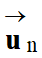 .
.
-
Coordonnées du vecteur
accélération dans le repère de Frenet :
-
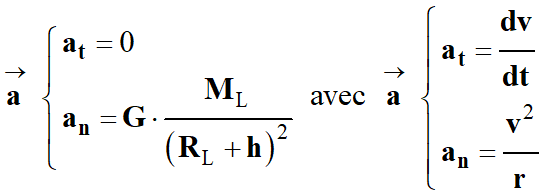
-
Expression de la
valeur de la vitesse v :
-
Or
r =
RL +
h
-
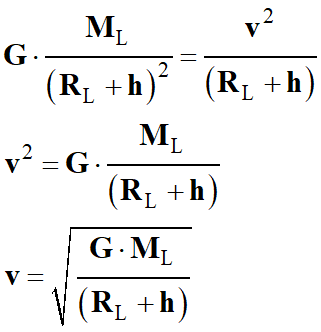
-
Durée maximale de
communication :
-
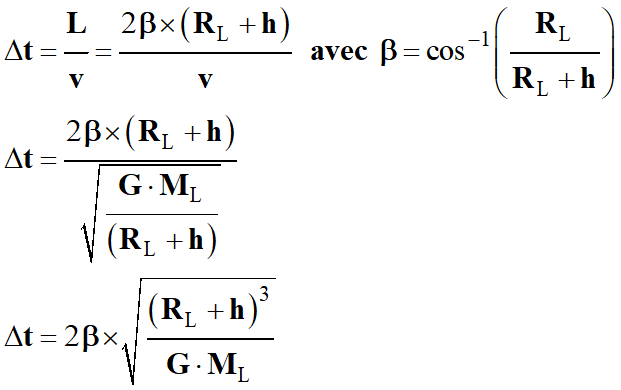
-
Valeur de l’angle
β : il faut exprimer
β en radian.
-
On peut exprimer les
distances en km.
-
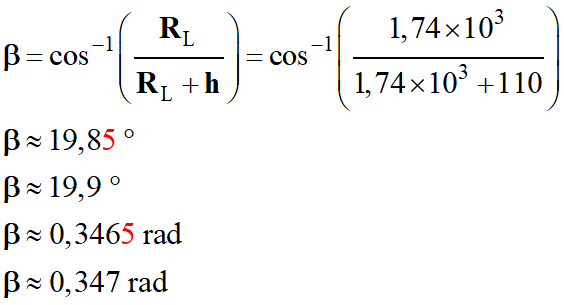
-
Application
numérique :
-
Il faut exprimer les
distances en mètres.
-
Il faut exprimer
β en radians.
-
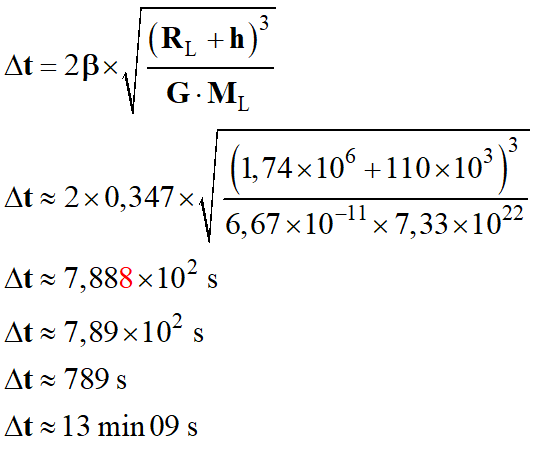

V-
Exercice :
De Hubble à James Webb.
1)- Énoncé.
En 2021, le télescope Hubble, qui tourne autour de la
terre depuis 1990, sera remplacé par le télescope James Webb.
Placé en permanence dans l'ombre de la Terre, le nouveau
télescope aura une position idéale pour observer le ciel.
DOC. 1
Télescopes spatiaux.
À l'inverse d'un télescope terrestre qui reçoit des
rayonnements filtrés par l'atmosphère, un télescope spatial n’est pas sensible
aux turbulences atmosphériques.
Le télescope spatial Hubble, du nom de l'astronome
américain Edwin Hubble (1889-1953) a été lancé en 1990.
D’une masse m
= 11 tonnes, il occupe une « orbite basse » à une altitude quasi constante
h = 600 km
de la surface de la Terre et fournit des images de l'Univers dans le domaine du
spectre ultraviolet, visible et proche infrarouge.
Le télescope spatial James Webb du nom d'un
administrateur de la NASA succédera au télescope Hubble en 2021.
Il sera placé à une distance proche de 1,5 million
de kilomètres de la Terre en un point d'un dénommé « point de Lagrange
L ».
D’après Wikipédia, hubblesite.org et jwst.nasa.gov.
DOC. 2
Points de Lagrange.
Le mathématicien sarde naturalisé français, Joseph-Louis
Lagrange (1736-1802) étudia le cas d'un petit corps, de masse négligeable,
soumis à l'attraction gravitationnelle de 2 corps massifs en orbite l'un par
rapport à l'autre.
Il montra qu’il existe 5 positions où le petit corps
reste immobile par rapport aux 2 autres sous l'action simultanée des champs de
gravitation des 2 corps massifs.
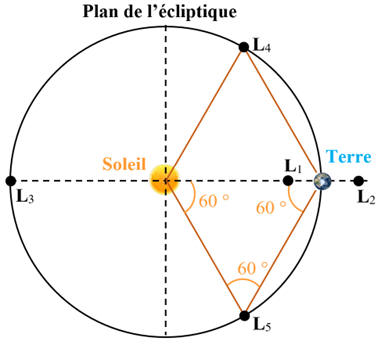
Ces positions sont appelées « points de Lagrange »
et sont notées de L1
à L5.
Dans le cas où les 2 corps sont en orbite circulaire,
ces points représentent les endroits où un troisième corps de masse négligeable
resterait immobile par rapport aux 2 autres :
Il accompagnerait à la même vitesse angulaire leur
rotation autour de leur centre de gravité commun sans que sa position par
rapport à eux n'évolue.
Schéma :
DONNÉES :
-
Distance Soleil-Terre :
d
= 149,6 × 106 km (équivaut à 1ua : 1 unité astronomique)
-
1 j = 86164 s = 23 h
56 min 4 s
-
G
= 6,67 × 10–11 m3 . kg–1 . s–2
-
M
T
= 5,97 × 1024 kg
-
RT
= 6370 km
Questions
Le système {télescope spatial Hubble} est étudié dans le
référentiel géocentrique en négligeant l'interaction gravitationnelle du Soleil
avec le télescope.
1.
Préciser la
trajectoire du centre de masse
M
du télescope Hubble dans ce référentiel.
2.
À
partir de la deuxième loi de Newton montrer que, dans l'approximation d'une
orbite circulaire, le mouvement du centre de masse
M
du télescope Hubble est uniforme.
3.
Montrer que l'expression de la valeur
v de la vitesse du
centre de masse M
du télescope Hubble dans leur référentiel géocentrique est :
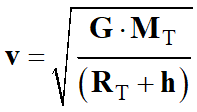
4.
Établir l'expression de la période de révolution
T
du télescope Hubble en fonction de RT
et h et
v.
5.
Rappeler la 3e
loi de Kepler et montrer qu'elle est vérifiée dans le cas du télescope Hubble.
6.
Calculer la
période de révolution
T
du centre de masse M
du télescope Hubble, exprimée en minute.
7.
On
envisage le cas où le télescope James Webb est positionné au point de Lagrange
L2.
Expliquer pourquoi le point L2
a été choisi pour l'orbite du télescope James Webb plutôt que le point
L1.

2)- Correction.
1.
Trajectoire du centre de
masse M
du télescope Hubble dans le référentiel géocentrique.
-
D’après le DOC.1, le
télescope spatial Hubble occupe une « orbite basse » à une altitude quasi
constante h = 600 km de la surface de
la Terre.
-
Le télescope Hubble décrit une orbite circulaire dans
le référentiel géocentrique.
2.
Caractéristiques
du mouvement du centre de masse
M
du télescope Hubble.
-
Le système {télescope
spatial Hubble} est étudié dans le référentiel géocentrique en négligeant
l'interaction gravitationnelle du Soleil avec le télescope.
-
Schéma de la situation :
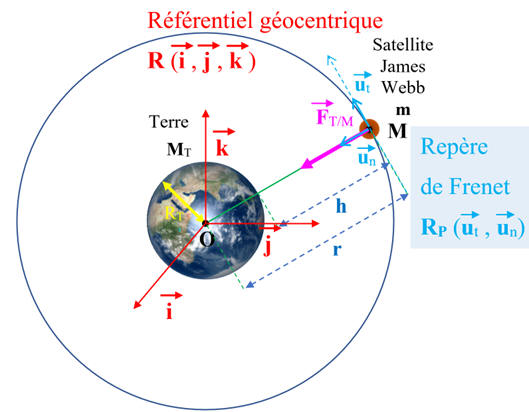
-
Système étudié
S = {télescope spatial Hubble} de masse
m = 11 t et de centre de masse
M.
-
Référentiel d’étude :
 Référentiel géocentrique supposé galiléen.
Référentiel géocentrique supposé galiléen.
-
Repère de Frenet :
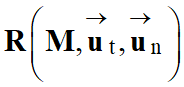
-
Bilan des forces :
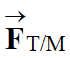 interaction gravitationnelle entre la Terre et le satellite.
interaction gravitationnelle entre la Terre et le satellite.
-
Deuxième loi de
Newton :
|
Dans un référentiel galiléen, la
somme des vecteurs forces 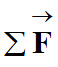
appliquées à un
système S, de masse m et de centre de masse G,
est égal au
produit de sa masse m par le vecteur accélération
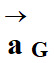
de son centre de
masse.
|
|
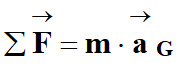
|
Valeur des
forces F en newton (N)
|
|
Valeur de la
masse m en kilogramme (kg)
|
|
Valeur de
l’accélération aG en mètre par
seconde au carré
(m . s–2)
|
- Dans le cas présent :
-
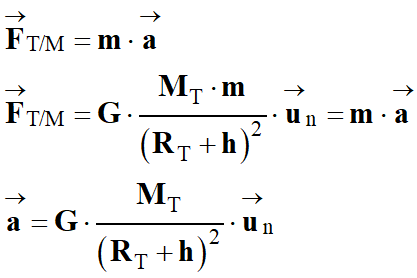
-
Le vecteur
accélération 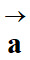 a même direction et même sens que le vecteur
a même direction et même sens que le vecteur
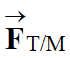 , c’est-à-dire que le
vecteur unitaire
, c’est-à-dire que le
vecteur unitaire
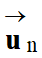 .
.
-
Coordonnées du vecteur
accélération dans le repère de Frenet :
-
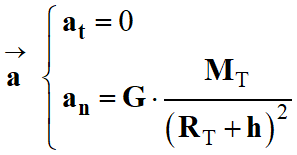
-
Avec :
-
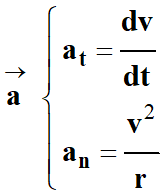
-
Comme
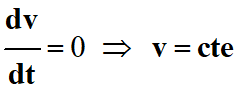
-
Le mouvement de la sonde est circulaire uniforme
3.
Expression de la
valeur v
de la vitesse du centre de masse M
du télescope Hubble dans leur référentiel géocentrique est :
-
D’autre part :
-
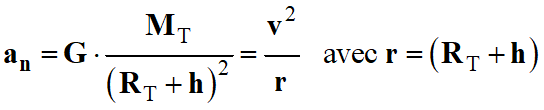
-
On en déduit la
relation suivante :
-
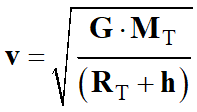
4.
Expression de la
période de révolution
T du télescope
Hubble en fonction de RT
et h et
v.
-
La période de
révolution d’un satellite est la durée qu’il met pour effectuer un tour autour
de la Terre :
-
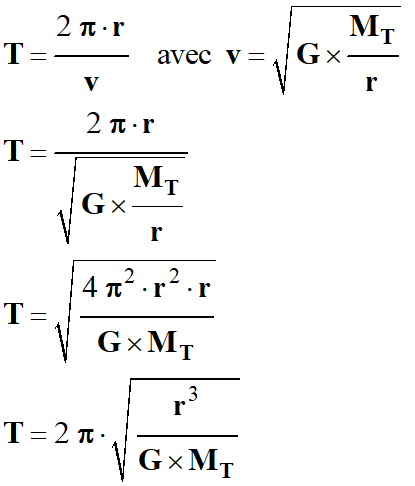
5.
Troisième loi de Kepler et
vérification dans le cas du télescope Hubble.
- Troisième loi de Kepler : Loi des périodes :
|
 Pour toutes les planètes, le rapport
entre le cube du demi-grand axe a
de la trajectoire Pour toutes les planètes, le rapport
entre le cube du demi-grand axe a
de la trajectoire
et le carré de la période
T
de révolution est la même :

|
-
Cette constante ne dépend pas de la
masse de la planète.
-
Si la trajectoire est un cercle de
rayon r, on
peut écrire que :
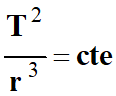
-
Cette constante peut être calculée.
-
Or :
-
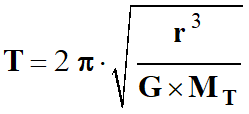
-
Si on élève cette
expression au carré et que l’on ordonne :
-
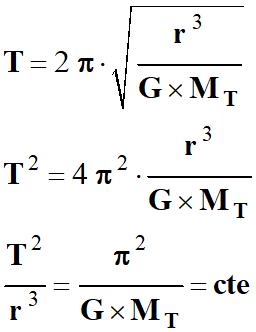
-
Relation valable pour tous les satellites de la
Terre.
6.
Période de révolution
T du centre de
masse M
du télescope Hubble en minute.
-
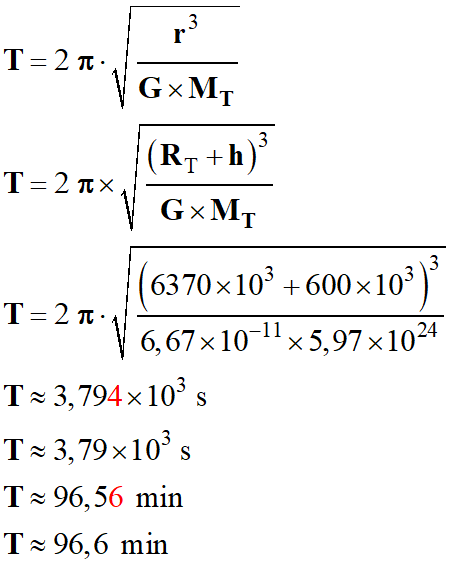
7.
Choix du point de Lagrange.
-
Le télescope James Webb est positionné au point de
Lagrange L2.
-
Schéma :

-
En position
L2,
il est a placé en permanence dans l'ombre de la Terre.
-
Le nouveau télescope a
une position idéale pour observer le ciel.
-
Il n’est pas gêné par la lumière solaire. Cela n’est
pas le cas de la position
L1.
-
Le point
L2 a
été choisi pour l'orbite du télescope James Webb plutôt que le point
L1
-
Il fournit des images
de l'Univers dans le domaine du spectre ultraviolet, visible et proche
infrarouge sans être gêné par la lumière solaire.

VI-
Exercice :
Un nouveau statut pour Pluton.
1)- Énoncé.
En 2006, Pluton a perdu son statut de
planète pour
devenir une planète naine.
Pourquoi la découverte d'Éris a -t-elle poussé les
astronomes à déclasser Pluton ?
DOC. 1
Éris et le changement de statut de son point
Pluton, découverte par l'astronome américain Clyde
Tombaugh (1906-1997) en 1930, était considérée comme la neuvième planète de
notre Système solaire.
Le 5 janvier 2005, une équipe d'astronomes a remarqué,
sur des photographies prises le 21 octobre 2003, un nouveau corps gravitant
autour du Soleil.
Provisoirement nommé 2003 UB 313, cet astre porte
maintenant le nom d'Éris, du nom de la déesse grecque de la discorde.
Au cours d'une assemblée générale, le 24 août 2006 à
Prague, 2500 astronomes de l'Union astronomique internationale (UAI)
ont décidé à main levée
de
déclasser
Pluton comme planète pour lui donner le
rang de « planète naine » en compagnie d’Éris et de
Cérès (gros astéroïde situé
entre Mars et Jupiter).
En effet, Pluton a une masse de 1,31 × 1022
kg, qui est 25 fois plus faible que la masse de Mercure, plus
petite planète actuelle du Système solaire.
Le
statut de
Pluton
(2)..
Photo de pluton :

DOC. 2
Éris
et Dysnomie
La planète naine Éris parcourt une orbite
elliptique autour du Soleil avec une période de révolution
TE
valant environ 557 années.
En 2005, les astronomes ont découvert qu’Éris possède un
satellite qui a été baptisé Dysnomie (télescope Keck II).
Dysnomie est un satellite naturel de la planète naine
Éris.
La représentation ci-dessous reproduit l'orbite de
Dysnomie autour d’Éris.
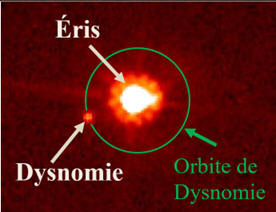
Le rayon de l'orbite de Dysnomie (orbite
considérée comme circulaire) est égal à RD
= 3,60 × 107 m
et la période de révolution de Dysnomie autour
d’Éris vaut TD
= 1,30 × 106 s.
Questions
1.
Question préliminaire : À partir des données du
DOC. 2
et en faisant différentes hypothèses, estimer la masse d’Éris.
2.
Problème : Justifier le
statut de « planète naine » donné à Pluton en compagnie de
Cérès et d' Éris.

2)- Correction.
1.
Question
préliminaire : Estimation de la masse d’Éris.
-
Les données
importantes du
DOC. 2 :
-
Rayon de l'orbite de
Dysnomie (orbite considérée comme circulaire) :
-
R
D
= 3,60 × 107 m
-
Période de révolution
de Dysnomie autour d’Éris :
-
TD
= 1,30 × 106 s
-
Schéma de la situation :
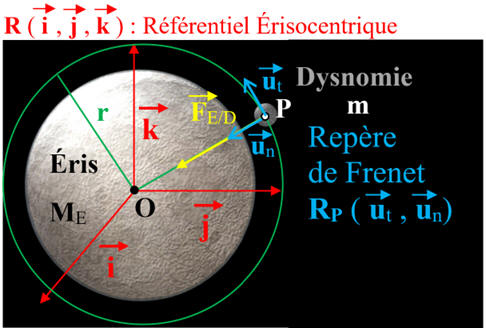
►
Cheminement du raisonnement :
-
Pour connaître la
masse ME d’Éris :
-
On utilise le fait que
Dysnomie est un satellite d’Éris :
-
Grâce à la deuxième
loi de Newton appliquée au système Dysnomie, on accède au vecteur accélération
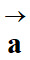 .
.
-
Par recherche de
primitive, on accède à la vitesse v du satellite Dysnomie autour d’Éris en
utilisant le repère de Frenet associé au satellite.
-
À partir de la vitesse v, on peut atteindre
l’expression de la période de révolution
TD
de Dysnomie.
-
Enfin, on utilise la
troisième loi de Kepler (Loi des périodes)
-
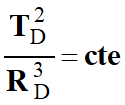 et la
masse ME d’Éris apparaît dans l’expression de la constante
cte.
et la
masse ME d’Éris apparaît dans l’expression de la constante
cte.
-
Comme l’on connaît les valeurs de
TD
et R
D,
on peut en déduire celle de ME.
►
Étude dynamique :
-
Système étudié : le satellite Dysnomie de masse
m
-
Référentiel d’étude :
Référentiel Érisocentrique supposé galiléen (voir le schéma).
-
Repère de Frenet :
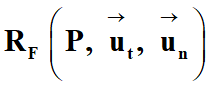
-
Bilan des forces :
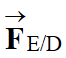 force gravitationnelle exercée par
Éris sur Dysnomie
force gravitationnelle exercée par
Éris sur Dysnomie
-
Deuxième loi de Newton :
|
Dans un référentiel galiléen, la
somme des vecteurs forces 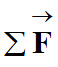
appliquées à un
système S, de masse m et de centre de masse G,
est égal au
produit de sa masse m par le vecteur accélération
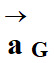
de son centre de
masse.
|
|
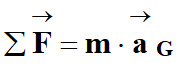
|
Valeur des
forces F en newton (N)
|
|
Valeur de la
masse m en kilogramme (kg)
|
|
Valeur de
l’accélération aG en mètre par
seconde au carré
(m . s–2)
|
-
Dans le cas présent :
-
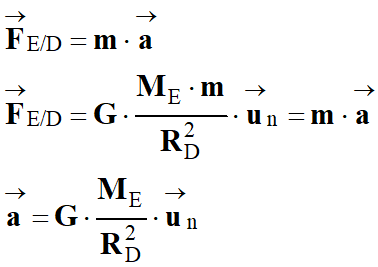
-
Le vecteur
accélération 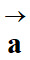 a même direction et même sens que le vecteur
a même direction et même sens que le vecteur
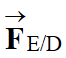 , c’est-à-dire que le
vecteur unitaire
, c’est-à-dire que le
vecteur unitaire
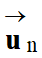 .
.
-
Coordonnées du vecteur
accélération
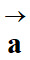 dans le repère de Frenet :
dans le repère de Frenet :
-
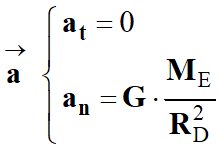
-
Hypothèse :
approximation d'une orbite circulaire pour Dysnomie
-
On connait les
coordonnées du vecteur accélération 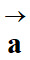 :
:
-
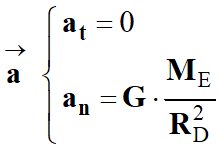
-
Avec :
-
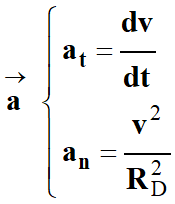
-
Comme
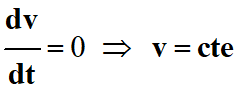
-
Le mouvement de
Dysnomie est circulaire uniforme :
-
D’autre part :
-
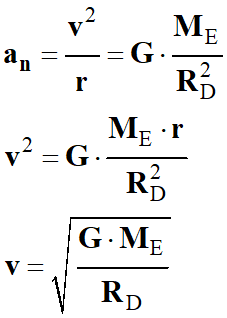
-
Durée
TD d'un
tour complet de la sonde autour
d’Éris.
-
Expression de la période
TD :
-
C’est la durée pour
effectuer un tour :
-
La distance parcourue :
d
= 2 π RD
-
Dysnomie se déplace à la vitesse constante
v
car son mouvement est circulaire uniforme :
-
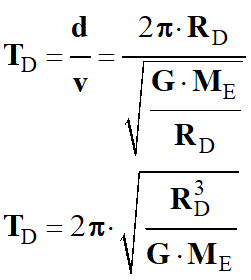
-
On utilise la
troisième loi de Kepler :
-
Troisième loi de
Kepler : Loi des périodes :
|
 Pour toutes les planètes, le rapport
entre le cube du demi-grand axe a
de la trajectoire Pour toutes les planètes, le rapport
entre le cube du demi-grand axe a
de la trajectoire
et le carré de la période
T
de révolution est la même :

|
-
Cette constante ne dépend pas de la
masse de la planète.
-
Si la trajectoire est un cercle de
rayon r, on
peut écrire que :
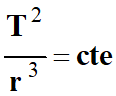
-
Cette constante peut être calculée.
-
Dans le cas d’un
satellite d’Éris :
-
La troisième loi de
Kepler permet d’écrire la relation suivante :
-
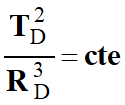
-
Pour retrouver cette relation, il faut élever
l’expression de la période
T
D trouvée
précédemment au carré.
-
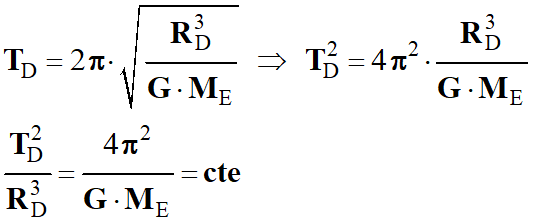
-
Connaissant les valeurs de
TD
et RD,
on peut en déduire celle de ME.
-
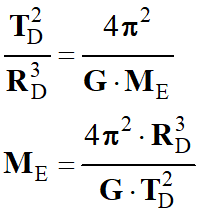
-
Application
numérique :
-
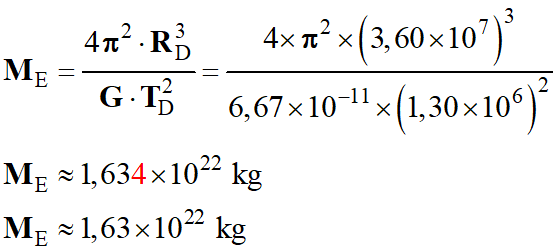
2.
Problème :
Justification du statut de « planète naine » donné à Pluton.
-
Mercure est la première planète du système solaire,
mais également la plus petite
:
-
Masse de Mercure :
M
Mercure
= 3,285 × 1023 kg (environ la moitié de la masse de la Terre)
-
Masse de Pluton :
-
MPluton
=1,29
× 1022 kg
-
La masse de Pluton est
environ 25 fois plus petite que celle de Mercure et environ 50 fois plus petite
que celle de la Terre.
-
Distances :
-
Distance Pluton-Soleil
dP-S =
5,913 x 109 km
-
Distance Terre-Soleil
dT-S =
1,496 × 108 km
-
D’autre part, Pluton
est 40 fois plus loin du Soleil que la Terre.
-
On remarque qu’Éris a
une masse légèrement plus grande que celle de Pluton.
-
Si on considère que
Pluton est une planète, il en va de même pour Éris.
-
Cela va avoir un
impact important sur notre Système solaire et on va devoir changer tous les
manuels.
-
Pour ne pas avoir à
modifier tous les manuels traitant du système solaire à chaque nouvelle
découverte d’un gros astéroïde, les scientifiques ont décidé (24 août 2006) de
déclasser
Pluton.
-
Pluton est ainsi
passée du statut de planète à celui
de planète naine.
-
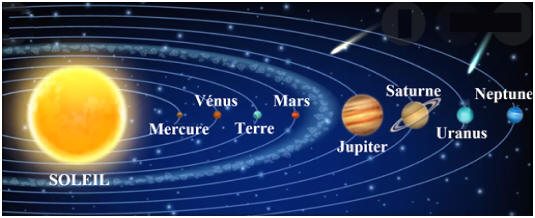
Le Système solaire
comprend huit planètes.
Système Solaire
-
Le nombre de planètes naines risque d’augmenter au
cours des découvertes grâce à l’évolution des télescopes d’observations.
Pour se promener dans le Système Solaire :
 Stellarium
Stellarium
 Celestia
Celestia

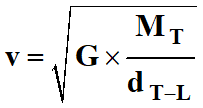

![]()
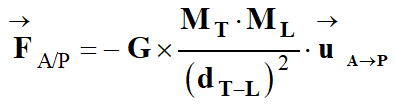

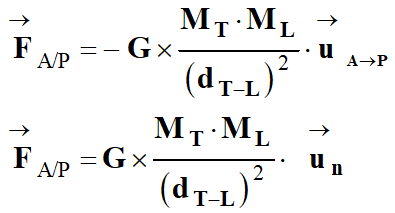
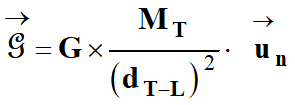
![]()
![]() de
la Lune :
de
la Lune : ![]()
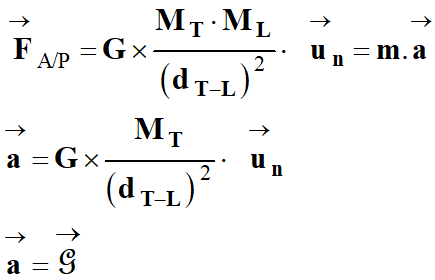
![]() du
satellite a même direction, même sens et même valeur que le vecteur champ de
gravitation
du
satellite a même direction, même sens et même valeur que le vecteur champ de
gravitation
![]() .
.![]()
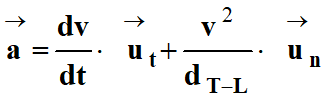
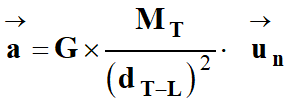
![]()
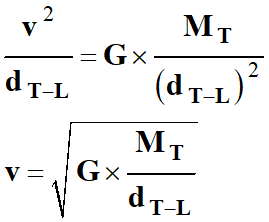
![]() du satellite :
du satellite :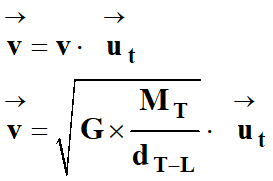

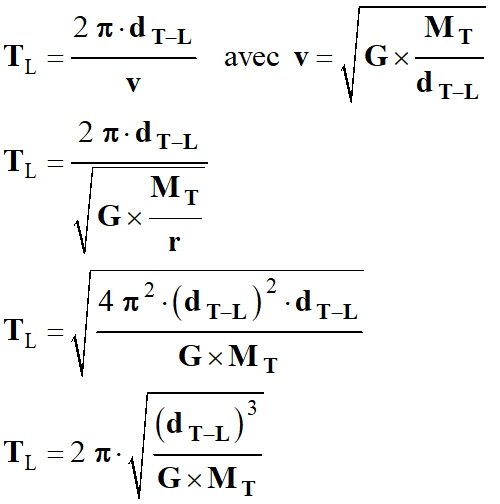
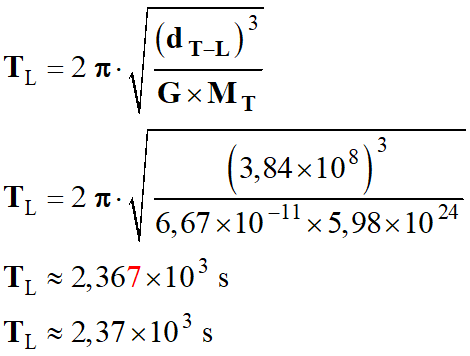
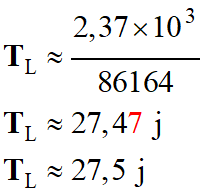






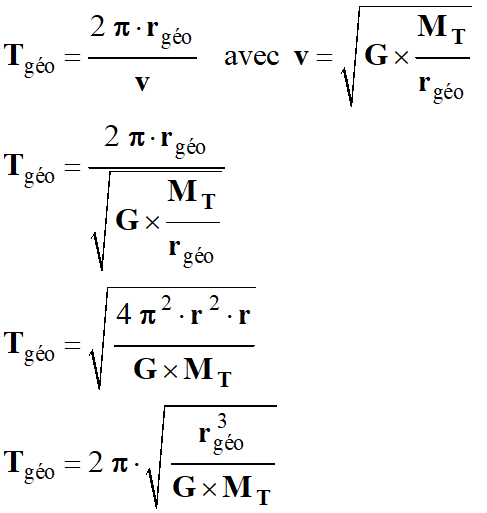
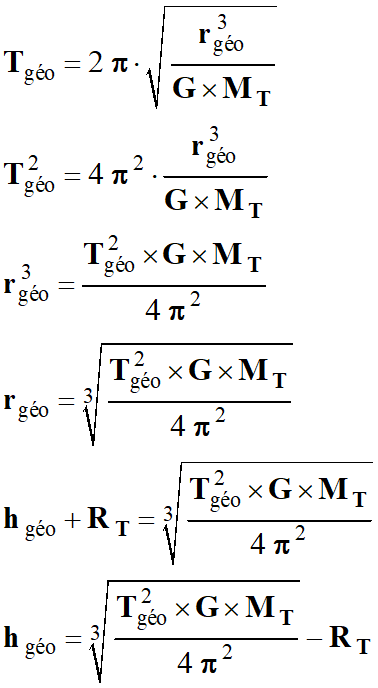
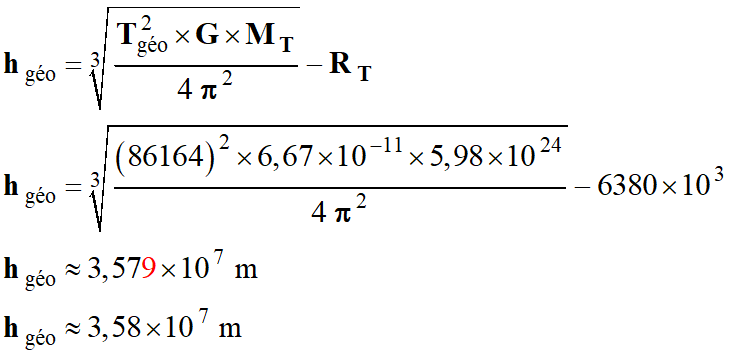

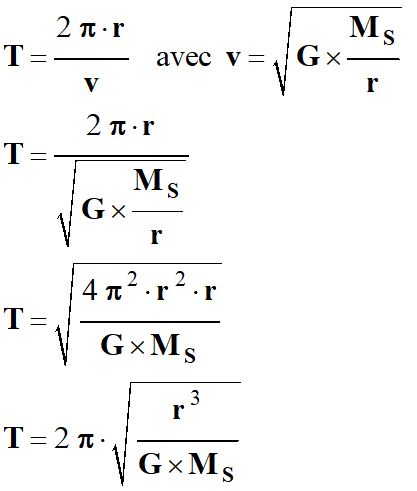
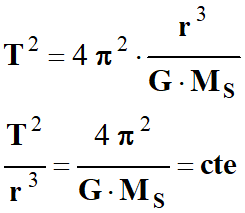

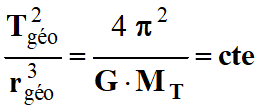
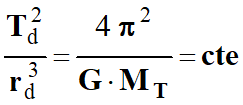
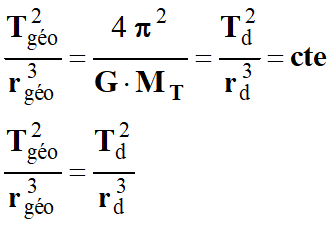
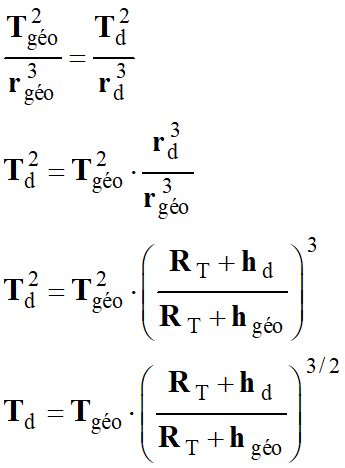
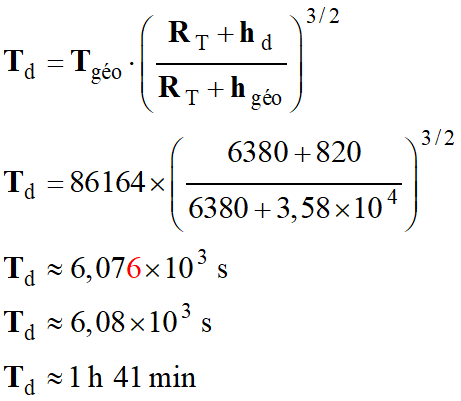
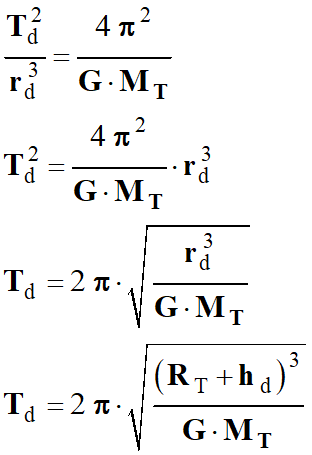
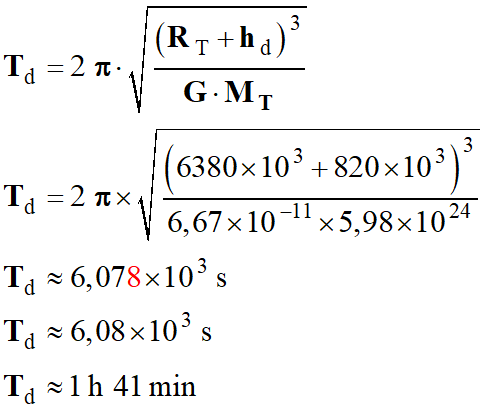
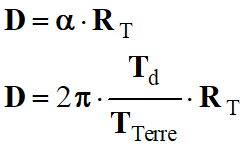
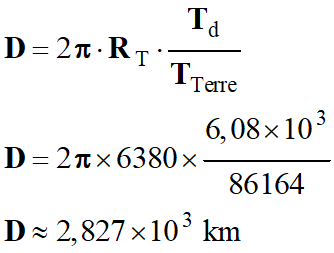


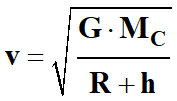 .
Calculer la valeur v de la vitesse
de la sonde sur son orbite.
.
Calculer la valeur v de la vitesse
de la sonde sur son orbite.