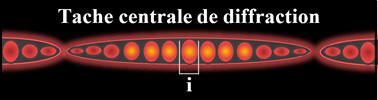
DS N° 02 : Les fentes de Young (30 min)
1.
Conditions pour observer une figure
d’interférences :
-
Cas des fentes de Young :
-
Pour observer une figure d’interférences
avec de la lumière, il faut éclairer les deux fentes avec une unique
source de lumière monochromatique.
-
Les deux fentes étroites se comportent
comme des sources lumineuses synchrones et en phase.
-
Pour observer des interférences avec des
sources lumineuses, il faut que les deux sources soient ponctuelles,
synchrones et en phase.
2.
Interférences constructives et destructives
a.
Condition pour obtenir une frange brillante au
point P :
-
Schéma de la situation :
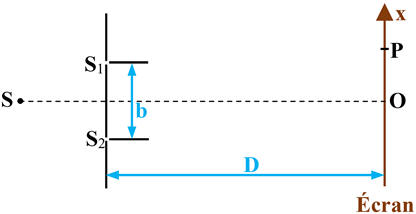
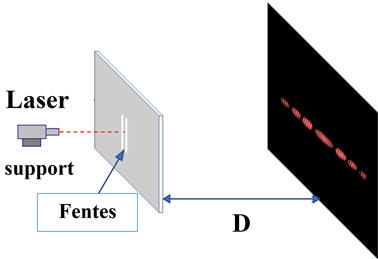
-
Distance entre le dispositif et l’écran :
-
D = 1,50 m
-
Distance entre les deux fentes S1
et S2 de ce dispositif :
-
b
= 0,20 mm
-
En un point P de l’écran
d’abscisse xk,
-
Différence de chemin optique ΔL
des rayons issus de S1 et S2 :
- 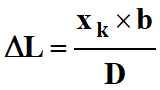
►
Interférences constructives :
-
Si
ΔL = k .
λ0 avec k €
ℤ
-
Les ondes arrivent en phase au point
considéré.
-
Les interférences sont constructives.
-
On observe une frange brillante.
►
Interférences destructives :
-
Si
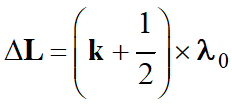 avec
k €
ℤ
avec
k €
ℤ
-
Les ondes arrivent en opposition de phase
au point considéré.
-
Les interférences sont destructives.
-
On observe une frange sombre.
-
Comme on veut observer une frange
brillante au point P :
-
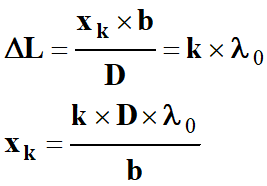 avec
k €
ℤ
avec
k €
ℤ
b.
Expression de l’interfrange i.
-
Lors d’interférences lumineuses,
l’interfrange, notée i, est
la distance séparant deux franges brillantes consécutives ou deux
franges sombres consécutives.
-
i
= xk+1 – xk
-
Prenons le cas de deux franges brillantes
consécutives :
-
ΔLk
= k .
λ0 et
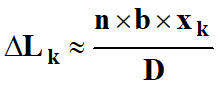
-
ΔLk+1
= (k + 1) . λ0 et
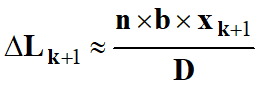
-
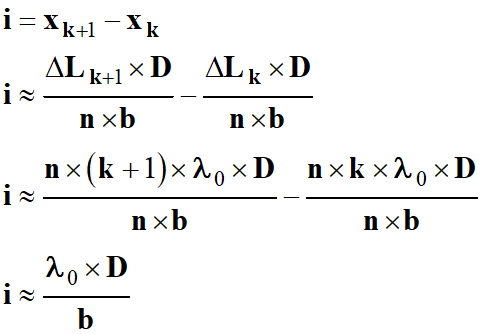
-
L’interfrange
i est donnée par la relation suivante :
|
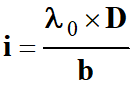
|
|
i
|
Interfrange en mètre (m)
|
|
λ0
|
Longueur d’onde de la radiation dans le vide en mètre (m)
|
|
D
|
Distance des sources lumineuses à l’écran en mètre (m)
|
|
b
|
Distance entre les deux sources lumineuses en mètre (m)
|
c.
Nombre maximal
de franges brillantes observables sur l’écran
-
Largeur de l’écran :
-
ℓ = 10 cm
-
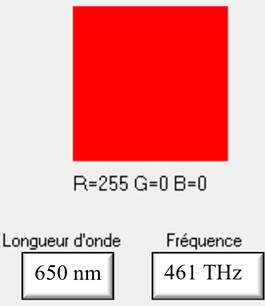
Longueur d’onde de la
radiation
-
λ0 = 650 nm,
-
Distance entre le dispositif et l’écran :
-
D = 1,50 m
-
Distance entre les deux fentes S1
et S2 de ce dispositif :
-
b
= 0,20 mm
-
Valeur de l’interfrange
i :
-
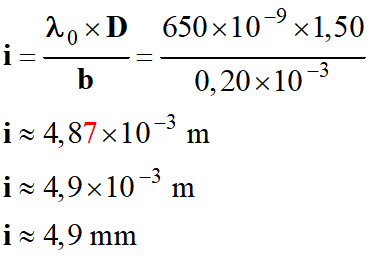
-
Au phénomène de diffraction se superpose
le phénomène d’interférence.
-
On peut calculer la valeur de l’angle
caractéristique dans le cas d’une seule fente :
-
Lorsqu’un faisceau parallèle de lumière
de longueur d’onde λ traverse une fente de largeur
a,
l’écart angulaire θ, entre le centre de la tache centrale
et la première extinction est donné par
la relation suivante :
|
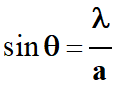
|
|
θ
|
Écart
angulaire en radian (rad)
|
|
λ
|
Longueur
d’onde en mètre (m)
|
|
a
|
Largeur
de l’ouverture rectangulaire
|
-
Si le rapport
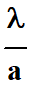 est petit, on peut faire
l’approximation suivante :
est petit, on peut faire
l’approximation suivante :
-
sin
θ ≈
θ (rad) :
-
la relation s’écrit alors :
|
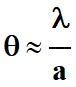
|
|
θ
|
Écart
angulaire en radian (rad)
|
|
λ
|
Longueur
d’onde en mètre (m)
|
|
a
|
Largeur
de l’ouverture rectangulaire
|
-
Pour la largeur de la fente, on prend :
a = 20 μm
-
Dans le cas présent :
-
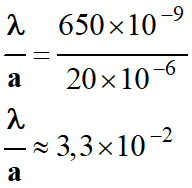
-
On peut utiliser l’approximation sin
θ ≈
θ (rad).
-
Cette relation permet de déterminer
expérimentalement la longueur d’onde λ de la lumière d’un
faisceau connaissant la largeur de la fente.
-
Dans le cas ou D >> L
(largeur de la tache
centrale), on peut déterminer la relation donnant la largeur de
la tache centrale L
en fonction de la longueur d’onde λ0 et de la largeur
a
de la fente.
-
On fait l’approximation des petits
angles.
-
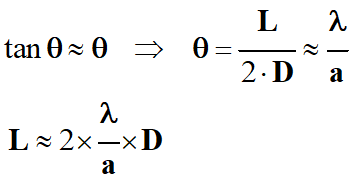
-
Largeur
L de la tache centrale de
diffraction :
-
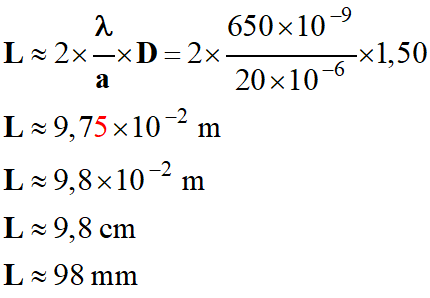
-
Nombre maximal
Nmax de franges brillantes visibles sur l’écran :
-
La largeur de l’écran est ℓ = 10
cm
-
L’interfrange est
i ≈ 4,9 mm
-
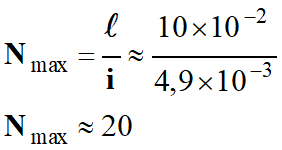
-
Remarque :
-
Comme la frange centrale est brillante,
on peut observer 19 franges brillantes
-
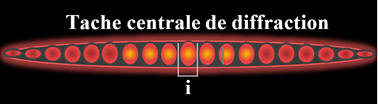
Pour :
a = 20 μm, tache centrale :
L = 9,8 cm
-
Pour a = 30 μm, la tache centrale
L = 6,5 cm