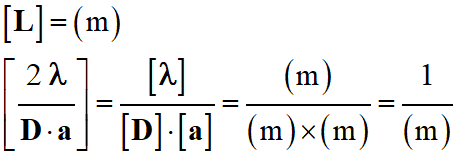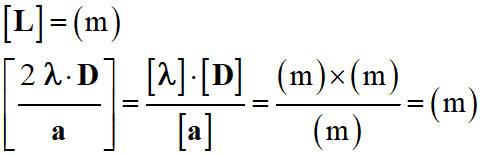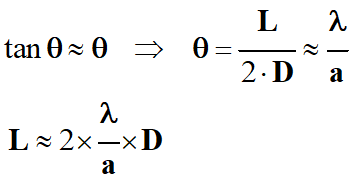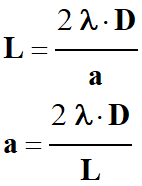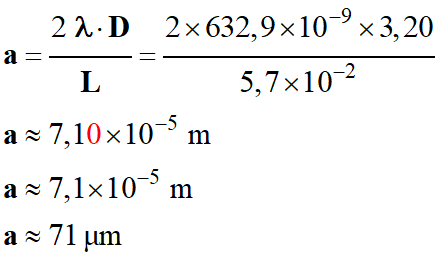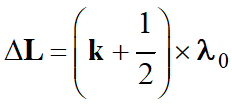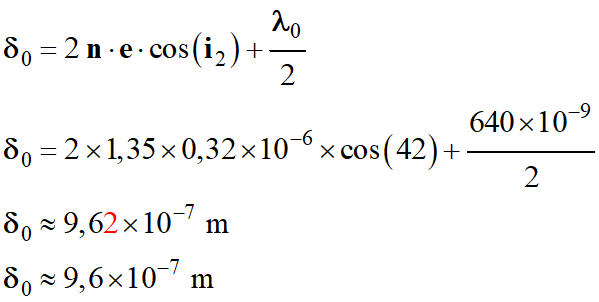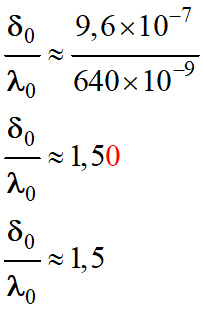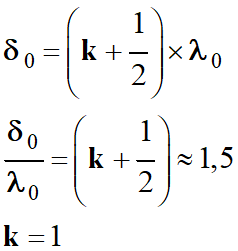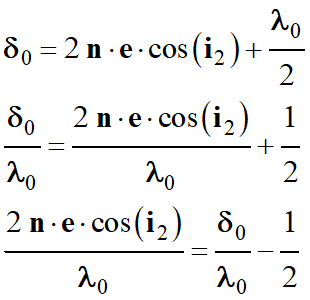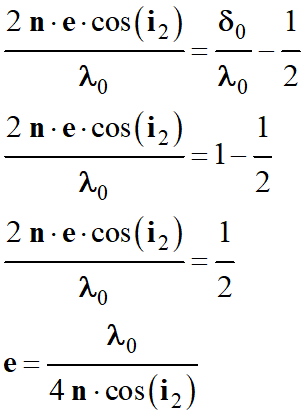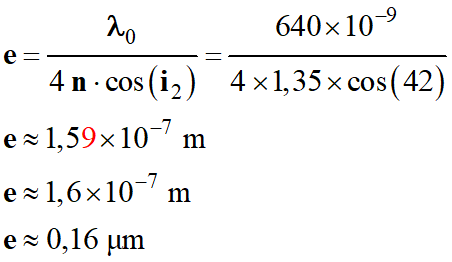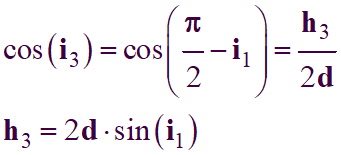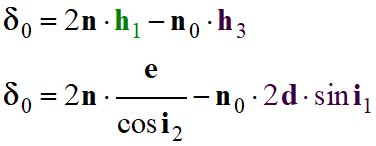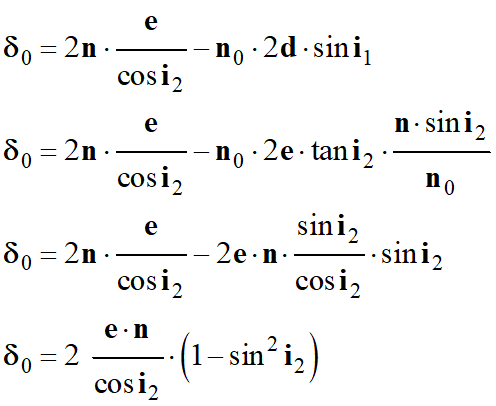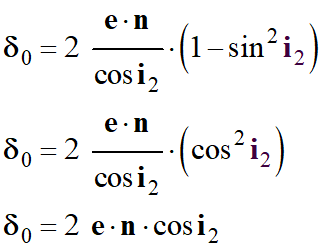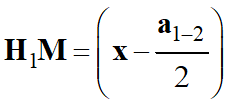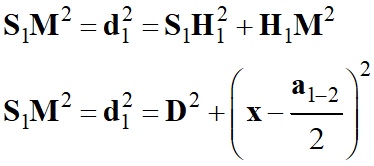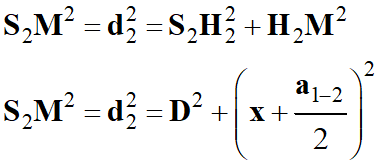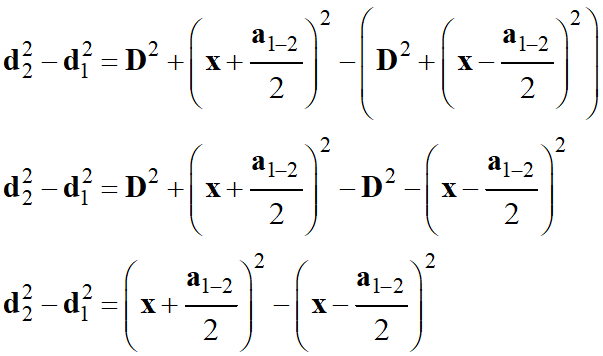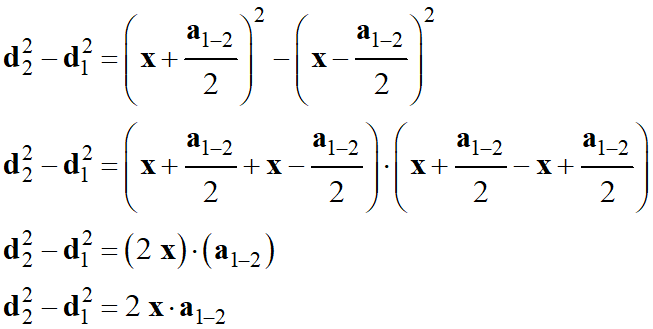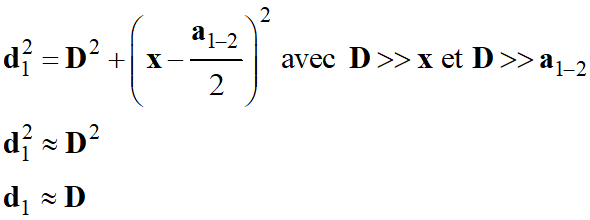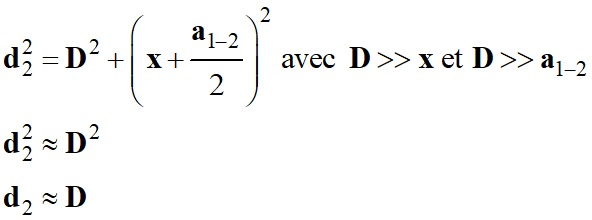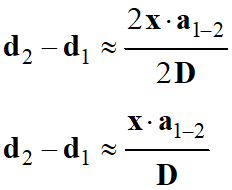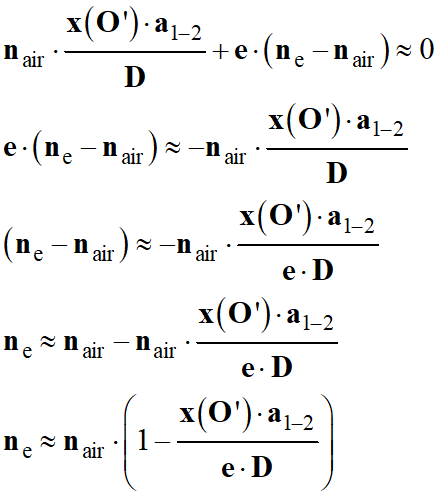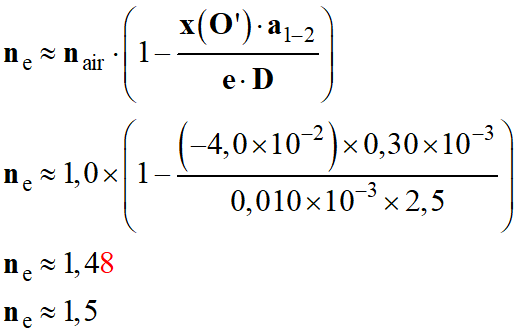Chap. N° 18 Exercices 2024 : Diffraction et interférences
|
Chap. N°18
|
Diffraction et interférences
Exercices 2024
Cours
Exercices
|
|
|
|
|
|
I-
Exercice :
Mesurer une fissure .
1)- Énoncé.
Une plaque fissurée est placée sur le trajet du faisceau émis
par un laser de longueur d'onde λ
= 632,9 nm.
On souhaite mesurer la largeur a
de la fissure.
On enregistre l'intensité lumineuse reçue le long d'un axe
horizontal sur un écran perpendiculaire au faisceau du laser, placé à une
distance D = 320 cm après la
fissure.
On obtient la courbe présentée ci-dessous qui permet de
déterminer la largeur L de la
tache de diffraction.
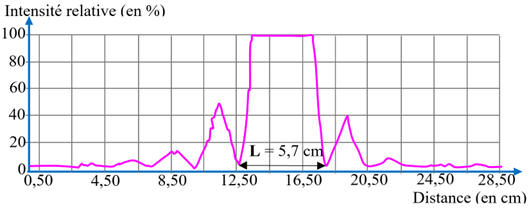
a)-
Décrire la figure observée sur l'écran et
identifier le phénomène correspondant.
b)-
Retenir l'une des relations suivantes
grâce à une analyse dimensionnelle.
- 
; 
;
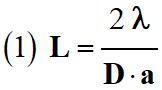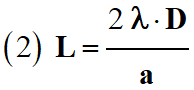(3)
L = 2 λ .
D .
a
c)-
Déterminer la largeur
a
de la fissure.
2)- Correction.
a)-
Le phénomène correspondant.
-
On met ici en évidence le
phénomène de diffraction :
-
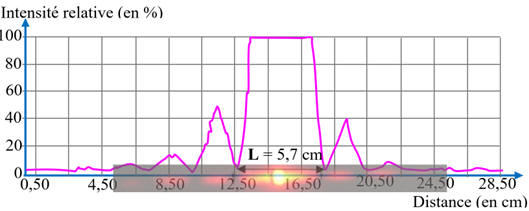
La figure de diffraction est
constituée d’une tache centrale et de taches secondaires situées symétriquement
par rapport à la tache centrale.
-
La tache centrale est très
lumineuse et deux fois plus large que les autres taches.
-
La luminosité diminue très vite
lorsqu’on s’éloigne de la tache centrale de diffraction.
-
La fissure a diffracté la lumière
dans une direction perpendiculaire à celle de la fissure.
-
La diffraction est d’autant plus
marquée que la largeur
a de la fissure est petite.
b)-
Analyse dimensionnelle des relations
suivantes :
-
; ;
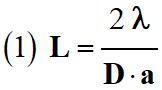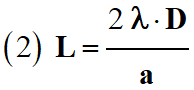(3) L
= 2 λ
. D
. a
►
Une solution :
-
Les notations :
-
La grandeur physique
P (puissance) est représentée
par l’écriture suivante : [P]
-
Son unité est représentée par
l’écriture suivante : (W)
-
On écrit : [P] = (W)
-
Traduction :
-
L’unité de puissance P est le watt W
-
Pour la grandeur physique
L : [L]
= (m)
-
La largeur de la tache L s’exprime
en mètre m.
-
La largeur de la fissure : [a]
= (m)
-
La longueur d’onde : [λ] = (m)
-
Étude de la notation (1) :
-
-
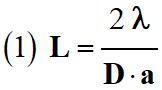
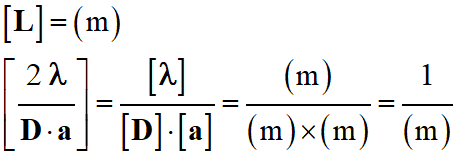
D’après l’analyse dimensionnelle,
on peut affirmer que :
-
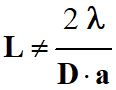La relation (2) est fausse.
-
On peut rejeter cette relation.
-
Étude de la notation (2) :
-
-
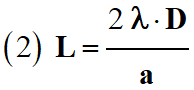
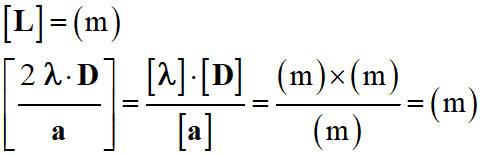
Cette relation peut convenir.
-
Les unités sont cohérentes. On
retient cette relation.
-
Étude de la relation (3) : (3)
L
= 2 λ .
D
. a
-
[L]
= (m)
-
[2
λ .
D . a] = [λ]
. [D].
[a] = (m) × (m) × (m) = (m3)
-
D’après l’analyse dimensionnelle,
on peut affirmer que :
-
(3)
L
≠ 2 λ
. D .
a
La relation (3) est fausse.
-
On peut rejeter cette relation.
►
Remarque : du point de vue
dimensionnel, la relation suivante
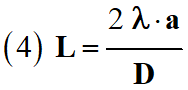peut convenir.
-
L’analyse dimensionnelle est une
analyse nécessaire mais pas suffisante.
-
Elle ne permet pas d’éliminer la
relation (4).
-
On peut l’éliminer en sachant que
la largeur de la tache centrale
L augmente lorsque la largeur
a
de la fissure diminue.
c)-
Déterminer la largeur
a
de la fissure.
►
Figure de diffraction
d’ondes lumineuse monochromatique :
Écart
angulaire θ :
-
L’écart angulaire θ est
l’angle sous lequel est vue la moitié de la tache centrale depuis l’objet
diffractant.
-
C’est le demi-diamètre
angulaire de la tache centrale.
-
Schéma :
-
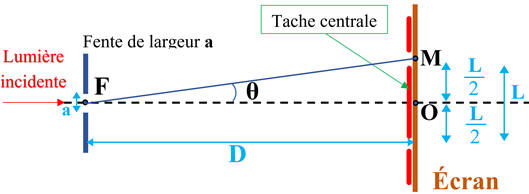
F :
milieu de la fente.
-
O :
milieu de la tache centrale.
-
M :
milieu de la première extinction.
-
L :
largeur de la tache centrale de diffraction.
-
D
>> L :
D est très
grand devant OM.
|
Lorsqu’un faisceau
parallèle de lumière de longueur d’onde λ
traverse une fente de largeur a,
l’écart angulaire θ,
entre le centre de la tache centrale et la première extinction est donné par la
relation suivante :
|
|
|
|
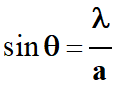
θ
|
Écart angulaire en radian (rad)
|
|
λ
|
Longueur d’onde en mètre (m)
|
|
a
|
Largeur de l’ouverture rectangulaire en mètre (m)
|
-
Si le rapport
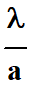est
petit, on peut faire l’approximation suivante :
-
sin
θ
≈ θ
(rad) :
-
la relation s’écrit
alors :
|
|
|
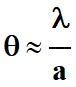
θ
|
Écart angulaire en radian (rad)
|
|
λ
|
Longueur d’onde en mètre (m)
|
|
a
|
Largeur de l’ouverture rectangulaire en mètre (m)
|
-
Cette relation permet
de déterminer expérimentalement la longueur d’onde
λ de la lumière
d’un faisceau connaissant la largeur de la fente.
-
Dans le cas ou
D >> L
(largeur de la
tache centrale), on peut
déterminer la relation donnant la largeur de la tache centrale
L
en fonction de la longueur d’onde λ
et de la largeur a
de la fente.
-
On fait
l’approximation des petits angles.
-
-
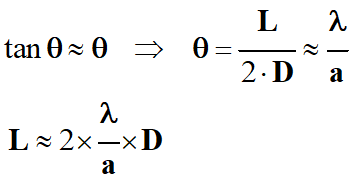
À partir de la relation (2), on
détermine la valeur de la largeur
a
de la fissure :
-
-
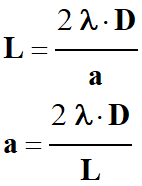
Application numérique :
-
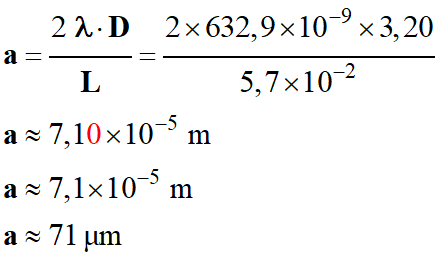
II-
Exercice :
Bulle de savon.
1)- Énoncé.
En observant une bulle de savon, on voit apparaître des
irisations (comme les couleurs de l'arc-en-ciel).
Une bulle de savon est constituée d'un mince film d'eau savonneuse
emprisonnant de l'air.
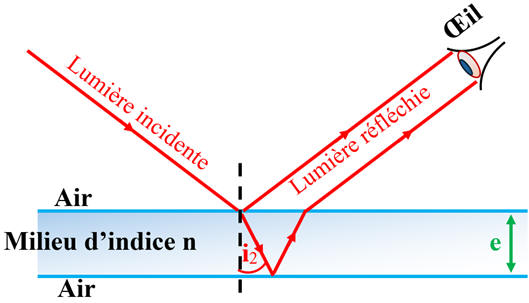
Quand la lumière traverse ce film, il se produit un phénomène d'interférence
entre la lumière réfléchie sur la face supérieure du film et celle réfléchie sur
la face intérieure.
Pour une longueur d'onde dans le vide λ0 et un angle de
réfraction i2 donnés, la différence de chemin optique entre
ces 2 ondes notées δ0, dépend de l'épaisseur e et de
l'indice moyen de réfraction (ou indice optique) n du film d'eau
savonneuse :
-
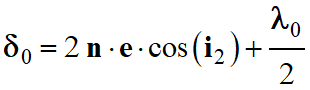
DONNÉES :
-
Indice moyen de réfraction de
l’eau savonneuse : n = 1,35
-
Longueur d’onde dans le vide d’une
radiation rouge : λ0 =
640 nm
a)-
Déterminer si les interférences sont constructives ou destructives
pour une radiation rouge si la valeur de l'épaisseur du film est e = 0,32
μm et si l'angle de réfraction i2 = 42°.
b)-
Proposer une épaisseur de film pour que la bulle apparaisse rouge avec
le même angle de réfraction.
c)-
Expliquer pourquoi il est possible de voir différentes couleurs sur
une bulle de savon.
2)- Correction.
►
Différence de chemin optique. Un exemple :
-
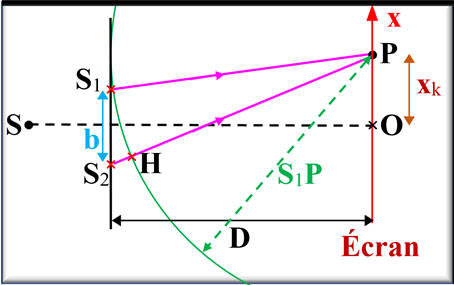
Schéma de la
situation :
-
Les
deux ondes lumineuses de longueur d’onde
λ0
= 632,8 nm émises par les sources secondaires
S1
et S2
se superposent au point
P de l’écran.
-
L’onde
lumineuse, issue de S1,
a parcourue la distance S1P.
-
L’onde
lumineuse, issue de S2,
a parcourue la distance S2P.
-
Les deux ondes ne
parcourent pas la même distance :
-
La différence de
distances :
-
S2H
= S2P
– S1P
-
On
l’appelle aussi la différence de marche :
-
δ
= S2H =
S2P
– S1P
►
Différence de marche
et différence de chemin optique :
-
On
définit le chemin optique
L comme le produit de l’indice
n
de réfraction du milieu de propagation par la distance
e
parcourue par le rayon lumineux dans le milieu :
-
L
= n
. e
-
Le
chemin optique pour l’onde lumineuse issue de
S1
:
-
L1
= n .
S1P
-
Le
chemin optique pour l’onde lumineuse issue de
S2
:
-
L2
= n .
S2P
-
La
différence de chemin optique
ΔL entre les deux ondes est donnée par
la relation :
-
ΔL
= n
. δ =
n
. S2H =
n
. (S2P –
S1P)
►
Interférences
constructives et destructives :
-
Interférences constructives :
-
Si
ΔL
= k
. λ0
avec k
€ ℤ
-
Les
ondes arrivent en phase au point
P.
-
Les interférences sont
constructives.
-
On observe une frange
brillante.
-
Interférences destructives :
-
Si
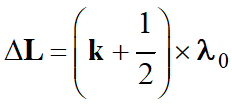avec
k
€ ℤ
-
Les
ondes arrivent en opposition de phase au point
P.
-
Les interférences sont
destructives.
-
On observe une frange
sombre.
►
Remarque :
-
La
longueur d’onde λ d’une radiation lumineuse
dépend du milieu de propagation.
-
Alors
que la période T et de ce fait la fréquence
f
ne dépendent pas du milieu de propagation :
-
Une
onde de longueur d’onde λ0
dans le vide a une longueur d’onde
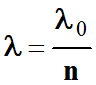dans
un milieu d’indice n.
-
Dans le cas où les
ondes lumineuses se déplacent dans l’air :
-
On fait
intervenir l’indice de réfraction de l’air :
n
= 1,00
-
Dans ce cas, on peut
écrire :
-
ΔL
= n
. δ =
n
. S2H =
n
. (S2P –
S1P)
-
ΔL
= δ
= S2H
= (S2P –
S1P)
►
Dans le cas de la bulle de savon :
-
Schéma simplifié :
-
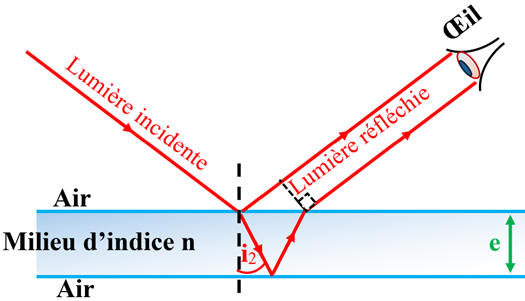
Radiation rouge :
λ0 = 640 nm
-
Épaisseur du film : e = 0,32 μm
-
Angle de réfraction : i2 = 42°.
-
On donne la relation qui permet de calculer la
différence de chemin optique :
-
-
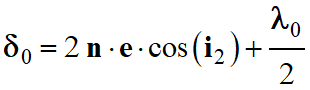
Application numérique :
-
-
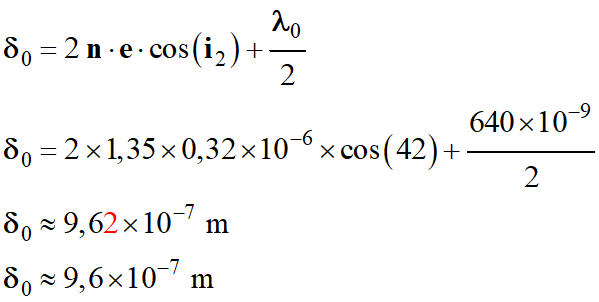
Interférences constructives :
-
Si δ0
= k .
λ0 avec k €
ℤ
-
Interférences destructives :
-
Si
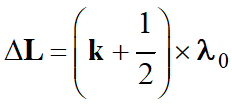avec
k €
ℤ
-
Il faut calculer la valeur du rapport
-
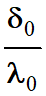
Application numérique :
-
- 
-
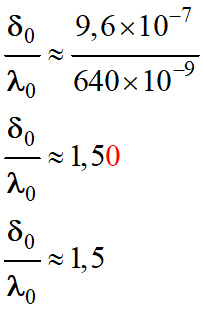
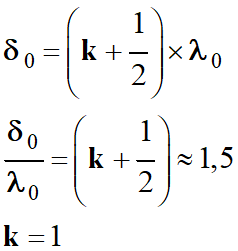
On tire la valeur de
k : k = 1 avec
k €
ℤ
-
Les interférences sont destructives.
b)-
Épaisseur du film pour que la bulle apparaisse rouge
avec le même angle de réfraction.
-
Radiation rouge :
λ0 = 640 nm
-
Épaisseur du film : e = ?
-
Angle de réfraction : i2 = 42°.
-
On donne la relation qui permet de calculer la
différence de chemin optique :
-
-
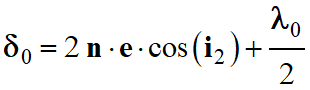
Interférences constructives :
-
Si δ0
= k .
λ0 avec k €
ℤ
-
On prend pour la valeur suivante :
k = 1
-
-
-
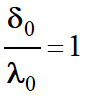
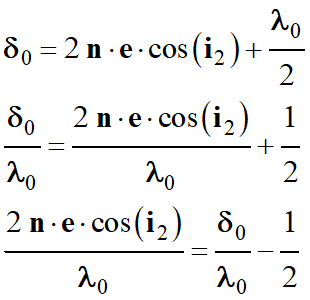
Or :
-
-
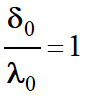
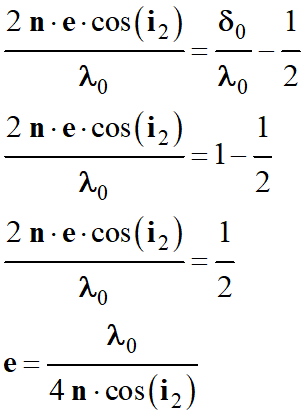
Application numérique :
-
►
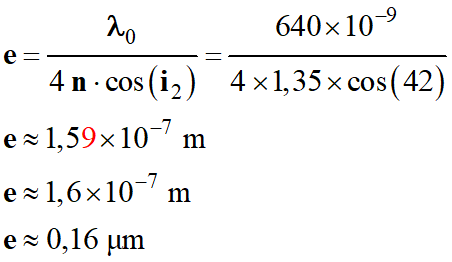
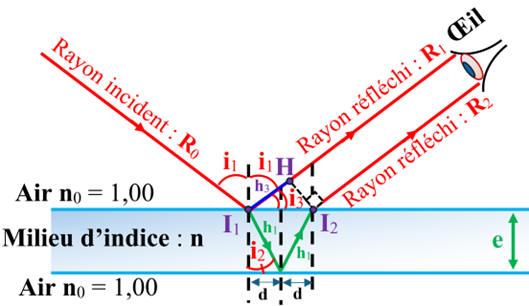
Retour sur la relation :
-
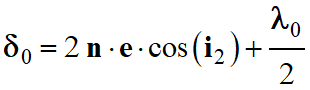
Schéma :
-
Zoom :
-
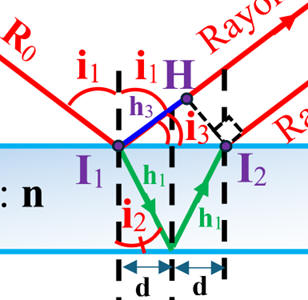
Notations :
-
Le rayon incident
R0 a comme point d’incidence le point
I1 et son angle
d’incidence est i1.
-
Les rayons réfléchis
R1 et R2 :
ce sont des rayons réfléchis consécutifs.
-
Ce sont des rayons parallèles.
-
Les points
I2 et H appartiennent
au même plan d’onde.
-
Les trajets optiques des rayons
R1 et
R2 sont identiques à partir du plan d’onde contenant les
points I2 et
H.
-
L’image se forme à l’infini. L’œil n’a pas besoin
d’accommoder pour la voir.
-
Les rayons
R1 et R2
proviennent du même rayon R0.
-
Différence de marche :
-
δ0 = 2 n . h1
– n0 . h3
-
Or :
-
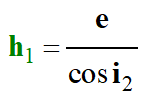
Avec aussi pour la réfraction :
-
n0
. sin i1 =
n . sin i2
-
Étude de la grandeur
h3
-
i3 = π / 2
–
i1
-
-
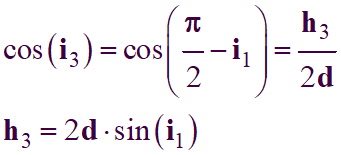
Avec : d =
e . tan (i2)
-
-
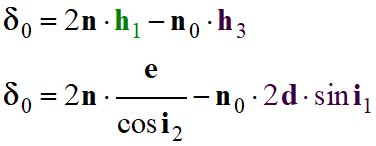
Or n0
. sin i1 =
n . sin i2
-
Et
-
-
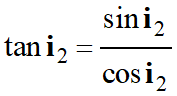
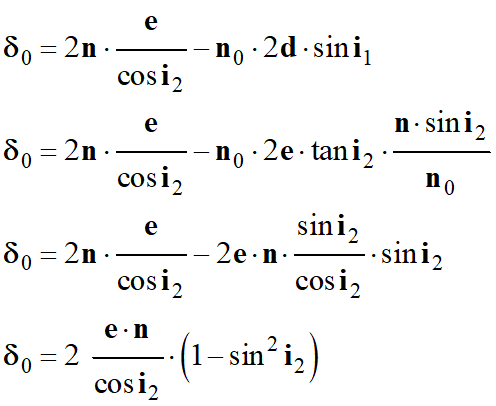
Or sin2
i2 + cos2
i2 = 1
-
-
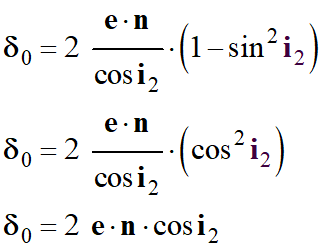
La réflexion d’un rayon lumineux provenant d’un
milieu moins réfringent (ici l’air) sur un milieu plus réfringent (milieu
d’indice n) introduit un déphasage de
π, soit une différence de marche
supplémentaire de
.
-
La différence de marche pour deux rayons
réfléchis consécutifs :
-
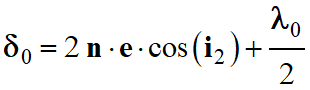
c)-
Différentes couleurs sur une bulle de savon.
https://phymain.unisciel.fr/index.html
(300 expériences commentées et validées)
-
Explications : https://phymain.unisciel.fr/irisations-dune-pellicule-deau-savonneuse/index.html
« Un examen de près montre que les bandes colorées, très espacées au milieu
du cadre, se resserrent au fur et à mesure qu’on se rapproche du bas.
De plus, les couleurs des premières bandes se répètent, avec des degrés de
saturations divers, puis en changeant de teinte.
Toutes les couleurs du spectre visible sont ainsi présentes dans les
irisations.
Ces couleurs ne sont pas dues à une décomposition de la lumière, comme dans
le cas d’un arc-en-ciel.
Elles résultent d’une interférence entre le rayon lumineux qui s’est réfléchi
sur la pellicule de savon et celui qui en est ressorti après avoir fait un ou
plusieurs allers et retours à l’intérieur de cette pellicule.
Selon l’angle d’incidence et l’épaisseur de la couche de savon, certaines
couleurs sont éteintes et d’autres renforcées.
Sous l’effet de la pesanteur, l’eau savonneuse a tendance à s’accumuler vers
le bas : l’épaisseur de la pellicule augmente donc, c’est pourquoi les bandes
irisées se resserrent vers le bas du cadre. »
III- Exercice :
Indice optique .
1)- Énoncé.
L’expérience des fentes d’Young est réalisée dans l’air.
Les deux fentes distantes de a1-2 = 0,30 mm, situées à une
distance D = 2,5 m de l’écran, sont éclairées en lumière monochromatique.
Les deux sources S1 et S2 émettent en
phase.
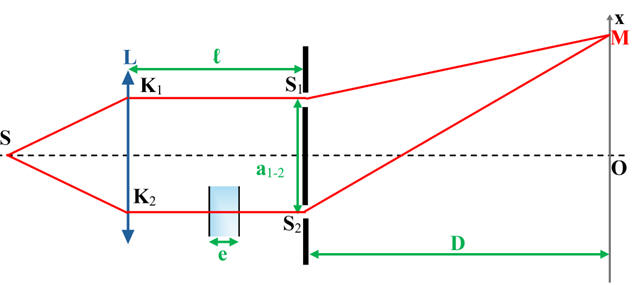
DOC. Schéma du dispositif
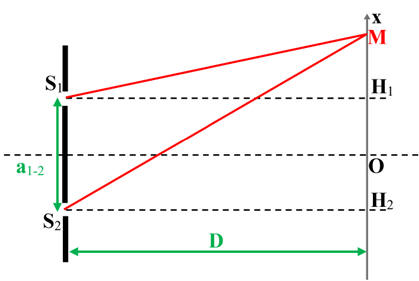
La distance S2M est notée d2 et la
distance S1M est notée d1.
Dans les conditions de l’expérience, D >> a1-2, D
>> x.
DONNÉES :
-
Indices optiques (ou indices de
réfraction) de milieux matériels :
-
nair
= 1,0 ; neau = 1,3 ;
nverre = 1,5 ;
npolycarbonate = 1,6.
DOC. 2 Schéma du dispositif avec une lame d’épaisseur e.
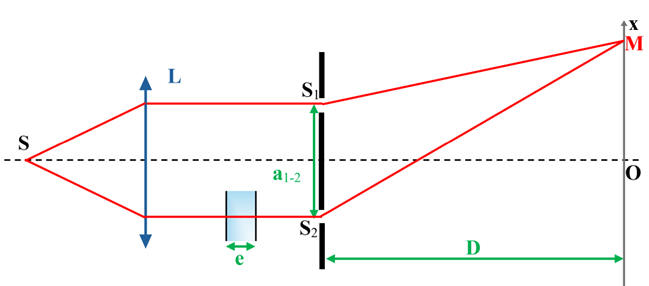
Lorsqu’une lame d’épaisseur e = 0,010 mm d’indice ne
est positionnée devant l’une des fentes, la figure d’interférences se déplace
alors sur l’écran de 4,0 cm du côté de la lame.
Questions
1.
En utilisant le théorème de Pythagore dans des triangles rectangles
convenablement choisis sur le DOC1 ., démontrer que : d22
– d12 = 2x . a1-2.
2.
En utilisant la relation précédente, une identité remarquable et
l’approximation donnée dans le DOC. 1, établir l’expression de la différence de
chemin optique δ0 en fonction de a1-2, x,
D et nair.
3.
Donner l’expression de la différence de chemin optique en M en
présence de la lame d’épaisseur e.
4.
Exprimer et calculer l’indice optique ne et
identifier la nature de la lame.
2)- Correction.
1.
Relation : d22 – d12
= 2 x . a1-2.
-
Choix des triangles rectangles :
►
Le rectangle 1 :
S1H1M
-
DOC1 : avec les notations
-
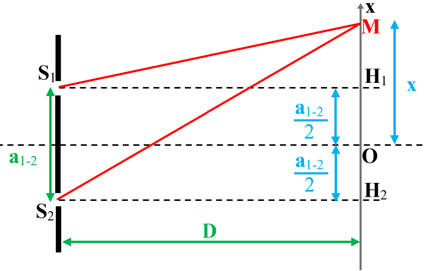
S1H1
= S1H1 ;
-
-
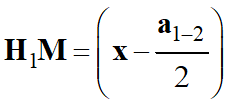
S1M
= d1
-
Théorème de Pythagore dans le
triangle rectangle :
-
►
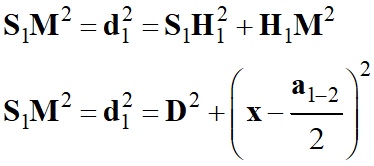
Le rectangle 2 :
S2H2M
-
Théorème de Pythagore dans le
triangle rectangle :
-
►
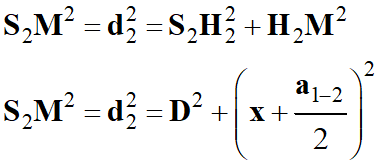
Détermination de l’expression
suivante : d22 – d12 =
-
-
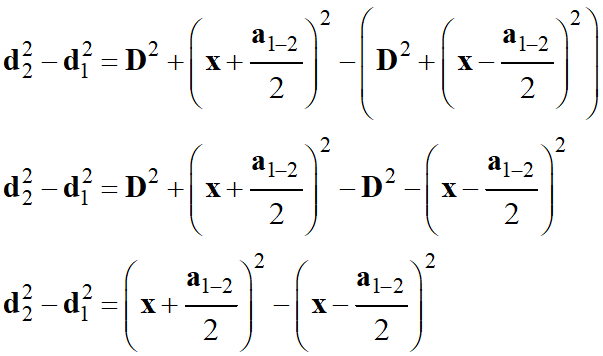
On utilise l’identité remarquable
suivante : a2 –
b2 = (a +
b) . (a – b)
-
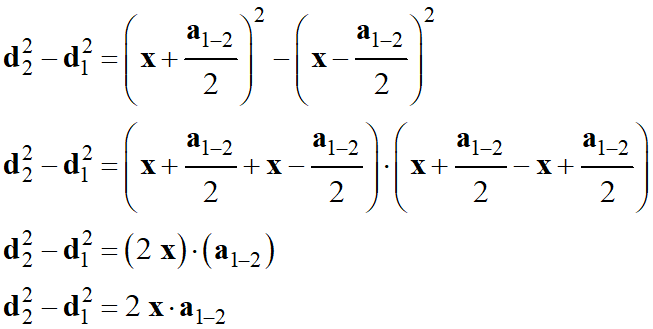
2.
Expression de la différence de chemin optique δ0 en
fonction de a1-2, x, D et
nair.
-
La différence de chemin optique :
-
δ0
= nair . (d2 – d1)
-
La relation de départ : d22
– d12 = 2 x . a1-2.
-
Identité remarquable :
a2 – b2
= (a +
b) . (a –
b)
-
d22
– d12 = (d2 + d1)
. (d2 – d1)
-
Approximation donnée :
D >> a1-2,
D >>
x
-
Or :
-
-
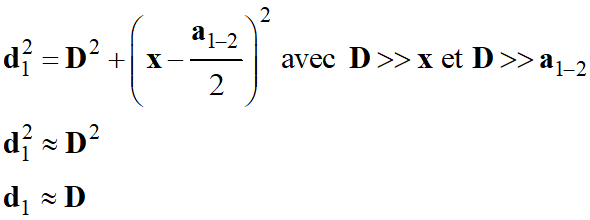
De même :
-
-
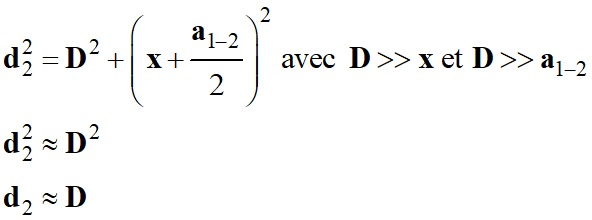
En conséquence : (d2
+ d1) ≈ 2
D
-
d22
– d12 = (d2 + d1)
. (d2 – d1)
-
d22
– d12 ≈ 2 D
. (d2 – d1)
-
En enfin :
-
2 x . a1-2
≈ 2 D . (d2 – d1)
-
-
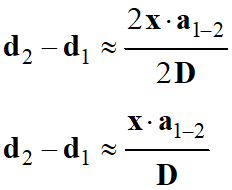
On peut donner l’expression de la
différence de chemin optique :
-
δ0
= nair . (d2 – d1)
-
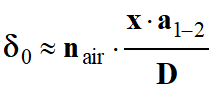
3.
Expression de la différence de chemin optique en M en présence
de la lame d’épaisseur e.
-
Schéma :
-
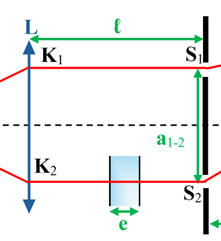
Avant, les fentes :
-
le rayon
K1S1
parcourt la distance ℓ dans l’air d’indice nair.
-
le rayon
K2S2
parcourt la distance ℓ – e dans l’air d’indice nair
et la distance e dans la lame d’indice ne.
-
La différence de chemin optique
pour cette partie du trajet :
-
δ’0
= nair . (ℓ – e)
+ ne .e – nair .ℓ
-
δ’0
= e . (ne – nair)
-
Après les fentes, la différence de
chemin optique n’a pas changé :
-
-
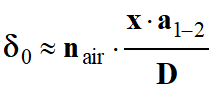
La différence totale de chemin
optique est donnée par la relation suivante :
-
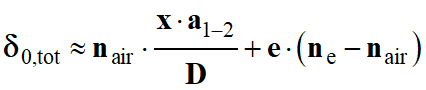
4.
Expression et calcul l’indice optique ne et la
nature de la lame.
-
Lorsqu’une lame d’épaisseur e
= 0,010 mm d’indice ne est positionnée devant la des fente du
bas, la figure d’interférences se déplace alors sur l’écran de 4,0 cm vers le
bas.
-
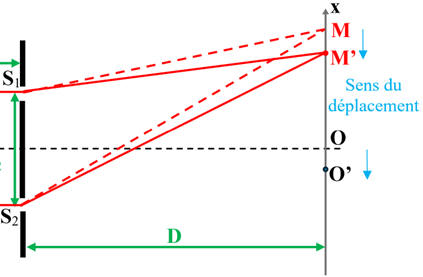
La frange brillante est
positionnée au point O lorsque la différence de chemin optique est nulle.
-
Lorsque l’on place la lame
d’épaisseur e , la frange brillante se trouve au point O’ situé
4,0 cm plus bas.
-
x
(O’) = – 4,0 cm
-
-
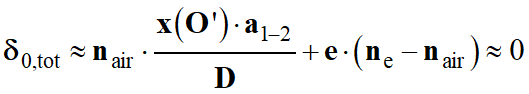
Il faut isoler la grandeur ne.
-
-
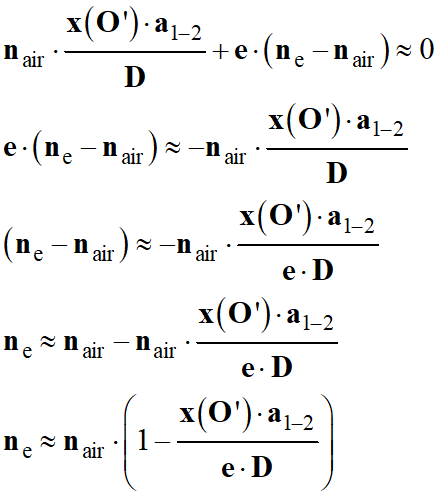
Application numérique :
-
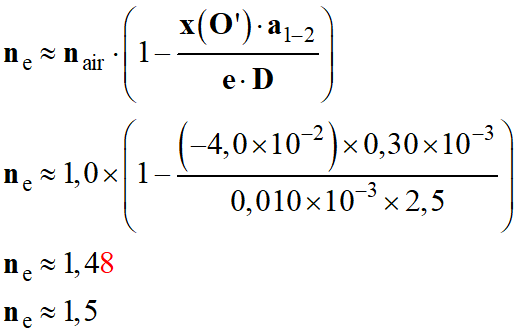
DONNÉES :
-
Indices optiques (ou indices de
réfraction) de milieux matériels :
-
nair
= 1,0 ; neau = 1,3 ;
nverre
= 1,5 ; npolycarbonate
= 1,6.
-
La lame est en verre.
