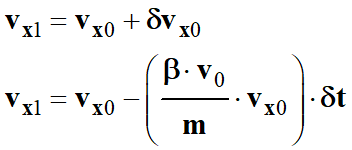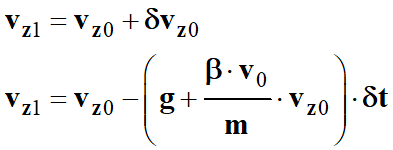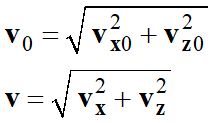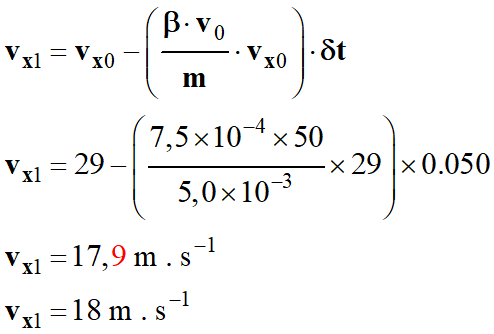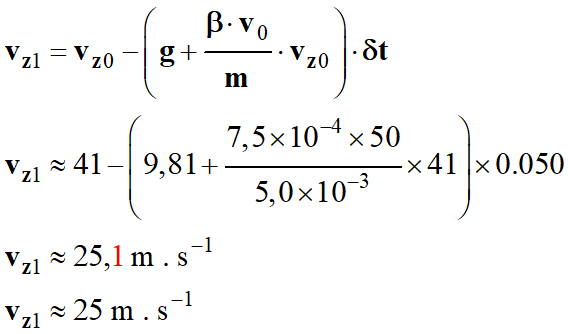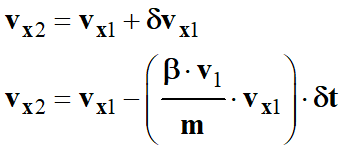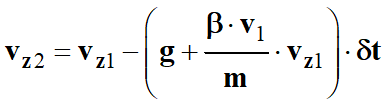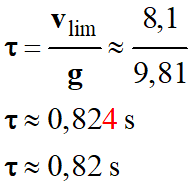Chap N° 12 Exercices 2024 : Mouvement dans un champ uniforme
|
|
I-
Exercice :
Détermination du quotient
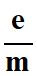 pour l’électron.
pour l’électron.
1)- Énoncé.
Lors de la découverte de l’électron en 1897, le physicien
anglais Joseph John Thomson (1856-1940) utilisa un tube à vide
dans lequel des électrons étaient accélérés à l’aide d’un champ électrique, puis
déviés en passant entre deux plaques métalliques de charges opposées.
Cette expérience a permis la détermination du quotient
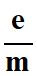 entre la
charge et la masse de cette nouvelle particule.
entre la
charge et la masse de cette nouvelle particule.
DOCUMENT : Expérience de Thomson
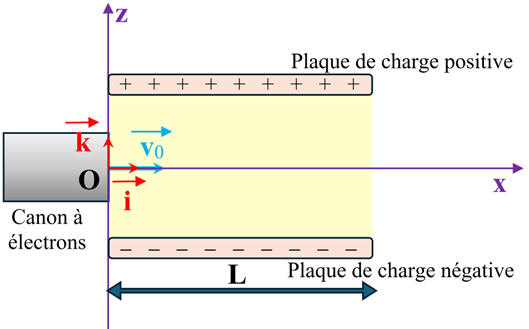
Le montage ci-dessus reprend le principe de l'expérience de Thomson.
Les électrons sortent du canon à électron avec vecteur vitesse horizontal
 , puis se déplace à travers un vide
poussé dans la zone de champ électrique uniforme créée par les 2 plaques
chargées.
, puis se déplace à travers un vide
poussé dans la zone de champ électrique uniforme créée par les 2 plaques
chargées.
La déviation verticale h du faisceau d'électrons lors de la traversée
des plaques sur une longueur L est ensuite mesurée.
DONNÉES :
-
Dans le référentiel terrestre supposé galiléen la
valeur de la vitesse des électrons à la sortie du canon à électrons est :
-
v0
= 2,27 × 107 m . s–1
-
Avec une incertitude-type : u
(v0) = 2 × 105 m . s–1
-
La norme du champ électrique entre
les 2 plaques est :
-
E
= 15,0 kV. m–1
-
Avec une incertitude-type : u
(E) = 0,1 kV. m–1
-
La longueur des plaques est :
-
L
= 8,50 cm
-
Avec une incertitude-type : u
(L) = 0,05 cm
-
On considère que la norme du poids
des électrons est négligeable devant celle de la force électrique
 .
.
-
À la sortie des plaques, en
x =
L, la déviation verticale du
faisceau de l'électrons par rapport à l'axe (Ox)
a une valeur h = 1,85 cm avec une
incertitude-type u (h) = 0,05 cm.
-
L’incertitude-type sur le quotient
s'exprime de la manière suivante :
-
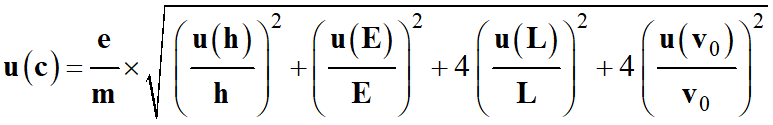
Questions
1.
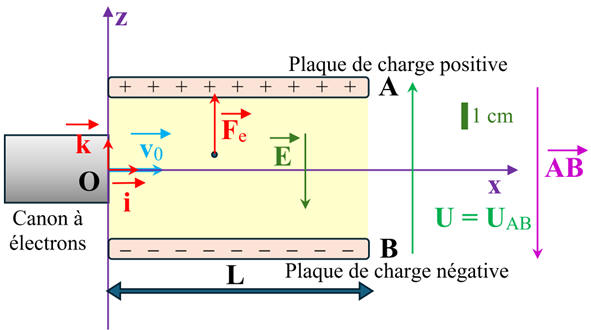
Reproduire le schéma du dispositif et représenter le vecteur champ
électrique
 créé entre des plaques en
utilisant l'échelle suivante : 1,0 cm ↔ 5,0 kV. m-1
créé entre des plaques en
utilisant l'échelle suivante : 1,0 cm ↔ 5,0 kV. m-1
2.
a)-
Donner la relation entre la force électrique
 exercée sur un électron, la charge
élémentaire e et le champ
électrique
exercée sur un électron, la charge
élémentaire e et le champ
électrique
 . En déduire le sens de déviation du faisceau d'électrons.
. En déduire le sens de déviation du faisceau d'électrons.
b)-
Représenter la force électrique
 sur
le schéma en utilisant l'échelle suivante :
sur
le schéma en utilisant l'échelle suivante :
1,0 cm ↔ 1,0 × 10–15
N
3.
En appliquant la deuxième loi de Newton, montrer que les coordonnées
du vecteur accélération de l'électron lors de son mouvement entre les plaques
sont : ax (t) = 0 et
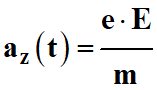 .
.
4.
Établir les équations horaires x (t) et z (t)
du mouvement de l'électron.
5.
Montrer l'équation la trajectoire décrite par les électrons entre les
plaques est :
- 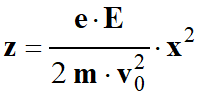
6.
Exprimer le quotient
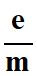 en fonction E, h, L et v0. Calculer la
valeur de ce quotient et de l'incertitude-type associée.
en fonction E, h, L et v0. Calculer la
valeur de ce quotient et de l'incertitude-type associée.

2)- Correction.
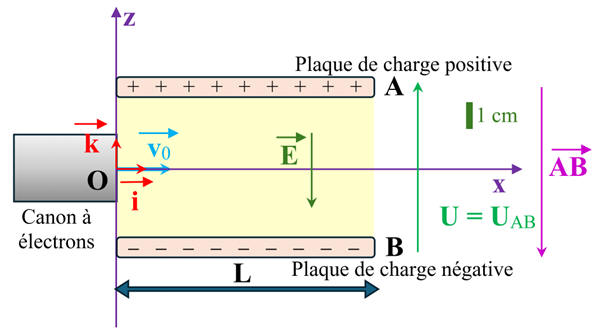
1.
Schéma du dispositif
-
Le vecteur champ électrique
 créé
entre des plaques :
créé
entre des plaques :
-
C’est un champ électrique
uniforme. (Le
condensateur plan)
-
Caractéristiques du champ
électrique
 entre
les plaques :
entre
les plaques :
|

|
|
Direction
|
Perpendiculaire
aux plaques
|
|
Sens
|
De la plaque
chargée positivement
vers la plaque chargée négativement
(sens des
potentiels décroissants)
|
|
Valeur
|
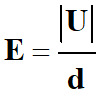 ; E ↑ si
|U| ↑ et d
↓ ; E ↑ si
|U| ↑ et d
↓
|
-
Relation :
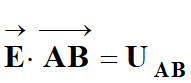
-
Valeur du champ :
|
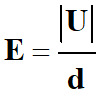
|
|
E
|
Valeur du champ
électrique ( V . m–1)
|
|
U
|
Valeur de la
tension UAB (V)
|
|
d
|
Distance entre
les armatures (m)
|
-
La norme du champ
électrique entre les 2 plaques est :
-
E
= 15,0 kV. m–1
-
Échelle : 1,0 cm ↔ 5,0 kV. m-1
-
Longueur du
représentant du vecteur champ électrique :
-
ℓE
≈ 3,0 cm
2.
a)-
Relation entre la force
électrique
 exercée
sur un électron, la charge élémentaire
e
et le champ électrique
exercée
sur un électron, la charge élémentaire
e
et le champ électrique
 .
.
-
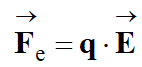
-
Dans le cas de
l’électron :
-
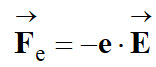
-
La force électrique
 et le champ électrique
et le champ électrique
 ont même direction , mais des sens opposés.
ont même direction , mais des sens opposés.
-
La force électrique
 a même direction et sens que le vecteur
unitaire
a même direction et sens que le vecteur
unitaire
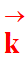 .
.
-
(direction :
perpendiculaire aux plaques et sens : orienté de bas en haut)
-
Sens de déviation du
faisceau d'électrons :
-
L’électron est dévié
vers le haut, vers la plaque chargée positivement.
b)-
Force électrique
 :
:
-
Valeur de la force
Fe :
-
Fe =
e .
E
-
Fe =
1,602
× 10–19
× 15,0 × 103
-
Fe ≈
2,4 ×
10–15
N
-
Échelle : 1,0 cm ↔ 1,0
× 10–15
N
-
Longueur du
représentant du vecteur force :
-
ℓFe
≈ 2,4 cm
3.
Deuxième loi de Newton,
-
Données :
-
Masse :
me
= 9,110 × 10–31 kg ;
-
Charge :
q = – e = – 1,602 × 10–19 C
-
E
= 15,0 kV. m–1
-
g
= 9,81 N . kg–1
-
Système étudié :
l’électron :
-
Référentiel :
Terrestre supposé galiléen
-
Repère d’espace :
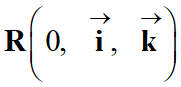
-
Bilan des forces :
inventaire des forces extérieures exercées sur l’électron.
-
Son poids
 .
.
-
La force
électrostatique : 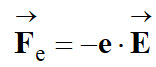
-
L’électron se déplace
dans le vide, il n’y a pas d’interaction avec l’air.
-
Comparaison de
Fe
et P.
-
Fe ≈
2,4 ×
10–15
N
-
P = m . g
≈ 9,1 × 10–31
× 9,81
-
P
≈ 8,9 × 10–30
N
-
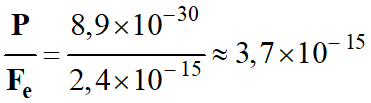
-
En conséquence,
P <<
Fe,
on peut négliger les effets du poids devant celui de la force électrostatique
Fe.
-
Position et vitesse de
l’électron au temps t
= 0 s
-
Coordonnées des
différentes forces et vecteurs dans le repère choisi :
-
Application de la
deuxième loi de Newton :
-
Dans le cas présent :
-
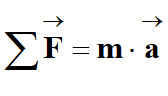
-
D’où :
-

-
Le vecteur
accélération
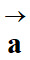 a
même direction mais un sens opposé au vecteur champ électrique
a
même direction mais un sens opposé au vecteur champ électrique
 .
.
-
Coordonnées du vecteur
accélération
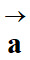 de l'électron :
de l'électron :
-
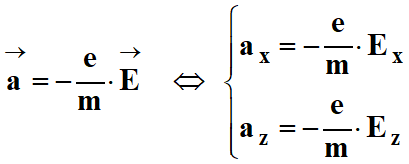
-
On tire les
coordonnées du vecteur accélération :
-
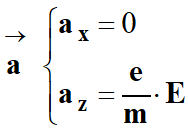
-
Ceci est bien en
accord avec les relations données dans l’énoncé.
-
ax
(t) = 0
-
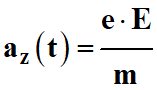 .
.
4.
Équations horaires
x (t)
et z (t)
du mouvement de l'électron.
-
Par recherche des
primitives, on retrouve les coordonnées du vecteur vitesse et du vecteur
position :
-
Le vecteur
accélération
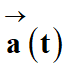 est
la dérivée par rapport au temps du vecteur vitesse
est
la dérivée par rapport au temps du vecteur vitesse
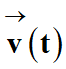 .
.
-
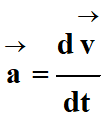
-
La détermination du
vecteur vitesse nécessite de rechercher la primitive par rapport au temps de
chaque coordonnée du vecteur accélération en tenant compte des conditions
initiales.
-
On cherche les
primitives des équations précédentes.
-
Il apparaît des
constantes qui sont liées aux conditions initiales.
-
Les constantes
d’intégration apparues dans les primitives sont liées aux conditions initiales :
-
c’est-à-dire les
coordonnées du vecteur vitesse
 à
l’instant initial.
à
l’instant initial.
|
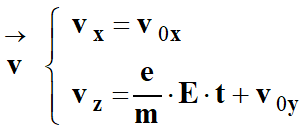
|
D’après
les
conditions
initiales
|
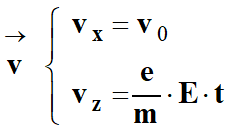
|
-
Le vecteur vitesse
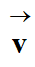 est
la dérivée par rapport au temps du vecteur position
est
la dérivée par rapport au temps du vecteur position
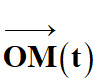
-
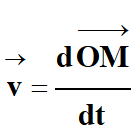 notation simplifiée
notation simplifiée
-
On opère de la même
façon :
|
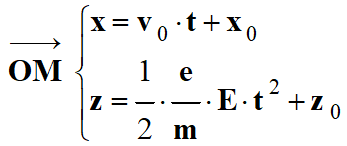
|
D’après les
conditions
initiales
|
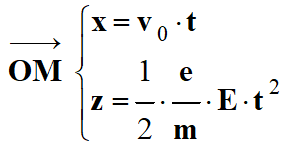
|
5.
Équation de la trajectoire
décrite par les électrons entre les plaques :
-
On élimine le temps
t entre
x
et z
pour exprimer
z
= f (x).
-
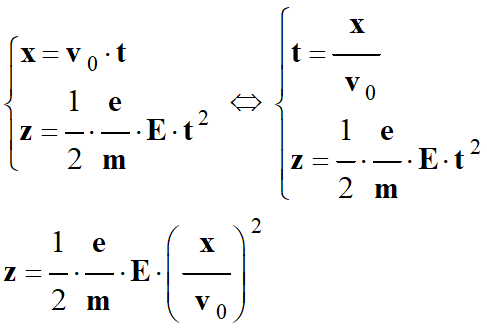
-
En ordonnant, on
obtient la relation suivante :
-
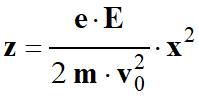
6.
Expression du quotient
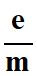 en
fonction
E,
h,
L et
v0.
en
fonction
E,
h,
L et
v0.
-
Données :
-
À la sortie des
plaques, en x
= L, la
déviation verticale du faisceau de l'électrons par rapport à l'axe (Ox)
a une valeur h
= 1,85 cm avec une incertitude-type u
(h) = 0,05
cm.
-
La longueur des
plaques est : L
= 8,50 cm avec une incertitude-type : u
(L) = 0,05
cm
-
Expression du quotient
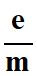 : avec
x =
L et
z =
h
: avec
x =
L et
z =
h
-
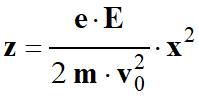
-
On réorganise la
relation précédente :
-
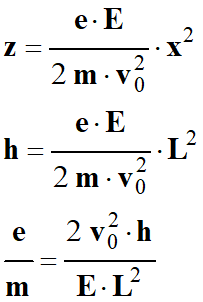
-
Application
numérique :
-
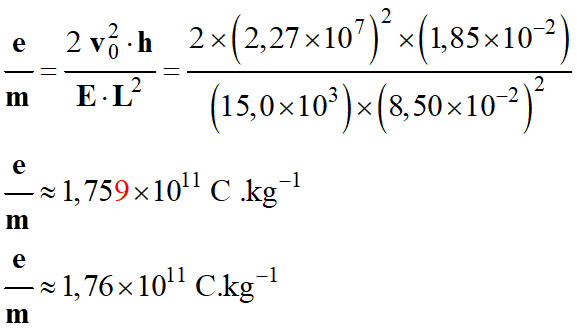
-
Incertitude-type
associée :
-
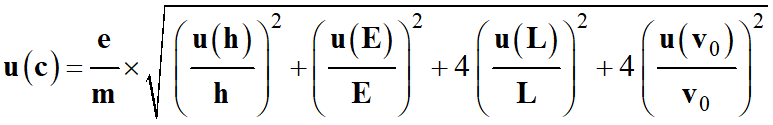
-
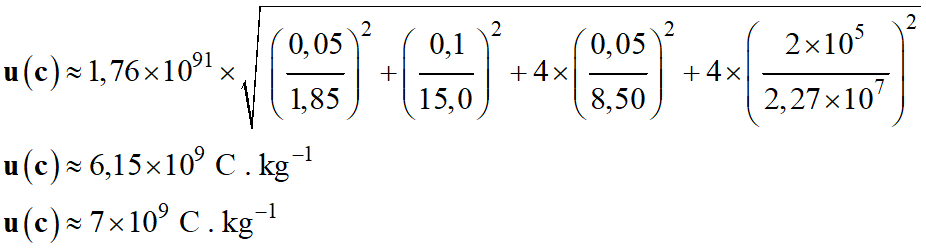
-
On arrondit à l’unité
supérieure.
-
L'incertitude-type u (c)
est arrondie généralement par excès en ne conservant qu’un seul chiffre
significatif.
-
On arrondit à la
valeur supérieure pour ne pas minorer l’incertitude-type.
-
On peut
écrire : u (c)
= 0,07 × 1011 C . kg–1
-
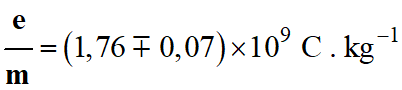
-
Autre écriture :
-
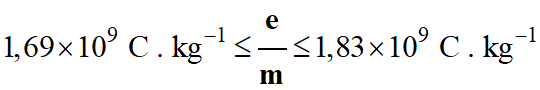
-
Comparaison avec la
valeur de référence :
-
Charge
élémentaire e = 1,602 × 10–19
C
-
Masse
de l’électron : m = 9,110 × 10–31
kg
-
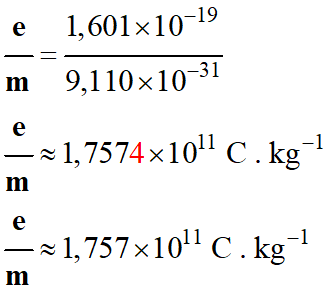
-
La valeur trouvée est
en accord avec la valeur de référence.

II-
Exercice :
Mouvement d’un volant de badminton.
1)- Énoncé.
Au badminton, les joueurs envoient à l'aide d’une raquette un
volant de masse m = 5,0 g qui possède des propriétés aérodynamiques
particulières.
Sa vitesse peut dépasser la valeur de 400 km . h–1
et sa trajectoire est très différente de celle des balles utilisées dans
d'autres sports comme le tennis.
Le mouvement du centre de masse du volant est étudié dans le référentiel
terrestre supposé galiléen, lié au
repère d'espace cartésien
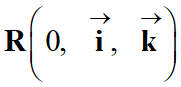 .
.
Dans la situation considérée, le volant quitte la raquette à la date t
= 0 s avec un vecteur vitesse
 incliné d'un angle α = 55° avec
l'horizontale et de norme v0 = 50 m . s–1.
incliné d'un angle α = 55° avec
l'horizontale et de norme v0 = 50 m . s–1.
Le langage de programmation Python permet de concevoir un programme qui
détermine, par itérations successives, la trajectoire du centre de masse du
volant et l'évolution au cours du temps de son énergie mécanique.
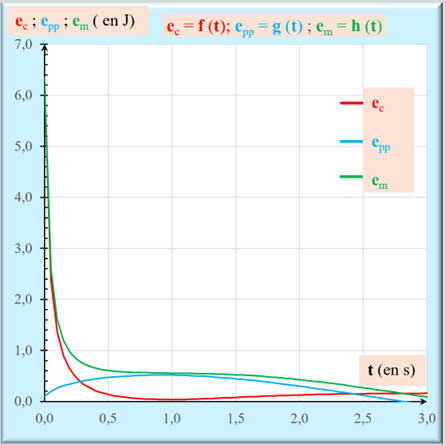
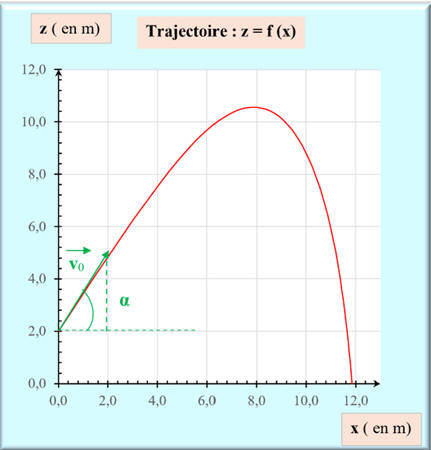
DOC. 1 : Trajectoire du
centre de masse et évolution temporelle
des différentes formes d'énergie du volant de badminton
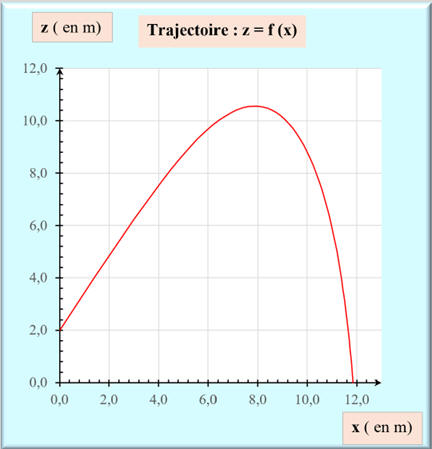
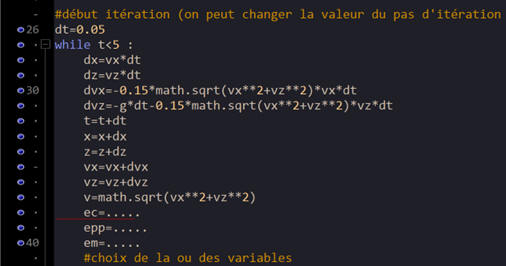
DOC. 2 : Extrait du code source Phyton :
DONNÉES : Caractéristique de la force de traînée
-
Les plumes du volant créent une
traînée modélisée par une force
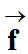 qui s'oppose au mouvement du volant dans l'air.
qui s'oppose au mouvement du volant dans l'air.
-
On a
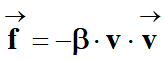 avec β = 7,5 × 10–4
SI et v la valeur de la vitesse du volant.
avec β = 7,5 × 10–4
SI et v la valeur de la vitesse du volant.
-
Intensité de la pesanteur :
g = 9,81 N . kg–1
Questions
1.
À l’aide du DOC. 1 , justifier que le volant n’effectue pas une chute
libre.
2.
Comparer les normes du poids du volant et de la force de traînée à la
date t = 0. Commenter.
3.
En utilisant la deuxième loi de Newton et en sachant que l'axe
vertical est orienté vers le haut, exprimer le vecteur accélération du centre de
masse du volant.
4.
Établir les équations ci-dessous en précisant les expressions des
constantes A, B et C en fonction de k, m et
g.
-
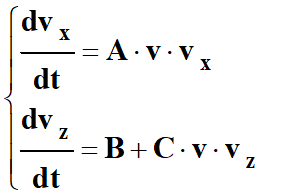
5.
Déterminer les valeurs numériques des constantes A, B et
C. Vérifier leur cohérence avec les lignes 30 et 31 de l'extrait du code
Python présenté dans le DOC. 2.
6.
Compléter les lignes 38 à 40 de l'extrait du code source Python de
manière à déterminer l'évolution des différentes formes d'énergie du volant de
badminton. Commenter cette évolution.

2)- Correction.
1.
Caractéristiques du mouvement du volant.
-
Graphe
z =
f (x)
-
Le système : le volant S =
{M}
-
Conditions initiales :
-
Vecteur vitesse
 incliné d'un angle α = 55° avec l'horizontale et de norme v0=
50 m . s–1.
incliné d'un angle α = 55° avec l'horizontale et de norme v0=
50 m . s–1.
-
Position et vitesse du volant au
temps t = 0 s
-
Bilan des forces :
-
Le poids :

-
La force de traînée :
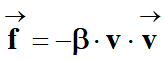
-
Étude de la trajectoire
z =
f (x) :
-
Au départ, le mouvement est
quasiment rectiligne, puis le mouvement devient curviligne.
-
La trajectoire obtenue n’est pas
parabolique.
-
Le volant de badminton n’est pas
en chute libre.
-
Le volant est soumis à la force de
traînée et à son poids.
-
Comme au départ, la vitesse du
volant est grande, la force de traînée est prépondérante devant le poids du
volant.
-
Un objet en chute libre n’est
soumis qu’à son poids.
-
Ce qui n’est pas le cas du volant
de badminton.
2.
Normes du poids du volant et de la force de traînée à la
date t = 0.
-
Le vecteur poids :

-
Norme du poids
-
P
= m .
g
-
P
= 5,0 × 10–3 × 9,81
-
P
≈ 4,90 × 10–2
N
-
P
≈ 4,9 × 10–2
N
-
Le vecteur force de traînée :
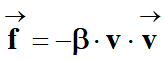
-
Norme de la force de traînée :
-
F
= β .
v2
-
F
= 7,5 × 10–4 × (50)2
-
F
≈ 1,87 N
-
F
≈ 1,9 N
-
Comparaison des normes :
-
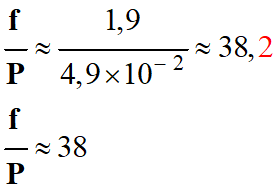
-
La norme de la force de traînée
exercée par l’air sur le volant de badminton est environ 40 plus grande que
celle du poids.
-
L’action de l’air ne peut pas être
négligée.
-
La force de traînée influence
grandement le mouvement du volant ceci tant que sa vitesse est importante.
3.
Vecteur accélération du centre de masse du volant.
-
Le système : le volant
S = {M}

-
Conditions initiales :
-
Vecteur vitesse
initiale
 incliné d'un angle α = 55° avec l'horizontale et de norme v0=
50 m . s–1.
incliné d'un angle α = 55° avec l'horizontale et de norme v0=
50 m . s–1.
-
Schéma à l’instant
t :
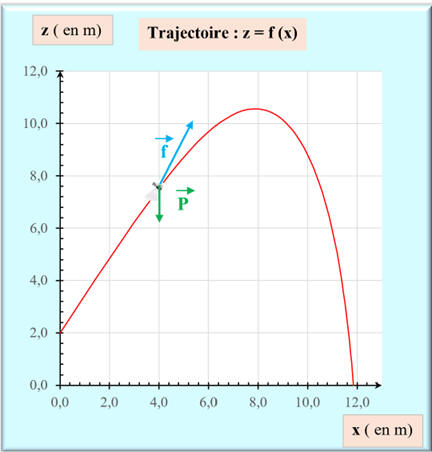
-
Position et vitesse du volant au temps t = 0 s
-
Bilan des forces :
-
Le poids :

-
Le vecteur poids a comme direction
la verticale du lieu et il est orienté du haut vers le bas.
-
La force de traînée :
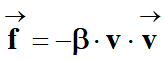
-
Le vecteur force de traînée a même
direction que le vecteur vitesse, mais un sens opposé.
-
Deuxième loi de Newton :
|
Dans un référentiel galiléen, la
somme des vecteurs forces 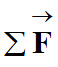
appliquées à un
système S, de masse m et de centre de masse G,
est égal au
produit de sa masse m par le vecteur accélération
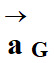
de son centre de
masse.
|
|
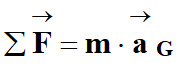
|
Valeur des
forces F en newton (N)
|
|
Valeur de la
masse m en kilogramme (kg)
|
|
Valeur de
l’accélération aG en mètre par
seconde au carré
(m . s–2)
|
-
Référentiel d’étude :
Référentiel terrestre supposé galiléen
-
Repère lié au référentiel d’étude
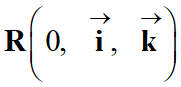 .
.
-
Dans le cas présent :
-
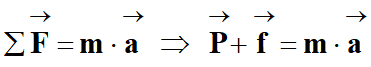
-
Le vecteur accélération :
-
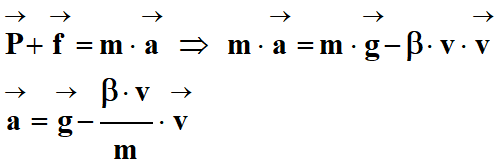
4.
Établissement les équations du
mouvement.
-
Coordonnées des différents
vecteurs :
-
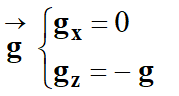
-
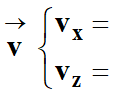
-
On utilise le fait que le vecteur
accélération
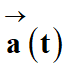 est la dérivée par rapport au temps du vecteur vitesse
est la dérivée par rapport au temps du vecteur vitesse
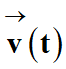 .
.
-
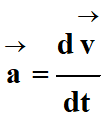
-
Coordonnées du vecteur
accélération dans le repère
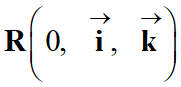
-
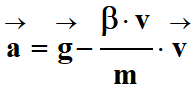
-
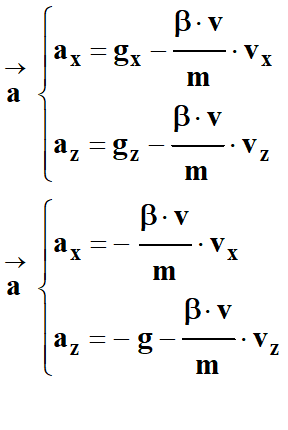
-
Or :
-
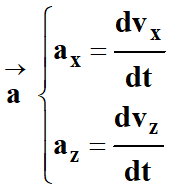 et
et
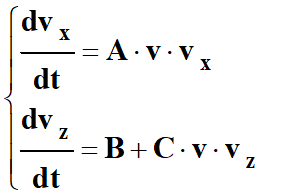
-
Expressions des constantes A,
B et C en fonction de k, m et
g
-
On en déduit les relations
suivantes :
- 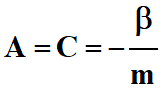 et
B = –
g
et
B = –
g
5.
Valeurs numériques des constantes A, B et
C.
-
Valeurs numériques de A et
C :
-
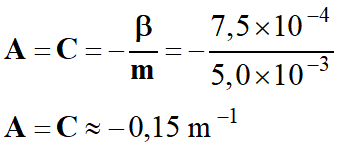
-
B = –
g =
–
9,81
N . kg–1 =
–
9,81
m . s–2
-
Cohérence avec les lignes 30 et 31
de l'extrait du code Python présenté dans le DOC. 2
-
Les lignes 30 et 31 :
-
30
dvx=
– 0,15 * math.sqrt (vx**2+vz**2)*vx*dt
-
31
dvz= – 9,81– 0,15 *math. sqrt (vx**2+vz**2)*vz*dt
-
Programme Python :
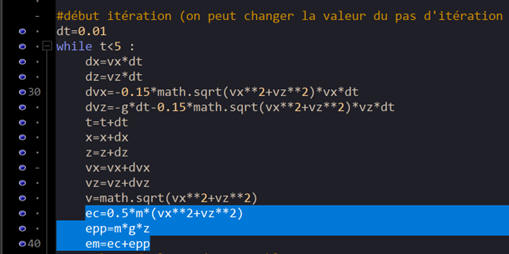
6.
Code source Python :
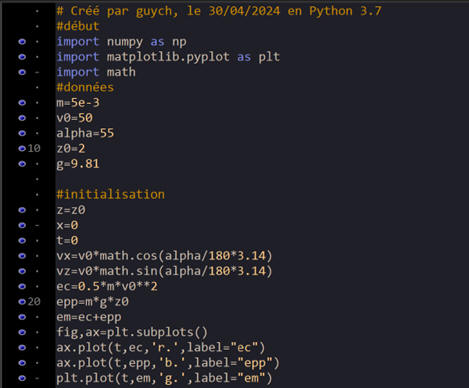
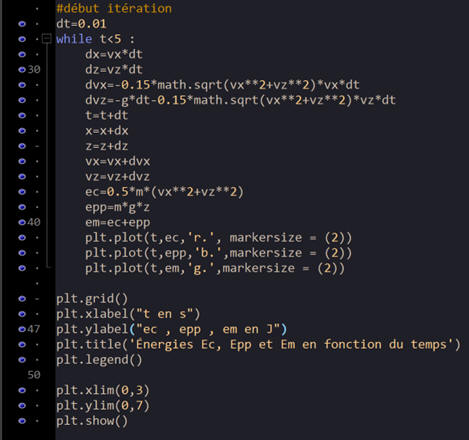
Courbes obtenues avec le Programme Python
-
On
peut décomposer le mouvement du volant de badminton en plusieurs phases
-
Première phase :
-
Le mouvement du volant de
badminton est rectiligne uniformément retardé.
-
La valeur du poids du badminton
est négligeable par rapport à la force de traînée.
-
La valeur de la vitesse diminue
rapidement.
- La direction du mouvement est celle du vecteur vitesse initiale
 .
.
-
Deuxième phase :
-
Le mouvement du volant de
badminton est curviligne décéléré .
-
La valeur du poids du badminton
n’est plus négligeable par rapport à la force de traînée.
-
La valeur de la vitesse diminue,
passe par une valeur minimale (sommet de la trajectoire).
-
vz = 0
et vx ≈ 4,0 m . s-1
-
Troisième phase :
-
Le mouvement du volant de
badminton est curviligne accéléré.
-
La valeur du poids du badminton
n’est pas négligeable par rapport à la force de traînée.
-
La valeur de la vitesse augmente
et tend vers une valeur limite vlim.
-
Quatrième phase :
-
Le mouvement du volant de
badminton est rectiligne uniforme (direction : verticale du lieu).
-
La valeur du poids est égale à la
valeur de la force de traînée : P =
f
-
v =
vlim ≈ 8,1 m . s-1
-
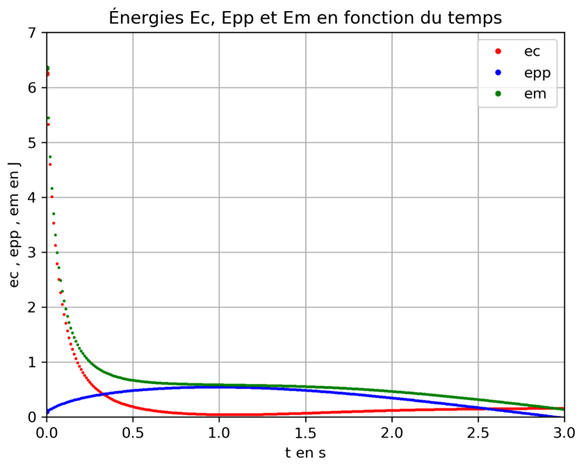
Évolution temporelle
des différentes formes d'énergie du volant de badminton
-
L’énergie cinétique
ec est maximale au départ ;
-
Elle diminue rapidement puis plus
lentement ;
-
Elle passe par une valeur minimale
(sommet de la trajectoire)
-
Puis l’énergie cinétique augmente
et tend vers une valeur limite lorsque la vitesse limite est atteinte.
-
L’énergie potentielle
epp augmente au cours du temps.
-
Elle passe par une valeur maximale
( sommet de la trajectoire)
-
Puis l’énergie potentielle diminue
au cours de la chute.
-
L’énergie mécanique
em diminue
au cours du temps, d'abord rapidement, puis plus lentement, elle ne se conserve pas.

3)- Additif :
Cas de frottements quadratiques.
1-
Équation différentielle
-
Deuxième loi de Newton :
-
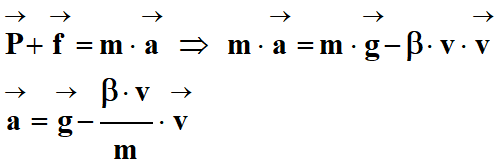
-
On utilise un axe
Oz vertical
ascendant.
2- Coordonnées du vecteur
accélération :
-
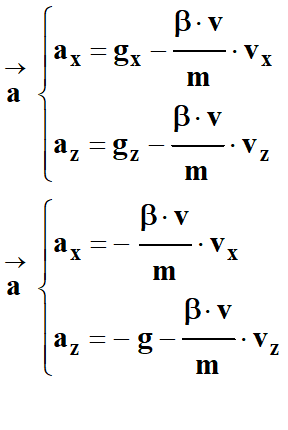
-
Ces équations différentielles ne
sont pas linéaires, nous ne pouvons pas les résoudre facilement.
-
Vitesse limite :
-
Lorsque la vitesse limite est
atteinte, le mouvement du volant a comme direction la verticale du lieu :
-
dans ce cas
vx = 0 et
vz = -
v = - vlim
-
Le mouvement est alors rectiligne
uniforme et le vecteur vitesse limite est vertical et orienté du haut vers le
bas :
-
On peut déterminer l’expression de
la vitesse limite suivant axe Oz :
-
Lorsque :
-
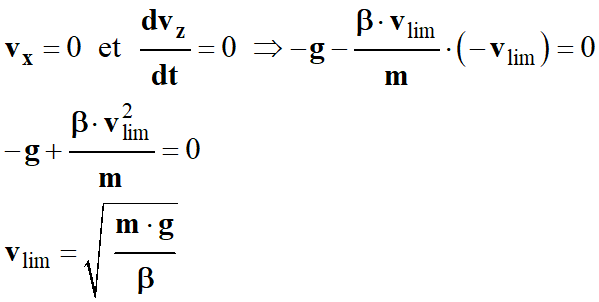
-
Application numérique :
-
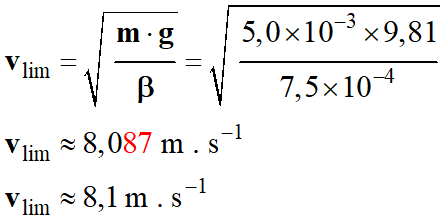
►
Les équations différentielles :
-
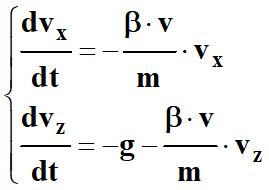
-
Chaque équation différentielle,
complexe à résoudre, va être l’occasion d’utiliser une méthode de résolution
numérique itérative: la méthode d’Euler.
►
Méthode
d’Euler :
Chute verticale dans un fluide
Résolution
d'une équation différentielle non linéaire
Le saut à l'élastique
Chute libre et parachutisme
Chute
verticale d'une bille dans l'huile
-
La méthode d’Euler est une méthode
numérique itérative qui permet d’obtenir une solution approchée d’une équation
différentielle à partir des conditions initiales.
-
On peut alors écrire, en
considérant un intervalle de temps
δt suffisamment petit:
-
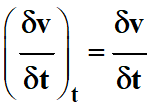
-
On peut alors exprimer la petite
variation de vitesse
δv qui se produit
pendant le petit intervalle de temps
δt grâce à l’équation
différentielle :
-
Les équations différentielles :
-
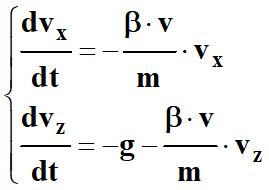
-
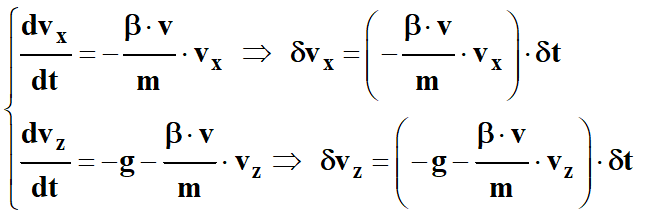 lorsque δt → 0
lorsque δt → 0
3- Mise en œuvre :
-
On part de la condition initiale,
la valeur de v(t=0) = v0;
-
On choisit le pas de calcul, soit
la valeur de δt :
-
On calcule:
-
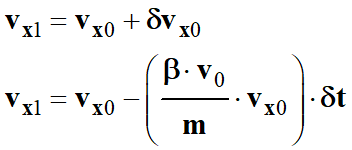
-
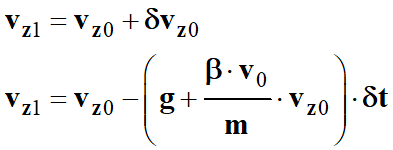
-
Avec :
-
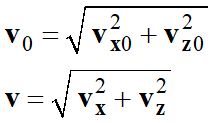
-
On peut utiliser un tableur pour
effectuer les calculs répétitifs.
-
Le choix du pas de calcul δt
doit être judicieux :
-
Il faut prendre un intervalle
suffisamment petit pour que l’approximation soit valable, mais pas trop petit
afin que les calculs ne soient pas trop longs.
-
Utilisation de cette méthode dans
le cas présent :
-
Obtention de la vitesse en fonction du temps :
-
On connaît la vitesse initiale
v0 = 50 m . s-1
avec α = 55 ° et la vitesse
limite vlim ≈ 8,1 m . s-1
-
vx0 =
vo cos
α = 50
× cos 55 => vx0 ≈ 28,7
m . s-1 ≈ 29 m . s-1
-
vz0 =
vo sin
α = 50
× sin 55 => vz0 ≈ 40,9
m . s-1 ≈ 41 m . s-1
-
On peut donc appliquer la méthode
en choisissant un pas δt judicieux.
-
On prendra par exemple
δt =0,050 s.
-
Alors :
-
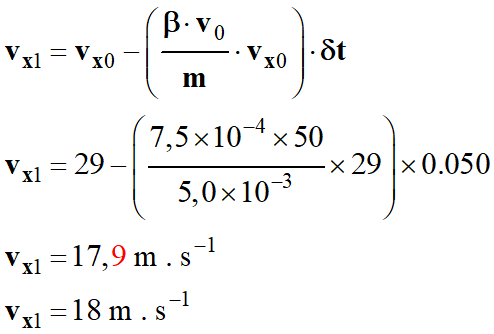
-
On fait
de même pour vz1 :
-
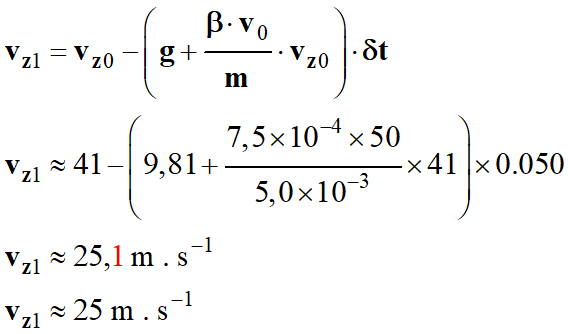
-
Avec :
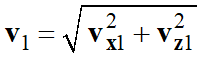
-
À l’aide d’un tableur, on répète
les calculs jusqu’au temps voulu.
-
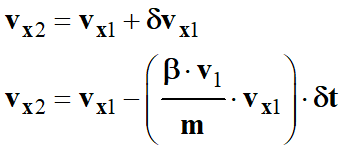 et
et
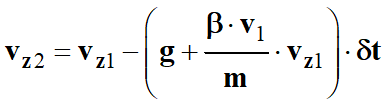
-
On peut ensuite tracer la courbe
vz = f (t),
vx = g (t) et
v = h (t),
-
Ci-dessous, on a tracé les courbes
pour des pas de calculs différents.
-
On remarque qu’il n’y a pas de
différences entre nos trois tests.
-
Qu’en est-il de la position en
fonction du temps?
-
Pour obtenir la courbe de position
en fonction du temps, on part de la donnée de vitesse et on calcule la distance
parcourue par la formule classique v
= d /
t.
-
On utilise cette
formule pour chaque ligne du tableur dans lequel on a exploité la méthode
d’Euler.
-
Pour connaître
x au cours du temps :
-
On utilise :
δx =
vx .
δt et
x =
x +
δx
-
On utilise :
δz =
vz .
δt et
z =
z +
δz
-
Ainsi :
-
x0 = 0
-
x1
= x0
+ δx0 =
x0 +
vx0 .
δt ≈ 0 +
29 ×0.050
-
x1
≈ 1,43 m ≈ 1,4 m
-
Pour la côte :
-
z0 =
2,0 m
-
z1
= z0
+ δz0
= z0 + vz0
. δt ≈ 2,0 + 41 × 0.050
-
z1
≈ 4,04 m ≈ 4,0 m
-
Pour obtenir la trajectoire du
volant de badminton, on trace la courbe
z = f (x).
-
À partir des valeurs de
x,
z,
v, on peut calculer :
-
L’énergie cinétique
EC du volant de badminton
au cours du temps ;
-
L’énergie potentielle de pesanteur
EPP du volant de
badminton au cours du temps ;
-
Et son énergie mécanique
Em.
►
Choix
de
δt :
-
La valeur de la vitesse du volant
de badminton tend vers une valeur limite :
-
vlim ≈
8,1 m . s-1
-
La constante de temps
τ du mouvement du volant de badminton
peut être définie à partir de la vitesse limite :
-
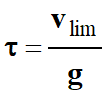
-
Application numérique :
-
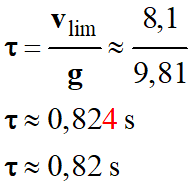
-
Avec des frottements quadratiques
le régime permanent est atteint au bout de 2,5
τ environ.
-
En conséquence au bout de 2,1 s
environ.
-
À ce temps, on peut rajouter une
seconde,
-
Ainsi on étudie de mouvement du
volant de badminton pendant 3,1 secondes environ.
-
Avec un pas de calcul de 50 ms, on
aura une soixantaine de valeurs
-
Avec un pas de calcul de 10 ms, on
aura 310 de valeurs.
-
Avec un pas de calcul de 5 ms, on
aura 620 de valeurs.
4-
Exploitation avec le tableur Excel :
a)-
Fichier Excel :
Badminton_Euler
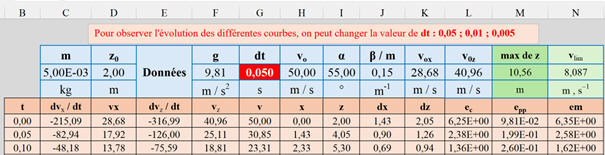
b)-
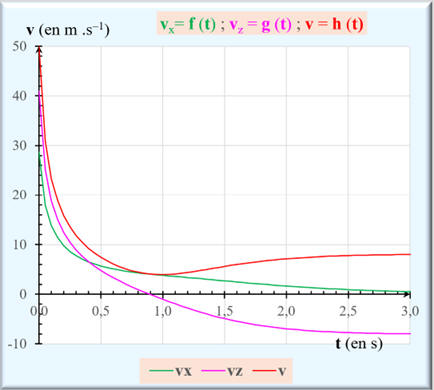
Les différentes courbes :
-
Graphes obtenus avec un pas de 50
ms :
-
Trajectoire du volant de
badminton : z =
f (x) :

-
ec =
f (t) ;
ePP =
g (t) ;
em =
h (t)

-
vx =
f (t) ;
vz =
g (t) ;
v =
h (t)
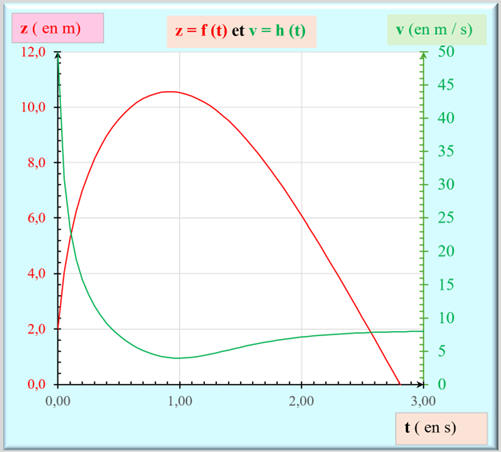
c)-
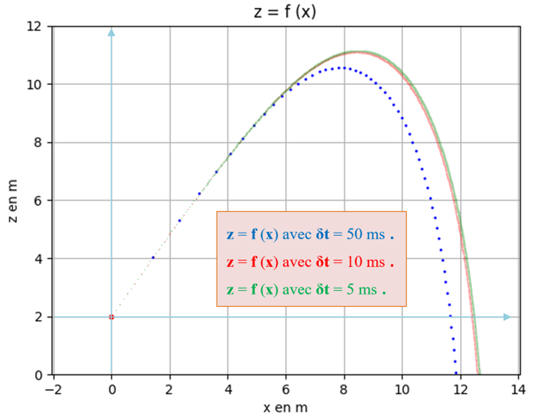
Évolution de la courbe z =
f (x) en fonction du pas dt d’itération.
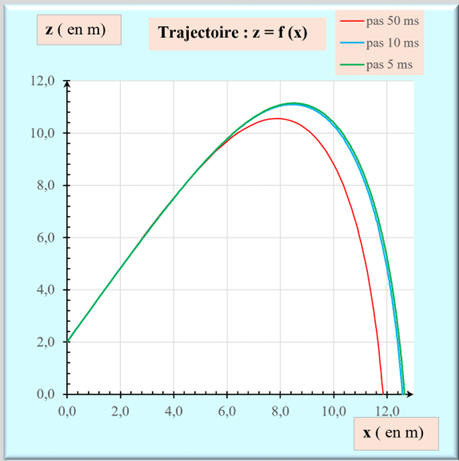
-
Lorsque la valeur du pas du calcul
dt diminue, cela se traduit par une meilleure approximation de la
solution.
-
Ainsi pour dt = 10 ms et
dt = 5 ms, on obtient pratiquement la même trajectoire.
-
La première partie de la
trajectoire est pratiquement la même pour les différents pas de calcul.
-
Ce qui change sensiblement :
-
la flèche (
zmax
≈ 10,56 m ; zmax
≈ 11,09 m ;
zmax
≈ 11,14 m)
-
la portée (
xmax
≈ 11,86 m ; xmax
≈ 12,58 m ; xmax
≈ 12,66 m)
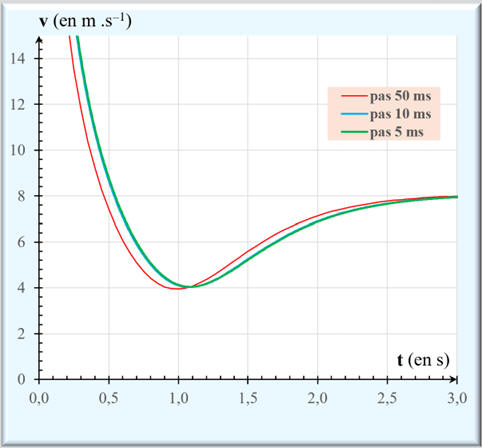
d)-
Évolution de la courbe v =
h (t) en fonction du pas dt d’itération.
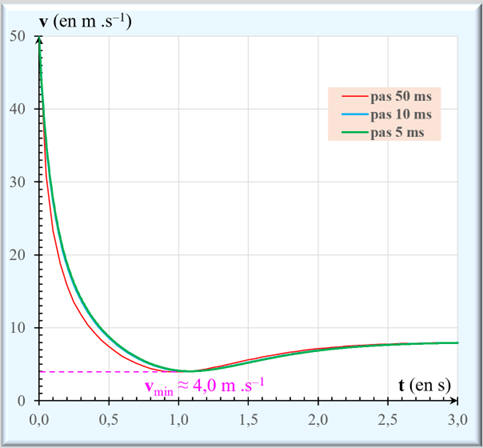
-
On peut changer l’échelle des
ordonnées.
e)-
Remarques :
-
On peut décomposer le mouvement du
volant de badminton en plusieurs phases
-
Première phase :
-
Le mouvement du volant de
badminton est rectiligne uniformément retardé.
-
La valeur du poids du badminton
est négligeable par rapport à la force de traînée.
-
La valeur de la vitesse diminue
rapidement.
-
Deuxième phase :
-
Le mouvement du volant de
badminton est curviligne décéléré .
-
La valeur du poids du badminton
n’est plus négligeable par rapport à la force de traînée.
-
La valeur de la vitesse diminue,
passe par une valeur minimale (sommet de la trajectoire).
-
vz = 0
et vx ≈ 4,0 m . s-1
-
Troisième phase :
-
Le mouvement du volant de
badminton est curviligne accéléré.
-
La valeur du poids du badminton
n’est pas négligeable par rapport à la force de traînée.
-
La valeur de la vitesse augmente
et tend vers une valeur limite vlim.
-
Quatrième phase :
-
Le mouvement du volant de
badminton est rectiligne uniforme (direction : verticale du lieu).
-
La valeur du poids est égale à la
valeur de la force de traînée : P =
f
-
v =
vlim ≈ 8,1 m . s-1
5-
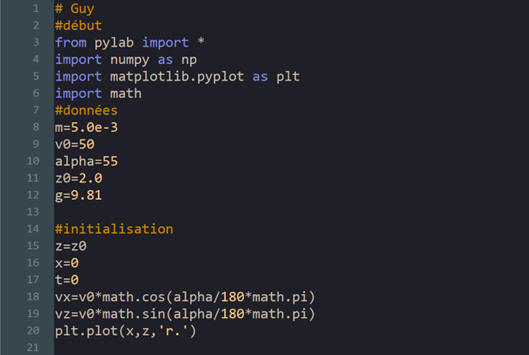
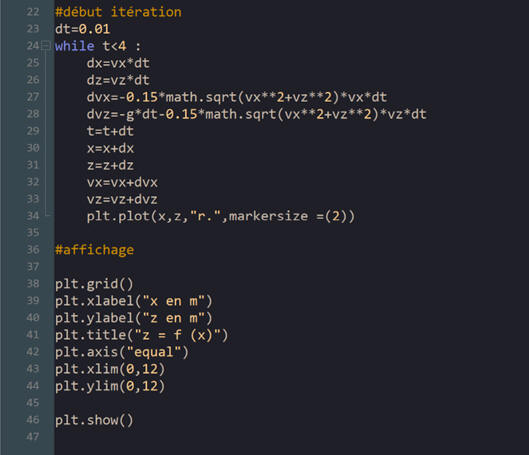
Exploitation avec Python.
a)- Programme Python : Pour le tracé de la trajectoire du volant de
badminton.
-
Mouvement d’un volant de badminton
avec Python (méthode d’Euler : δt = 10 ms)
-
On fait évoluer la valeur
du pas d’itération : δt = 10 ms
-
En
bleu : δt = 50 ms, en rouge
δt = 10 ms, en vert δt = 5 ms

-
Lorsque la valeur du pas du calcul δt
diminue, cela se traduit par une meilleure approximation de la solution.
-
Ainsi pour δt = 10 ms et
δt = 5 ms, on obtient pratiquement la même trajectoire.
-
La première partie de la
trajectoire est pratiquement la même pour les différents pas de calcul.
-
Ce qui change sensiblement :
-
la flèche ( zmax
≈ 10,56 m ; zmax
≈ 11,11 m ; zmax
≈ 11,18 m)
-
la portée ( xmax
≈ 11,54 m ; xmax
≈ 12,56 m ; xmax
≈ 12,62 m)
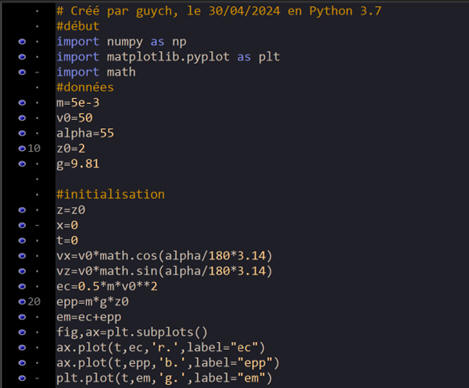
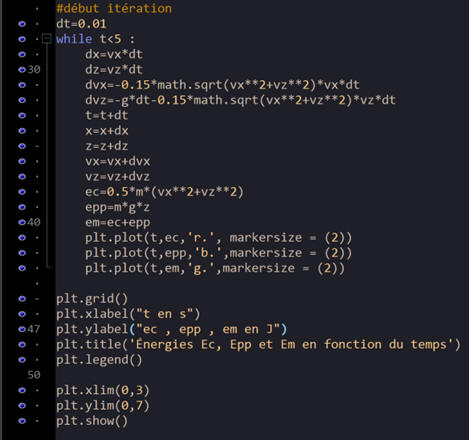
b)-
Programme Python pour le tracé
des énergies :
-
Le pas du programme est δt
= 10 ms
-
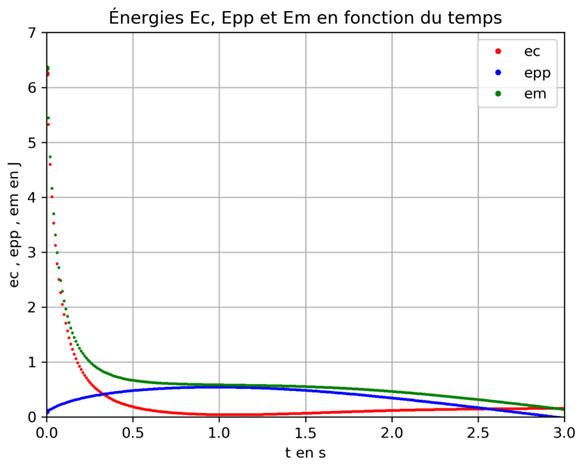
Tracé du graphe :
-
L’énergie cinétique
ec est maximale au
départ ;
-
Elle diminue rapidement puis plus
lentement ;
-
Elle passe par une valeur minimale
(sommet de la trajectoire)
-
Puis l’énergie cinétique augmente
et tend vers une valeur limite lorsque la vitesse limite est atteinte.
-
L’énergie potentielle
epp augmente au cours du
temps.
-
Elle passe par une valeur maximale
( sommet de la trajectoire)
-
Puis l’énergie potentielle diminue
au cours de la chute.
-
L’énergie mécanique
em diminue au cours du
temps, elle ne se conserve pas.
-
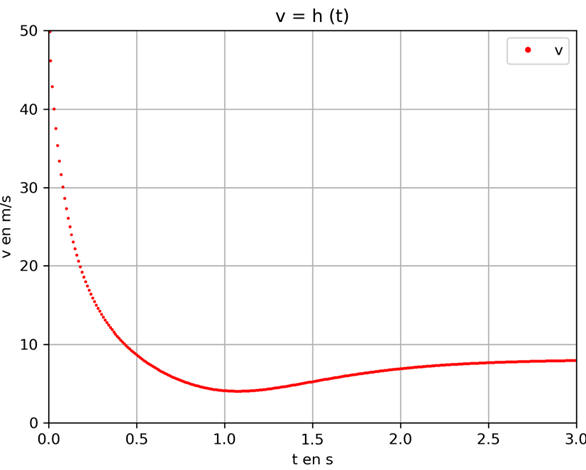
Courbe
v =
h (t) : pas du calcul δt = 10 ms.
Le volant de badminton : étude énergétique
DS : Classe de première
Le badminton : un sport dans le vent
Exercice

III- Exercice :
.
1)- Énoncé.

2)- Correction.

2)- Correction.


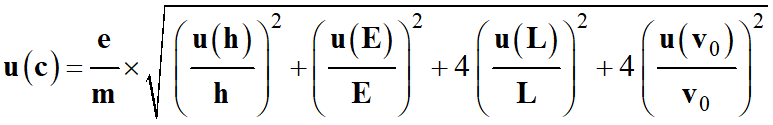


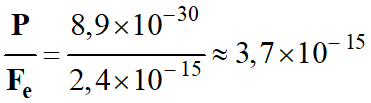
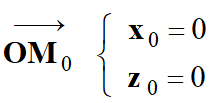
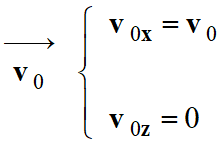
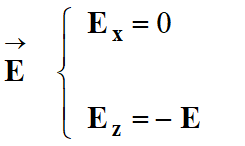
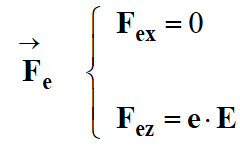

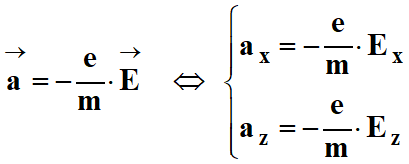
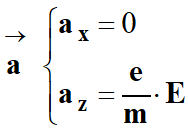
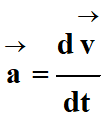
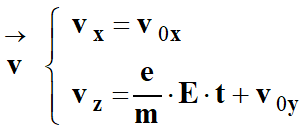
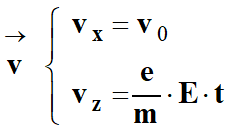
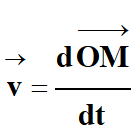 notation simplifiée
notation simplifiée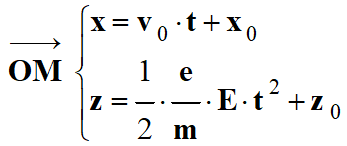
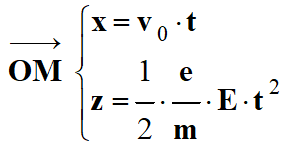
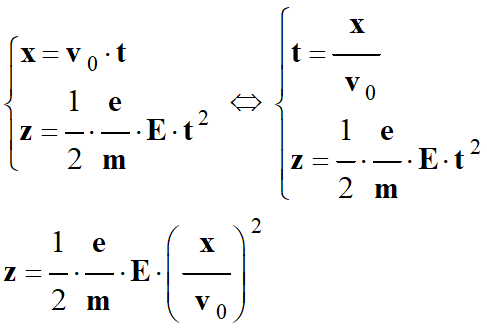
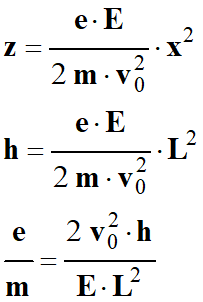
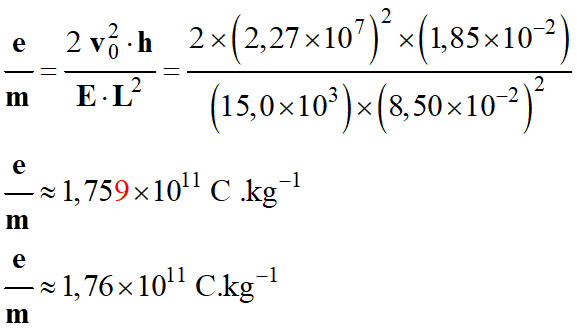
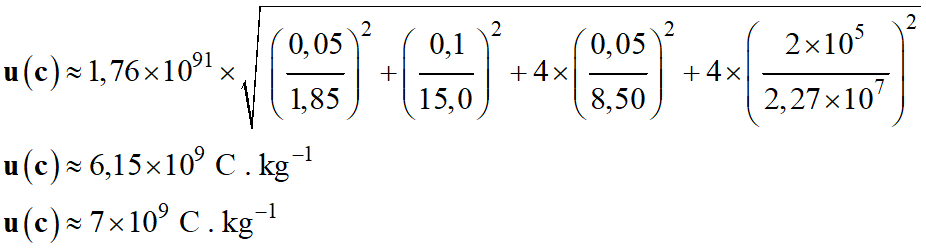
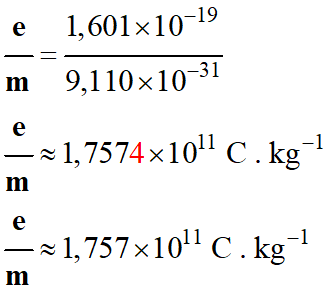



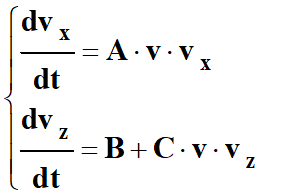

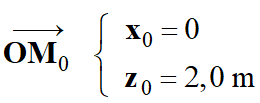
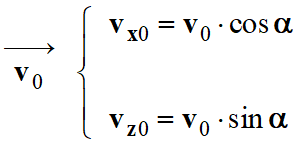
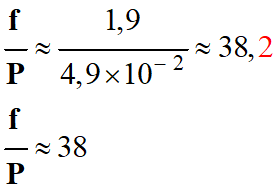


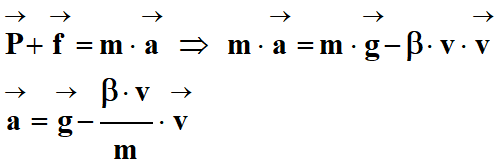
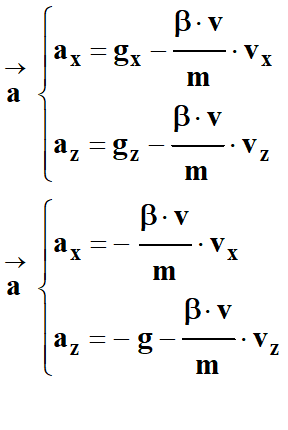
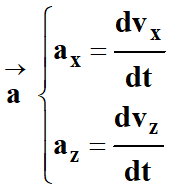
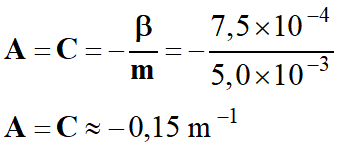





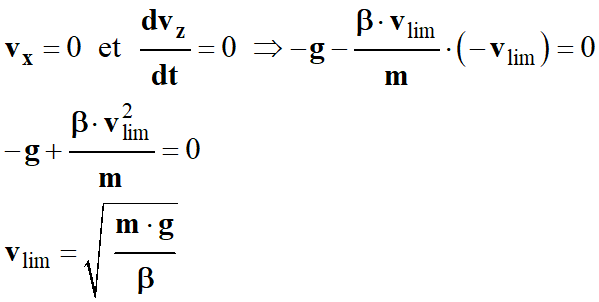
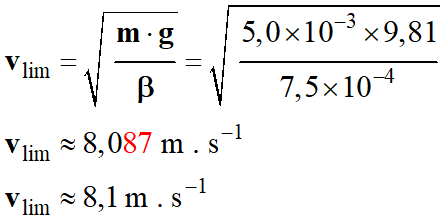
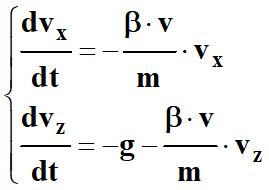
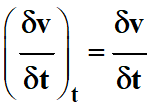
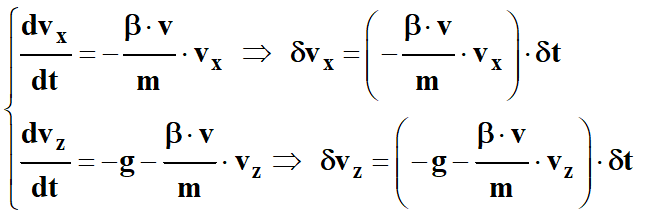 lorsque
lorsque