|
DS 01 Service et
réception au volley (30 min)
PARTIE 1 : Validité du service
Le service est effectué depuis la position B0 à la
vitesse v0 = 21,0 m . s–1.
Le service sera considéré comme valide à condition que le ballon
franchisse le filet sans le toucher et qu’il retombe dans le terrain adverse.
1.
Coordonnées du vecteur accélération du centre de
mase du ballon après la
frappe.
-
Énoncé de la deuxième loi de
Newton :
|
Dans un référentiel galiléen, la
somme des vecteurs forces
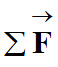 appliquées à un système
S, appliquées à un système
S,
de masse
m et de centre de
masse G,
est égal
au produit de sa masse
m par le vecteur
accélération
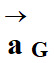 de son
centre de masse. de son
centre de masse.
|
|
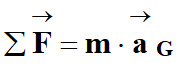
|
Valeur
des forces F en newton (N)
|
|
Valeur de
la masse m en kilogramme (kg)
|
|
Valeur de
l’accélération aG en mètre par
seconde
au carré (m . s–2)
|
-
Dans le cas présent :
-
Référentiel d’étude :

-
Système : le ballon de masse m.
-
On étudie le mouvement du centre de masse G
du ballon.
-
S = {m, G}
-
Le ballon est soumis uniquement à son poids :
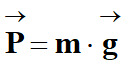
-
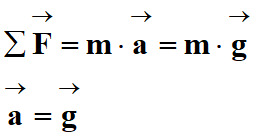
-
Le vecteur accélération
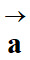 du ballon est
égal au vecteur accélération de la pesanteur
du ballon est
égal au vecteur accélération de la pesanteur
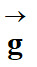 . .
-
Coordonnées du vecteur 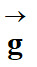 :
:
-
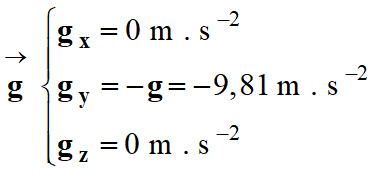
-
Coordonnées du vecteur accélération
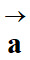 :
:
- comme :
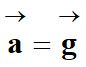
-
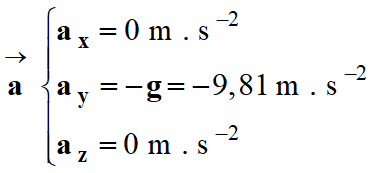
2.
Équations horaires du mouvement du centre de
masse du ballon :
-
Coordonnées du vecteur vitesse  : :
-

-
Équations horaires du vecteur vitesse
 du centre de masse
G : du centre de masse
G :
-
Dans un référentiel
R donné, le vecteur accélération
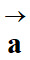 d’un point
M à l’instant t, est égal
à la dérivée , par rapport au temps, du vecteur vitesse
d’un point
M à l’instant t, est égal
à la dérivée , par rapport au temps, du vecteur vitesse
 à cet instant : à cet instant :
|
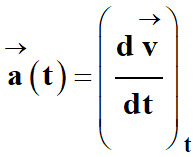
|
Ou plus
simplement
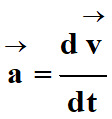
|
|
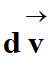
|
Valeur en
mètre (m . s–1)
|
|
dt
|
Valeur en
seconde (s)
|
|
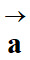
|
Valeur en
mètre par
seconde au carré (m . s–2)
|
-
La détermination du vecteur vitesse
nécessite de rechercher la primitive par rapport au temps de chaque coordonnée du vecteur accélération en tenant compte des
conditions initiales.
-
On cherche les primitives des équations
précédentes.
-
Il apparaît des constantes qui sont liées
aux conditions initiales.
-
Les constantes d’intégration apparues
dans les primitives sont liées aux conditions initiales : c’est-à-dire les coordonnées du vecteur vitesse
 à
l’instant initial. à
l’instant initial.
|
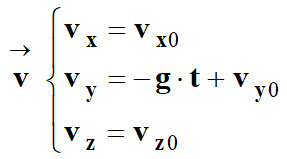
|
D’après
les
conditions
initiales
|
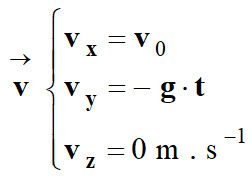
|
-
Équations horaires du mouvement :
-
On opère de la même façon :
-
Coordonnées du vecteur position à
l’instant initial :
-
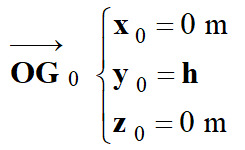
-
D’autre part :
-

-
Le vecteur vitesse
 est la dérivée par rapport au
temps du vecteur position est la dérivée par rapport au
temps du vecteur position
 . .
-
La détermination du vecteur position
nécessite de rechercher la primitive par rapport au temps de chaque coordonnée du vecteur vitesse en tenant compte des
conditions initiales.
|
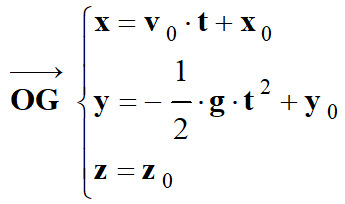
|
D’après
les
conditions
initiales
|
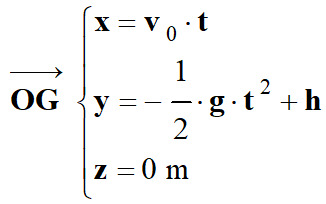
|
-
Ceci est bien en accord avec les formules
données dans l’énoncé.
-
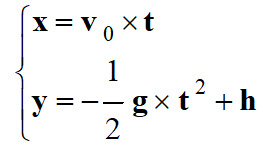
3.
Le mouvement du centre de masse du ballon est
plan.
-
Récapitulatif :
|
Vecteur position
|
Vecteur
vitesse
|
Vecteur
accélération
|
|
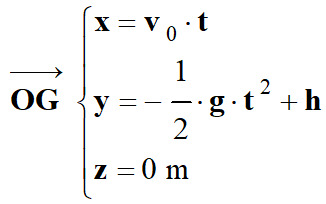
|
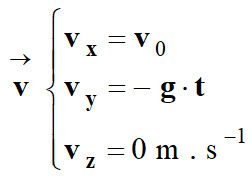
|
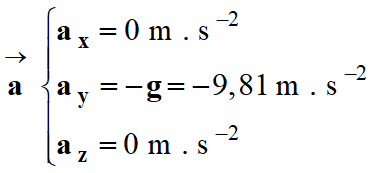
|
-
On remarque que les composantes
z = 0 m,
vz = 0 m . s–1
et az = 0 m . s–2.
-
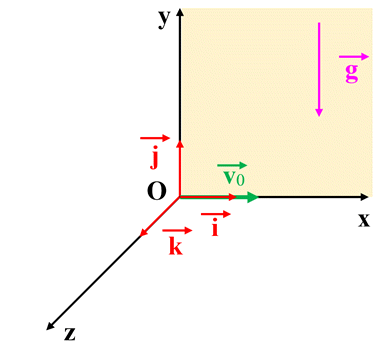
Le mouvement de
G est contenu dans le plan (Oxy)
appelé plan de tir.
-
Il contient le vecteur
 et le vecteur accélération et le vecteur accélération
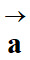 . .
4.
Équation de la trajectoire.
-
La trajectoire d’un point est l’ensemble
des positions successives occupées par ce point au cours du temps.
-
On
élimine le temps t pour
trouver la relation entre les coordonnées
x et
y du vecteur position.
-
Comme le mouvement a lieu dans le plan (Oxy)
:
-
y
= f (x).
|
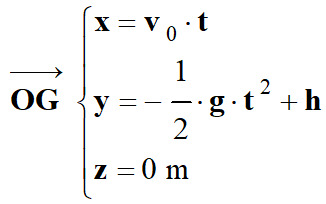
On en
déduit l’équation
de la trajectoire
|
|
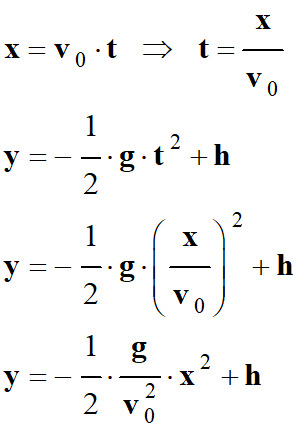
|
5.
Le ballon touche le
sol avant la ligne de fond.
-
Coordonnées du vecteur position lorsque
le ballon touche le sol :
-
Rayon du ballon de volley-ball :
r = 10 cm
-
On déduit de ceci que
ysol = 10 cm
-
Valeur de
xsol :
-

-
Comme
xsol <
L = 18,0 m, le ballon touche
le sol avant la ligne de fond.
-
Le ballon passe-t-il au-dessus du filet ?
-
Valeur de
yF pour
xF = 9,00 m
-
Hauteur du filet : H = 2,40 m
-
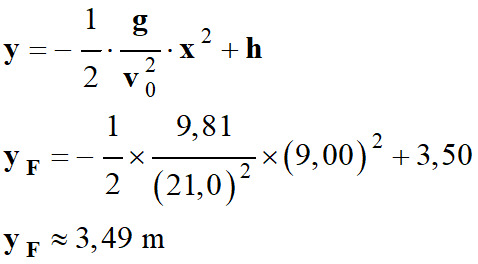
- yF > 2,50 m , le ballon passe
bien au-dessus du filet.
6.
Valeur vsol de la vitesse du
centre de masse du ballon lorsqu’il touche le sol.
-
Théorème de l’énergie cinétique :
|
La variation de l’énergie cinétique
d’un système
S en
mouvement, d’une
position A à une
position B,
est
égale à la somme des travaux de toutes
les forces appliquées au système
S entre
A et
B :
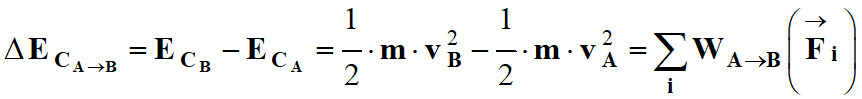
|
-
Dans le cas présent :
-
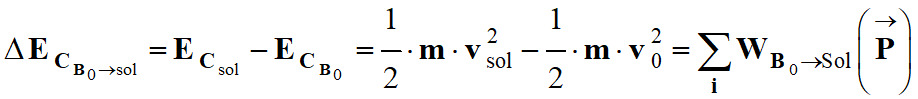
-
On considère que les forces de
frottements sont négligeables.
-

7.
Comparaison de la valeur vsol :
-
Explication :
- Lorsqu'un objet qui se déplace dans l’air est lourd et de petites dimensions,
on peut négliger les forces de frottements dues à l’air lorsqu’il se déplace sur une
courte distance.
-
Dans le cas présent, ces conditions
ne sont pas réunies.
-
Le ballon a un rayon de 10 cm, il est
léger et se déplace sur une distance de 18 m environ.
-
Comme les forces de frottements ne sont
pas négligeables, l’énergie mécanique ne se conserve pas et la vitesse vsol est
inférieur à celle trouvée précédemment.
PARTIE 2 : Réception du ballon par un joueur adverse.
-
Valeur de la vitesse moyenne minimale du
déplacement de ce joueur :
-
Ce résultat semble-t-il réaliste ?
-
Coordonnées du point
R de réception du ballon :
-
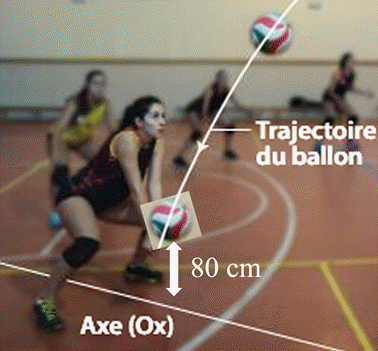
Le contact entre le ballon et le joueur
se fait en R situé à 80 cm
au-dessus du sol
-
Schéma de la situation :
-
Ordonnée du point
R :
-
yR
= 80 cm
-
Valeur de l’abscisse
xR du point R,
-

-
Valeur avec « trois chiffres
significatifs ». On peut garder deux chiffres significatifs.
-
Durée du parcours du ballon pour arriver
au point R :
-
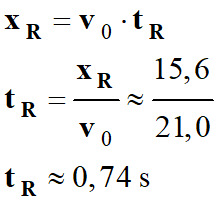 : :
-
Distance
d parcourue par le joueur
pendant tR :
-
Le joueur de l’équipe adverse est placé à
1,0 m de la ligne de fond du terrain :
-
d
≈ L – 1,0– 15,6
-
d
≈ 18,0 – 1,0– 15,6
-
d
≈ 1,4 m
-
Vitesse moyenne du joueur :
-

-
Ceci est tout à fait réalisable par le
joueur (cette vitesse correspond à une marche rapide).
|