|
|
Mouvement dans un champ uniforme Exercices |
|
|
|
|
|
QCM r Des champs uniformes Le mouvement dans un champ uniforme
|
1)- Exercice 04 page 250 : Caractériser le champ de pesanteur terrestre :
|
Caractériser le champ de pesanteur terrestre
1.
Donner la direction et le sens du champ de
pesanteur terrestre. 2.
Pourquoi le champ de pesanteur terrestre
est-il uniforme dans une région de l’espace de faibles dimensions ? |
|
Caractériser le champ de pesanteur terrestre
1.
Direction et le sens du champ de pesanteur
terrestre .
-
Le champ de pesanteur
-
Il est dirigé suivant la verticale du
lieu
-
Il est orienté vers le bas
-
Il a une valeur
g qui dépend de l’altitude et de la latitude du lieu considéré.
-
Schéma : 2.
Le champ de pesanteur terrestre est uniforme
dans une région de l’espace de faibles dimensions.
-
Au voisinage de la Terre, le champ de
pesanteur s’identifie au champ de gravitation si on néglige l’effet
de la rotation de la Terre autour de l’axe des pôles
-
La valeur de
g dépend de l’altitude et de la latitude
-
g = 9,81 N . kg–1
à Paris
-
Lorsque les dimensions sont de
l’ordre du kilomètre, on peut considérer que le champ de pesanteur
est uniforme.
-
Sa valeur diminue d’environ 0,3 % si
on s’élève de 10 km et sa direction varie d’environ 1° entre deux
points distants de 100 km. - En conséquence, dans une région de l’espace de faibles dimensions, - le champ de pesanteur garde
quasiment :
-
La même direction, le même sens et la
même valeur.
Interactions. Forces et Champs (Première programme 2018) Le champ de gravitation (Cours de terminale S : année 2000)
|
2)- Exercice 06 page 250 : Champ électrique dans un condensateur plan :
|
Champ électrique dans un condensateur plan : Entre deux plaques A et B, d’un condensateur plan, reliées à un générateur de courant continue, règne un champ électrique uniforme de valeur : E = 1,0 ×104 N . C–1. Les plaques sont distantes de d = 10,0 cm 1.
Calculer la valeur absolue |UAB|
de la tension appliquée entre les plaques. 2.
Comment varie la valeur du champ électrique
si la distance entre les plaques augmente ?
-
Données :
-
Valeur du champ électrique |
|
Champ électrique dans un condensateur plan : Schéma du dispositif :
1.
Valeur absolue |UAB| de la
tension appliquée entre les plaques.
-
Valeur du champ électrique
-
-
Application numérique :
-
-
Les unités :
-
(N . C–1) = (V . m–1)
-
Autre relation :
-
-
La tension aux bornes du
condensateur :
-
UAB > 0 - UAB ≈ 1,0 × 103 V 2.
Variation de la valeur du champ électrique
en fonction de d :
-
-
De cette relation, on peut déduire
que :
-
Lorsque
d ↑, alors la valeur du
champ E ↓.
-
La valeur du champ électrique
E entre les armatures du
condensateur plan est inversement proportionnelle
à la distance d entre
les armatures |
||||||||||||||||
3)- Exercice 08 page 251 : Représenter un vecteur accélération :
|
Représenter un vecteur accélération : Les coordonnées cartésiennes du vecteur accélération d’un point matériel M dans un repère orthonormé
-
1.
Représenter le vecteur accélération dans le
repère choisi. 2.
Calculer la valeur a de
l’accélération de M. |
Représenter un vecteur accélération :
-
Le vecteur accélération
-
Référentiel d'étude :
-
Coordonnées du vecteur accélération :
-
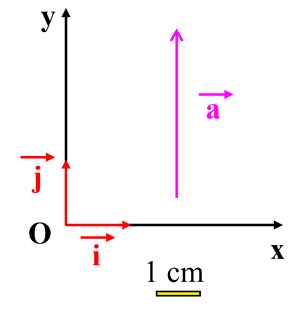
1.
Représentation du vecteur accélération dans
le repère choisi.
-
-
Échelle : 1 cm ↔ 2 m . s–2.
-
Le vecteur accélération ne dépend pas
du temps t.
-
Longueur du représentant du vecteur
accélération :
-
ℓa = 3,9 cm
2.
Valeur a de l’accélération de M.
-
Pour connaître les coordonnées du
vecteur accélération, on dérive le vecteur vitesse par rapport au
temps
Valeur du vecteur
accélération :
-

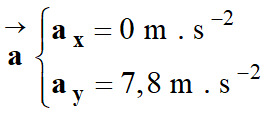
![]()
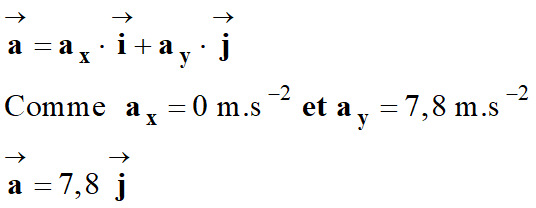
![]() a même direction et même sens que le vecteur
a même direction et même sens que le vecteur
![]()
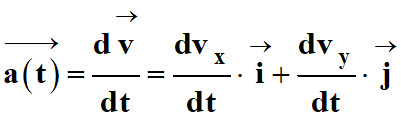
![]()
![]()
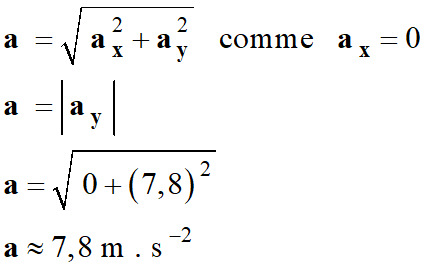
![]()
4)- Exercice 10 page 251 : Exprimer un vecteur accélération :
|
Exprimer un vecteur accélération : On étudie le mouvement du centre de masse d’une bille dans un
champ de pesanteur uniforme. Le mouvement de cette bille, soumise uniquement à son poids, est
étudié dans un référentiel terrestre supposé galiléen auquel on associe le repère
1.
À l’aide de la deuxième loi de Newton,
exprimer le vecteur accélération du centre de masse de la bille. 2.
Déterminer ses coordonnées cartésiennes.
-
Données :
g = 9,81 m . s–2. |
Exprimer un vecteur accélération : 1.
Expression du vecteur accélération
-
Énoncé de la deuxième loi de
Newton : Dans un référentiel galiléen, la
somme des vecteurs forces
de masse
m et de
centre de masse
G,
est
égal au produit de sa masse
m par le
vecteur accélération
Valeur des forces F en newton (N)
Valeur de la masse m en kilogramme (kg)
Valeur de l’accélération aG en mètre
par
seconde au carré (m . s–2)
-
Dans le cas présent :
-
Référentiel d’étude :
-
Système :
la bille de masse m.
-
On étudie le mouvement du centre de
masse G de la bille.
-
S = {m,
G}
-
La bille est soumise uniquement à son
poids
-
-
Le vecteur accélération
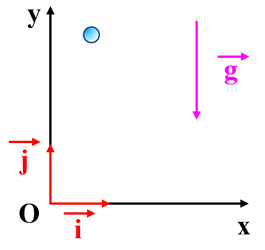
2.
Détermination des coordonnées cartésiennes
du vecteur accélération
-
Dans le référentiel :
-
Coordonnées du vecteur
-
-
-
![]() du centre
de masse de la bille.
du centre
de masse de la bille.
![]()
![]()
![]()

![]()
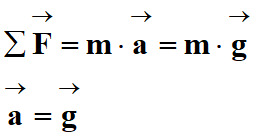
![]() de la bille
est égal au vecteur accélération de la pesanteur
de la bille
est égal au vecteur accélération de la pesanteur
![]() .
.![]() .
.
![]() :
: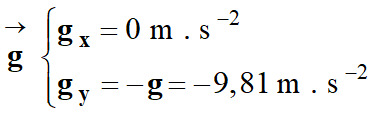
![]() :
: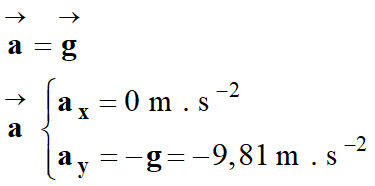
![]()
5)- Exercice 12 page 251 : Exprimer les conditions initiales :
|
Exprimer les conditions initiales : Une athlète lance un poids, assimilé à un point matériel, dans un
champ de pesanteur uniforme. On représente ci-dessous la situation du lancer à la date t
= 0 s.
1.
Dans quel référentiel le mouvement du poids
est-il étudié ? 2.
Exprimer les coordonnées cartésiennes du
vecteur position initiale
|
|
Exprimer les conditions initiales : 1.
Référentiel d’étude :
-
Référentiel terrestre supposé
galiléen :
-
2.
Coordonnées cartésiennes du vecteur position
initiale
-
Vecteur position initiale
-
-
Vecteur vitesse initiale
-
-
Le vecteur poids
-
|
6)- Exercice 14 page 252 : Exprimer le vecteur vitesse :
|
Exprimer le vecteur vitesse :
Les coordonnées cartésiennes du vecteur accélération d’un point
matériel M dans un repère orthonormé
-
1.
Déterminer les coordonnées cartésiennes du
vecteur vitesse de M dans le cas
où le vecteur vitesse initiale a
pour coordonnées :
-
2.
Montrer que le mouvement du point M
est plan. |
|
Exprimer le vecteur vitesse : 1.
Coordonnées cartésiennes du vecteur vitesse
de M:
-
Coordonnées cartésiennes du vecteur
vitesse initiale :
-
-
Coordonnées cartésiennes du vecteur
accélération d’un point matériel
M :
-
-
Référentiel d’étude : - Dans un référentiel R donné, le vecteur accélération d’un point M à l’instant t, est égal
à la dérivée , par rapport au temps, du vecteur vitesse
- La détermination du vecteur vitesse nécessite de rechercher la primitive par rapport au temps de chaque
coordonnée du vecteur accélération en tenant compte des conditions
initiales.
-
On cherche les primitives des
équations précédentes.
-
Il apparaît des constantes qui sont
liées aux conditions initiales. - Les constantes d’intégration apparues dans les primitives sont liées aux conditions initiales : c’est-à-dire les coordonnées du vecteur vitesse
2.
Montrer que le mouvement du point M
est plan.
-
Au cours du mouvement du point mobile
M, la coordonnée
vx = 0.
-
Le mouvement du point
M se fait dans le plan
(Oyz) contenant le
vecteur vitesse initiale
-
Ce plan est appelé, plan de tir.
-
Schéma :
|
7)- Exercice 16 page 252 : Établir l’équation de la trajectoire :
|
Établir l’équation de la trajectoire : Le graphique ci-dessous représente l’abscisse x et l’ordonnée y du centre de masse G d’une balle au cours du temps. Les équations horaires sont
précisées sur le graphique.
-
Graphique :
-
Établir l’équation cartésienne de la
trajectoire de G. |
|
Établir l’équation de la trajectoire :
-
Système :
S = {m,
M}
-
Référentiel d’étude :
-
Coordonnées cartésiennes du point
M :
-
-
Vecteurs position, vitesse et
accélération :
- Pour connaître les coordonnées du vecteur accélération, on dérive le vecteur vitesse par rapport au temps
- Récapitulatif :
-
Équation cartésienne de la
trajectoire de G :
-
On élimine le temps
t entre x et
y :
-
-
-
Représentation graphique de la
trajectoire :
-
y = – 0,293
x2 + 1,20
x + 2,27.
-
Représentation graphique de vx et
vy :
|
8)- Exercice 20 page 253 : Appliquer la conservation de l’énergie :
|
Appliquer la conservation de l’énergie : Pour servir au tennis, un joueur placé en O lance une
balle verticalement et la frappe en A à une hauteur H = 2,70
m au–dessus du sol. La balle part avec une vitesse horizontale de valeur v0 = 126 km . h–1 dans un référentiel terrestre supposé galiléen. De masse m, elle n’est soumise qu’à son poids. Schéma : 1.
L’énergie mécanique de la balle est-elle
constante ? 2.
Montrer que l’expression de la valeur vB
de la vitesse de la balle lorsqu’elle touche le sol s’écrit :
-
3.
Calculer sa valeur.
-
Donnée :
-
Intensité de la pesanteur :
g = 9,81 m . s–2. |
Appliquer la conservation de l’énergie :
-
Étude préliminaire :
-
OA =
H = 2,7 m
-
v0 = 126 km . h–1
-
Intensité de la pesanteur :
g = 9,81 m . s–2.
-
Système étudié : le centre de masse
G de la balle :
-
S = {m,
G}
-
Référentiel d’étude :
1.
Conservation de l’énergie mécanique de la
balle :
-
D’après l’énoncé : « De masse
m, elle n’est soumise
qu’à son poids »
-
-
Le poids est une force conservative,
-
en conséquence, l’énergie mécanique
de la balle se conserve.
-
L’énergie mécanique d’un système S
soumis à des forces conservatives est constante, elle se conserve.
-
Au cours du mouvement, la variation
de l’énergie mécanique : ΔEm = 0
-
ΔEC + ΔEP
= 0 =>
ΔEC = – ΔEP
-
Lorsqu’il y a conservation de
l’énergie mécanique, il y a transfert total de l’énergie potentielle
en énergie cinétique. 2.
Expression de la valeur vB
de la vitesse de la balle lorsqu’elle touche le sol :
-
Théorème de l’énergie cinétique : La variation de l’énergie
cinétique d’un système
S en
mouvement,
d’une
position A à
une position B,
est égale à la somme des travaux
de
toutes les forces appliquées au système
S entre
A et
B :
ΔECA→B
Variation de l’énergie cinétique en joule (J)
ECA et ECB
Énergie cinétique en joule (J)
m
La
masse en kilogramme (kg)
v
La
vitesse en mètre par seconde (m . s–1)
Travail de
la force
en joule (J)
F
Valeur de la force en newton
(N)
AB
Longueur du déplacement en mètre (m)
cos α
α
angle (rad ou °) entre les vecteurs
cos
α
: sans unité
-
Dans le cas présent, seulement le poids travaille :
-
-
On retrouve bien la relation donnée
dans l’énoncé.
-
3.
Valeur de la vitesse vB.
-

![]()
![]()
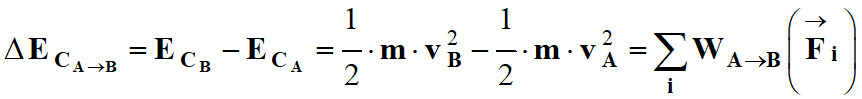
![]()
![]() et
et
![]()
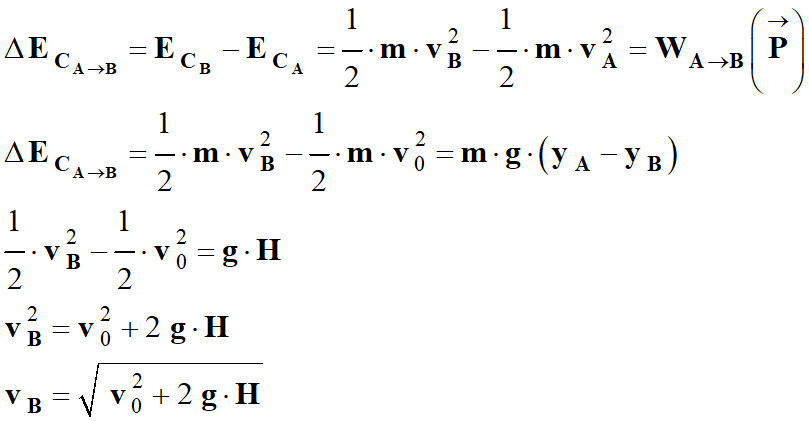
![]()

![]()
9)- Exercice 22 page 253 : Utiliser des équations horaires :
|
Utiliser des équations horaires : Dans un référentiel supposé galiléen, l’étude du mouvement du
centre de masse G d’un projectile conduit aux coordonnées cartésiennes suivantes :
-
-
1.
Écrire les coordonnées cartésiennes des
vecteurs vitesse et position de G au temps t = 0 s. 2.
À quelle date tS le
vecteur vitesse est-il horizontal ? 3.
Déterminer l’altitude atteinte par G
à cette date. |
Utiliser des équations horaires :
-
Étude préliminaire :
-
Système :
S = {m,
G}
-
Référentiel d’étude :
-
Coordonnées cartésiennes du point
G :
-
-
Coordonnées du vecteur vitesse du
point G :
-
-
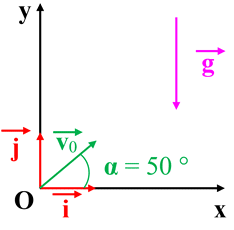
Trajectoire de
G :
-
On élimine le temps
t entre x et
y :
-
-
-
Équation de la trajectoire :
-
y ≈ – 0,47 x2
+ 1,2 x
1.
Coordonnées cartésiennes des vecteurs
vitesse et position de G au temps t = 0 s.
-
Vecteur vitesse à
t = 0 s :
-
-
Vecteur position au temps
t = 0 s :
-
2.
Date tS où le vecteur
vitesse est horizontal
-
-
Dans ce cas, la composant
vy est nulle :
-
-
Valeur de la vitesse au temps
tS.
-
3.
Altitude atteinte par G à cette date
tS.
-
Il faut déterminer la valeur de
l’ordonnée yS
au temps tS.
-
-
Abscisse du
xS au temps
tS.
-
xS ≈ 5,0 × cos
(50°) × tS
-
xS ≈ 5,0 × cos
(50°) × (0,39)
-
xS ≈ 1,25
m
-
xS ≈ 1,3 m
-
Trajectoire :

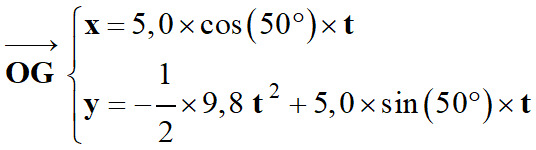
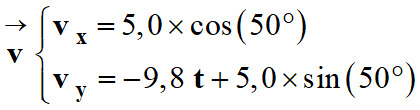
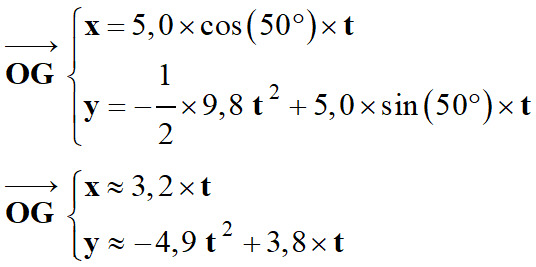
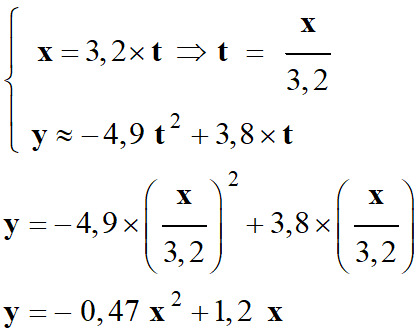
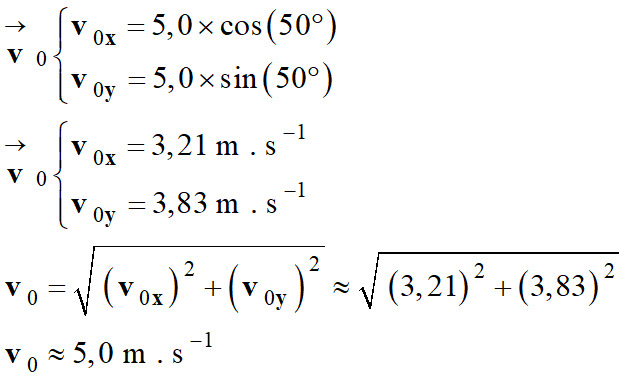
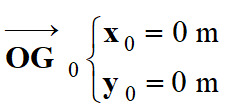
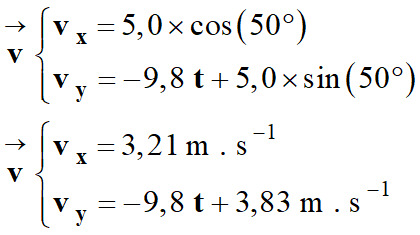
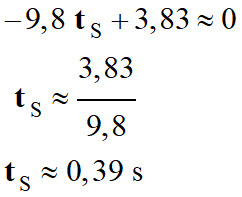
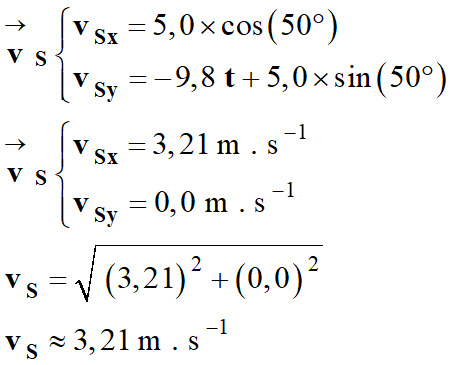
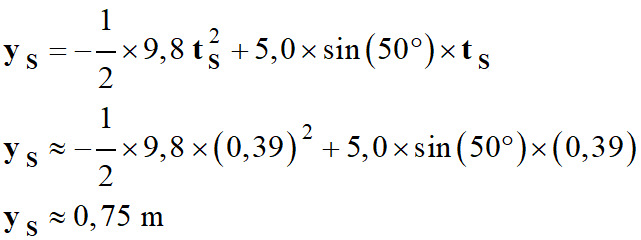
![]()
10)- Exercice 30 page 253 : Service au tennis :
|
Service au tennis : À l’instant t = 0 s, Ashleigh Barty frappe une balle de
tennis à une hauteur h = 2,80 m. Elle donne à cette balle une vitesse initiale
Le mouvement du centre de masse B de la balle de tennis
est étudié dans un référentiel terrestre supposé galiléen auquel on associe le
repère
Dans l’étude qui suit, on suppose que la balle est frappée sans effet et que toutes les actions dues à l’air sont négligées.
1.
Schématiser la situation. 2.
Établir l’expression du vecteur accélération
3.
Montrer que les équations horaires du
mouvement de ce centre de masse B sont :
-
4.
Montrer que l’équation de la trajectoire du
point B s’écrit :
-
5.
La balle passe-t-elle au-dessus du filet ?
-
Données :
-
Intensité de la pesanteur :
g = 9,81 m . s–2
-
Distance ligne de fond du
court-filet : L = 11,90 m
-
Hauteur du filet :
H = 0,92 m
-
Valeur de la vitesse initiale : v0 = 47,0 m .
s–1. |
|
Service au tennis :
-
-
1.
Schéma de la situation.
2.
Expression du vecteur accélération
-
Énoncé de la deuxième loi de
Newton :
-
Dans le cas présent :
-
Référentiel d’étude :
-
Système :
la bille de masse m.
-
On étudie le mouvement du centre de
masse B de la balle.
-
S = {m,
B}
-
La bille est soumise uniquement à son
poids
-
-
Le vecteur accélération
-
Coordonnées du vecteur
-
-
3.
Équations horaires du mouvement de ce centre
de masse B sont :
-
Équations horaires du vecteur vitesse
- Dans un référentiel R donné, le vecteur accélération d’un point M à l’instant t, est égal
à la dérivée , par rapport au temps, du vecteur vitesse
- La détermination du vecteur vitesse nécessite de rechercher la primitive par rapport au temps de chaque
coordonnée du vecteur accélération en tenant compte des conditions
initiales.
-
On cherche les primitives des
équations précédentes.
-
Il apparaît des constantes qui sont
liées aux conditions initiales. - Les constantes d’intégration apparues dans les primitives sont liées aux conditions initiales : c’est-à-dire les coordonnées du vecteur vitesse
-
On opère de la même façon :
-
-
Le vecteur vitesse
- La détermination du vecteur position nécessite de rechercher la primitive par rapport au temps de chaque
coordonnée du vecteur vitesse en tenant compte des conditions
initiales.
-
Ceci est bien en accord avec les
formules données dans l’énoncé.
-
4.
Équation de la trajectoire du point B
s’écrit :
-
La trajectoire d’un point est
l’ensemble des positions successives occupées par ce point au cours
du temps.
-
On
élimine le temps t pour
trouver la relation entre les coordonnées
x et
y du vecteur position.
-
Comme le mouvement a lieu dans le
plan (Oxy) :
-
y =
f (x).
-
Cette dernière relation est bien en
accord avec celle donnée dans l’énoncé.
-
5.
La balle passe-t-elle au-dessus du filet ?
-
Pour cela, il faut que pour
x = 11,90 m , yL
soit supérieur à 0,92 m.
-
Schéma de la situation :
-
-
En conséquence,
yL ≈ 1,23 m > 0,92 m
-
La balle passe au-dessus du filet. |
|
|