|
|
Aspects énergétiques |
|
|
|
|
|
I-
Théorème de l’énergie cinétique. 1)- Énergie cinétique d’un système. 2)- Travail d’une force constante. |
|
1)- Forces conservatives et non conservatives. |
|
III- La variation de l’énergie
mécanique. |
|
1)- Étude de la chute d’une bille dans un
fluide.
Le théorème de l’énergie cinétique
L’énergie mécanique La variation de l’énergie mécanique |
|
1)- Exercice 02 page 268 : Utiliser les unités :
2)- Exercice 04 page 268 : Calculer une énergie
cinétique
3)- Exercice 06 page 268 : Calculer le travail
d’une force.
4)- Exercice 08 page 268 : Calculer une variation
d’énergie cinétique.
5)- Exercice 10 page 269 : Caractériser le
travail d’une force.
6)- Exercice 11 page 269 : Calculer le travail
d’une force de frottement.
7)- Exercice 12 page 269 : Calculer une altitude.
8)- Exercice 14 page 269 : Exprimer une énergie
mécanique.
9)- Exercice 17 page 269 : étudier l’évolution de
l’énergie mécanique.
10)- Exercice 19 Page 270 : Freinage d’un
véhicule.
11)- Exercice 21 page 270 : chute libre ?
12)- Exercice 25 page 271 : énergie cinétique
d’une balle qui chute.
13)- DS 01 : Exercice 34 page 275 : Le badminton
(30 min)
14)- DS
02 : exercice 35 page 275 : Le pendule de Newton.
|
I-
Théorème de l’énergie
cinétique.
1)- Énergie cinétique d’un système.
-
L’énergie cinétique
est l’énergie que possède un solide du fait de son mouvement.
-
Elle dépend de la
vitesse et de la masse du solide.
-
Pour un solide animé
d’un mouvement de translation, tous les points du solide ont à chaque instant la
même vitesse que le centre d’inertie du solide :
-
L’énergie cinétique
EC
d’un système en mouvement de translation est égale au demi-produit de la masse
m
du solide par le carré de la vitesse
v2
du
système.
-
On écrit :
|
Relation |
Unités |
|
|
EC
en joule (J) |
|
m
en kilogramme (kg) |
|
|
v
en mètre par seconde (m . s–1 |
-
L’énergie cinétique
caractérise un système en mouvement.
-
Elle est
-
Proportionnelle à la
masse m du
solide
-
Proportionnelle au carré de la vitesse
v
du système.
-
Elle dépend du
référentiel d’étude.
2)- Travail d’une force constante.
a)-
Force constante 
:
-
Définition :
-
Une force
est
constante si :
-
Sa direction est
toujours la même ;
-
Son sens ne change
pas ;
-
Sa valeur n’est pas
modifiée.
b)-
Travail d’une force
constante :
|
Le travail d’une force
constante
|
- On note :
|
Relation |
|
|
Unités |
|
|
|
|
|
F
valeur de la force en newton
(N) |
|
|
AB
longueur du
déplacement en mètre (m) |
|
|
α
angle (rad ou °) entre les vecteurs
cos
α
: sans unité |
-
Schéma :
-
Application :
-
Premier chemin :
-
Calculer le travail de
la force
sachant
que : F
= 10,0 N,
ℓ
=
-
-
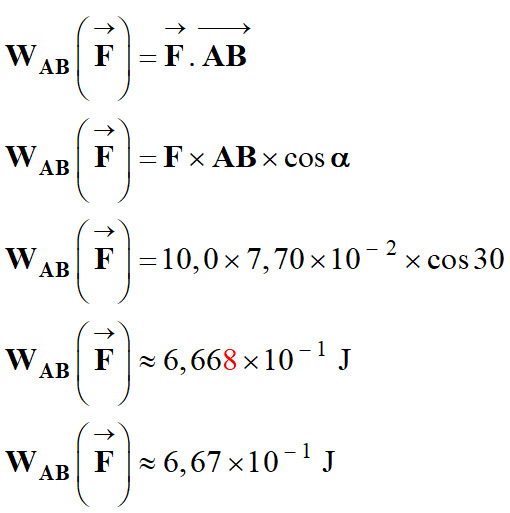
Deuxième chemin :
-
Calculer le travail de
la force
sur
le trajet AC puis sur le trajet CB.
-
Comparer les résultats
obtenus avec le résultat précédent et conclure.
-
Quelle remarque
peut-on faire ?
-
Déplacement
AC :
la force
fait un angle
α’ = 65,6 ° avec la direction du
déplacement
-
-
Déplacement
CB : La force
est
colinéaire au déplacement.
-
-
Troisième chemin : AEB
-
Déplacement
AE :
la force
fait un angle
α’ = 90 ° avec la direction du
déplacement
-
Le travail de la force
sur cette partie est nul :
- 
-
Déplacement
EB : La force
est
colinéaire au déplacement.
-
-
On remarque que :
-
-
D’autre part :
- 
-
Et enfin :
-
-
Conclusion :
-
-
Le
travail d’une force constante, lors du déplacement de son point d’application
M
entre A
et B ne
dépend pas du chemin suivi entre A
et B.
-
On est
en présence d’une force conservative.
c)-
Travail moteur et travail
résistant :
-
Si 0 ≤ α < 90 ° ,
alors cos α > 0 et
: le travail est moteur.
-
Si α = 90 ° , alors
cos α = 0 et 
: le travail est nul (le vecteur force est perpendiculaire au
déplacement).
-
Si 90 < α ≤ 180 ° ,
alors cos α < 0 et 
: le travail est résistant.
-
Une force travaille,
si son point d’application se déplace dans une direction qui n’est pas
perpendiculaire à celle de la force.
-
Une force ne travaille
pas si :
-
Sa direction est
perpendiculaire à la trajectoire de son point d’application.
-
Son point
d’application ne se déplace pas.
-
Exemple 1 :
-
Un mobile autoporteur
est placé sur une table à digitaliser horizontale.
-
À l’instant
t = 0 s, on lâche
le mobile autoporteur.
-
Il est entraîné dans
son mouvement par la masse marquée qui est accrochée au fil.
-
Faire le bilan des
forces appliquées au mobile autoporteur.
-
Quelles sont les
forces qui travaillent ?
-
Bilan des forces :
, la réaction du support
et
la tension du fil
-
Seule la force
travaille.
-
Les autres forces sont
perpendiculaires à la direction de déplacement du point d’application de la
force.
-
Exemple 2 :
-
Le mobile autoporteur,
maintenu par un fil tendu, est lancé sur la table à digitaliser.
-
La table est
horizontale.
-
Bilan des forces :
, la réaction du support
et
la tension du fil
-
Aucune force ne
travaille.
-
Les forces sont
perpendiculaires à la direction de déplacement du point d’application de la
force.
-
En résumé :
:
-
Une force dont le
point d’application se déplace peut mettre en mouvement un objet.
-
Elle peut modifier sa
vitesse, son altitude, sa température ou le déformer.
-
On dit que la force
travaille.
-
De plus, le travail
d’une force peut être moteur ou résistant.
3)- Travail de quelques forces constantes.
a)-
Travail du poids
-
On
considère le système S, de masse
m
qui se déplace du point
A au point
B.
-
Représentation
schématique :
-
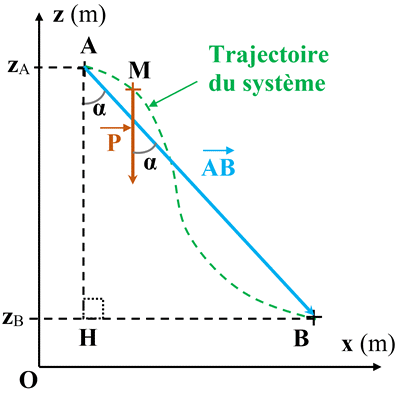
Le
système S
est soumis à son poids
(force
constante sur le domaine d’étude).
-
On peut utiliser la
relation précédente valable pour une force constante :
-
-
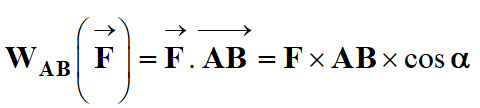
On applique cette
relation au poids
du
système :
-
|
Relation |
|
|
Unités |
|
|
P :
valeur de la force en newton
(N) |
|
|
(zA –
zB) :
altitudes des points A et B en mètre
(m) |
|
|
m :
masse du système en kilogramme (kg) |
|
|
g
facteur d’attraction terrestre :
g
= 9,81 N . kg–1 |
-
Conclusion :
|
- Lorsque qu’un système S de masse m passe d’un point A à un point B, le travail du poids ne dépend que de l’altitude zA du point de départ
et de
l’altitude zB
du point d’arrivée :
|
-
Remarques :
-
Si
zA
> zB, l’altitude du système S a diminué : le travail du poids est moteur.
-
Si
zA
< zB, l’altitude du système S a augmenté : le travail du poids est résistant.
-
Si
zA
= zB, l’altitude du système S n’a pas changé : le travail du poids est nul.
-
D’autre part, le
travail du poids ne dépend pas du chemin suivi.
-
Le poids
est une force conservative.
b)-
Travail d’une force de
frottement constante.
- Le système S se déplace de la position A à la position B.
- Au cours du déplacement le système
S
est soumis à une force de frottement constante
qui s’oppose au mouvement du
système S.
-
Schéma :
-
Calculer le travail de
la force
sachant
que : f =
10,0 N,
AB
=
-
La force de frottement
étant constante, on peut utiliser la relation précédente :
- 
-
Application
numérique :
-
-
Le travail de cette
force est résistant.
4)- Théorème de l’énergie cinétique.
a)-
Énoncé :
|
- La variation de l’énergie cinétique d’un système S en mouvement, d’une position A à une position B, est égale à la somme des travaux de toutes les forces appliquées au
système
S
entre A
et B :
|
-
Les unités :
|
|
Variation de l’énergie cinétique en joule (J) |
|
ECA et ECB |
Énergie cinétique en joule (J) |
|
m |
La masse en
kilogramme (kg) |
|
v |
La vitesse en
mètre par seconde (m . s–1) |
|
|
Travail de la force
en joule (J) |
|
F |
Valeur de la
force en newton (N) |
|
AB |
Longueur du
déplacement en mètre (m) |
|
cos α |
α
angle (rad ou °) entre les vecteurs
cos
α
: sans unité |
-
Remarque :
-
Le
travail des forces appliquées au système
S
peut faire varier l’énergie cinétique du système.
-
On dit que le travail
mécanique est un mode de transfert de l’énergie.
-
Si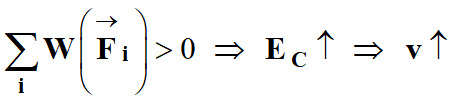 
-
Si la somme des
travaux des forces appliquées au système est positive, son énergie cinétique
augmente et la vitesse du système augmente.
-
Si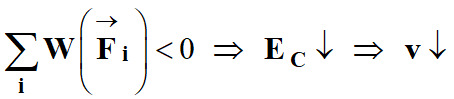 
-
Si la somme des
travaux des forces appliquées au système est négative, son énergie cinétique
diminue et la vitesse du système diminue.
b)-
Application :
-
Une bille d’acier de
masse m
=
-
La bille n’est soumise
qu’à son poids
.
-
À
quelle
hauteur h la
bille va-t-elle s’élever avant de retomber ?
-
On donne :
g =
-
Solution :
-
Référentiel d’étude :
le sol : référentiel terrestre supposé galiléen.
-
Le système d’étude :
la bille d’acier.
-
Bilan des forces : Le
poids
-
On peut considérer que
les autres forces sont négligeables devant le poids de la bille.
-
Schéma de la
situation :
-
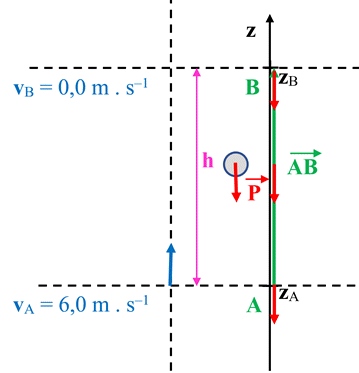
Au point
A, la bille est
animée de la vitesse vA = 6,0 m
/ s et au point B,
la bille est animée de la vitesse vB = 0,0 m
/ s.
-
On peut appliquer le
théorème de l’énergie cinétique à la situation décrite :
-
-
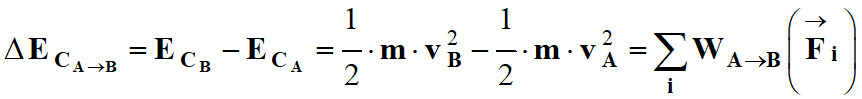
En conséquence :
-
-
Or :
-
-
Avec les notations
utilisées :
-
-
On peut donner
l’expression littérale de la hauteur h :
- 
-
Application
numérique :
- 
1)- Forces conservatives et non conservatives.
a)-
Définition :
-
Une
force appliquée à un système
S est conservative si son travail ne
dépend pas du chemin suivi.
-
Son travail dépend
seulement de la position de départ et de la position d’arrivée.
-
Elle ne dépend pas de
la trajectoire suivie entre les positions de départ et d’arrivée.
b)-
Cas du poids
d’un
système.
-
Ainsi, le poids
est
une force conservative.
-
Expression du travail
du poids :
|
- Lorsque qu’un système S de masse m passe d’un point A à un point B, le travail du poids ne dépend que de l’altitude zA du point de départ
et de
l’altitude zB
du point d’arrivée :
|
-
Le
travail du poids pour un déplacement du point
A
au point B dépend :
-
de
l’altitude zA
de l’altitude du point de départ
A
-
et de
celle de l’altitude zB
du point d’arrivée
B.
c)-
Cas d’une force de
frottement :
-
Les
forces de frottement ne sont pas conservatives car leur travail dépend de la
longueur du trajet entre les points
A
et B.
2)- Énergie potentielle de pesanteur d’un système.
-
À
chaque force conservative
, on associe une énergie appelée énergie potentielle ,
notée Ep.
|
- La variation d’énergie potentielle, lorsque le système S se déplace de la position A à la position B,
est égale à l’opposé du
travail de cette force conservative
qui s’applique sur le système entre les
positions A et
B :
-
On écrit :
-
|
-
Les unités :
|
|
Variation de l’énergie potentielle en joule (J) |
|
EPA et EPB |
Énergie potentielle en joule (J) |
|
|
Travail de la force
en joule (J) |
|
FC |
Valeur de la
force en newton (N) |
|
AB |
Longueur du
déplacement en mètre (m) |
|
cos α |
α
angle (rad ou °) entre les vecteurs
cos
α
: sans unité |
-
Cas du poids :
-
Le
poids
, étant est une force conservative, on lui associe une énergie potentielle
de pesanteur EP.
-
On
considère le système S, de masse
m
qui se déplace du point
A au point
B.
-
Représentation
schématique :
-
Expression de la
variation de l’énergie potentielle de pesanteur :
-
-
D’autre part, on
connaît l’expression du travail du poids lors de ce déplacement :
- 
-
On en déduit la
relation suivante :
-
-
-
Il découle de cette
expression :
-
EPB =
m
. g
. zB
et EPA =
m
. g
. zA
-
On peut
en déduire l’expression de l’énergie potentielle de pesanteur d’un système
S
de masse m
situé à l’altitude
z :
-
EP
= m
. g .
z
|
EP
= m . g . z |
EP :
énergie potentielle en joule (J) |
|
m
: masse du système en kilogramme (kg) |
|
|
z
: altitude du système en mètre (m) |
|
|
g
facteur d’attraction terrestre :
g = 9,81 N . kg–1 ou
g = |
-
Il existe une origine
des altitudes choisie comme référence :
-
De façon générale, on
choisit l’origine des altitudes qui simplifie les calculs.
-
À
l’altitude z = 0 m ,
EP
= 0 J.
-
L’axe
Oz
est orienté vers le haut.
-
Remarque 1 : La valeur
de l’énergie potentielle de pesanteur dépend de la valeur de
z, elle dépend du
choix de l’origine des altitudes.
-
L’énergie potentielle
est définie à une constante additive près.
-
La différence
d’énergie potentielle ne dépend pas du choix de l’origine.
-
Pour les exercices, on
choisit l’origine la plus commode, celle qui simplifie les calculs.
-
L’énergie potentielle de pesanteur d’un système de masse
m
est l’énergie qu’il possède du fait de son interaction avec la Terre.
-
LLa valeur de cette
énergie dépend de la position du système par rapport à la Terre.
3)- Énergie mécanique d’un système.
|
- L’énergie mécanique Em d’un système S de masse m est égale à la somme de son énergie cinétique EC
et de son énergie potentielle
EP.
-
Em
= EC
+ EP |
-
L’énergie mécanique Em
d’un système S
de masse m
dépend de la valeur de la vitesse
v
du système et de sa position dans le référentiel d’étude
III-
La variation de l’énergie
mécanique.
|
- La variation de l’énergie mécanique d’un système S en mouvement d’une position A à une position B est égale à la somme des travaux des
forces non conservatives
-
|
2)- Conservation de l’énergie mécanique.
-
Exemple :
étude de la
chute libre d’une balle de golf :
-
masse
m =
-
-
Référentiel d’étude :
le sol : référentiel terrestre supposé galiléen.
-
Le
système d’étude S : la bille d’acier.
-
Bilan des forces : Le
poids
(chute
libre)
-
Schéma de la
situation :
-
On applique le
théorème de l’énergie cinétique à la balle pour les deux positions
A et
B.
-
-
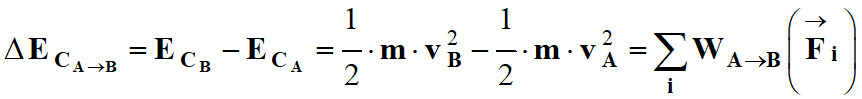
En conséquence :
- 
-
On peut donner
l’expression du travail du poids en utilisant l’altitude
z des points
utilisés :
-
-
Le travail du poids
sur le chemin AB
est égal à la différence d’énergie potentielle de pesanteur entre les altitudes
zA
et zB.
-
On peut écrire que :
-
-
La quantité
EC
+ EP est une constante au cours du temps, au cours du mouvement du système.
-
Cette quantité
représente l'énergie mécanique du système Em..
-
L’énergie mécanique
d’un système est la somme de son énergie cinétique et de son énergie
potentielle.
-
Relation :
Em.=
EC
+
EP.
-
Remarque 1 :
-
Lors de la chute
libre, l’altitude du système diminue, en conséquence, son énergie potentielle
diminue.
-
Simultanément, sa
vitesse augmente et de ce fait, son énergie cinétique augmente.
-
Remarque 2 :
-
Au cours du mouvement,
l’énergie potentielle se transforme en énergie cinétique et réciproquement.
-
Remarque 3 :
-
L’énergie mécanique
d’un système soumis uniquement à son poids reste constante.
-
Tableau de valeurs :
|
t |
x |
y |
h |
v |
Ec |
Ep |
Em |
|
s |
m |
m |
m |
m / s
|
J |
J |
J |
|
0,000 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00E+00 |
0,00E+00 |
0,00E+00 |
|
0,040 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00E+00 |
-2,00E-03 |
-2,00E-03 |
|
0,080 |
0,00 |
0,00 |
0,00 |
0,06 |
7,34E-05 |
0,00E+00 |
7,34E-05 |
|
0,120 |
0,00 |
-0,01 |
0,01 |
0,52 |
5,95E-03 |
-3,99E-03 |
1,96E-03 |
|
0,160 |
0,00 |
-0,04 |
0,04 |
0,87 |
1,66E-02 |
-1,80E-02 |
-1,38E-03 |
|
0,200 |
0,00 |
-0,08 |
0,08 |
1,27 |
3,53E-02 |
-3,40E-02 |
1,37E-03 |
|
0,240 |
0,00 |
-0,14 |
0,14 |
1,68 |
6,20E-02 |
-6,17E-02 |
2,76E-04 |
|
0,280 |
0,00 |
-0,21 |
0,21 |
2,09 |
9,59E-02 |
-9,19E-02 |
3,93E-03 |
|
0,320 |
0,00 |
-0,31 |
0,31 |
2,49 |
1,36E-01 |
-1,34E-01 |
2,32E-03 |
|
0,360 |
-0,01 |
-0,41 |
0,41 |
2,89 |
1,83E-01 |
-1,78E-01 |
5,59E-03 |
|
0,400 |
0,00 |
-0,54 |
0,54 |
3,30 |
2,40E-01 |
-2,34E-01 |
6,06E-03 |
|
0,440 |
0,00 |
-0,68 |
0,68 |
3,59 |
2,83E-01 |
-2,92E-01 |
-8,65E-03 |
|
0,480 |
-0,01 |
-0,83 |
0,83 |
3,93 |
3,39E-01 |
-3,57E-01 |
-1,85E-02 |
|
0,520 |
-0,01 |
-0,99 |
0,99 |
4,40 |
4,26E-01 |
-4,27E-01 |
-1,40E-03 |
|
0,560 |
-0,01 |
-1,18 |
1,18 |
4,88 |
5,23E-01 |
-5,09E-01 |
1,35E-02 |
|
0,600 |
-0,01 |
-1,38 |
1,38 |
5,25 |
6,06E-01 |
-5,96E-01 |
1,07E-02 |
|
0,640 |
-0,01 |
-1,60 |
1,60 |
5,63 |
6,96E-01 |
-6,91E-01 |
5,47E-03 |
|
0,680 |
-0,01 |
-1,83 |
1,83 |
6,00 |
7,92E-01 |
-7,90E-01 |
2,10E-03 |
|
0,720 |
-0,01 |
-2,08 |
2,08 |
6,50 |
9,30E-01 |
-8,98E-01 |
3,17E-02 |
|
0,760 |
-0,01 |
-2,35 |
2,35 |
|
|
|
|
-
Graphes : E
= f
(t) et
E
= f
(h)
-
Si un système est
soumis à son poids et à d’autres forces dont le travail est nul au cours du
mouvement, alors l’énergie mécanique de ce système est constante.
-
Remarque 4 : On a vu
que :
-
3)- Non conservation de l’énergie mécanique.
-
Exemple : Étude de la
chute d’une bille dans un fluide (TP Physique N° 08).
-
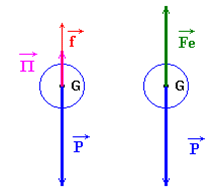
Au cours du mouvement,
la bille est soumise à son poids
, la poussée d’Archimède
et
à la force due
au frottement
qui apparaît lors de l’écoulement des couches de fluide l’une sur
l’autre.
-
Sur un graphe, on
représente les variations de l’énergie cinétique du système, l’énergie
potentielle de pesanteur et l’énergie mécanique du système.
-
Tableau de valeurs :
|
|
Pointages AviMéca |
|
|
|
|
|
|
|
|
t |
x |
y |
v |
EC |
EP |
Em |
|
N ° |
s |
m |
m |
m / s |
mJ |
mJ |
mJ |
|
0 |
0,00 |
0,00E+00 |
0,00E+00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
1 |
0,02 |
2,75E-04 |
-4,40E-03 |
0,27 |
0,15 |
-0,18 |
-0,03 |
|
2 |
0,04 |
-2,75E-04 |
-1,07E-02 |
0,37 |
0,28 |
-0,43 |
-0,15 |
|
3 |
0,06 |
-2,75E-04 |
-1,92E-02 |
0,48 |
0,46 |
-0,77 |
-0,31 |
|
4 |
0,08 |
-1,37E-03 |
-2,97E-02 |
0,56 |
0,63 |
-1,19 |
-0,55 |
|
5 |
0,10 |
-1,65E-03 |
-4,15E-02 |
0,64 |
0,84 |
-1,66 |
-0,83 |
|
6 |
0,12 |
-1,10E-03 |
-5,53E-02 |
0,71 |
1,02 |
-2,21 |
-1,19 |
|
7 |
0,14 |
-1,10E-03 |
-6,98E-02 |
0,76 |
1,16 |
-2,79 |
-1,63 |
|
8 |
0,16 |
-1,37E-03 |
-8,55E-02 |
0,81 |
1,32 |
-3,42 |
-2,10 |
|
9 |
0,18 |
-1,10E-03 |
-1,02E-01 |
0,84 |
1,43 |
-4,08 |
-2,65 |
|
10 |
0,20 |
-1,37E-03 |
-1,19E-01 |
0,88 |
1,56 |
-4,76 |
-3,20 |
|
11 |
0,22 |
-1,37E-03 |
-1,37E-01 |
0,90 |
1,65 |
-5,48 |
-3,83 |
|
12 |
0,24 |
-1,10E-03 |
-1,55E-01 |
0,90 |
1,65 |
-6,20 |
-4,55 |
|
13 |
0,26 |
0,00E+00 |
-1,73E-01 |
0,90 |
1,65 |
-6,92 |
-5,27 |
|
14 |
0,28 |
0,00E+00 |
-1,91E-01 |
0,93 |
1,75 |
-7,64 |
-5,90 |
|
15 |
0,30 |
-2,75E-04 |
-2,10E-01 |
0,93 |
1,75 |
-8,41 |
-6,66 |
|
16 |
0,32 |
-2,75E-04 |
-2,28E-01 |
0,93 |
1,75 |
-9,13 |
-7,38 |
|
17 |
0,34 |
0,00E+00 |
-2,47E-01 |
0,93 |
1,75 |
-9,89 |
-8,14 |
|
18 |
0,36 |
0,00E+00 |
-2,65E-01 |
0,95 |
1,84 |
-10,61 |
-8,77 |
|
19 |
0,38 |
2,75E-04 |
-2,85E-01 |
0,92 |
1,75 |
-11,41 |
-9,66 |
|
20 |
0,40 |
2,75E-04 |
-3,02E-01 |
0,93 |
1,75 |
-12,09 |
-10,34 |
|
21 |
0,42 |
2,75E-04 |
-3,22E-01 |
|
|
|
|
-
Graphe :
-
On remarque que
l’énergie cinétique du système augmente puis se stabilise.
-
L’énergie potentielle
de pesanteur diminue.
-
L’énergie mécanique du
système diminue aussi.
-
On peut utiliser le
théorème de l’énergie cinétique pour mettre en évidence ce phénomène :
-
Pour simplifier, on
peut remplacer la somme de la force
et
de la force
par
la force :
- 
-
L’application du
théorème de l’énergie cinétique entre deux positions
A et
B de son centre
d’inertie donne :
-
-
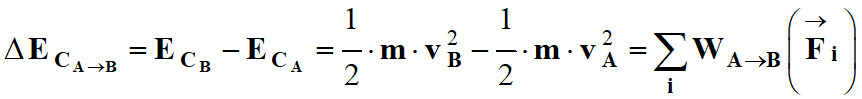
Ceci donne :
-
or
-
-
- ,La force , orientée vers le haut, est de sens opposé
au déplacement de la bille.
-
Son travail est
négatif.
-
En conséquence,
l’énergie mécanique de la bille diminue.
-
Conclusion :
-
l’énergie mécanique
d’un système soumis à des forces de frottement non compensées diminue.
1)- Étude de la chute d’une bille dans un fluide.
Le théorème de l’énergie cinétique
L’énergie mécanique
La variation de l’énergie mécanique
|
1)- Exercice 02 page 268 : Utiliser les unités :
2)- Exercice 04 page 268 : Calculer une énergie
cinétique
3)- Exercice 06 page 268 : Calculer le travail
d’une force.
4)- Exercice 08 page 268 : Calculer une variation
d’énergie cinétique.
5)- Exercice 10 page 269 : Caractériser le
travail d’une force.
6)- Exercice 11 page 269 : Calculer le travail
d’une force de frottement.
7)- Exercice 12 page 269 : Calculer une altitude.
8)- Exercice 14 page 269 : Exprimer une énergie
mécanique.
9)- Exercice 17 page 269 : étudier l’évolution de
l’énergie mécanique.
10)- Exercice 19 Page 270 : Freinage d’un
véhicule.
11)- Exercice 21 page 270 : chute libre ?
12)- Exercice 25 page 271 : énergie cinétique
d’une balle qui chute.
13)- DS 01 : Exercice 34 page 275 : Le badminton
(30 min)
14)- DS
02 : exercice 35 page 275 : Le pendule de Newton.
|
|
|
.
en
joule (J)
en
joule (J)
