|
|
Méthodes d'analyse physique Exercices |
|
|
|
|
|
QCM |
|
Méthodes
d’analyse physique
Les dosages par
étalonnage
La détermination
d’une quantité de gaz
La spectroscopie
|
1)- Exercice 04 page 40 : Utiliser la loi de Beer-Lambert :
|
Utiliser la loi de Beer-Lambert : La courbe ci-dessous représente l’absorbance A en fonction de la concentration C en diiode d’une gamme de solutions étalons. Dans les mêmes conditions de
mesure que celle de la gamme étalon, une solution S de diiode a une absorbance
AS = 1,25. Attention : il y a un
décalage de 0,5 mmol . L–1 sur le graphique du livre
1.
Énoncer la loi de Beer-Lambert. 2.
Dans quel domaine de concentration le graphe
traduit-il la loi de Beer-Lambert ? Justifier. 3.
Déterminer la
concentration CS en diiode de la solution
S. |
|
Utiliser la loi de Beer-Lambert :
1.
Loi de Beer-Lambert.
-
Relation :
-
ε (λ) est appelé coefficient d’extinction molaire ou coefficient
d’absorption molaire
-
Il dépend de la nature de
l’espèce dissoute et de la longueur d’onde de la radiation utilisée.
-
Écriture plus simple :
-
A =
k .
C 2.
Domaine de concentration et loi de
Beer-Lambert :
-
On remarque que pour une
concentration C < 2,5
mmol . L–1, les points sont sensiblement alignés.
-
La courbe obtenue est une droite qui
passe par l’origine.
-
L’absorbance
A de la solution de diiode est proportionnelle à la concentration
C, ce qui traduit bien la loi de Beer-Lambert.
-
Tableau de valeurs :
-
Il faut supprimer un certain nombre
de mesures pour le coefficient de détermination R2 soit proche de 1.
3.
Concentration CS en diiode
de la solution S.
-
Exploitation graphique :
-
CS ≈ 1,6 mmol
. L–1 |
2)- Exercice 05 page 40 : Exploiter la loi de Kohlrausch :
|
Exploiter la loi de Kohlrausch : Les conductivités σ de solutions de différentes
concentrations C en chlorure de calcium sont :
-
Tableau de valeurs :
Une solution
S0 de chlorure de calcium est diluée 100
fois. La conductivité de la solution diluée S est : σS = 2,25 mS . cm–1 1.
Tracer la courbe d’étalonnage σ =
f (C). 2.
La courbe traduit-elle la loi de
Kohlrausch ? Justifier. 3.
Déterminer les concentrations CS
et C0 en chlorure de calcium de S et S0. 4.
Justifier la dilution de la solution S0. |
|
Exploiter la loi de Kohlrausch : 1.
Tracer la courbe d’étalonnage σ =
f (C).
-
Tableau de valeurs :
-
Courbe d’étalonnage :
-
Les points sont sensiblement alignés.
-
La courbe obtenue est une portion de
droite qui passe par l’origine.
-
On peut tracer la droite moyenne et
déterminer sont équation.
-
Exploitation avec le tableur Excel :
-
Résultat mathématique :
-
y ≈ 0,270 ×
x
-
type :
y =
a ×
x
-
Traduction physique :
-
σ =
a ×
C
-
σ (mS
. cm–1) ≈ 0,270 ×
C (mmol
. L–1) (avec trois chiffres significatifs)
-
Le coefficient de proportionnalité :
coefficient directeur de la droite tracée
- 2.
La courbe et la loi de Kohlrausch :
- Dans le domaine de concentration étudié (C ≤ 10 mmol . L–1), la conductivité σ est proportionnelle à la concentration C des ions chlorure dans la solution, ce qui traduit bien la loi de Kohlrausch.
-
σ (mS
. cm–1) ≈ 0,270 ×
C (mmol
. L–1) - À partir de la mesure de la conductivité d’une solution en ions chlorure, on peut déterminer la
valeur de sa concentration. 3.
Concentrations CS et C0
en chlorure de calcium de S et S0.
-
La conductivité de la solution diluée
S est :
-
σS = 2,25 mS . cm–1
-
Méthode graphique :
-
CS ≈ 8,4 mmol
. L–1.
-
Avec l’équation de la droite
moyenne :
-
σ (mS
. cm–1) ≈ 0,270 ×
C (mmol
. L–1)
-
-
Concentration de la solution
C0 :
-
C0 = 100
CS
-
C0 ≈ 100 × 8,33 ×
10–3
-
C0 ≈ 0,833
mol . L–1 4.
Justification la dilution de la solution
S0.
-
La loi de Kohlrausch est valable pour
les solutions diluées.
-
La solution
S0 est trop
concentrée, il faut donc la diluer.
-
La concentration de la
solution : C ≤ 10 mmol . L–1 |
3)- Exercice 06 page 40 : Écrire l’expression d’une conductivité :
|
Écrire l’expression d’une conductivité : 1. Écrire l’expression littérale de la conductivité σ d’une solution aqueuse de nitrate d’argent {Ag+ (aq) + NO3– (aq)} en fonction des concentrations [Ag+ ] et [NO3–]
de des conductivités λ (Ag+) et λ (NO3–). 2. Par analyse dimensionnelle, déterminer l’unité dans laquelle doivent être exprimées les concentrations [Ag+ ] et [NO3–] sachant que la conductivité σ s’exprime en S . m–1
et que λ (Ag+) et λ (NO3–)
s’expriment en S . m2 . mol–1. |
Écrire l’expression d’une conductivité : 1.
Expression littérale de la conductivité σ
d’une solution aqueuse de nitrate d’argent {Ag+ (aq) + NO3– (aq)}
en fonction des concentrations [Ag+ ] et [NO3–]
de des conductivités λ (Ag+) et λ (NO3–).
-
σ =
λ (Ag+) . [Ag+ ] + λ (NO3–)
. [NO3– ]
-
Pour aller plus loin :
-
Dans la solution aqueuse de nitrate
d’argent :
-
[Ag+ ] = [NO3–
] = C
-
σ
= {λ (Ag+)
+ λ (NO3–)}
.
C 2.
Unité des concentrations [Ag+
] et [NO3–] :
-
Analyse dimensionnelle simplifiée :
-
[σ]
= (S . m–1) :
cette expression signifie que la conductivité s’exprime en S . m–1
-
[λ]
= (S . m2 . mol–1)
-
Or :
-
[σ]
=
[λ]
.
[C]
-
-
Il faut exprimer la concentration
C en mol . m–3.
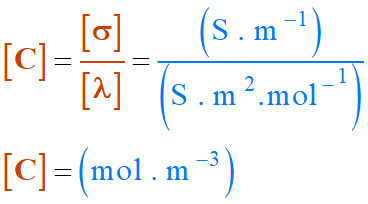
![]()
4)- Exercice 08 page 40 : Utiliser l’équation d’état du gaz parfait :
|
Utiliser l’équation d’état du gaz parfait : Le gonflage de certains airbags de voiture est assuré par du
diazote gazeux N2 (g). Lors du gonflage, une quantité n de diazote, considéré comme un gaz parfait, occupe un volume V = 90 L à la pression P = 1,3 × 105 Pa et à une température θ = 30 ° C. 1.
Écrire l’équation d’état du gaz parfait et
indiquer les unités de chacune des grandeurs. 2.
Calculer la quantité n de diazote.
-
Données :
-
R = 8,314 Pa . m3
.mol–1 . K–1 - T (K) ≈ 273 + θ ° C |
Utiliser l’équation d’état du gaz parfait : 1.
Équation d’état du gaz parfait et unités de
chacune des grandeurs.
-
Équation d’état du gaz parfait : P . V
= n . R . T
P
Pression en pascal (Pa)
V
Volume en mètre cube (m3)
n
Quantité de matière en mole (mol)
R
Constant des gaz parfaits : R = 8,314 Pa . m3
.mol–1 . K–1
T
Température absolue en kelvin (K)
-
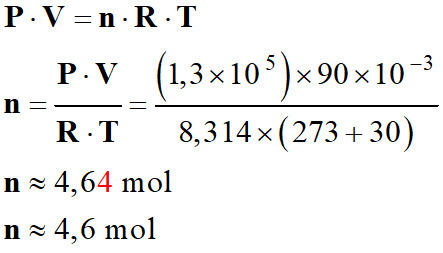
![]()
5)- Exercice 14 page 41 : Contrôle de qualité d’un produit :
|
Contrôle de qualité d’un produit : Un produit utilisé pour le nettoyage des lentilles de contact contient, comme seule espèce ionique du chlorure de sodium. Le fabricant indique : « chlorure de
sodium : 0,85 g pour 100 mL de solution »
La conductivité σ de solutions étalons de concentrations en quantité de matière C en chlorure de sodium est mesurée. Le graphe σ = f (C) est donné ci-dessous : La solution commerciale S0 est diluée 10 fois. La conductivité de la solution diluée S est σS
= 1,8 mS . cm–1. 1. Déterminer graphiquement la concentration CS en chlorure de sodium de la solution diluée S. 2.
Calculer la concentration C0
de la solution S0. 3.
En déduire sa concentration en masse t0. 4. À partir des indications de la notice, calculer la concentration en masse tnotice en
chlorure de sodium de la solution commerciale. 5.
Calculer l’écart relatif :
6. La concentration en masse t0 en chlorure de sodium de la solution S0 satisfait-elle au critère de qualité ?
-
Données :
-
M (NaCℓ)
= 58,5 g . mol–1 - Critère de qualité : le contrôle qualité est considéré comme satisfaisant si l’écart relatif est
inférieur à 5 %. |
|
Contrôle de qualité d’un produit : 1.
Concentration CS en
chlorure de sodium de la solution diluée S.
-
Les points sont sensiblement alignés.
-
La courbe obtenue est une portion de
droite qui passe par l’origine.
-
On peut tracer la droite moyenne et
déterminer sont équation.
-
Exploitation avec le tableur Excel :
-
Résultat mathématique :
-
y ≈ 0,1272 × x
-
type :
y = a × x
-
Traduction physique :
-
σ = a × C
-
σ (mS
. cm–1) ≈ 0,127 × C (mmol
. L–1) (avec trois chiffres significatifs)
-
Méthode avec l’équation de la
droite :
-
La conductivité de la solution diluée
S est σS = 1,8 mS . cm–1.
-
-
Méthode graphique :
-
La conductivité de la solution diluée
S est σS = 1,8 mS . cm–1.
-
2.
Concentration C0 de la
solution S0.
-
La solution commerciale S0
est diluée 10 fois.
-
C0 = 10 CS
-
C0 ≈ 10 × 14 × 10–3
-
C0 ≈ 0,14
mol . L–1 3.
Concentration en masse t0. - Un peu de révision : - La concentration molaire volumique C représente la quantité de matière n de soluté
dissoute dans un volume Vsol
= 1,0 L de solution.
-
Relation :
- Le titre massique t représente la masse m de soluté dissoute dans un volume Vsol = 1,0 L
de solution.
-
Relation :
-
Or
-
Relation :
-
Relation entre
t et C :
-
t =
C .
M
-
Concentration en masse (massique) ou
titre massique t0 :
-
t0 = C0 .
M (NaCℓ)
-
t0 ≈ 0,14 × 58,5
-
t0 ≈ 8,19
g . L–1
-
t0 ≈ 8,2 g . L–1 4.
Concentration en masse tnotice
en chlorure de sodium de la solution commerciale.
-
« chlorure de sodium : 0,85 g pour
100 mL de solution »
-
tnotice = 8,5 g . L–1 5.
écart relatif :
-
6.
Critère de qualité : - Le contrôle qualité est considéré comme satisfaisant si l’écart relatif est inférieur à 5 %.
-
En conséquence, la solution S0
satisfait au critère de qualité.
|
||||||||||||||||||||||||
6)- Exercice 16 page 42 : La tyrosine :
|
La tyrosine La L-tyrosine C9H11NO3 peut être consommée en complément alimentaire sous forme de gélules pour lutter contre le stress et l’anxiété.
A.
Spectre infrarouge de la
L-tyrosine. Le spectre infrarouge et la formule semi-développée de la
L-tyrosine sont données ci-dessous.
B.
Protocole expérimental. - Le tableau ci-dessous indique l’absorbance A, λ = 280 nm, de cinq solutions étalons de concentrations C en L-tyrosine.
- Soit S la solution obtenue.
-
AS = 1,0 1. En utilisant les bandes entourées de rouge sur le spectre infrarouge du document A. , montrer qu’il peut être celui
de la L-tyrosine. 2.
Une solution aqueuse de L-tyrosine est-elle
colorée ? Justifier. 3. La masse de L-tyrosine contenue dans la solution S est-elle cohérente avec l’indication de l’étiquette ?
-
Données :
-
Masse molaire : M
(tyrosine) = 181,0
g . mol–1.
-
Nom : acide
2-amino-3-(4-hydroxyphényl)propanoïque.
-
Bandes d’absorptions infrarouges :
|
|
La tyrosine 1.
Étude du spectre infrarouge du document A :
-
Spectre de la L-tyrosine :
-
Bande moyenne entre 3300 cm–1
et 3400 cm–1.
-
Cette bande est associée à une
liaison N – H d’une amine
-
Bande large et forte entre 2600 cm–1
et 3200 cm–1.
-
Cette bande est associée à la liaison
–O – H d’un acide carboxylique.
-
Bande fine et forte entre 1600 cm–1
et 1800 cm–1. - Cette bande est associée à la liaison C = O d’un acide carboxylique, mais aussi à la liaison
N – H d’une amine.
-
Ce spectre peut convenir pour la
L-tyrosine. - La tyrosine possède un groupe caractéristique amino NH2 et un groupe caractéristique carboxyle COOH. Elle appartient à la famille des α-acides aminés. - La molécule de tyrosine possède un seul atome de carbone asymétrique, marqué ci-dessous par un
astérisque. - La molécule est chirale et possède deux stéréoisomères qui sont des énantiomères.
-
La L ou
S (–)–tyrosine et la
D ou R (+)–tyrosine. - La tyrosine est présente dans de nombreux aliments (amande, avocat, banane, graine de citrouille, fève de Lima, etc.). - Elle peut être consommée en compléments alimentaires sous forme de
pour lutter contre le stress et l'anxiété 2.
Couleur de la solution aqueuse de
L-tyrosine. - Pour réaliser les mesures d’absorbance, le spectrophotomètre est généralement réglé sur la longueur d’onde λmax correspondant au maximum d’absorption du
spectre de la solution
étudiée. - À cette longueur d’onde, la valeur de l’absorbance étant la plus grande, l’incertitude sur la
mesure est la plus petite.
-
La longueur choisie :
λmax = 280 nm. Elle appartient au domaine des
UV.
-
La L-tyrosine absorbe dans le domaine
de UV,
-
Elle n’absorbe pas dans le visible,
λ < 400 nm.
-
La solution aqueuse de L-tyrosine est
incolore. 3.
Masse de L-tyrosine contenue dans la
solution S et l’indication
de l’étiquette :
-
Tableau de valeurs :
-
On connaît l’absorbance de la
solution S :
-
AS = 1,0 - Déjà, on peut affirmer que la valeur de la concentration en L-tyrosine de la solution S se situe entre
1,0 mmol . L–1 < C
< 1,5 mmol . L–1
-
Représentation graphique de
A = f (C). - On remarque que pour une concentration C < 2,5 mmol . L–1, les points sont
sensiblement alignés.
-
La courbe obtenue est une droite qui
passe par l’origine. - L’absorbance A de la solution S de tyrosine est proportionnelle à la concentration C, ce qui traduit bien la
loi de Beer-Lambert.
-
Exploitation graphique :
-
Concentration de la solution
S :
-
-
Quantité de matière de
nS L-tyrosine présente dans la solution
S :
-
nS =
CS .
VS
-
masse
mS de
L-tyrosine présente dans la solution
S :
-
mS =
nS . M
(tyrosine)
-
mS =
CS .
VS . M
(tyrosine)
-
mS = 1,32 × 10–3
× 2,00 × 181,0
-
mS ≈ 0,4778
g
-
mS ≈ 0,478 g
-
mS ≈ 478 mg
-
Indication portée par la bouteille :
-
Masse de tyrosine par gélule :
-
m = 500 mg - La masse de L-tyrosine contenue dans la solution S est cohérente avec l’indication de l’étiquette.
-
Critère de qualité :
-
- Le contrôle qualité est considéré comme satisfaisant si l’écart relatif est inférieur à 5 %.
-
En conséquence, la solution S
satisfait au critère de qualité.
-
Vérification :
-
Exploitation avec le tableur Excel :
-
On peut déterminer l’équation de la
droite tracée :
-
Résultat mathématique :
-
y ≈ 0,7337 × x
-
type :
y = a × x
-
Traduction physique :
-
A = a × C
-
A ≈ 0,734 × C (mmol
. L–1) (avec trois chiffres significatifs)
-
Méthode avec l’équation de la
droite :
-
L’absorbance de la solution S
est A = 1,0.
-
-
mS =
CS .
VS . M
(tyrosine)
-
mS = 1,4 × 10–3
× 2,00 × 181,0
-
mS ≈ 0,506 g
-
mS ≈ 0,51 g
-
Critère de qualité :
-
- Le contrôle qualité est considéré comme satisfaisant si l’écart relatif est inférieur à 5 %.
-
En conséquence, la solution S
satisfait au critère de qualité. - La masse de L-tyrosine contenue dans la solution S est cohérente avec l’indication de l’étiquette. |
|
|