QCM N° 07 Force des acides et des bases

QCM. N° 07	Force des acides et des bases

QCM N° 07

Force des acides et des bases

AIDE

Pour chaque question, indiquer la (ou les) bonne(s) réponse(s).

Énoncé

Soient les demi-équations

HCO₃^– (aq) + H⁺

= H₂CO₃ (aq)

HCO₃^– (aq)

= H⁺ + CO₃^2– (aq)

Les couples mis

en jeu sont :

HCO₃^– (aq)

H₂CO₃ (aq)

HCO₃^– (aq)

CO₃^2– (aq)

H₂CO₃ (aq)

HCO₃^– (aq)

CO₃^2– (aq)

HCO₃^– (aq)

H₂CO₃ (aq)

CO₃^2– (aq)

HCO₃^– (aq)

Soient les demi-équations

HCO₃^– (aq) + H⁺

= H₂CO₃ (aq)

HCO₃^– (aq)

= H⁺ + CO₃^2– (aq)

HCO₃^– (aq) est :

L’acide conjugué

H₂CO₃ (aq)

Un acide

au sens

de Brönsted

Une espèce

amphotère

On considère la réaction

H₂CO₃ (aq)

+ HO^– (aq)

→

HCO₃^– (aq)

+ H₂O (ℓ)

Cette réaction met en

jeu un transfert d’ion

hydrogène de :

HO^– (aq)

Vers

H₂CO₃ (aq)

Vers

HCO₃^– (aq)

H₂CO₃ (aq)

Vers

HO^– (aq)

Une solution d’acide

sulfurique

(2H₃O⁺(aq) + SO₄^2–(aq))

de concentration

C = 1,0 × 10^–2 mol . L^–1 :

Contient des

ions oxonium

à la

concentration

[H₃O⁺]_éq =

2,0 × 10^–2

mol . L^–1

a un pH

égal

à 2,0

a un pH

inférieur

à 2,0

Soient une solution

d’acide chlorhydrique

(H₃O⁺ (aq) + Cℓ^– (aq) )

et une solution

d’acide sulfurique

(2H₃O⁺(aq) + SO₄^2–(aq))

de pH = 2,00

Les deux

solutions ont

la même

concentration

en ions

oxonium

Les deux

solutions ont

la même

concentration

apportée

La solution

d’acide

sulfurique

contient plus

d'ions oxonium

que la solution

d’acide

chlorhydrique

On dilue dix fois une

solution d’acide

chlorhydrique

(H₃O⁺ (aq) + Cℓ^– (aq) )

de pH = 2,00

Le pH de

la solution

diminue

d’une unité

Le pH de

la solution

est divisé

par 10

Le pH de

la solution

augmente

d’une unité

La mesure du pH

d’une solution

N’est pas

sensible à

la température

Ne nécessite

pas l’étalonnage

préalable

du pH-mètre

Doit être

faite avec

une sonde

propre

et sèche.

On s’intéresse à la

réaction

N₂ + 3 H₂ → 2 NH₃

La transformation

est totale.

Son

avancement

maximal est

égal à son

avancement

final

N₂, H₂ et NH₃

sont présents

à l’état final

Le mélange

final ne

contient

que NH₃

On faite réagir

n₁ = 2,0 mol

de méthanoate d’éthyle

C₃H₆O₂ avec

n₂ = 2,0 mol

d’eau. On obtient

n₃ = 0,66 mol d’acide

méthanoïque CH₂O₂ et

n₄ = 0,66 mol

d’éthanol C₂H₆O.

Cette transformation :

Est totale

a un taux

d’avancement

final égal

à 33 %

a un taux

d’avancement

final égal

à 66 %

On fait réagir

n₁ = 2,0 mol

de méthanoate d’éthyle

C₃H₆O₂ avec

n₂ = 2,0 mol

d’eau. On obtient

n₃ = 0,66 mol d’acide

méthanoïque CH₂O₂ et

n₄ = 0,66 mol

d’éthanol C₂H₆O.

Dans l’état final de cette

transformation :

Le système

ne contient

que C₃H₆O₂

et H₂O.

Le système

est composé

de C₃H₆O₂,

C₂H₆O,

CH₂O₂

et H₂O.

Le système

ne contient

que C₃H₆O

et CH₂O₂.

On considère la réaction

HCOOH (aq)

+ NH₃ (aq)

HCOO^– (aq)

+ NH₄⁺ (aq)

Sa constante d’équilibre

s’écrit :

On considère un

système chimique

siège d’une réaction

non totale. Le

quotient de réaction

est supérieur à la

constante d’équilibre.

Le système

évolue

spontanément

dans le

sens direct

Le système

évolue

spontanément

dans le

sens indirect

L’équilibre

est atteint

À l’équivalence

d’un titrage :

On a apporté

juste assez

de réactif

titrant pour

consommer

tout le

réactif titré

initialement

présent

On a apporté

autant de

réactif titrant

qu’il y avait

initialement

de réactif titré

Le réactif

titrant et le

réactif titré

sont présents

dans les

proportions

stœchiométriques

On verse dans un

erlenmeyer un

volume V_A d’une

solution contenant

une espèce A de

concentration C_A.

On y ajoute

progressivement une

solution contenant

l’espèce chimique B

de concentration C_B

connue. L’équation

de la réaction support

du titrage est :

3 A + B → C + 2 D

De toutes les espèces

présentes, seule B est

colorée. Le volume

équivalent est V_E.

La quantité de matière

de B apporté

à l’équivalence est :

C_B . V_E

C_A . V_A

3 C_A . V_A

QCM réalisé avec le logiciel Questy

Pour s’auto-évaluer

AIDE

Chap N° 01 Transformations acido-basiques.

Couples acide / base :

- Un acide est une espèce chimique capable de céder au moins un ion hydrogène H⁺.

- L’acide AH se transforme alors en sa base conjuguée A^–.

- Écriture formelle :

AH (aq)	→	A^– (aq)	+	H⁺
Acide		Base		ion hydrogène

Acide et base selon Bronsted :

- Un acide est une espèce chimique capable de céder au moins un ion hydrogène H⁺.

- Une base est une espèce chimique capable de capter au moins un hydrogène H⁺.

- La base A^– se transforme alors en son acide conjugué AH.

Écriture formelle :

A^– (aq)	+	H⁺	→	AH (aq)
Base		ion hydrogène		Acide

- Couple acide / base :

- Écriture de la demi-équation du couple acide-base :

AH (aq)		A^– (aq)	+	H⁺
Acide		Base		ion hydrogène

- Signification :

- Le signe signifie que le transfert d’ion hydrogène H⁺ peut se produire dans les deux sens.

AH (aq)	→	A^– (aq)	+	H⁺
Ou bien
A^– (aq) + H⁺	→	AH (aq)

- Dans le cas présent :

H₂CO₃ (aq)	→	HCO₃^– (aq)	+	H⁺
Acide		Base		ion hydrogène

- Couple : H₂CO₃ (aq) / HCO₃^– (aq) :

HCO₃^– (aq)	→	CO₃^2– (aq)	+	H⁺
Acide		Base		ion hydrogène

- Couple : HCO₃^–) / CO₃^2– (aq)

Espèce amphotère : (point de vue acido-basique)

- Une espèce amphotère est à la fois l’acide d’un couple et la base d’un autre couple.

- Exemple :

Acide	Base
H₂O (ℓ)	/ HO^– (aq)
H₃O⁺ (aq)	/ H₂O (ℓ)

Acide	Base
H₂CO₃ (aq)	/ HCO₃^– (aq)
HCO₃^–(aq)	/ CO₃^2– (aq))

Réaction acido-basique :

- Une réaction acido-basique consiste à un transfert d'un proton entre l’acide A₁H d’un couple sur la base A₂^– d’un autre couple.

- Couple acide / base 1 : A₁H H⁺ + A₁^–

- Couple acide / base 2 : A₂H H⁺ + A₂^–

- Équation de la réaction :

- On se place dans le cas où l’acide A₁H réagit sur la base A₂^–

A₁H + A₂^– A₁^– + A₂H

A₁H + A₂^–→ A₁^– + A₂H

- L’équation s’écrit avec

- une double flèche si la réaction est non totale ;

- une simple flèche → si la réaction est totale.

- cette réaction met en jeu les couples acide / base suivants : A₁H / A₁^–et A₂H / A₂^–.

- Dans le cas présent :

HCO₃^– (aq)		CO₃^2– (aq)	+ H⁺
HO^– (aq) + H⁺		H₂O (ℓ)
HCO₃^– (aq) + HO^– (aq)	→	CO₃^2– (aq) +	H₂O (ℓ)

Solution aqueuse d’acide sulfurique : valeur du pH et concentration

- Pour préparer une solution d’acide sulfurique, on dissout une solution pure de H₂SO₄ (ℓ) (vitriol) dans l’eau.

- On verse toujours l’acide dans l’eau (la réaction est exothermique).

	eau
H₂SO₄ (ℓ) + 2 H₂O (ℓ)	→	2 H₃O⁺ (aq)	+	SO₄^2– (aq)
n solvant		0		0
0		2n / V		n / V
Concentration C		2 C		C

- On prélève une quantité de matière n de H₂SO₄ (ℓ)

- On prépare ainsi une solution de volume V par dilution :

- La concentration de la solution est C = n / V

- La solution contient des ions H₃O⁺ (aq) et des ions SO₄^2– (aq) :

- Avec [H₃O⁺] = 2n / V = 2 C et [SO₄²] = n / V = C

- Si C = 1,0 × 10^–2 mol . L^–1, alors [H₃O⁺] = 2,0 × 10^–2 mol . L^–1

- Le pH d’une solution est un indicateur d’acidité lié à la présence des ions oxonium H₃O⁺ (aq) en solution.

- Définition du pH :

Pour une solution diluée, [H₃O⁺] < 0,050 mol . L^–1,

Le pH est défini par la relation suivante :

Cette relation est équivalente à :

pH : grandeur sans unité

[H₃O⁺] : concentration en ions oxonium en mol . L^–1

C⁰ : concentration standard : C⁰ = 1,0 mol . L^–1

- Valeur du pH :

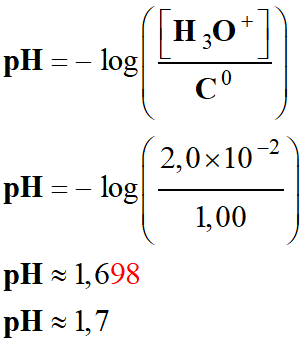
- Cas d’un acide fort dans l’eau :

- La transformation modélisée par la réaction entre l’acide AH (aq) et l’eau H₂O (ℓ) est totale :

- En conséquence :

- Le taux d’avancement de la réaction : τ = 1

- L’écriture de la réaction est la suivante :

AH (aq) + H₂O (ℓ)

→

H₃O⁺ (aq) + A^–(aq)

- La concentration en ions oxonium :

- [H₃O⁺]_f = [H₃O⁺]_max = C

- C représente la concentration en acide apporté.

- pH de la solution obtenue :

- pH = – log [H₃O⁺]_f

- Le pH d’une solution diluée d’acide fort, de concentration C en soluté apporté, est :

pH = – log C

Valable pour 10^–2 mol . L^–1 ≤ C ≤ 10^–6 mol . L^–1

- L’acide sulfurique est un acide fort dans l’eau :

H₂SO₄ (ℓ) + 2 H₂O (ℓ)

→

2 H₃O⁺ (aq)

SO₄^2– (aq)

Solution d’acide chlorhydrique et solution d’acide sulfurique : pH et concentration

- Le pH d’une solution diluée d’acide fort, de concentration C en soluté apporté, est :

pH = – log C

Valable pour 10^–2 mol . L^–1 ≤ C ≤ 10^–6 mol . L^–1

- L’acide chlorhydrique est un acide fort dans l’eau :

HCℓ (g) + H₂O (ℓ)

→

H₃O⁺ (aq)

Cℓ^– (aq) (aq)

- Définition du pH d’une solution aqueuse :

Pour une solution diluée, [H₃O⁺] < 0,050 mol . L^–1,

Le pH est défini par la relation suivante :

Cette relation est équivalente à :

pH : grandeur sans unité

[H₃O⁺] : concentration en ions oxonium en mol . L^–1

C⁰ : concentration standard : C⁰ = 1,0 mol . L^–1

- La concentration des ions oxonium peut se déduire de la définition du pH d’une solution aqueuse diluée :

- [H₃O⁺ ] = C⁰ . 10^–pH

- [H₃O⁺ ] = 1,0 × 10^{–
2,00}

- [H₃O⁺ ] ≈ 1,00 × 10^–2mol . L^–1

	eau
HCℓ (g) + H₂O (ℓ)	→	H₃O⁺ (aq)	+	Cℓ^– (aq)
n solvant		0		0
0		n₁ / V		n₁ / V
Concentration C₁		C₁		C₁
H₂SO₄ (ℓ) + 2 H₂O (ℓ)	→	2 H₃O⁺ (aq)	+	SO₄^2– (aq)
n solvant		0		0
0		2n / V		n / V
Concentration C		2 C		C

- C₁ = 2 C

- Les deux solutions n’ont pas la même concentration apportée :

Dilution d’une solution d’acide chlorhydrique :

- Acide fort dans l’eau :

- La transformation modélisée par la réaction entre l’acide AH (aq) et l’eau H₂O (ℓ) est totale :

- En conséquence :

- Le taux d’avancement de la réaction : τ = 1

- L’écriture de la réaction est la suivante :

AH (aq) + H₂O (ℓ)

→

H₃O⁺ (aq) + A^–(aq)

- La concentration en ions oxonium :

- [H₃O⁺]_f = [H₃O⁺]_max = C

- C représente la concentration en acide apporté.

- pH de la solution obtenue :

- pH = – log [H₃O⁺]_f

- Le pH d’une solution diluée d’acide fort, de concentration C en soluté apporté, est :

pH = – log C

Valable pour 10^–2 mol . L^–1 ≤ C ≤ 10^–6 mol . L^–1

- Le pH augmente d’une unité lorsque la concentration [H₃O⁺] est divisée par dix.

- Ceci, bien sûr, tant que 10^–2 mol . L^–1 ≤ C ≤ 10^–6 mol . L^–1

Mesure du pH d’une solution :

- Le pH-mètre :

- Il est nécessaire d’étalonner le pH-mètre avant toute mesure.

- L’étalonnage du pH-mètre nécessite l’utilisation de deux solutions étalons (solutions tampons) de pH connu.

- Il faut régler le bouton température sur celle de la solution dont on mesure le pH

- La mesure du pH dépend de la température

- Mesure du pH :

- Pour effectuer la mesure du pH d’une solution aqueuse, la sonde doit être rincée à l’eau distillée, essuyée puis plongée dans la solution étudiée.

- Après agitation et stabilisation de la mesure, la valeur du pH est relevée.

- Le pH-mètre :

- Montage pour un dosage pH-métrique :

La mesure du pH et sa précision :

- Dans les conditions habituelles, au lycée, on peut mesurer un pH, au mieux, à 0,05 unité près (le plus souvent à 0,1 unité près).

- Conséquences :

- Une mesure de pH effectuée à 0,05 unité près conduit à une valeur de la concentration [H₃O⁺] connue à 11,5 % près.

- Une simple mesure de pH ne peut donner une concentration avec précision.

- Il faut limiter le nombre de chiffres significatifs pour représenter une concentration déduite de la valeur du pH.

- Toute concentration déduite de la valeur du pH sera exprimée avec 2 chiffres significatifs au maximum.

Réaction totale, réaction non totale :

- Lorsqu’une réaction est totale, l’avancement final est égal à l’avancement maximal :

- x_f = x_max

- En présence d’un équilibre chimique (cas d’une réaction non totale) :

- x_f < x_max

Équation		N₂ (g) +	3 H₂ (g)	→	2 NH₃ (g)
état	Avanc. x (mol)	n (N₂) (mol)	n (H₂) (mol)		n (NH₃) (mol)
État initial	x	n₁	n₂		0
Au cours de la transformation	x	2 – x	n₂– 3 x		2 x
État final	x_f	n₁ – x_f	n₂ – 3 x_f		2 x_f
État max	x_max	n₁ – x_max	n₂ – 3 x_max		2 x_max

- si la réaction est totale, alors : x_f = x_max

- la présence ou non des réactifs en fin de réaction est liée aux quantités initiales des différents réactifs.

► Remarque :

- La réaction entre le diazote et le dihydrogène n’est pas une réaction totale.

- Elle donne lieu à un équilibre chimique :

- Tableau d’avancement de la réaction :

Équation		N₂ (g) +	3 H₂ (g)	2 NH₃ (g)
état	Avanc. x (mol)	n (N₂) (mol)	n (H₂) (mol)	n (NH₃) (mol)
État initial	x	2	3	0
Au cours de la transformation	x	n₁ – x	n₂– 3 x	2 x
État final	x_f	n₁ – x_f	n₂ – 3 x_f	2 x_f
État max	x_max	n₁ – x_max	n₂ – 3 x_max	2 x_max

Écriture de l’équation bilan :

Équation

N₂ (g) +

3 H₂ (g)

2 NH₃ (g)

- Mais dans l’énoncé de la question, on considère que cette réaction est totale.

- Dans le cas présent, il faut utiliser le fait que la réaction est totale.

- x_f = x_max

Réaction d’hydrolyse d’un ester : taux d’avancement

- Estérification et hydrolyse :

- Équation de la réaction : On est en présence d’un équilibre chimique.

	Estérification →
HCO₂H (ℓ)	+ C₂H₅OH (ℓ)	HCO₂ C₂H₅ (ℓ)	+ H₂O (ℓ)
Acide carboxylique	Alcool	Ester	eau
	← Hydrolyse

TP N° 10 Synthèse des esters

Équation		C₃H₆O₂ (ℓ) +	H₂O (ℓ)	CH₂O₂ (ℓ)	+ C₂H₆O (ℓ)
état	Avanc. x (mol)	n (C₃H₆O₂) (mol)	n (H₂O) (mol)	n (CH₂O₂) (mol)	n (C₂H₆O) (mol)
État initial	x	n₁ = 2,0	n₂ = 2,0	0	0
Au cours de la transformation	x	2,0 – x	2,0– x	x
État final	x_f	n₁ – x_f	n₂ – x_f	x_f = 0,66	x_f = 0,66
État max	x_max	n₁ – x_max	n₂ – x_max	x_max	x_max

- On en déduit la valeur de l’avancement final : x_f = 0,66 mol

- Dans le cas présent : n₁ = n₂ = 2,0 mol

- D’autre part, on peut calculer l’avancement maximal :

- x_max = n₁ = n₂ = 2,0 mol

- Taux d’avancement d’une réaction :

- Le taux d’avancement final d’une réaction, noté τ (tau), est le quotient de l’avancement final par l’avancement maximal :


τ (tau)	Taux d’avancement final (sans unité)
x_f	Avancement final (mol)
x_max	Avancement maximal (mol)

- Si τ = 0, la réaction n’a pas lieu.

- Pour une réaction totale : τ = 1 car x_f = x_max

- Pour une réaction non totale : 0 < τ < 1 car x_f < x_max

- On peut exprimer cette grandeur en pourcentage.

- Dans le cas présent :

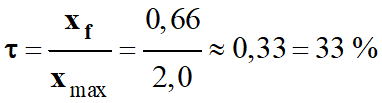
Réaction d’hydrolyse d’un ester : état final

Équation		C₃H₆O₂ (ℓ) +	H₂O (ℓ)	→	CH₂O₂ (ℓ)	+ C₂H₆O (ℓ)
état	Avanc. x (mol)	n (C₃H₆O₂) (mol)	n (H₂O) (mol)		n (CH₂O₂) (mol)	n (C₂H₆O) (mol)
État initial	x	n₁ = 2,0	n₂ = 2,0		0	0
Au cours de la transformation	x	2,0 – x	2,0– x		x
État final	x_f	1,32	1.32		0,66	0,66
État max	x_max	n₁ – x_max	n₂ – x_max		x_max	x_max

Transformation non totale. Équilibre chimique

Chap N° 07 Sens d’évolution spontanée d’un système chimique

- Comparer l’avancement final x_f et l’avancement maximal x_max permet de distinguer les transformations totales et non totales.

- Pour une transformation non totale, il faut connaître la valeur de l’avancement final x_f pour effectuer le bilan de matière à l’état final.

- Dans le cas d’une transformation non totale :

- À l’état final :

- Les quantités des espèces ne varient plus ;

- Tous les réactifs et les produits coexistent.

- On est en présence d’un équilibre chimique.

- Lors d’une réaction non totale :

- Les réactifs réagissent entre eux pour donner les produits ;

- Simultanément :

- Les produits réagissent pour donner les réactifs.

- Une réaction non totale est modélisée par deux réactions opposées l’une de l’autre.

- L’équation de la réaction s’écrit alors avec une double flèche qui traduit le fait que deux réactions, inverses l’une de l’autre, peuvent se produire simultanément dans le système.

- L’équation s’écrit alors :

a A + b B c C + d D

Quotient de réaction :

Chap N° 07 Sens d’évolution spontané d’un système chimique

- Quotient de réaction et sens d’écriture de la réaction :

- Considérons la réaction chimique non totale suivante :

a . A (aq) + b . B (aq) c . C (aq) + d . D (aq)

- Pour simplifier l’expression, on omet de mettre la concentration standard C⁰.

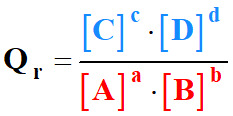
- Mais, il ne faut pas oublier que le quotient de réaction est une grandeur sans unité qui caractérise un système chimique dans un état donné :

- Exemple : réaction entre l’acide éthanoïque et l’eau :

CH₃COOH (aq)

H₂O (ℓ)

CH₃COO ^– (aq)

H₃O ⁺ (aq)

- Dans cette réaction, l’eau est le solvant.

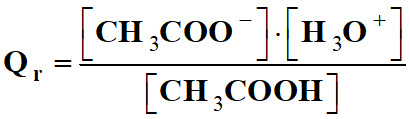
- Constante d’équilibre d’une réaction chimique :

- Dans l’état d’équilibre d’un système, le quotient de réaction Q_r,éq prend une valeur qui ne dépend pas de l’état initial.

- La valeur de Q_r,éq est indépendante de la composition initiale.

- Cette valeur ne dépend que de la température.

- Elle est appelée constante d’équilibre et on la note K.

- K = Q_r,éq

- La valeur de la constante d’équilibre nous renseigne sur la nature de la réaction chimique.

- Si K ≥ 10⁴ la transformation chimique est quasi-totale (on dit aussi totale).

- Si K ≈ 1 la transformation chimique est équilibrée.

- Si K ≤ 10^–4 la transformation chimique est très limitée.

- Exemple : Réaction entre l’acide éthanoïque et l’eau :

CH₃COOH (aq)

H₂O (ℓ)

CH₃COO ^– (aq)

H₃O ⁺ (aq)

- À l’équilibre chimique, on peut écrire :

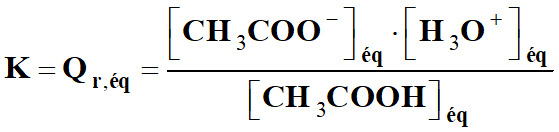
- Dans le cas de la réaction suivante :

HCOOH (aq)

NH₃ (aq)

HCOO ^– (aq)

NH₄⁺ (aq)

- Expression de la constante d’équilibre K :

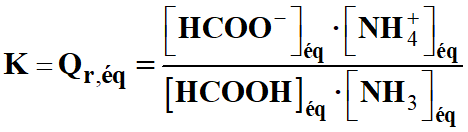
Quotient de réaction et constante d’équilibre :

Chap N° 07 Sens d’évolution spontané d’un système chimique

- Considérons la réaction suivante avec la terminologie associée :

Sens direct

a A (aq)

b B (aq)

c C (aq)

d D (aq)

Sens inverse

► Premier cas :

- Si le quotient de réaction initial Q_r,i est égal à la constante d’équilibre K,

- soit Q_r,i = K, le système est déjà à l’équilibre.

- Il n’évolue pas.

► Deuxième cas :

- Si le quotient de réaction initial Q_r,i est inférieur à la constante d’équilibre K,

- soit Q_r,i < K,

- Le système chimique évolue spontanément vers un état d’équilibre.

- Il évolue dans le sens direct de l’écriture de l’équation de la réaction.

► Troisième cas :

- Si le quotient de réaction initial Q_r,i est supérieur à la constante d’équilibre K,

- soit Q_r,i > K, le système chimique évolue spontanément vers un état d’équilibre.

- Il évolue dans le sens inverse de l’écriture de l’équation de la réaction.

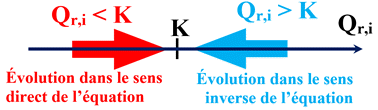
► Remarque :

- Ce critère d’évolution permet de prévoir le sens d’évolution spontanée du système connaissant sa composition initiale.

- Ce critère ne tient pas compte de l’aspect cinétique de la réaction.

Équivalence d’un titrage :

Les méthodes de suivi par titrage

Équivalence d’un titrage :

À l’équivalence, les réactifs sont dans

les proportions stœchiométriques définies

par les coefficients de la réaction.

À l’équivalence, il n’y a pas de réactif limitant.

- L’équivalence du titrage :

L’équivalence d’un titrage est atteinte lorsqu’on a réalisé

un mélange stœchiométrique des réactifs titré et titrant.

La relation à l’équivalence permet de déterminer

la quantité de réactif titré.

- Relation à l’équivalence :

Équation de titrage :	a A	+ b B	→	c C	+ d D
Quantités de matière à l’équivalence	n₀ (A)	n_E (B)
Coefficient stœchiométriques	a	b
Relation à l’équivalence

- On étudie le système avant l’équivalence, à l’équivalence et après l’équivalence.

Avant l’équivalence

Le réactif titrant est totalement consommé,

c’est le réactif limitant

Il reste encore du réactif titré : il est en excès.

À l’équivalence :

Le réactif titrant et le réactif titré sont totalement consommés.

Ils sont tous les deux limitants (mélange stœchiométrique).

Après l’équivalence

Le réactif titré est totalement consommé :

c’est le réactif limitant.

Maintenant, c’est le réactif titrant qui est en excès.

En conclusion

À l’équivalence du titrage,

il y a changement de réactif limitant

Quantité de matière et équivalence : Relation à l’équivalence

Équation		3 A	+ B	→	C	+ 2 D
état	Avanc. x (mol)	n (A) (mol)	n (B) (mol)		n (C) (mol)	n (D) (mol)
État initial	x	n₁	n₂		0	0
Au cours de la transformation	x	n_A – 3 x	n_B – x		x	2 x
État final	x_f = x_max	n_A – 3 x_f	n_B – x_f		x_f	2 x_f
Réaction totale

		Équation de la réaction de titrage
Équation		3 A	+ B	→	C + 2 D
État du système	Avanc.	n (A)	n (B)
État initial (mol)	x = 0	n₀ (A) = C_A . V_A	n (B) = C_B . V_B
Au cours de la transformation	x	C_A . V_A – 3 . x	C_B . V_B – x
État pour V_B < V_E			0 Réactif limitant
Équivalence V_B = V_E		0	0
Équivalence V_B = V_E		Mélange stœchiométrique
État pour V_B > V_E		0 Réactif limitant

- À l’équivalence :

- n_B = C_B . V_E

- Pour retrouver la relation à l’équivalence:

3 A	B
n (A) = C_A . V_A	n (B) = C_B . V_E
3	1

- C_A . V_A = 3 C_B . V_E