Pour aller plus loin : 

Mots clés :   Lois de Kepler ; le système solaire ; mouvements des planètes ;  mouvements des satellites  ; la force gravitationnelle ; ...

I- exercices  12 page 306.

1)- Signification de chaque terme.

2)- Unités des grandeurs physiques.

- Voir haut dessus.

3)- Schéma.

4)- Action de la Terre.

a)- Caractéristiques de la force gravitationnelle.

- 

b)- Valeur de la force :

- 

II- exercice 21 page 308.

1)- Caractéristiques du vecteur force.

- 

2)- Mouvement du satellite : le mouvement du satellite est circulaire dans le référentiel géocentrique.

3)- Le vecteur accélération :

- Dans le référentiel géocentrique, on applique la deuxième loi de Newton :

- 

- à chaque instant, le vecteur accélération a même direction, même sens que le vecteur force.

- Pour simplifier l’étude, on travaille dans le repère de Frenet :

- On remarque que .

- L’expression de l’accélération dans ce repère :

- 

- Dans le référentiel géocentrique, l’accélération du centre d’inertie du satellite est indépendante de sa masse. 

- Le vecteur accélération est radial et centripète.

4)- Caractéristiques du mouvement.

- Si la trajectoire du satellite est circulaire, alors :

- 

- puisque dans le cas d’un mouvement circulaire uniforme :

- 

- En identifiant :

- 

- Dans le référentiel géocentrique, le mouvement d’un satellite en orbite circulaire est uniforme.

- Sa vitesse dépend de l’altitude mais est indépendante de sa masse m.

- Valeur de la vitesse :

- 

5)- période de révolution : durée pour effectuer un tour.

- 

- Valeur de la période.

- 

III- exercice 22 page 309.

1)- Deuxième loi de Newton.

- Dans le référentiel géocentrique, on applique la deuxième loi de Newton :

- 

- à chaque instant, le vecteur accélération a même direction, même sens que le vecteur force.

- Pour simplifier l’étude, on travaille dans le repère de Frenet :

- On remarque que .

- L’expression de l’accélération dans ce repère :

- 

- Dans le référentiel géocentrique, l’accélération du centre d’inertie du satellite est indépendante de sa masse. 

- Le vecteur accélération est radial et centripète.

- Puisque la trajectoire du satellite est circulaire, alors :

- 

b)- expression de la vitesse du satellite dans le référentiel géocentrique.

- Dans le cas d’un mouvement circulaire uniforme :

- 

- En identifiant :

- 

- Période de révolution du satellite :

- 

c)- Ordre de grandeur de la valeur de la vitesse du satellite.

- 

2)-  

a)- La période de révolution d’un satellite géostationnaire est la même que celle de la Terre : T_S = T_T.

-  Le satellite se trouve à la verticale d’un même lieu. Son orbite est contenue dans le plan équatorial.

b)- La période ne dépend pas de la masse du satellite géostationnaire.

- La période dépend de l’altitude et l’altitude dépend de la vitesse du satellite.

c)- Tous les satellites géostationnaires ont la même vitesse car l’altitude h dépend de la vitesse et réciproquement.

3)-  

a)-  pour le satellite géostationnaire, h = 36000 km et pour le satellite SPOT, h’ = 830 km.

- Comme h > h’, v < v’ : la vitesse du satellite SPOT est plus grande que celle du satellite télécom.

b)- En conséquence, la période T’ du satellite SPOT est plus petite que la période T du satellite télécom.

c)- Le satellite SPOT n’est pas géostationnaire : h’ ≠ h.

IV- exercice 24 page 309. L’univers dans la balance.

 étude préliminaire.

1)-  

a)-  La grandeur r représente la distance du centre d’inertie de l’Astre de masse M au centre d’inertie du corps de masse m.

b)-  L’Astre de masse M est soumis à une force d’origine gravitationnelle de la part du corps de masse m.

- 

2)-  

a)- Le mouvement circulaire uniforme.

- Le repère de Frenet :

- 

-   désigne un vecteur unitaire tangent à la trajectoire et orienté dans le sens du mouvement.

-   désigne un vecteur unitaire perpendiculaire à et orienté vers le centre O du cercle.

- Le vecteur accélération peut se décomposer de la façon suivante :

- 

- R est le rayon de la trajectoire circulaire.

- En conséquence, le vecteur accélération peut être décomposé en une :

- Accélération tangentielle qui dépend de la variation de la valeur de la vitesse.

- Accélération normale qui est liée à la variation de la direction du vecteur vitesse.

- Dans le cas d’un mouvement circulaire uniforme :

- 

- Le corps est soumis à la force :

- La deuxième loi de Newton permet d’écrire :

- 

- Le mouvement de révolution circulaire est solution de la deuxième loi de Newton si :

- 

b)- La vitesse du satellite ne dépend pas de la masse. La vitesse du satellite n’est pas modifiée.

3)- Troisième loi de Kepler :

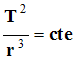
- Il faut trouver l’expression de la période :durée pour effectuer un tour.

- 

 Applications de la troisième loi de Kepler.

1)- Masse de la Terre.

- Par analogie, on peut écrire :

- 

2)- Valeur de la masse de Jupiter : il faut travailler avec un satellite de Jupiter, ici : Io.

- 

3)- Valeur de la masse du Soleil :

-  Il faut travailler avec un satellite du soleil, ici : Jupiter.

-