|
Chap. N° 05 |
Cinématique et dynamique newtoniennes. Cours. |
|
|
|
|
Exercices : énoncé avec correction a)-
Exercice 7 page 146 : Choisir un
référentiel d’étude. b)-
Exercice 10 page 146 : Connaître les
propriétés du vecteur accélération. c)-
Exercice 11 page 147 : Représenter des
vecteurs vitesses. d)-
Exercice 12 page 147 : Représenter des
vecteurs accélérations. e)-
Exercice 16 page 148 : Analyser un
mouvement. f)-
Exercice 18 page 148 : Déterminer des
forces inconnues. g)-
Exercice 28 page 150 : Voiture au banc
d’essai. h)-
Exercice 30 page 150-151 : Décollage
d’Ariane 5. i)-
Exercice 34 page 152 : En impesanteur. j)-
Exercice 35 page 153 : Le dauphin à
flancs blancs. |
I- Les
outils pour décrire le mouvement d’un objet.
-
Avant de décrire le mouvement
d’un objet, il faut préciser :
-
Le système S étudié
-
Et le référentiel
R
d’étude.
-
l'objet
dont on étudie le mouvement est appelé le
mobile et
l'objet de référence est appelé le référentiel.
-
Un référentiel est un
solide par rapport auquel on étudie le mouvement d'un
mobile.
-
Pour décrire le mouvement d'un
mobile, il faut indiquer le référentiel d'étude.
-
Un point matériel représente soit
un objet de petite taille (particule, petite bille), soit un
objet de grande taille dont on néglige les effets de rotation
sur lui-même.
-
Généralement, on appelle cet
objet le mobile.
-
Le système est modélisé par un
point unique (c’est le centre d’inertie
G du système), on
parle du modèle du point matériel de masse
m.
-
Lorsqu’on étudie le système
S
de masse m et de centre d’inertie
G, on utilise la
notation :
-
S = {m,
G}
-
Pour simplifier les écritures,
l’étude est limitée aux mouvements à deux dimensions, mais peut
être généralisée aux espaces à trois dimensions.
-
On travaille dans le repère
orthonormé
 lié au référentiel choisi.
lié au référentiel choisi.
-
L’association du repère avec le
référentiel d’étude est notée :

-
Le point
M
(x, y) est repéré grâce à ses coordonnées :
-
![]() ,
,
-
Les vecteurs
 sont des
vecteurs unitaires constants et
sont des
vecteurs unitaires constants et
![]()
-

-
Unités : les coordonnées
x
et y s’expriment en mètres (m).
-
Si le point M est en
mouvement, x et
y sont deux fonctions du temps.
-
Les expressions x
(t)
et y (t) sont appelées les équations horaires du
mouvement.
-
![]()
-
Pour simplifier et alléger les
notations, on peut écrire : ![]()
-
Tout en sachant que
x et
y sont des fonctions du temps
t.

a)-
Vitesse moyenne d'un point mobile.
Rappels.
-
La vitesse moyenne d'un point
mobile est égale au quotient de la distance parcourue par la
durée du parcours.
-
Relation :
|
|
Vitesse moyenne v
m en
m / s ou m
. s–1 |
|
Distance parcourue : d
en m |
|
|
Durée du parcours : Δt
en s |
-
Dans le S.I, l'unité de
vitesse est le mètre par seconde.
► Cas d'un mouvement rectiligne.
► Cas d'un mouvement curviligne.
-
C'est la vitesse à un instant
donné.
-
On définit cette vitesse afin de
mieux décrire le mouvement d'un point mobile.
-
On ne sait calculer qu'une
vitesse moyenne.
- On va considérer que pendant un intervalle de temps très court, la vitesse ne varie pratiquement pas, qu'elle reste pratiquement constante.
- On peut en
conséquence utiliser la relation précédente.
-
La vitesse instantanée
v (t)
d’un point mobile, à la date t, est pratiquement égale à
sa vitesse moyenne calculée pendant un intervalle de temps très
court encadrant l’instant t considéré.
-
Remarque
:
-
La valeur donnée par cette
relation est d'autant plus proche de la vraie valeur que la
durée Δt = t" - t' est petite.
-
Lorsque la durée
Δt
devient très petite, on la note τ.
c)-
Le vecteur vitesse.
-
La connaissance de la valeur de la vitesse instantanée
n’est pas insuffisante pour caractériser le mouvement d'un point
mobile.
-
Pour caractériser le mouvement d’un point mobile, il faut
connaître à chaque l’instant, la valeur, la direction et le sens
de la vitesse instantanée.
-
L'outil mathématique qui permet d'indiquer une direction,
un sens et une valeur est le vecteur.
-
On utilise en physique le vecteur
vitesse instantané noté
 .
.
► Le vecteur vitesse instantanée a
les caractéristiques suivantes :
-
Origine : position occupée par le point mobile à
l'instant considéré
t.
-
Direction : tangente à la trajectoire au point
considéré.
-
Sens
: celui du mouvement à cet instant
-
Valeur : celle de la vitesse instantanée à cet
instant.
► Représentation du vecteur
vitesse.

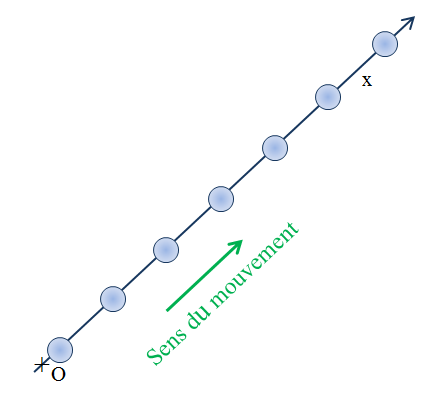
-
On représente le vecteur vitesse
par un segment fléché :
-
Vecteur vitesse du point mobile
M
à l'instant t3,
![]() que l'on
note plus simplement
que l'on
note plus simplement
![]() .
.
![]() Pour tracer ce vecteur vitesse :
Pour tracer ce vecteur vitesse :
|
-
Origine
:
Position occupée par le point mobile à l'instant
considéré t c'est-à-dire le point M3. -
Direction :
Tangente à la trajectoire au point considéré :
droite parallèle à (M2 M4)
issue de M3. -
Sens
: Celui
du mouvement à cet instant -
Valeur : Celle
de la vitesse instantanée à cet instant : -
-
Longueur du
représentant ℓv :
- Une échelle de représentation est indispensable. - Elle associe la
longueur du segment fléché à la valeur de la vitesse
instantanée. - Exemple : 1 cm ↔ 0,1 m / s. - En conséquence si v3 ≈ 0,40 m / s,
-
Le segment fléché
aura une longueur : ℓv3 = 4 cm. |
Animation CabriJava (Tracé de vecteurs vitesses)
![]() Récapitulatif :
Récapitulatif :
- Caractéristiques du vecteur vitesse
instantanée au temps t3.

|
|
|
|
|
|
|
|
|
|
|
-
C’était une approche
expérimentale qui permettait d’atteindre la valeur de la vitesse
instantanée et de tracer le vecteur vitesse instantanée.
-
La relation vectorielle approchée
était de la forme :
-
 (1)
(1)
d)-
Le vecteur vitesse instantanée.
-
Pour simplifier l’étude, on
considère le mouvement d’un objet sur une table plane inclinée
ou pas.
-
On étudie le mouvement de l’objet
par rapport à la table (Référentiel).
-
À ce référentiel, on associe le
repère :
 .
.
-
On écrit la relation (1), en
utilisant l’origine des espaces O.

-

-
Le vecteur vitesse traduit les
variations du vecteur position par rapport au temps.
|
Définition
du vecteur vitesse :
à l’instant t dans un référentiel R est égal à la dérivée par rapport au temps
du vecteur position
-
|
-
Remarque :
-
Notation simplifiée :

-
En conséquence, le vecteur
vitesse décrit les variations du vecteur position.
-
Sa direction est donnée par la
tangente à la courbe au point considéré.
-
Il dépend du référentiel d’étude.
e)-
Coordonnées du vecteur vitesse.
- Pour connaître les coordonnées du
vecteur vitesse, on dérive le vecteur position par rapport au
temps :
|
|
|
|
|
Vecteur
position |
par dérivation par rapport
au temps |
Vecteur
vitesse |
|
|
|
-
Le vecteur accélération est un
vecteur qui rend compte des variations du vecteur vitesse.
-
Il traduit les variations du
vecteur vitesse.
-
Pour déterminer, de façon
expérimentale, la valeur de l’accélération au temps
t, on
calcule la variation
![]() du
vecteur vitesse pendant un intervalle de temps très court
encadrant l’instant considéré.
du
vecteur vitesse pendant un intervalle de temps très court
encadrant l’instant considéré.
-
Représentation du vecteur
accélération à l’instant t3 :
-

![]() Le tracé :
Le tracé :
Animation CabriJava (Tracé du vecteur
|
|
|
|
|
|
|
|
|
|
|
|
Définition
du vecteur accélération :
le vecteur dérivé par rapport au temps du vecteur vitesse du
point
M
à cet instant. -
On écrit : |
-
Notation simplifiée : 
-
Ou encore : 
c)-
Coordonnées du vecteur accélération.
-
Pour connaître les coordonnées du
vecteur accélération, on dérive les coordonnées du vecteur
vitesse par rapport au temps :
|
|
|
|
|
Comme |
|
Alors |
|
|
=> |
|
|
|
par dérivation
par rapport
au
temps |
|
-
Récapitulatif :
|
Vecteur position |
Vecteur vitesse |
Vecteur accélération |
|
|
|
|
-
On donne les équations
paramétriques horaires du mouvement d’un point
M
dans le repère :  ,
,

-
Donner l’expression des
coordonnées du vecteur vitesse et du vecteur accélération du
point mobile
M
dans le repère
R.
|
Vecteur position |
Vecteur vitesse |
Vecteur accélération |
|
|
|
|
-
Remarque :
-
La valeur de l’accélération est
reliée aux coordonnées du vecteur accélération
ax
et ay par la relation de Pythagore :
-
![]()
-
Les coordonnées et la valeur du
vecteur accélération dépendent du temps et dépendent comme le
vecteur vitesse du référentiel d’étude.
6)- Le
vecteur quantité de mouvement. (Étude expérimentale : propulsion
et quantité de mouvement)
-
Le vecteur quantité de mouvement
 d’un point matériel est
égal :
d’un point matériel est
égal :
-
Au produit de sa masse
m,
-
Par son vecteur vitesse 
|
|
|
|
que le vecteur vitesse
|
|
|
|
|
|
|
-
Remarque :
-
Le vecteur quantité de mouvement
a toujours la même direction et le même sens que le vecteur
vitesse, car la masse m est une grandeur positive.
1)- Le
mouvement rectiligne uniforme.
a)-
Définition :
|
Mouvement rectiligne uniforme :
d’un mouvement rectiligne uniforme si son vecteur vitesse a toujours même direction, même sens et même valeur. - Son vecteur vitesse est un vecteur constant au cours du
temps. |
b)-
Conséquences :
-
La trajectoire est une portion de
droite
-
La valeur de sa vitesse est
constante au cours du temps.
-
Le système parcourt des distances
égales pendant des durées égales.
-
La valeur de la vitesse
instantanée ne varie pas au cours du temps.
-
Le vecteur vitesse est
indépendant du temps : ![]()
-
Le vecteur position et le vecteur
vitesse ont, à chaque instant, même direction et même sens.
-
Comme

-
Le vecteur accélération est un
vecteur nul et la valeur de l’accélération est nulle.
c)-
Caractéristiques graphiques du mouvement
rectiligne uniforme.
|
|
Vecteur position |
Vecteur vitesse |
Vecteur accélération |
|
|
|
|
|
|
Équations Horaires |
x (t)
= v0x
. t +
x0 |
vx
(t) =
v0x |
ax
(t) =
0 |
2)- Les
mouvements rectilignes uniformément variés.
a)-
Définition :
|
Mouvement rectiligne uniformément
varié :
son
vecteur accélération a toujours la même direction,
le même sens
et la même valeur.
- Le vecteur accélération est un vecteur
constant au cours du temps : |
b)-
Conséquences :
-
La trajectoire est une portion
de droite
-
La valeur de l’accélération est
constante au cours du temps.
-
Le vecteur position, le vecteur
vitesse et le vecteur accélération ont même direction.
-
La valeur de la vitesse est une
fonction affine du temps : vx =
a
x0 .
t +
v0x
c)-
Caractéristiques graphiques du mouvement
rectiligne uniformément varié.
|
Chronophotographie
du mouvement |
|
|
Représentation graphique de la coordonnée x de la position en fonction du temps |
|
|
Représentation graphique de la coordonnée vx de la vitesse en fonction du temps |
|
|
Représentation graphique de l’accélération ax en fonction du temps |
- Les équations horaires :
|
|
Vecteur position |
Vecteur vitesse |
Vecteur
accélération |
|
|
|
|
|
|
Équations Horaires |
|
vx
(t) =
a0x
. t +
v0x |
ax
(t) =
a0x |
3)- Les
mouvements circulaires uniformes.
a)-
Définition :
|
Mouvement circulaire uniforme
:
si sa trajectoire
est une portion de cercle de
rayon
R et si la valeur de
sa vitesse v est
constante. |
b)-
Conséquences :
- Le vecteur accélération est alors
centripète et sa valeur a
est constante.
- 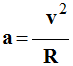
- Le mobile parcourt des arcs égaux
pendant des durées égales.
- Exemple :
|
Le mobile autoporteur, maintenu par un fil tendu, est lancé sur la table à digitaliser. La table est
horizontale. On enregistre la position du centre d’inertie du solide à intervalles de temps égaux t après
avoir lâché le mobile.
|
Animation CabriJava
-
Le vecteur vitesse est à chaque
instant perpendiculaire au vecteur accélération.
-
Le vecteur vitesse et le vecteur
accélération changent de direction à chaque instant.
-
Animation CabriJava.
4)- Les
mouvements circulaires non uniformes.
a)-
Exemple : Mouvement d’un pendule simple.
-
Un pendule simple est constitué
d’un objet sphérique de masse m suspendu à un fil
inextensible de longueur ℓ.
-
Remarque : la masse du fil est
négligeable devant celle de l’objet.
-
La longueur
ℓ est grande
devant celle de l’objet.
-
Dans le cas contraire, on dit que
le pendule est pesant.
-
On écarte le solide de sa
position d’équilibre d’un angle θ0 < 10°.
-
On laisse le pendule osciller
librement et on fait une représentation à un temps
t quelconque.
b)-
Définition :
-
Dans un référentiel donné, un
système est animé d’un mouvement circulaire non uniforme,
-
Si sa trajectoire est une portion
de cercle de rayon R
-
Et si la valeur de l’accélération n’est pas constante.
-
À chaque instant, le vecteur
accélération
![]() se décompose en deux
vecteurs :
se décompose en deux
vecteurs :
-
![]()
|
Vecteur accélération |
|
Le vecteur accélération
tangentielle |
Le vecteur accélération normale |
|
|
|
|
|
|
Direction |
Tangent à la trajectoire au point considéré |
Centripète |
|
|
Sens |
Orienté dans le sens du mouvement |
Orienté vers le centre du cercle |
|
|
Valeur |
C’est la dérivée par rapport au temps de la valeur de la vitesse
v |
|
5)- Cas
des mouvements accélérés, retardés, uniformes.
-
Cas particuliers importants : le
mouvement rectiligne uniforme, le mouvement rectiligne varié, le
mouvement circulaire uniforme.
► Quelles sont les caractéristiques
du vecteur accélération de ces mouvements ?
►
Que peut-on dire de
l'accélération tangentielle et de l'accélération normale ?
-
Si v ↑ au cours du
mouvement, celui-ci est accéléré.
-
Si v
↓ au cours du
mouvement, celui-ci est retardé.
-
Si v = cte le mouvement
est uniforme.
-
Remarque :
-
Le produit scalaire
![]() permet de
connaître si un mouvement est retardé ou accéléré.
permet de
connaître si un mouvement est retardé ou accéléré.
-

-
Si

-
Si

-
Si

![]() Un
référentiel galiléen est un référentiel dans lequel les lois de
Newton sont vérifiées.
Un
référentiel galiléen est un référentiel dans lequel les lois de
Newton sont vérifiées.
-
Pour simplifier l’étude du
système, on choisit toujours un référentiel adapté.
► Le référentiel terrestre ou
référentiel du laboratoire.
-
On utilise, le plus souvent,
comme repère lié au référentiel terrestre, deux axes horizontaux
et un axe vertical.
-
Ce référentiel est bien commode
pour l’étude du mouvement des objets dans une salle de classe,
pour tous les mouvements qui
s’effectuent au voisinage de la terre.
►
Le référentiel géocentrique.
-
L’origine du repère lié au
référentiel Géocentrique est située au centre de la Terre.
-
L’axe z’Oz est orienté
vers une étoile lointaine : on peut choisir l’étoile polaire.
-
Les axes
x’Ox et
y’Oy sont situés
dans le plan équatorial et ils sont orientés vers des étoiles
lointaines supposées fixes.
-
Ce référentiel est commode pour
l’étude des satellites de la Terre.
-
Ce référentiel n’est pas entraîné
dans le mouvement de rotation de la Terre.
-
Dans ce référentiel,
► Le référentiel Héliocentrique ou
de Copernic.
- L’origine du repère lié au référentiel Héliocentrique est située au centre du Soleil.
- Les
axes z’Oz,
x’Ox et
y’Oy sont orthogonaux et
ils sont orientés vers des étoiles lointaines supposées fixes.
-
Ce référentiel est commode pour
l’étude des satellites du Soleil.
-
Dans ce référentiel,
► Pour ces mouvements, ces
référentiels peuvent être considérés comme galiléens.
2)-
Première loi de Newton : le principe de l’Inertie.
|
Principe de l'Inertie
:
ou s’il est soumis à un ensemble de forces dont les effets se compensent (système pseudo-isolé),
alors il
est immobile ou
animé d’un mouvement rectiligne uniforme. |
-
Lorsqu’un système est isolé ou
pseudo-isolé :
-
Sa vitesse est constante, sa
quantité de mouvement est constant, on dit qu’elle se conserve.
-
![]()
3)-
Deuxième loi de Newton : Principe fondamental de la dynamique.
a)-
Énoncé :
|
Principe fondamental de la
dynamique :
une ou plusieurs forces extérieures, alors la somme vectorielle de ces forces est égale
à la dérivée par rapport au temps de son
vecteur quantité de mouvement : -
On écrit : |
b)-
Cas particulier : la masse du système se
conserve au cours du mouvement :
m = cte
-

c)-
Autre expression de la deuxième loi de
Newton.
-
Considérons le repère lié au
référentiel d’étude : 
-
Dans ce repère :
|
|
Coordonnées des
vecteurs |
Expression |
|
Résultante des forces extérieures
|
|
|
|
Vecteur quantité de mouvement
|
|
|
|
Deuxième loi de
Newton |
|
|
-
Remarque :
Fx
et Fy sont les coordonnées de la somme des
forces extérieures qui s’exercent sur le système.
d)-
Exemple : Cas du pendule simple.
-
Le système
S étudié : La
bille de masse m et de centre de gravité
G.
|
|
Coordonnées des
vecteurs |
|
Résultante des forces extérieures
|
|
|
Vecteur quantité de mouvement
|
|
|
Deuxième loi de
Newton
|
|
4)-
Troisième loi de Newton : Principe des actions réciproques.
a)-
Énoncé :
|
Principe des actions
réciproques :
-
A
est situé au point
O
et
B
est situé au point
P. -
Lorsqu’un corps
A
exerce sur un corps
B
une action mécanique représentée par le vecteur force
-
Le corps
B
exerce sur un corps
A
une action mécanique représentée par le vecteur force
-
Les forces
|
-
Schéma :

-
Remarque : Cette propriété est
toujours vraie, que les corps soient au repos ou en mouvement.
-
Schéma de l’interaction
Terre–Lune.

b)-
Mesure de la valeur du poids d'un corps
à l'aide d'un dynamomètre.
-
Le dynamomètre mesure aussi bien
la force qu'il exerce que la force qu'on lui applique.
-
Représentation schématique :
-
D'après les conditions
d'équilibre, on peut écrire que :
-
![]()
-
Et que les deux forces ont la
même droite d'action : P =
F2→1.
-
Le dynamomètre est en équilibre
et on considère qu'il a une masse négligeable.
-
On peut écrire que :
-
![]()
-
Et les deux forces ont la même
droite d'action : F2→1 =
F3→2.
-
D'après le principe de
d'interaction : F2→1 =
F1→2.
-
En conséquence :
F2→1 =
F1→2 =
P
-
Le dynamomètre mesure bien le
poids de l'objet ceci lorsque le dynamomètre est immobile.
► Que se passe-t-il si l’objet est
en mouvement ? Si le dynamomètre bouge ?
-
Si le dynamomètre bouge cela
n'est plus vrai : F2→1 =
F1→2
≠ P
-
Remarque :
-
La troisième loi de Newton est
vérifiée que les forces soient de contact ou à distance et que
les solides soient immobiles ou en mouvement.
c)-
Application : Interaction de contact et
propulsion.
Pourquoi pouvons-nous
marcher ?
► Schématiser un personnage qui se
déplace en marchant. Quelles sont les actions mécaniques qui
s’exercent sur le marcheur ?
-
Il y a l’action du sol sur le
marcheur
![]() et l’action de
la Terre sur le marcheur
et l’action de
la Terre sur le marcheur
![]() .
.
► Représenter par des vecteurs
forces l’action du sol sur ses pieds.

-
On peut décomposer la force
exercée par le sol sur le pied du marcheur par deux actions :
-
La réaction normale au support
qui empêche le pied de traverser le son ou de s’enfoncer dans le
sol et la réaction tangentielle qui empêche le pied de glisser
en arrière.

5)-
Application à la propulsion par réaction.
-
Dans un référentiel galiléen,
lorsqu’un système S assimilé à un point matériel est
soumis à des forces dont les effets se compensent :
-
D’après la deuxième loi de
Newton, on peut écrire :
-

-
Le vecteur quantité de mouvement
du système S = {m,
G} se conserve.
-
Le système
S est assimilé
à un point matériel G de masse
m.
-
Notation :
S
= {m,
G}
-
Si le système
S est
immobile, alors ![]()
-
Si ce système
S = {m,
G} se sépare en deux parties
S1
= {m1,
G1} et
S2
= {m2,
G2}
-
Les deux parties
S1
et S2 sont en interactions.
-
De plus : 
-
Les quantités de mouvement des
deux parties sont opposées puisque leur somme vectorielle est
nulle.
-
La conservation de la quantité de
mouvement permet d’expliquer la propulsion par réaction.
-
Exemple :
(à finir)
1)- QCM :
reconnaître un mouvement.
2)-
Exercices :
a)-
Exercice 7 page 146 : Choisir un
référentiel d’étude.
b)-
Exercice 10 page 146 : Connaître les
propriétés du vecteur accélération.
c)-
Exercice 11 page 147 : Représenter des
vecteurs vitesses.
d)-
Exercice 12 page 147 : Représenter des
vecteurs accélérations.
e)-
Exercice 16 page 148 : Analyser un
mouvement.
f)-
Exercice 18 page 148 : Déterminer des
forces inconnues.
g)-
Exercice 28 page 150 : Voiture au banc
d’essai.
h)-
Exercice 30 page 150-151 : Décollage
d’Ariane 5.
i)-
Exercice 34 page 152 : En impesanteur.
j)-
Exercice 35 page 153 : Le dauphin à
flancs blancs.
|
|

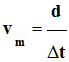

















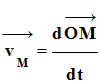















.gif)






















