|
|
Transferts thermiques Exercices |
|
|
|
|
|
QCM r
Transferts thermiques Le transfert thermique La température terrestre moyenne La loi de Newton |
1)- Exercice 02 page 334 : Identifier un transfert thermique :
|
Identifier un transfert thermique : Un jour d’été très chaud, la température de l’eau du lac de Lacanau en Gironde est 23 ° C, la température de l’air 30 ° C et celle du
sable 25 ° C. 1. Identifier le mode de transfert thermique
principal entre l’eau et le Soleil, l’eau et le sable, l’eau et
l’air. 2. Indiquer le sens de ces transferts et leur
signe si le système étudié est l’eau du lac.
|
|
Identifier un transfert thermique : 1. Identification du mode de transfert
thermique principal :
-
Entre l’eau et le Soleil : le
rayonnement thermique WR
-
Entre l’eau et le sable : la
conduction thermique Q1
-
Entre l’eau et l’air : la convection
thermique Q2 2.
Sens des transferts et leur signe si le
système étudié est l’eau du lac.
-
Le rayonnement thermique
WR se produit dans tout milieu et même dans le vide.
-
Le transfert thermique s’effectue du
corps chaud vers le corps froid.
|
2)- Exercice 04 page 334 : Déterminer un flux thermique :
|
Déterminer un flux thermique :
En été, un flux thermique Φ s’effectue à travers le
pare-brise séparant l’habitacle d’une voiture, de l’air extérieur. 1- Déterminer le sens du flux thermique Φ
traversant le pare-brise. 2- Calculer Φ.
- Données :
- Résistance thermique du verre du
pare-brise :
- Rth = 3,0 × 10–3
° C . W–1. - La résistance thermique Rth et le flux Φ orienté d’un point A vers
un point B sont liés
par :
-
|
|
Déterminer un flux thermique : 1- Sens du flux thermique Φ traversant
le pare-brise.
- Schéma :
- Le transfert thermique s’effectue du
corps chaud vers le corps froid.
- Il a lieu de l’extérieur de la
voiture vers l’intérieur de la voiture
- Le flux thermique est orienté de
l’extérieur (TA
= 40 ° C) vers l’intérieur (TB
= 22 ° C). 2- Calcul du flux thermique Φ.
- |
3)- Exercice 07 page 334 : Exploiter la loi de Stefan-Boltzmann :
|
Exploiter la loi de Stefan-Boltzmann : La photosphère est la surface visible du Soleil. Sa température
moyenne est 5778 K. Les taches solaires (sunspot) sont des zones de température plus
faible.
La puissance surfacique émise au niveau d’une des taches solaires
est voisine de : 1,18 × 107 W . m–2. 1.
Déterminer la puissance surfacique moyenne
émise par la photosphère considérée comme un corps noir. 2.
Calculer la température de surface au niveau
de la tache solaire évoquée.
-
Donnée :
-
La loi de Stefan-Boltzmann :
-
La puissance thermique surfacique
p émise par un
corps noir :
-
p = σ . T4
-
σ : Constante de
Stefan-Boltzmann ((W . m–2 . K–4)
-
σ = 5,67 ×10–8 W .
m–2 . K–4 |
Exploiter la loi de Stefan-Boltzmann : 1.
Puissance surfacique moyenne émise par la
photosphère.
-
La photosphère est considérée comme
un corps noir :
-
On peut utiliser la loi de
Stefan-Boltzmann :
-
p = σ . T4
-
p = 5,67 ×10–8 ×
(5778)4
-
p
≈ 6,319
× 107 W . m–2
-
p
≈ 6,32 × 107
W . m–2 2.
Température Tt de surface
au niveau de la tache solaire.
-
On considère que la tache solaire se
comporte comme un corps noir :
-
pt = 1,18 × 107
W . m–2
-
-
À la calculatrice :
-
(1.18E7/5.67E–8)^(1/4)
ENTER : 3.79817E3
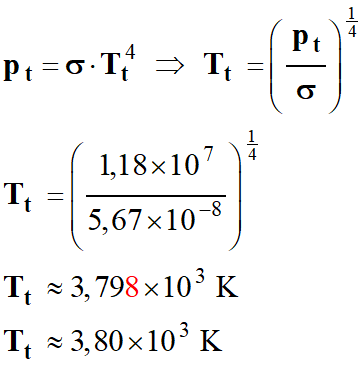
![]()
4)- Exercice 08 page 335 : Discuter de l’influence de l’Albédo :
|
Discuter de l’influence de l’Albédo :
-
Compléter les affirmations suivantes
avec certains termes ci-dessous :
-
Absorbé(e) ; 70 % ;
inférieur(e) ; 30 % ;
supérieur(e) ;
renvoyé(e). a.
L’albédo est le pourcentage de la puissance
solaire qui est ………. par le système {Terre et atmosphère} b.
L’albédo de la glace est ………. à celui des
forêts. c.
Sans albédo, la température terrestre
moyenne serait ………. à celle avec l’albédo. |
Discuter de l’influence de l’Albédo : a.
L’albédo est le pourcentage de la puissance
solaire qui est renvoyé par le système {Terre et atmosphère}
-
L’albédo
α est une grandeur sans
unité qui caractérise l’aptitude d’une surface à renvoyer,
par
diffusion et / ou réflexion, le rayonnement qui lui parvient. b.
L’albédo de la glace est supérieur à
celui des forêts
-
(Pour la glace 0,5 <
α < 0,7 pour les forêts : α ≈ 0,1) c.
Sans albédo, la température terrestre
moyenne serait supérieure à celle avec l’albédo.
-
L’albédo et l’effet de serre exercent
une grande influence sur la température moyenne de la Terre
-
Tableau :
TT
(° C)
Sans
Albédo et sans effet de serre
5
Avec
Albédo et sans effet de serre
–18
Avec
Albédo et avec effet de serre
15
-
Une diminution de l’Albédo du système
{Terre et atmosphère} entraîne une élévation de la température
moyenne de la Terre.
![]()
5)- Exercice 11 page 335 : Exploiter la loi de Newton :
|
Exploiter la loi de Newton : La paroi d’un système incompressible à la température T = 323 K est mise en contact avec un fluide à la température constante
Te = 293 K. On suppose ici que le coefficient d’échange convectif h du fluide est : h = 10 W . m–2 . K–1.
-
Calculer le flux convectif
Φ entre le système et l’extérieur à travers la paroi dont la surface S = 1,0
m2.
-
Donnée :
-
Loi de Newton :
-
Φ = h . S . (Te
– T) |
|
Exploiter la loi de Newton :
-
Flux convectif
Φ entre le système et l’extérieur à travers la paroi
-
h = 10 W . m–2
. K–1
-
S = 1,0 m2
-
Loi de Newton :
-
Φ = h . S . (Te
– T)
-
Φ = 10 × 1,0 × (293 – 323)
-
Φ ≈ – 3,0 × 102 W
-
Φ < 0
-
Le système cède de l’énergie au
milieu extérieur.
-
Schéma :
|
6)- Exercice 12 page 335 : Effectuer un bilan d’énergie :
|
Effectuer un bilan d’énergie : 1. À partir de la loi de Newton, exprimer le transfert thermique Q effectué par convection entre un système incompressible à la température θ et le milieu extérieur à la température θe (ou thermostat) pendant la durée Δt. Le système ou le milieu
extérieur est fluide. 2.
Exprimer Q en fonction de la masse
m du système, de sa capacité thermique massique c et de la
variation de température Δθ. 3.
Déduire des relations précédentes l’équation
différentielle vérifié par la température θ.
-
Donnée :
-
Donnée :
-
Loi de Newton :
-
Φ = h . S . (θe
– θ) |
|
Effectuer un bilan d’énergie : 1. Expression du transfert thermique Q effectué par convection entre un système
incompressible à la température θ et le milieu extérieur à la
température θe (ou thermostat) pendant la durée
Δt.
-
Loi de Newton :
-
Φ = h . S . (θe
– θ)
-
Le système ou le milieu extérieur est
fluide :
-
Sur une durée Δt suffisamment courte, on peut considérer que le flux thermique
Φ est constant.
-
Q = Φ .
Δt
-
Q = h . S .
(θe –
θ) .
Δt (1) 2.
Expression de Q en fonction de la
masse m du système, de sa capacité thermique massique c
et de la variation de température Δθ.
-
Q =
m .
c . Δθ (2) 3.
Équation différentielle vérifié par la
température θ.
-
En combinant les relations (1) et
(2) :
-
m .
c .
Δθ = h . S . (θe
– θ) .
Δt
►
Établissement de l’équation
différentielle :
-
Lorsque Δt → 0, - La limite de l’expression -
On écrit en utilisant la notation
différentielle : -
-
En développant, on obtient : - -
Et enfin : -
|
7)- Exercice 14 page 335 : Résoudre une équation différentielle :
|
Résoudre une équation différentielle : À la sortie d’un four, un gâteau dans son moule est à la température θi = 180 ° C. Le système {gâteau et moule} est laissé à la température ambiante
constante θe = 20 ° C. L’équation différentielle vérifiée par la température du système
est :
-
Dans cette relation, a est une constante négative qui dépend du
système et du fluide étudié. 1.
Montrer, en résolvant l’équation
différentielle, que 2.
Quelle sera la température du gâteau une
heure après la sortie du four ?
-
Données :
-
On considère que le système {gâteau
et moule} est un système incompressible. - On néglige les échanges de matière entre le système et le milieu extérieur : Le seul transfert
thermique est convectif.
-
Dans la situation étudiée :
a = – 3,8 × 10–4
s–1 |
|
Résoudre une équation
différentielle : 1.
Solution de
l’équation différentielle
-
Système
d’étude : {gâteau et moule}
-
θi
= 180 ° C.
-
Température du milieu extérieur :
θe = 20 ° C
-
L’équation
différentielle vérifiée par la température du système est :
-
-
On
considère que le système {gâteau et moule} est un système
incompressible. - On néglige les échanges de matière entre le système et le milieu extérieur : Le
seul transfert thermique est convectif.
-
Dans la
situation étudiée : a = –
3,8 × 10–4 s–1
-
Vérification :
-
Détermination de :
-
-
-
La
solution
-
D’autre
part :
-
Au temps t
= 0, θ (0) =
θi 2.
Température θ1
du gâteau une heure après la sortie du four
-
-
Évolution
de la température du système au cours du temps :
-
Le temps
caractéristique τ :
-
-
Détermination graphique :
-
On trace
la tangente à la courbe au point d'abscisse
t = 0 s et l'asymptote
horizontale
-
La
constante de temps τ est donnée par l'abscisse de leur point
d'intersection.
-
On peut
considérer que le gâteau est à la température ambiante (20 ° C) au
bout de la durée de 5 τ, c’est-à-dire de 3,5 h environ.
|
8)- Exercice 15 page 336 : Un biberon à la bonne température :
|
Un biberon à la bonne température :
« on chauffe un biberon sorti du réfrigérateur en moins de trois minutes. Le lait est constamment mélangé pendant
qu’il chauffe, afin d’éviter la formation de points chaud. » On étudie le transfert thermique convectif Q entre le lait
et un chauffe-biberon maintenant les parois du biberon à la
température constante θe = 50 ° C. 1. À l’aide de la loi de Newton, exprimer le transfert thermique Q effectué par convection entre le système {lait} et le milieu extérieur constituant un thermostat, pendant la durée Δt. 2.
Donner l’expression de Q en fonction
de la masse m du système, de sa capacité thermique massique
c et de sa variation de température Δθ. 3.
Déduire des relations précédentes l’équation
différentielle vérifiée par la température du lait. 4.
Montrer que l’expression
5.
Un biberon contenant du lait à la
température θi = 5 ° C est placé dans le
chauffe-biberon. a.
Au bout de quelle durée peut-il être donné à
la température de 30 ° C au nourrisson ? b.
La durée obtenue est-elle conforme aux
données du fabricant ?
-
Données :
-
On néglige tout transfert thermique
autre que convectif entre le système et le milieu extérieur.
-
Surface d’échange du lait dans le
biberon : S = 270 cm2.
-
Coefficient d’échange convectif du
lait dans les conditions de l’utilisation du chauffe-biberon :
-
h = 300 W m–2
. °C–1.
-
Capacité thermique massique du lait :
-
c = 4,2 × 103 J . kg–1
. °C–1.
-
Masse du lait dans le biberon :
-
m = 350 g
-
loi de Newton :
-
Φ = h . S . (θe
– θ) |
Un biberon à la bonne température : 1.
Transfert thermique Q effectué par
convection entre le système {lait} et le milieu extérieur pendant la
durée Δt.
-
À l’aide de la loi de Newton : Φ
= h . S . (θe – θ)
-
Q = Φ
. Δt
-
On suppose que pendant la durée
suffisamment courte Δt le
flux thermique Φ est constant.
-
Q = h . S .
(θe – θ)
. Δt (1) 2.
Expression de Q en fonction de la
masse m du système, de sa capacité thermique massique c
et de sa variation de température Δθ.
-
Q = m
. c
.
Δθ (2) 3.
Équation différentielle vérifiée par la
température du lait.
-
Le système
S :
-
Il est incompressible et il est à la
température θ au temps t ;
-
Il échange de l’énergie par
transfert thermique convectif avec le thermostat
-
Il est en contact avec le milieu
extérieur, ou thermostat à la température constante
θe.
-
Il n’échange pas de matière avec le
milieu extérieur ou thermostat.
-
On note
θi la
température du système S
à l’instant initial.
►
Application du premier principe de la
thermodynamique au système S :
-
Il n’échange pas de travail
W avec le milieu extérieur.
-
Il échange seulement de l’énergie
Q par transfert thermique
convectif avec le thermostat (milieu extérieur).
-
Entre l’état initial (i) et l’état final (f),
on peut écrire :
-
ΔUi→f =
Q
-
Pour une durée suffisamment courte,
on peut écrire :
-
Q =
Φ .
Δt
-
D’après la loi de Newton :
-
Φ =
h .
S . (θe –
θ)
-
Q =
h .
S . (θe –
θ) .
Δt
-
D’autre part, pour un système
incompressible de masse m, de capacité thermique massique
c dont la variation de température est Δθ :
-
Q =
m .
c . Δθ
-
On obtient la relation suivante :
-
ΔUi→f =
h .
S . (θe –
θ) .
Δt = m .
c . Δθ
-
On peut exprimer le rapport de
l’écart de température Δθ
sur la durée Δt :
-
►
Établissement de l’équation
différentielle :
-
Lorsque
Δt → 0,
-
La limite de l’expression
-
On écrit en utilisant la notation
différentielle :
-
4.
Solution de l’équation différentielle.
-
Comme :
-
L’équation différentielle devient :
-
-
La solution :
-
Elle vérifie l’équation
différentielle (1)
-
On détermine l’expression de
-
-
On remplace
-
-
L’égalité est bien vérifiée.
-
L’expression
5.
Un biberon contenant du lait. a.
Durée au bout de laquelle la température est
de 30 ° C
-
Température initiale : θi =
5 ° C
-
Température finale θe
= 30 ° C
-
Valeur de la constante
a :
-
-
-
Application numérique :
-
b.
Conformité du produit :
-
Le produit est conforme aux
indications de la notice :
-
t ≈ 2,5 min
-
« on chauffe un biberon sorti du
réfrigérateur en moins de trois minutes. … »
-
Évolution de la température θ
du système au cours du temps t :
-
Le temps caractéristique
τ :
-
-
Détermination graphique :
-
On trace la tangente à la courbe au
point d'abscisse t = 0 s
et l'asymptote horizontale
-
La constante de temps τ est
donnée par l'abscisse de leur point d'intersection.
►
Détermination expérimentale de la
constante de temps τ.
-
Dans le cas présent : θi
= 5,0 ° C et θe = 50 ° C
-
![]()
![]() est égale à la dérivée de
θ par rapport au temps t :
est égale à la dérivée de
θ par rapport au temps t :![]() :
:![]()
![]()
![]() :
:![]() :
: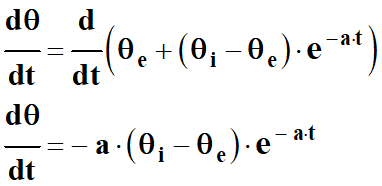
![]() et
θ par leur expression
respective dans l’équation différentielle (1)
et
θ par leur expression
respective dans l’équation différentielle (1)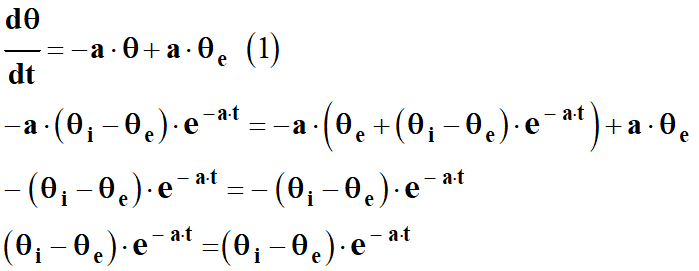
![]() est bien une solution de
l’équation différentielle (1).
est bien une solution de
l’équation différentielle (1).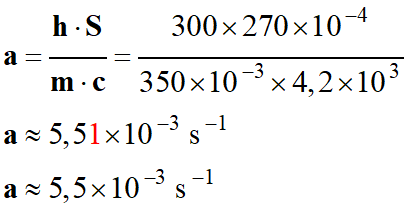
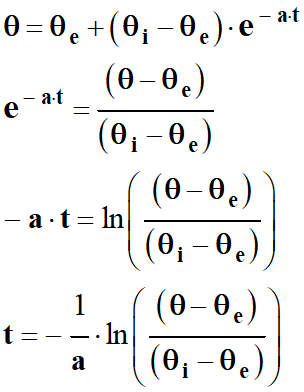
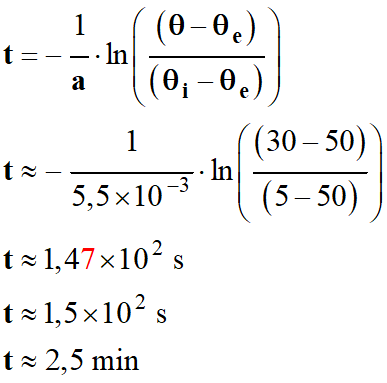
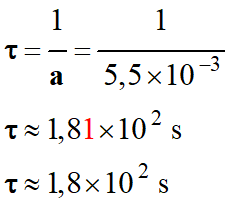
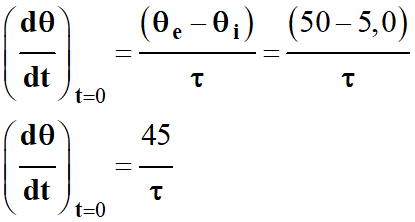
![]()
9)- Exercice 19 page 337 : Pertes thermiques :
|
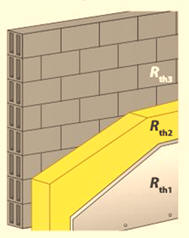
Pertes thermiques :
Un mur est constitué d’une cloison de plâtre de résistance thermique Rth1 collée à une couche de laine de verre de résistance thermique Rth2. L’ensemble est
fixé à une paroi de béton de résistance Rth3. La surface du mur est S = 20 m2. La température
à l’intérieur de la pièce est θi = 20 ° C ; celle
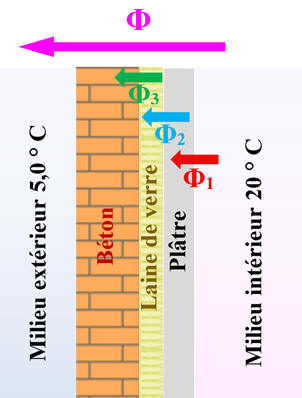
du milieu l’extérieur est θe = 5,0 ° C. 1.
Schématiser la situation en indiquant par
une flèche le sens des transferts thermiques à travers le mur. 2.
Indiquer le mode transfert mis en jeu. 3.
Calculer la résistance totale Rth
du mur. 4.
Calculer le flux thermique Φ
traversant le mur. 5.
Comparer Φ avec le flux thermique
traversant une simple paroi de béton pour une même différence de
température.
-
Données :
-
Résistances thermiques en ° C . W–1
pour S = 20 m2.
-
La résistance totale d’un mur
constitué de couches accolées est égale à la somme des résistances
thermiques de chacune des couches. |
Pertes thermiques :
1.
Schéma de la situation.
-
Vue de profil : 2.
Mode transfert mis en jeu.
-
Le mode de transfert thermique à
travers les différentes parties du mur se fait par conduction. 3.
Résistance totale Rth du
mur.
-
Lorsque plusieurs parois sont
accolées, la résistance thermique totale Rth tot
est égale
à la somme des résistances thermiques de chaque paroi.
-
Relation :
-
-
Avec : Rth tot =
Rth1 + Rth2 + Rth3
+ Rth4 + …
-
Dans le cas présent avec les
notations de l’énoncé :
-
Rth = Rth1
+ Rth2 + Rth3
-
Rth =
0,039 + 0,125 + 0,013
-
Rth ≈ 0,177 ° C . W–1
-
Plus la résistance thermique du
matériau est élevée, plus le flux thermique est faible à travers le
matériau. 4.
Flux thermique Φ traversant le mur.
-
5.
Comparaison de Φ avec le flux
thermique traversant une simple paroi de béton.
-
Flux thermique transversant un mur de
béton dans les mêmes conditions.
-
-
Le mur de béton est nettement moins
isolant que le mur avec isolation.
-
Les pertes thermiques sont très
importantes dans le cas d’un seul mur de béton.
-
Φb >>
ΦbLp
-
Les pertes thermiques sont plus de 13
fois plus importantes dans le cas d’un seul mur de béton par rapport
à un mur isolé.
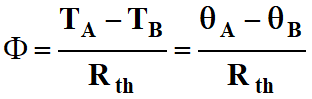
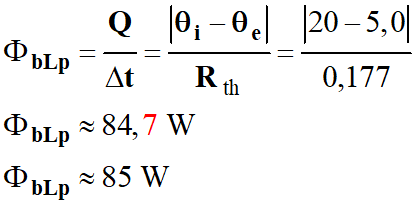
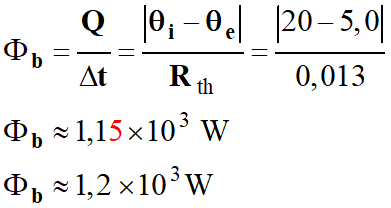
![]()
10)- Exercice 23 page 338 : Température des planètes du système solaire :
|
Température des planètes du système solaire : Différents facteurs influent sur la température de surface d’une
planète :
-
La puissance solaire surfacique
reçue ;
-
La présence ou non d’une atmosphère ;
-
L’albédo de la planète ;
-
La nature des gaz présents dans
l’atmosphère. A.
Quelques caractéristiques de quatre
planètes :
-
Tableau
A :
B.
Puissance surfacique p’S à
une distance D entre la planète et le Soleil
-
-
Puissance surfacique émise par la
Soleil à sa surface :
-
pS = 6,32 × 107
W . m–2.
-
Le rayon solaire :
-
RS = 6,96 × 108
m 1.
Calculer p’S pour chacune
des planètes du tableau. 2.
Justifier que la puissance solaire incidente
surfacique pP reçue en moyenne par le système
{planète et atmosphère} s’écrit :
3.
Évaluer la puissance solaire surfacique
moyenne absorbée pP(abs) par chaque planète. 4. On considère que les planètes réémettent intégralement la puissance qu’elles ont absorbée. Calculer la
température de surface des quatre planètes considérées comme des
corps noirs. 5.
Comparer les résultats à ceux du tableau
A et proposer une explication aux différences observées.
-
Données :
-
Loi de Stefan-Boltzmann :
-
Puissance surfacique émise par un
corps noir :
-
p = σ . T4
-
Constante de Stefan-Boltzmann :
-
σ = 5,67 ×10–8 W .
m–2 . K–4
-
T : Température du corps noir
en kelvin (K ).
-
Conversion de température : T (K) =
θ (° C) + 273. |
|
Température des planètes du système solaire : 1.
Puissance surfacique reçue du Soleil p’S
pour chacune des planètes du tableau.
-
Données :
-
-
Puissance surfacique émise par la
Soleil à sa surface :
-
pS = 6,32 × 107
W . m–2.
-
Le rayon solaire :
-
RS = 6,96 × 108
m
-
Calcul pour Mercure :
-
-
Tableau :
2.
Justification de la relation :
-
Schéma :
-
Comme le Soleil est très éloigné de
la planète, on considère que les rayons lumineux provenant du Soleil
sont parallèles.
-
Puissance solaire incidente
surfacique pP reçue en moyenne par le système
{planète et atmosphère} :
-
On considère que la planète se
comporte comme un disque de surface
SD et de rayon
RP.
-
Ce disque reçoit la puissance
suivante de la part du Soleil :
-
-
-
La planète tourne sur elle-même.
-
La puissance
-
Comme on considère que la planète est
sphérique, c’est la surface d’une sphère.
-
SP = 4 .
π . RP2
-
Pour connaître la puissance
surfacique reçue du Soleil par la planète, il suffit de diviser la
puissance
-
3.
Évaluation de la puissance solaire
surfacique moyenne absorbée pP(abs) par chaque
planète.
-
On connait l’Albédo pour chaque
planète.
-
L’Albédo est le pouvoir réfléchissant
d’une surface.
-
L’albédo
α est une grandeur sans
unité qui caractérise l’aptitude d’une surface à renvoyer, par
diffusion et / ou réflexion, le rayonnement qui lui parvient.
-
Sa valeur est comprise entre 0 et 1.
-
Exemple :
-
Relation :
-
La puissance solaire surfacique
moyenne absorbée pP(abs) :
-
pP(abs) = p’S
– |pR|
-
pP(abs) = p’S
– α . p’S
-
pP(abs) = (1
– α) . p’S
-
Tableau :
4.
Température
de surface des quatre planètes considérées comme des corps noirs.
-
Un corps noir est un objet théorique
qui absorbe intégralement le rayonnement électromagnétique qu’il
reçoit.
-
La loi de Stefan-Boltzmann permet de
relier cette température T
(K) au flux thermique surfacique rayonné
φE ou à la
puissance thermique surfacique
p.
-
Remarque :
p est comptée ici positivement.
-
Dans le cas présent, on peut écrire
que :
-
pP(abs) = σ
. T4
-
-
Calcul pour la Terre :
-
-
θ (° C) =
T (K)
– 273
-
θ (° C) ≈ – 18 ° C
-
Tableau :
5.
Comparaison des résultats à ceux du tableau
A.
-
On remarque que les écarts sont
importants pour Vénus et la Terre car ces planètes possèdent une
atmosphère qui contient des gaz à effet de serre.
►
Cas de la Terre :
-
Une augmentation de l’effet de serre
entraîne une augmentation de la température terrestre moyenne.
-
Schéma : - L’effet de serre est dû aux gaz de l’atmosphère (principalement l’eau et le dioxyde de carbone) qui absorbent
et renvoient vers la Terre une partie des radiations infrarouges qu’elle émet. - Un gaz à effet de serre est un gaz qui absorbe une partie du rayonnement infrarouge provenant de la Terre
et qui en réémet ensuite une partie vers la Terre et contribue ainsi à son réchauffement.
►
Cas de Vénus :
-
L’atmosphère de Vénus est constituée
de 96,5 % de dioxyde de carbone et de 3,5 % de diazote.
-
D’autres gaz sont présents mais en
très faibles proportions ( H2,
O2,
H2S, …)
-
De la vapeur d’eau (H2O) a été
détecté mais en très faible quantité.
-
Vénus et la Terre ont des tailles et
des masses comparables.
-
Toutefois, la planète Vénus est plus
proche du Soleil que la Terre.
-
Vénus reçoit environ deux fois plus
d’énergie solaire que la Terre.
-
Pourtant ce n’est pas pour cette
raison que la température moyenne de surface de Vénus (470 ° C) est
plus élevée que celle de la Terre (15 ° C) . - Cette différence est surtout liée à la présence de dioxyde de carbone (gaz à effet de serre) dans l’atmosphère de Vénus (96,5 %),
alors que la proportion de dioxyde
de carbone dans l’air est de l’ordre de 0,04 %. |
|
|