|
|
Mouvement et deuxième loi de Newton Exercices |
|
|
|
|
|
QCM r
Les vecteurs
position, vitesse et accélération Des exemples de
mouvements La deuxième loi de Newton |
1)- Exercice 04 page 228 : Déterminer les coordonnées d’un vecteur accélération :
|
Déterminer les coordonnées d’un vecteur accélération : Une bille assimilée à un point B est lancée verticalement
à un instant t = 0 s. Ses positions sont repérées dans un repère
avec x
et y en mètre (m) et t en secondes (s). Établir l’expression des coordonnées cartésiennes du vecteur vitesse, puis du vecteur accélération de la bille B. |
|
Déterminer les coordonnées d’un vecteur accélération : Une bille assimilée à un point B est lancée verticalement
à un instant t = 0 s. Le référentiel terrestre :
►
Les coordonnées cartésiennes du
vecteur position de la balle B :
►
Les coordonnées cartésiennes du
vecteur vitesse de la balle B :
-
Le vecteur vitesse d’un point mobile
M : - Dans un référentiel R donné, le vecteur vitesse, d’un point M à l’instant t,
est égal à la dérivée, par
rapport au temps, du vecteur position
à cet instant :
-
Dans le cas présent :
►
Les coordonnées cartésiennes du
vecteur accélération de la balle B : - Dans un référentiel R donné, le vecteur accélération d’un point M à l’instant t, est égal à la dérivée , par
rapport au temps, du vecteur vitesse
à cet instant :
-
Dans le cas présent :
-
Récapitulatif :
|
2)- Exercice 06 page 228 : Étudier un mouvement circulaire :
|
Étudier un mouvement circulaire : Un point matériel M décrit un mouvement circulaire
uniforme autour d’un point O.
1.
Reproduire le schéma, puis définir le repère
de Frenet lié au point M. 2.
Exprimer les coordonnées du vecteur
accélération
|
|
Étudier un mouvement circulaire : 1.
Repère de Frenet lié au point M.
-
Pour simplifier l’étude d’un tel
mouvement et en déduire
les caractéristiques, il faut utiliser le repère de Frenet :
-
-
-
-
Schéma :
- Le vecteur vitesse est tangent à la trajectoire au point considéré :
-
-
Le vecteur vitesse change de
direction à chaque instant.
-
Coordonnées du vecteur vitesse dans
le repère de Frenet :
-
2.
Coordonnées du vecteur accélération
-
Pour obtenir les coordonnées du
vecteur accélération,
il faut dériver l’expression
-
Le vecteur accélération peut se
décomposer de la façon suivante :
-
-
En conséquence, le vecteur
accélération peut être décomposé en une :
-
Accélération tangentielle
-
-
Accélération normale
-
-
Autre expression du vecteur
accélération :
-
-
-
Dans ce cas
-
Le vecteur accélération
-
-
Le mobile parcourt des arcs égaux
pendant des durées égales.
-
-
|
3)- Exercice 08 Page 229 : Exploiter les caractéristiques du vecteur accélération :
|
Exploiter les caractéristiques du vecteur accélération.
-
Relier chacun des pointages suivants
aux caractéristiques du vecteur accélération
|
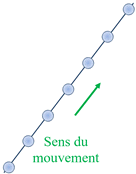
Exploiter les caractéristiques du vecteur accélération.
-
Caractéristiques du vecteur
accélération
Mouvement rectiligne
uniforme : Le
mobile parcourt des
distances égales pendant
des durées égales :
v
= cte
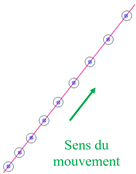
Mouvement rectiligne
accéléré : Le
mobile parcourt des
distances de plus en plus
grandes pendant
des durées égales
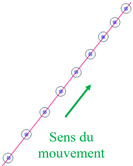
Mouvement rectiligne
retardé : Le
mobile parcourt des
distances de plus en plus
petites pendant
des durées égales
![]() de chaque enregistrement:
de chaque enregistrement:
![]()


![]()
4)- Exercice 10 page 229 :Tracer la trajectoire du centre de masse d’un système :
|
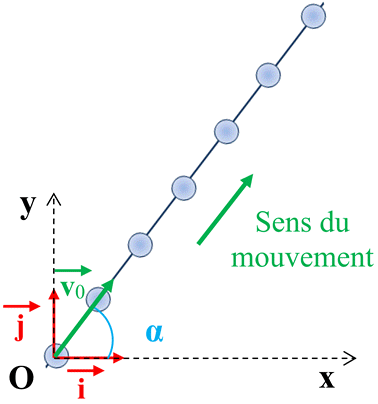
Tracer la trajectoire du centre de masse
d’un système : Un mobile autoporteur est lancé sur une table horizontale dans un référentiel terrestre considéré comme galiléen. On néglige les force de
frottement.
-
Représenter la trajectoire du centre
de masse G de ce mobile. |
Tracer la trajectoire du centre de masse
d’un système :
-
Trajectoire du centre de masse
G de ce mobile
-
Système :
S = (m,
G)
-
Référentiel d’étude : La table plane
et horizontale :
-
Référentiel terrestre supposé
galiléen :
-
Bilan des forces :
-
Comme les forces de frottement sont
négligeables
-
Le mobile est soumis à :
-
son poids
-
la réaction du support
-
avec
-
Schéma du mobile à l’instant t :
-
La deuxième loi de Newton appliquée
au système S, dans le
référentiel galiléen permet d’écrire :
-
Énoncé :
-
Dans un référentiel galiléen, la
somme des vecteurs forces
de masse m et de centre de masse G,
est égal au produit de sa masse
m par le vecteur accélération
Valeur des forces F en newton (N)
Valeur de la masse m en kilogramme (kg)
Valeur de l’accélération aG en mètre
par seconde au carré (m . s–2)
-
Dans le cas présent :
-
-
Le mobile se déplace dans le plan
horizontal :
-
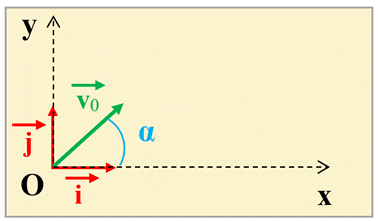
Conditions initiales :
-
On lance le mobile à l’instant
t = 0, du point
O avec une vitesse
-
Vecteur position à l'instant initial :
-
-
Dans ce repère :
-
Coordonnées du vecteur accélération :
-
-
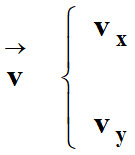
Coordonnées du vecteur vitesse :
-
-
On connaît
les coordonnées du vecteur accélération :
-
Or par définition :
-
-
La coordonnée
vx est une primitive de
ax :
-
La primitive est connue à une
constante près.
-
Cette constante que l'on note
vox est liée
aux conditions initiales.
-
Elle représente la composante de la
vitesse du mobile suivant l'axe
x'Ox au temps
t = 0.
-
En conséquence, les constantes qui
apparaissent sont liées aux conditions initiales et parfaitement connues à partir des conditions initiales
-
Comme
ax = 0, alors
vx = cte =
v0x
-
De même :
ay = 0, alors vy
= cte = v0y
-
-
Coordonnées du vecteur position :
-
-
La coordonnée
x est une primitive de
vx :
-
Comme
vx =
v0 . cos
α, alors x = (v0 . cos
α) .
t + x0
-
Avec
x0 = 0, =>
x = (v0 . cos α) .
t
-
De même :
-
La coordonnée y est une primitive de
vy :
-
Comme
vy =
v0 . sin
α, alors y = (v0 . sin
α) .
t + y0
-
Avec
y0 = 0, =>
y = (v0 . sin α) .
t
-
-
La trajectoire du mouvement du point
mobile G.
-
-
La trajectoire est du type :
y =
a . x
-
Le mouvement est rectiligne, la
trajectoire est une portion de droite.
-
D’autre part :
v = v0 = cte
-
Le mobile parcourt des distances
égales pendant des durées égales.
-
Le mouvement du centre de masse
G du mobile est
rectiligne uniforme.
-
Type d’enregistrement :

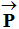 , force verticale orientée
du haut vers le bas.
, force verticale orientée
du haut vers le bas.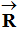 , force
verticale orientée du bas vers le haut
, force
verticale orientée du bas vers le haut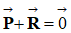

![]() appliquées à
un système S,
appliquées à
un système S, ![]() de son centre de masse.
de son centre de masse.
![]()
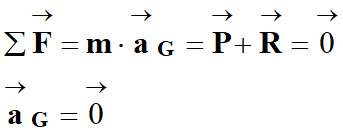


![]() faisant un angle
α avec l’axe (Ox) :
faisant un angle
α avec l’axe (Ox) :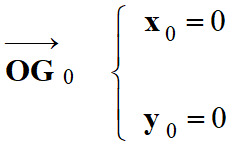 et vecteur vitesse initiale :
et vecteur vitesse initiale : 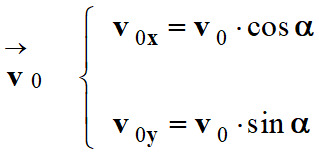
![]()
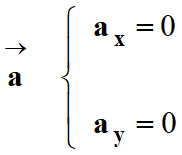
![]()
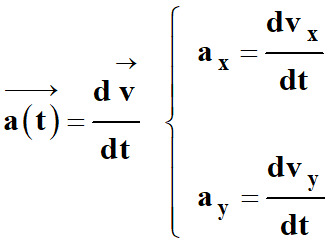
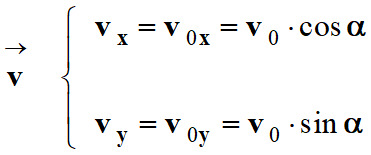
![]()
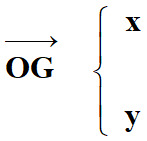
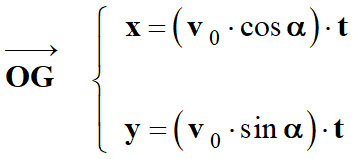
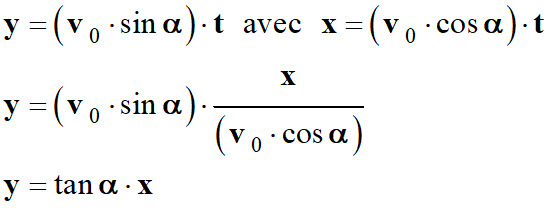
![]()
5)- Exercice 12 page 229 : Appliquer la deuxième loi de Newton :
|
Appliquer la deuxième loi de Newton : Une voiture de masse m = 900 kg se déplace moteur arrêté sur une route horizontale. Elle ralentit sous l’effet des forces de frottement exercées par l’air et par la route sur les pneus. Toutes les forces qui s’appliquent sur la voiture sont représentées en son centre de masse M sans souci d’échelle. Le poids
La valeur de la force de frottement f = 300 N.
|
|
Appliquer la deuxième loi de Newton :
-
Étude préliminaire :
-
Système :
S = (m,
M)
-
Référentiel d’étude : La route
-
Référentiel terrestre supposé
galiléen :
-
Bilan des forces :
-
les forces de frottement :
-
avec
f = 300 N (force
horizontale de sens opposé au mouvement)
-
le poids
-
la réaction du support
-
avec
1.
Énoncé de la deuxième loi de Newton.
-
Énoncé :
-
Dans le cas présent :
-
2.
Les caractéristiques du vecteur accélération
de M.
-
Coordonnées des différents vecteurs
dans le repère :
←
-
-
La deuxième loi de Newton appliquée à
la voiture dans le repère R :
-
-
Coordonnées du vecteur accélération :
-
-
Le vecteur accélération :
-
A même direction et même sens que le
vecteur
- (sens opposé à celui du mouvement)
-
Et pour valeur aM ≈ 0,333 m . s–2 |
6)- Exercice 16 page 230 : Virage d’un avion :
|
Virage d’un avion : On s’intéresse au mouvement du centre de masse G d’un avion de 50 tonnes qui entame un virage contenu dans le plan horizontal. Lors du virage, la
trajectoire de G est une portion de cercle de rayon R = 10 000 m, et sa vitesse a
une valeur constante v = 800 km . h–1.
1.
Déterminer la valeur aG de
l’accélération du centre de masse de l’avion au cours du virage. 2.
Déterminer la valeur Σ F de la somme
des forces qui s’appliquent sur l’avion dans cette situation. |
|
Virage d’un avion : 1.
Valeur aG de
l’accélération du centre de masse de l’avion au cours du virage. - Lors du virage, la trajectoire de G est une portion de cercle de rayon R = 10 000 m,
et sa vitesse a une valeur constante
v = 800 km . h–1
-
L’avion est animé d’un mouvement
circulaire uniforme :
-
Repère de Frenet :
-
-
-
Avion (vue de dessus) :
-
-
En conséquence, le vecteur
accélération peut être décomposé en une :
-
Accélération tangentielle
-
-
Accélération normale
-
-
Autre expression du vecteur
accélération :
- - Dans un référentiel donné, un système est animé d’un mouvement circulaire uniforme si sa trajectoire est une portion de cercle de rayon R et
si la valeur de sa
vitesse v est constante.
-
Comme
-
Dans le cas présent :
-
2.
Valeur Σ F de la somme des forces qui
s’appliquent sur l’avion dans cette situation.
-
Lorsqu’une aile d’avion est en
mouvement avec une vitesse
-
On appelle portance
-
Système : {Avion} = (m, G)
-
Référentiel terrestre supposé
galiléen :
►
Deuxième loi de Newton.
-
Énoncé :
-
Dans le cas présent :
-
-
Le vecteur
-
Sa valeur
Σ F :
-
-
Lors du mouvement circulaire
uniforme :
-
-
Le vecteur
-
Σ F = T ≈ 2,47
× 105 N |
7)- Exercice 17 page 230 : Saut au-dessus du canal de Corinthe :
|
Saut au-dessus du canal de Corinthe : En avril 2010, le pilote de moto Robbie MADDISON a pris son élan
pour franchir le canal de Corinthe. Le mouvement du centre de masse G du système {R. MADDISON et sa moto} est étudié dans un référentiel terrestre supposé galiléen. À l’instant t = 0 s, il se trouve à l’origine du repère et quitte le tremplin. Son vecteur vitesse
1.
Exploitation de la chronophotographie : a.
Utiliser la chronophotographie ci-dessous
pour montrer que le mouvement suivant l’axe (Ox) est uniforme. b.
Montrer que si le poids est la seule force
qui s’applique sur le système, le vecteur accélération est vertical. c.
Vérifier que les réponses aux deux questions
précédentes sont cohérentes entre elles. Un saut de 95 mètres () de haut et de 85 mètres de
long Canal de Corinthe : largeur 25 m, longueur
6,343 km Hauteur : 79 m 2.
Exploitation de la courbe vy
= f (t) : a.
En utilisant l’allure de la courbe
ci-dessous, justifier que le mouvement suivant l’axe vertical est uniformément varié. b. Quelle position particulière de la trajectoire est occupée par G à la date pour laquelle vy = 0 ? Quelle est alors la valeur de la
vitesse ?
-
Donnée : intensité de la pesanteur :
g = 9,82 N . kg–1
ou m . s–2 |
|
Saut au-dessus du canal de Corinthe :
-
Travail préparatoire :
-
Conditions initiales :
-
Système d’étude : {R. MADDISON et sa
moto} : S
= (m,
G)
-
Référentiel d’étude (terrestre
supposé galiléen) :
-
t = 0 s :
-
Vitesse initiale :
-
-
-
Avec : 1.
Exploitation de la chronophotographie : a.
Caractéristique du mouvement suivant l’axe (Ox).
-
Projection du mouvement du centre de
masse G sur l’axe (Ox).
-
Dans la partie centrale :
-
Le point mobile G parcourt des
distances sensiblement égales pendant des durées égales.
-
Elles ne sont pas exactement égales
car la vitesse de départ est élevée et les forces frottement dues à l’air ne sont pas totalement négligeables.
-
Le mouvement de
G sur l’axe (Ox) est
quasi uniforme. b.
Caractéristiques du vecteur accélération.
-
On considère que le poids est la
seule force qui s’applique sur le système
S = (m,
G)
►
Deuxième
loi de Newton.
-
Énoncé :
-
Dans le cas présent :
-
-
Le vecteur accélération a :
-
même direction,
-
même sens et
-
même valeur que le vecteur
-
Le vecteur accélération est vertical
et orienté vers le bas..
►
Coordonnées du vecteur accélération :
-
c.
Vérification des réponses aux deux questions
précédentes.
-
La coordonnée
vx est une primitive de
ax : avec ax
= 0
-
La primitive est connue à une
constante près.
-
Cette constante que l'on note
vox est liée
aux conditions initiales.
-
Elle représente la composante de la
vitesse du mobile suivant l'axe
x'Ox au temps
t = 0.
-
En conséquence, les constantes qui
apparaissent sont liées aux conditions initiales et parfaitement connues à partir des conditions initiales
-
Comme
ax = 0, alors
vx = cte =
v0x = 29,1 m .
s–1
-
Comme,
v0x = 29,1 m .
s–1 = cte, le mouvement est rectiligne uniforme suivant
l’axe (Ox).
-
De même :
ay = – g = –
9,82 m . s–2 , alors
vy = –
g .
t +
v0y
-
vy = –
g .
t +
v0y
-
vy = – 9,82 ×
t +
18,9 (m . s–1)
-
La valeur de la vitesse
vy dépend du temps
t.
-
2.
Exploitation de la courbe vy
= f (t) : a.
Caractéristiques du mouvement suivant l’axe
vertical.
-
Courbe :
-
Le système
S est animé d’un
mouvement rectiligne uniformément varié car son vecteur accélération a toujours la même direction, le même sens
et la même valeur.
-
Le vecteur accélération est un
vecteur constant au cours du temps :
-
La valeur de la vitesse
vy est une fonction affine du temps : vy
= aOy . t + v0y
-
Le mouvement de
G possède 2 phases :
-
Première phase :
-
La valeur de la vitesse
vy diminue, et s’annule lorsque
G atteint sa hauteur maximale
-
Le mouvement de
G sur l’axe (Oy) est
rectiligne uniformément retardé.
-
Deuxième phase :
-
La valeur de la vitesse
vy augmente
-
Le mouvement de
G sur l’axe (Oy) est
rectiligne uniformément accéléré. b.
Position particulière de la trajectoire est
occupée par G à la date pour laquelle vy =
0
-
À la date pour laquelle
vy = 0, le point G
occupe le sommet de la trajectoire.
-
Date à laquelle
vy = 0 :
-
-
Au temps
t ≈ 1,92 s, le vecteur
vitesse à les coordonnées suivantes :
-
-
La composante verticale est nulle,
vy = 0
-
La composante horizontale :
vx ≈ 29,1 m. s–1
-
Valeur de la vitesse :
-
►
Coordonnées du vecteur position
-
-
La coordonnée
x est une primitive de vx :
-
Comme
vx = 29,1 m .
s–1, alors x =
(29,1) ×
t +
x0
-
Avec
x0 =
0 m ,
-
x = 29,1 ×
t
(m)
-
De même :
-
La coordonnée
y est une primitive de vy :
-
Comme
vy = – 9,82 ×
t +
18,9 (m . s–1) , alors
-
y = – 4,91 ×
t2 + 18,9 ×
t + y0
-
Avec
y0 = – 0 m,
-
y = – 4,91 ×
t2 + 18,9 ×
t
-
►
Récapitulatif :
-
Les différentes courbes :
-
Équation de la trajectoire :
-
y =
f (x) :
-
-
On élimine le temps
t pour exprimer y en
fonction de x.
-
►
Portée
horizontale :
-
Portée horizontale : il faut
déterminer la valeur de la longueur
OC,
-
En conséquence il faut trouver
l'abscisse xC
du point C tel que :
-
-
Il faut résoudre l’équation :
-
On rejette la solution
xC = 0
-
►
Flèche : c’est l’altitude maximale
atteinte.
-
-
-
Valeur de
yM : -
-
Le
canal de Corinthe est situé en Grèce. Il a été creusé pour
relier la mer Égée et la
mer Ionienne.
-
Les parois rocheuses sont très hautes
et l'eau s'écoule à 79 m au-dessous du niveau du sol.
-
l’Australien Robbie Maddison a
réalisé l’exploit de franchir le canal de Corinthe à moto en avril
2010.
-
Il a pris son élan pour accélérer sa
moto et atteindre la vitesse de 125
km . h –1 .
-
Il
a ensuite emprunté une rampe qui lui a permis de franchir le canal, avant
d'atterrir de l’autre côté.
-
Le point le plus haut de son vol a
dépassé les 95 mètres au-dessus du niveau de l’eau.
-
À l’instant de date
t = 0, Maddison et sa moto se trouvent à l’origine du repère et
quittent le tremplin.
-
Le vecteur vitesse
-
Le niveau de l'eau du canal de
Corinthe est situé à 79 m au-dessous du niveau du sol.
-
Le point de sortie du tremplin se
situe à 5,7 m au-dessus du niveau du sol.
-
l'Australien a atteint sa rampe
d'élan qui l'a propulsé 85 mètres plus loin.
►
Caractéristiques du saut :
-
Longueur du saut : c’est la portée
horizontale : ℓ = 85 m
-
Hauteur du saut : c’est la flèche :
-
H = 95 – 79 – 5,7
-
H ≈ 10 m
-
Les valeurs trouvées sans prendre en
compte les forces de frottement :
-
La portée horizontale : xC ≈ 112 m et la flèche :
yM ≈ 18,2 m
-
Les différences montrent qu’il est
nécessaire de prendre en compte les forces de frottement.
|
8)- Exercice 21 page 231 : Le mouvement de Vénus :
|
Le mouvement de Vénus : Vénus, deuxième des huit planètes du système solaire en partant du Soleil, est la sixième par masse ou par taille décroissante. La
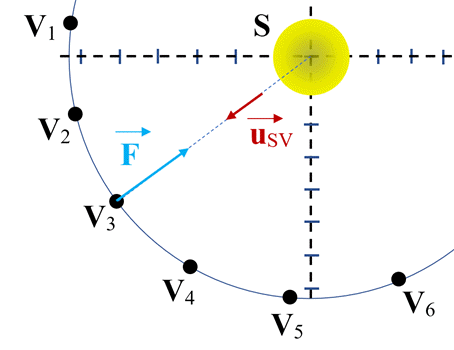
distance Vénus-Soleil est voisine de 0,72 ua. Sa trajectoire autour du Soleil est quasi circulaire. Le site de l’institut de mécanique céleste et le calcul des éphémérides permet d’obtenir, pour une durée au choix, la trajectoire de Vénus dans un référentiel donné. Ci-dessous sont représentées les positions de Vénus tous les 15 jours entre le 1ier
septembre 2019 (V1) et le 29 mars 2020 (V15). 1.
Référentiel d’étude : a.
Dans quel référentiel le mouvement de Vénus
est-il étudié ? b.
Utiliser le schéma fourni pour vérifier la
cohérence entre les informations extraites du pointage et celles du
texte. 2.
On suppose que la vitesse de Vénus autour du
Soleil a une valeur constante v = 34 km . s–1. a.
Construire en V2 et V3
les vecteurs vitesses
b.
Construire en V3 le
vecteur accélération
c.
Indiquer les caractéristiques (direction,
sens et valeur) de ce vecteur. 3.
Force gravitationnelle : a.
Exprimer la force gravitationnelle
b.
Par application de la deuxième loi de
Newton, exprimer le vecteur accélération
c.
Vérifier le caractère galiléen du
référentiel.
-
Données :
-
1 ua = 1,5 × 1011 m
-
Masse de Vénus :
mV = 4,9 × 1024 kg
-
Masse du Soleil :
mS = 2,0 × 1030 kg
-
Constante de gravitation
universelle :
-
G = 6,67 × 10–11
N . m2 . kg–2. |
Le mouvement de Vénus : 1.
Référentiel d’étude : a.
Référentiel d’étude du mouvement de Vénus.
-
Le mouvement de Vénus est étudié par
rapport au Soleil.
-
L’objet de référence est le Soleil.
-
Le référentiel d’étude est le
référentiel héliocentrique.
►
Le référentiel héliocentrique ou de
Copernic.
-
L’origine du repère lié au
référentiel Héliocentrique est située au centre du Soleil.
-
Les axes z’Oz, x’Ox et
y’Oy sont orthogonaux et ils sont orientés vers des étoiles
lointaines supposées fixes.
-
Ce référentiel est commode pour
l’étude des satellites du Soleil (comme Vénus).
-
Dans ce référentiel,
-
On peut considérer que ce référentiel
est galiléen avec une très bonne approximation (précision de l’ordre
de 10–10) b.
Cohérence entre les informations extraites
du pointage et celles du texte.
-
Sa trajectoire autour du Soleil est
quasi circulaire.
-
« positions de Vénus tous les 15
jours entre le 1ier septembre 2019 (V1)
et le 29 mars 2020 (V15) »
-
De plus, le pointage montre que le
centre de masse de Vénus parcourt des arcs quasiment égaux pendant
des durées égales (15 j).
-
Le mouvement est quasiment circulaire
uniforme. 2.
On suppose que la vitesse de Vénus autour du
Soleil a une valeur constante v = 34 km . s–1. a.
Construction en V2 et V3
des vecteurs vitesses
-
Échelle utilisée : 1,0 cm ↔ 10 km . s–1
-
Longueur du représentant de
-
ℓ
≈ 3,4 cm b.
Construction en V3 du
vecteur accélération
-
Tracé de ZOOM
-
Mesure de la longueur de
-
-
Δv2→3 ≈ 14,5
km . s–1
-
Expression de l’accélération.
-
-
Valeur de l’accélération :
-
-
Échelle utilisée :
-
4 cm ↔ 1,0 × 10–2 m . s–2
-
ℓa3 ≈
4,4 cm
-
Schéma : c.
Caractéristiques (direction, sens et valeur)
du vecteur
-
Direction : droite
(V3S)
-
Sens de
V3 →
S
-
Valeur :
a3 ≈ 1,1 × 10–2 m . s–2 3.
Force gravitationnelle : a.
Expression la force gravitationnelle
-
-
Schéma :
b.
Application de la deuxième loi de Newton.
►
Deuxième loi de Newton.
-
Énoncé : Dans un référentiel galiléen,
la
somme des vecteurs forces
de
masse m et de
centre de masse
G,
est
égal au produit de sa masse
m
par
le vecteur accélération
Valeur des forces F en newton (N)
Valeur de la masse m en kilogramme (kg)
Valeur de l’accélération aG en mètre
par seconde au carré (m . s–2)
-
Dans le cas présent :
-
-
Expression du vecteur accélération
-
-
La valeur du vecteur accélération
-
c.
Vérification du caractère galiléen du
référentiel.
-
a ≈
a3
-
La valeur trouvée pour l’accélération
de Vénus avec la construction graphique est cohérente avec celle
trouvée en appliquant la deuxième loi de Newton dans le référentiel
héliocentrique.
-
Le référentiel héliocentrique peut
être considéré comme un référentiel galiléen avec une bonne
approximation.
Pour se promener dans le
système solaire.
![]() et
et
![]() .
.![]() et
et
![]() :
:![]() .
.![]()
![]() :
:![]()
![]() :
: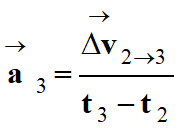
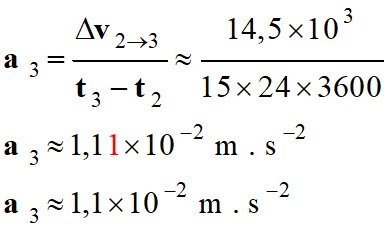
![]() .
.![]() exercée par le Soleil sur
Vénus.
exercée par le Soleil sur
Vénus.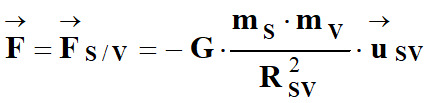
![]() appliquées
à un système S,
appliquées
à un système S,
![]() de son centre de masse.
de son centre de masse.
![]()
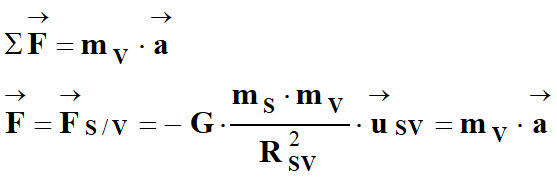
![]() :
: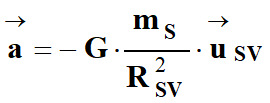
![]() :
: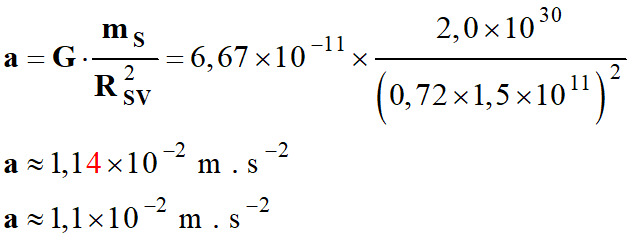
![]()
|
|