QCM réalisé avec le logiciel Questy

Pour s’auto-évaluer

AIDE

Réaction chimique : Tableau d’avancement, bilan de matière

-  Quantité de matière d’ions fer III

-  n₁ = 3,0 × 10^–2 mol = 30 mmol

-  Quantité de matière de zinc métallique :

-  n₂ = 2,0 × 10^–2 mol = 20 mmol

-  Équation bilan de la réaction

- Attention : réponse n₁ – 2 x et 2 x

-  Tableau d’avancement de la réaction :

-  Relations : n₁ – 2 x pour Fe³⁺ (aq) et 2 x pour Fe (s)

Transformation totale :

-  L’équation s’écrit avec

-  une double flèche  si la réaction est non totale ;

-  une simple flèche → si la réaction est totale.

-  Comme l’indique la flèche, la transformation est totale (→)

-  Lorsqu’une réaction est totale, l’avancement final est égal à l’avancement maximal :

-  x_f = x_max

-  Tableau d’avancement et bilan de matière.

-  Exploitation :

-  Valeur de l’avancement maximal :

-  Hypothèse 1 : On considère que l’ion Fe³⁺ (aq) est le réactif limitant :

-  Dans ce cas :  n₁ – 2 x_max1 = 0 => n₁ = 2 x_max = 3,0 × 10^–2 mol 

-  x_max1 ≈ 1,5 × 10^–2 mol 

-  Hypothèse 2 : On considère que Zn (s) est le réactif limitant 

-  Dans ce cas : n₂ – 3 x_max2 = 0 => n₂ = 3 x_max2 = 2,0 × 10^–2 mol

-  x_max2 ≈ 6,7 × 10^–3 mol

-  Conclusion :

-  L’avancement maximal est égal à la plus petite des deux valeurs :

-  x_max = x_max2 ≈ 6,7 × 10^–3 mol < x_max1

-  D’autre part :  

-  On donne n (Zn²⁺ ) = 2,0 × 10^–2 mol

-  On en déduit la valeur de l’avancement final :

-  n (Zn²⁺ ) = 3 x_f = 2,0 × 10^–2 mol => x_f ≈ 6,7 × 10^–3 mol

-  Comme n (Zn) = 0,

-  Zn (s) est le réactif limitant (il est totalement consommé : n₂ – 3 x_f = 0

-  Comme :

-  x_f = x_max, la transformation est totale.

Transformation non totale. Équilibre chimique

Chap N° 07 Sens d’évolution spontanée d’un système chimique

-  Lorsqu’une réaction est totale, l’avancement final est égal à l’avancement maximal :

-  x_f = x_max

-  En présence d’un équilibre chimique (cas d’une réaction non totale) :

-  x_f < x_max

-  Comparer l’avancement final x_f et l’avancement maximal x_max permet de distinguer les transformations totales et non totales.

-  Pour une transformation non totale, il faut connaître la valeur de l’avancement final x_f pour effectuer le bilan de matière à l’état final.

-  Dans le cas d’une transformation non totale :

-  À l’état final :

-  Les quantités des espèces ne varient plus ;

-  Tous les réactifs et les produits coexistent.

-  On est en présence d’un équilibre chimique.

-  Lors d’une réaction non totale :

-  Les réactifs réagissent entre eux pour donner les produits ;

-  Simultanément :

-  Les produits réagissent pour donner les réactifs.

-  Une réaction non totale est modélisée par deux réactions opposées l’une de l’autre.

-  L’équation de la réaction s’écrit alors avec une double flèche  qui traduit le fait que deux réactions, inverses l’une de l’autre, peuvent se produire simultanément dans le système.

-  L’équation s’écrit alors :

a A + b B c C + d D

-  Exemple :

-  x_f = 0,85 mol et x_max = 1,0 mol

-  Tous les réactifs et produits sont présents à l’état final.

Le quotient de réaction :

-  Considérons la réaction chimique non totale suivante :

a . A (aq) + b . B (aq)  c . C (aq) + d . D (aq)

-  Par définition, le quotient de réaction Q_r de cette réaction s’écrit :

►  Remarque :

-  Pour simplifier l’expression, on omet de mettre la concentration standard C⁰.

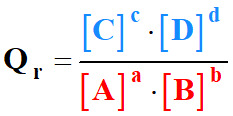
-  Mais, il ne faut pas oublier que le quotient de réaction est une grandeur sans unité qui caractérise un système chimique dans un état donné.

-  Cas d’une réaction où le solvant intervient :

-  Par convention, l’eau, solvant, n’intervient pas dans l’écriture de l’expression de Q_r (même s’il intervient dans l’équation de la réaction.

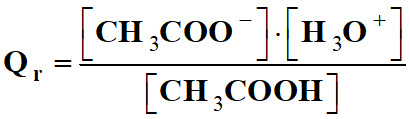
-  Cas d’une réaction avec des espèces solides :

-  Les espèces chimiques solides n’apparaissent pas dans l’expression du quotient de réaction.

►  Exemple : écrire le quotient de réaction de la réaction suivante :

- 

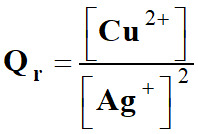
-  Pour la réaction :

-   

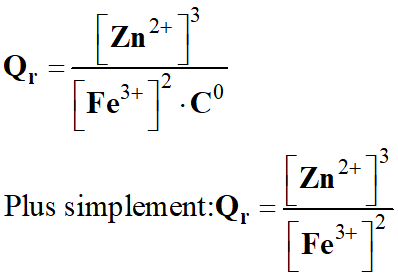
Constante d’équilibre K.

-  Dans l’état d’équilibre d’un système, le quotient de réaction Q_r,éq prend une valeur qui ne dépend pas de l’état initial.

-  La valeur de Q_r,éq est indépendante de la composition initiale.

-  Cette valeur ne dépend que de la température.

-  Elle est appelée constante d’équilibre et on la note K.

K = Q_r,éq

-  La valeur de la constante d’équilibre nous renseigne sur la nature de la réaction chimique.

►  Système chimique hors d’équilibre :

-  Tout système chimique, hors d’équilibre, évolue spontanément vers un état d’équilibre.

-  En conséquence la valeur de Q_r tend vers K

-  À une température donnée, la comparaison du quotient de réaction dans l’état initial, Q_r,i  à la constante d’équilibre K permet de prévoir le sens d’évolution spontanée du système chimique.

►  Premier cas : 

-  Si le quotient de réaction initial Q_r,i est égal à la constante d’équilibre K,

-  Soit Q_r,i = K, le système est déjà à l’équilibre.

-  Il n’évolue pas.

►  Deuxième cas : 

-  Si le quotient de réaction initial Q_r,i est inférieur à la constante d’équilibre K,

-  soit Q_r,i < K,

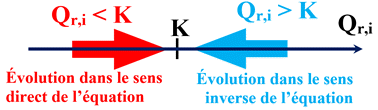
-  Le système chimique évolue spontanément vers un état d’équilibre.

-  Il évolue dans le sens direct de l’écriture de l’équation de la réaction.

►  Troisième cas : 

-  Si le quotient de réaction initial Q_r,i est supérieur à la constante d’équilibre K,

-  soit Q_r,i > K, le système chimique évolue spontanément vers un état d’équilibre.

-  Il évolue dans le sens inverse de l’écriture de l’équation de la réaction.

►  Remarque :

-  Ce critère d’évolution permet de prévoir le sens d’évolution spontanée du système connaissant sa composition initiale.

-  Ce critère ne tient pas compte de l’aspect cinétique de la réaction.

Réaction d’oxydoréduction :

-  Un oxydant est une entité chimique capable de gagner un ou plusieurs électrons.

-  (Oxydant : gagne)

-  Un réducteur est une entité chimique capable de perdre un ou plusieurs électrons.

-  (Réducteur : perd)

-  Couple oxydant / réducteur :

-  À tout couple oxydant / réducteur, on associe la demi-équation électronique d’oxydoréduction suivante :

-  Ceci est une écriture formelle.

-  La double flèche traduit la possibilité de passer d’une forme à l’autre suivant les conditions expérimentales.

-  La transformation chimique qui correspond au passage de l’oxydant Ox à son réducteur conjugué Red est une réduction :  Ox + n e ^– → Red

-  Une réduction est un gain d’électrons.

-  La transformation chimique qui correspond au passage du réducteur Red à son oxydant conjugué Ox est une oxydation : Red → Ox + n e ^–

-  Une oxydation est une perte d’électrons.

-  Au cours d’une réaction d’oxydoréduction, un oxydant est réduit et un réducteur est oxydé.

-  Une réaction d’oxydoréduction est une réaction de transfert d’électrons.

-  Elle fait intervenir deux couples Ox / Red : Ox₁ / Red₁ et Ox₂ / Red₂ 

-  Ox₁ ne peut pas réagir sur Ox₂ et Red₁ ne peut pas réagir sur Red₂

-  Ox₁ peut réagir sur Red₂ ou Ox₂ peut réagir sur Red₁

-  Cela dépend de la force relative des oxydants et des réducteurs mis en présence.

-  Au cours d’une réaction d’oxydoréduction :

-  Un oxydant est réduit et

-  Un réducteur est oxydé.

-  Fe²⁺ → Fe³⁺ + e^– : couple Ox / Red :  Fe³⁺ / Fe²⁺ 

-  Au cour de la réaction suivante :

5 Fe²⁺ + MnO₄^– + 8 H⁺ → 5 Fe³⁺ + Mn²⁺+ 4 H₂O

-  L’ion Fe²⁺ cède un électron pour former Fe³⁺

-  L’ion Fe²⁺ est un réducteur, il subit une oxydation

-  L’ion MnO₄^– est un oxydant, il subit une réduction

Couples oxydant / réducteur :

-  Couples Ox / Red :  Fe³⁺ / Fe²⁺ : MnO₄^– / Mn²⁺

-  Le couple MnO₄ ^– / Mn²⁺.