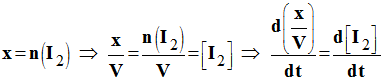|
Contrôle N° 02 Sciences physiques, 2006 Terminale S énoncé et correction |
|
|
I- La chimie au fil du temps.
On réalise l’oxydation des ions iodure I– (aq) (du couple I2 (aq) / I– (aq)) par les ions peroxodisulfate S2O82– (aq) (du couple S2O82– (aq) / SO42– (aq)).
1)- Écrire l’équation de la réaction d’oxydoréduction correspondante.
|
S2O82– (aq) + 2 e – = 2 SO42– (aq) |
|
2 I– (aq) = I 2 (aq) + 2 e – |
|
S2O82–
(aq) + 2
I– (aq)
→ 2 SO42–
(aq) +
I2 (aq) |
Cette transformation est lente.
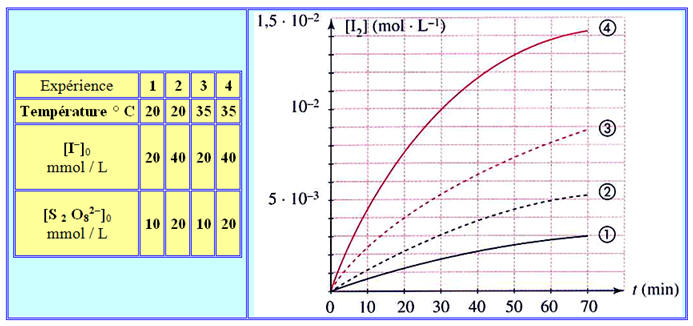
Pour suivre l’évolution en fonction du temps de la concentration en diiode I2 (aq) dans le milieu réactionnel, on réalise quatre expériences dans des conditions différentes puis on trace les courbes [I2] = f (t) correspondantes.
Les conditions expérimentales et les courbes obtenues sont les suivantes.
2)- Par quelles techniques peut-on suivre l’évolution de cette réaction ? Préciser de façon détaillée.
- Les techniques que l’on peut utiliser :
- Une technique chimique : le dosage iodométrique.
- On dose le diiode formé avec une solution titrée de thiosulfate de sodium.
- Comme indicateur de fin de réaction, on utilise l’empois d’amidon.
- Pour arrêter la réaction a une date donnée, on utilise la trempe qui consiste à refroidir brutalement le mélange réactionnel.
- Une technique physique : le suivi spectrophotométrique.
- Le diiode en solution aqueuse donne une solution colorée.
- On mesure l’absorbance A de la solution au cours du temps.
- Grâce à la loi de Beer-Lambert :
- L’absorbance d’une solution diluée contenant une espèce colorée est proportionnelle à la concentration (effective) C de cette espèce et à l’épaisseur ℓ (cm) de la solution traversée par le faisceau lumineux.
- A = ε (λ) . ℓ . C = k . C
- On peut en déduire les variations de la concentration en diiode au cours du temps.
- Remarque :
- ε (λ) est appelé coefficient d’extinction molaire ou coefficient d’absorption molaire.
- Il dépend de la nature de l’espèce dissoute et de la longueur d’onde de la radiation utilisée.
- Il dépend également du solvant et de la température.
- Unité : mol – 1.L.cm – 1
3)- Quels facteurs cinétiques sont ainsi mis en évidence ? Préciser leurs effets. Justifier votre réponse de façon détaillée.
- Les facteurs cinétiques mis en évidence sont :
- La concentration des réactifs et la température.
- Expériences 1 et 3 : Les concentrations des réactifs sont les mêmes, la température change :
- θ1 = 20 ° C et : θ3 = 35 ° C
- Observons les différentes courbes [I2] = f (t) :
-
La courbe
 se trouve au-dessous de la
courbe
se trouve au-dessous de la
courbe  .
.
- Pour une même durée, [I2]1 < [I2]3.
- En conséquence, l’avancement temporel de la réaction augmente avec la température et la vitesse de la réaction augmente avec la température θ. La température est un facteur cinétique.
- Expériences 1 et 2 : La température θ est la même, mais les concentrations des réactifs ont été doublées.
- Observons les différentes courbes [I2] = f (t) :
-
La courbe
 se trouve au-dessous de la
courbe
se trouve au-dessous de la
courbe  .
.
- Pour une même durée, [I2]1 < [I2]2.
- En conséquence, l’avancement temporel de la réaction augmente avec la des réactifs et la vitesse de la réaction augmente avec la concentration des réactifs.
- La concentration des réactifs est un facteur cinétique.
4)- Le volume du mélange réactionnel lors de l’expérience 1 est V = 100 mL. Déterminer la valeur de l’avancement maximal xmax de la réaction. En déduire la valeur de la concentration en diiode correspondante.
- Le plus simple est d’utiliser le tableau d’avancement de la réaction
|
Équation |
S2O82–
(aq) |
+
2 I–
(aq) |
→ |
2 I–
(aq) |
+ 2
SO42–
(aq) |
|
|
état |
Avanc. x
(mol) |
|
|
|
n
t (I
2) |
|
|
État initial (mol) |
0 |
n 0 (S2O82–) |
n 0 (I–) |
|
0 |
0 |
|
Au cours
Trans. |
x(t) |
n 0 (S2O82–)
- x |
n 0 (I–)
– 2 x |
x |
2
x |
|
|
Av. max (mol) |
x max |
n 0 (S2O82–)
- xmax |
n 0 (I–)
– 2 xmax |
|
xmax |
2
xmax |
- Quantités de matières des réactifs à l’instant initial :
- Quantité de matière de diiode :
-
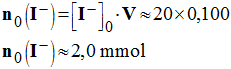
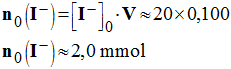
- Quantité de matière d’ions peroxodisulfate :
-
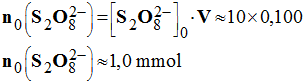
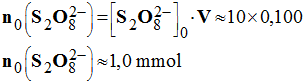
- Il faut résoudre le système d’inéquations :
-
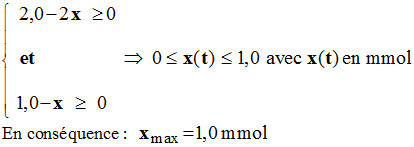
- Concentration en diiode correspondante :
-
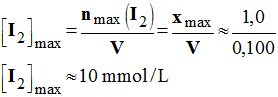
5)- Définir la vitesse volumique d’une réaction chimique. Sachant que x = n (I2) à chaque instant, déterminer la valeur de la vitesse de la réaction chimique lors de l’expérience 4 à la date t = 20 min. Préciser la méthode utilisée.
- Définition : La vitesse volumique de réaction v(t) à la date t, est la dérivée par rapport au temps,
- Du rapport entre l’avancement x de la réaction et le volume V du milieu réactionnel.
-
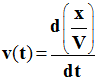
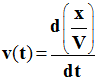
- Lorsque l’on travaille à volume constant, on obtient la relation suivante :
-
Relation :
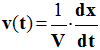
- Pour déterminer la valeur de la vitesse de réaction, on trace la tangente à la courbe [I2] = f (t), car
-
En conséquence :
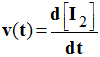 .
.
- La valeur du coefficient directeur de la tangente donne la valeur de la vitesse à l’instant considéré.
- On trace la tangente à la courbe [I 2] = f (t) relative à l’expérience 1 au temps t = 20 min.
Tracé
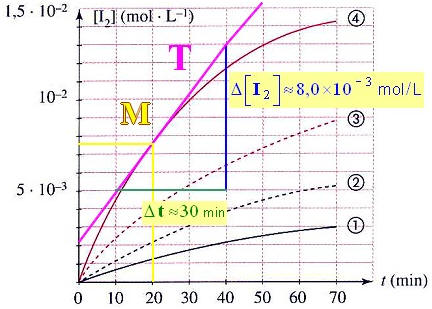
- Δt ≈ 30 min et Δ[I2] ≈ 8,0 x 10 – 3 mol / L
-
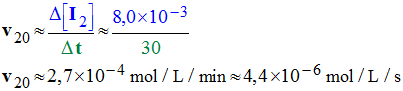
II- Bilan énergétique et désintégration alpha.
Le radium
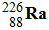 , de demi – vie
t ½ = 1600 ans, émet une particule radioactive
a avec production de radon
Rn et un rayonnement γ.
, de demi – vie
t ½ = 1600 ans, émet une particule radioactive
a avec production de radon
Rn et un rayonnement γ.
1)- écrire l’équation de la réaction de désintégration.
- Équation bilan de la réaction de désintégration :
-
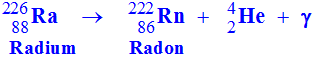
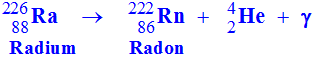
2)- Que représente la grandeur  ? Calculer sa valeur.
? Calculer sa valeur.
- La grandeur τ représente la constante de temps.
- Elle s’exprime en seconde s : τ ≈ 7,28 × 10 10 s
3)- Donner l’expression littérale de la perte de masse au cours de cette réaction.
-
Perte de masse : |Δm| = |mf
– mi | = |(mα + mRn) – mRn
|
- Au cours d’une réaction radioactive, la masse du système diminue.
4)- Calculer la valeur de la perte de masse en unité de masse atomique.
- Valeur de la perte de masse en unité de masse atomique :
-
|Δm| = |mf – mi
| = |(mα + mRn) – mRn
|
-
|Δm| ≈ |(4,00150 + 221,97027) –
225,97700|
-
|Δm| ≈ 0,00523 u
5)- Donner l’expression littérale de l’énergie dissipée E lors de la désintégration d’un noyau de radium au repos. Justifier cette expression.
- Au cours de la réaction, la masse du système diminue, le système libère de l’énergie.
- Cette énergie est dissipée vers le milieu extérieur sous forme d’énergie cinétique et de rayonnement.
-


6)- Calculer cette énergie E en MeV et en joule. En déduire l’énergie dissipée pour une mole de radium en joule.
-
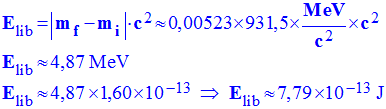
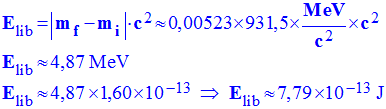
-
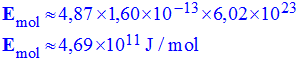
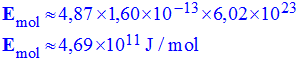
|
Données |
|
|
Masse d’un noyau : Masse d’un noyau de radon : mRn = 221,97027 u Masse d’une particule alpha : mα = 4,00150 u |
Nombre d’Avogadro :
1 MeV = 1,60 × 10 – 13 J 1 u = 931,5 MeV / c² |