I- La chimie au fil du temps.

On réalise l’oxydation des ions iodure I^– _(aq) (du couple I_{2 (aq)} / I^– _(aq)) par les ions peroxodisulfate S₂O₈^2– _(aq) (du couple S₂O₈^2– _(aq) / SO₄^2– _(aq)).

1)- Écrire l’équation de la réaction d’oxydoréduction correspondante.

 

Cette transformation est lente.

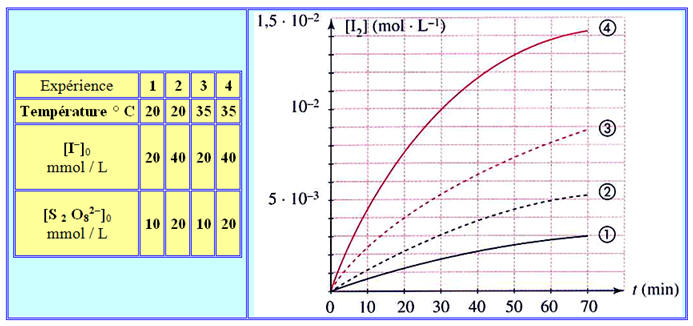
Pour suivre l’évolution en fonction du temps de la concentration en diiode I _{2 (aq)} dans le milieu réactionnel, on réalise quatre expériences dans des conditions différentes puis on trace les courbes [I₂] = f (t)  correspondantes.

Les conditions expérimentales et les courbes obtenues sont les suivantes.

 

2)- Par quelles techniques peut-on suivre l’évolution de cette réaction ? Préciser de façon détaillée.

3)- Quels facteurs cinétiques sont ainsi mis en évidence ? Préciser leurs effets. Justifier votre réponse de façon détaillée.

4)- Le volume du mélange réactionnel lors de l’expérience 1 est V = 100 mL. Déterminer la valeur de l’avancement maximal x_max de la réaction. En déduire la valeur de la concentration en diiode correspondante.

5)- Définir la vitesse volumique d’une réaction chimique. Sachant que x = n (I₂) à chaque instant, déterminer la valeur de la vitesse de la réaction chimique lors de l’expérience 4 à la date t = 20 min. Préciser la méthode utilisée.

II- Bilan énergétique et désintégration alpha.

Le radium , de demi – vie t ½ = 1600 ans, émet une particule radioactive a avec production de radon Rn et un rayonnement γ.

1)- écrire l’équation de la réaction de désintégration.

2)- Que représente la grandeur  ? Calculer sa valeur.

3)- Donner l’expression littérale de la perte de masse au cours de cette réaction.

4)- Calculer la valeur de la perte de masse en unité de masse atomique.

5)- Donner l’expression littérale de l’énergie dissipée E lors de la désintégration d’un noyau de radium au repos. Justifier cette expression.

6)- Calculer cette énergie E en MeV et en joule. En déduire l’énergie dissipée pour une mole de radium en joule.