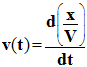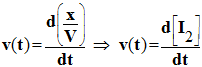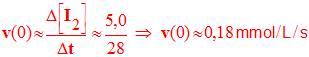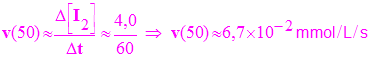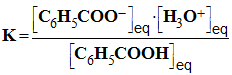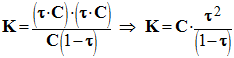1)- Oxydation des ions iodure par les ions peroxodisulfate (2,5 pts).

La réaction entre les ions iodure I ^– (aq) et les ions peroxodisulfate S₂O₈^{2 –} (aq) est une réaction lente dont l’équation s’écrit :        

S₂O₈^{2 –} (aq)   +   2 I ^– (aq)   →   I₂ (aq)   + 2 SO₄^{2 –} (aq)

Les ions sont incolores et I₂ (aq)  a une teinte jaune – orangé en milieu aqueux.

a)-   Proposer une méthode chimique et une méthode physique permettant de

suivre l’évolution de cette réaction au cours du temps.

-  méthode chimique et une méthode physique

-  Méthode chimique : on dose le diiode formé par une solution de thiosulfate de sodium.

-  Pour arrêter la réaction à une date donnée, on réalise la trempe.

-  Méthode physique :

-  On utilise un spectrophotomètre pour suivre l’évolution de la réaction.

-  On mesure l’absorbance du mélange réactionnel en fonction du temps.

-  La loi de Beer-Lambert permet de connaître les variations de la concentration en diiode au cours du temps.

Lors d’une étude cinétique, on a déterminé, à différents instants, la concentration en diiode [ I₂ ] du mélange réactionnel.

Les résultats sont rassemblés dans le tableau suivant.

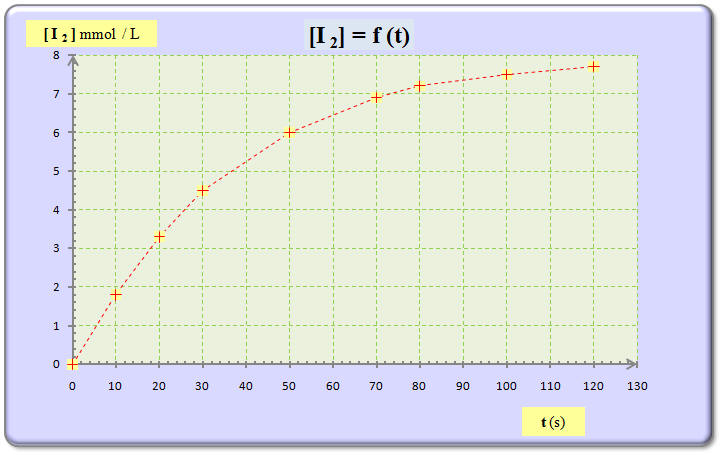
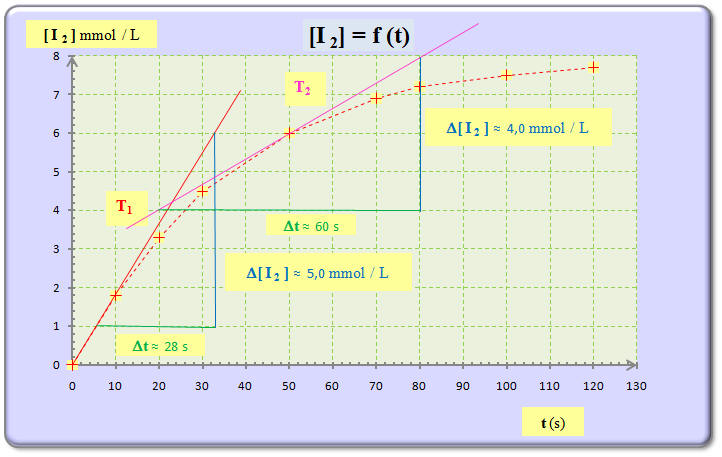
b)-   Tracer la courbe représentative de l’évolution de la concentration en diiode

[I₂] du mélange réactionnel en fonction du temps.

-  Courbe [I₂] = f (t).

Échelles : 1 cm ↔ 10 s et 2 cm ↔ 1 mmol / L.

 Cliquer sur l'image pour l'agrandir

c)-   Définir la vitesse volumique de réaction v.

d)-   Relier la vitesse volumique de réaction v à la concentration en diiode [I₂] du mélange réactionnel.

-  À chaque instant t, dans le mélange réactionnel, la quantité de matière de diiode formé s’identifie avec l’avancement temporel de la réaction :

-   

-   

e)- Déterminer la valeur de la vitesse :

-  À l’instant t = 0 s,

-  À l’instant t = 50 s.

-  valeur de la vitesse :

-  À l’instant t = 0 s :

-  On trace la tangente à la courbe au point M₁ d’abscisse t = 0 et on détermine la valeur du coefficient directeur :

-   

-  À l’instant t = 50 s :

-  On trace la tangente à la courbe au point M₂ d’abscisse t = 50 s et on détermine

la valeur du coefficient directeur :

-   

-  Exploitation graphique :

 Cliquer sur l'image pour l'agrandir

f)-  Commenter l’évolution de la vitesse au cours du temps.

-  Commentaire :

-  La vitesse d’une transformation chimique est maximale à l’instant initial.

-  Elle décroît ensuite et s’annule lorsque la réaction est terminée.

-  Les réactifs sont consommés au fur et à mesure que la réaction se poursuit.

-  Comme la concentration des réactifs est un facteur cinétique, la diminution de la concentration des réactifs entraîne la diminution de la vitesse.

2)- pH d’une solution d’acide benzoïque (3,5 pts)

On prépare une solution d’acide benzoïque en dissolvant une masse m = 1,22 g d’acide benzoïque (solide blanc) dans de l’eau distillée.

On obtient un volume V = 2,00 L de solution.

a)- Déterminer la valeur de la concentration molaire C de la solution d’acide benzoïque obtenue.

-  concentration molaire C de la solution d’acide benzoïque obtenue.

-   

b)-   Écrire l’équation de la réaction entre l’acide benzoïque et l’eau et dresser le tableau d’avancement de la réaction.

-  réaction entre l’acide benzoïque et l’eau et tableau d’avancement de la réaction.

c)-   Déterminer une expression de K, constante d’équilibre de la réaction, ne faisant intervenir que la concentration molaire C

de la solution d’acide benzoïque et le taux d’avancement final τ de la réaction. (0,75)

-  L’eau est le solvant, il est en large excès.

-  L’acide benzoïque est le réactif limitant.

-  Expression de K :

(1)

d)-   Que représente cette constante l’équilibre K ?

-  Cette constante K = K_A est  la constante d’acidité de l’acide benzoïque.

-  Cette constante d’équilibre K représente la valeur du quotient de réaction à l’équilibre.

On donne la valeur de la constante de la réaction étudiée :

K = 6,4 × 10 ^{– 5}  à 25 ° C.

e)-   Calculer le taux d’avancement final τ de la réaction. Justifier.

-  Taux d’avancement de la réaction :

-  (2)

-  Le tableau d’avancement de la réaction permet d’écrire :

-  (3)

-  En combinant (2) et (3) :

-  (3’)

-  (4)

-  En combinant (3) et (4) :

-  (5)

-  En combinant (1), (3’) et (5) :

-  (6)

-  Cette constante d’équilibre K représente la valeur du quotient de réaction à l’équilibre.

-  taux d’avancement final τ de la réaction :

-  De la relation (6), on tire : C. τ ²  +  K . τ  – K = 0.

-  En remplaçant les lettres par leur valeur respective :

-  5,0 × 10 ^{– 3}  τ ²  +  6,4 × 10 ^{– 5}  τ  – 6,4 × 10 ^{– 5}  = 0

-  Cette équation du second degré admet deux solutions :

-  τ₁ ≈ 0,11 et τ₂ ≈ – 0,12

-  Or  0  ≤  τ  ≤  1, en conséquence, la bonne solution est τ₁ ≈ 0,11

f)-  Calculer l’avancement final x_f et l’avancement volumique final  de la réaction.

-  Avancement final :

-  x_f = τ . n

-  x_f = τ . C . V

-  x_f ≈ 0,11 × 5,0 × 10 ^{– 3} × 2,00

-  x_f ≈ 1,1 × 10 ^{– 3} mol

-  Avancement volumique final :

-   

g)-  En déduire la valeur du pH de la solution d’acide benzoïque. Justifier.

-  Valeur du pH de la solution :

-  pH = – log [H₃O ⁺] or 

-  pH = – log [H₃O ⁺] ≈ – log (5,5 × 10 ^{– 4})

-  pH ≈ 3,3