|
Bac Blanc : Exercice 1
Une équation au service
des sciences physiques |
Énoncé |
Exercice 1 : Une équation au
service des Sciences Physiques (6 points)
![]()
|
L'équation différentielle
permet de décrire un grand nombre de phénomènes physiques variables au cours du temps:
intensité, tension, vitesse.
On rappelle que mathématiquement cette équation admet en
particulier 2 solutions :
|
PARTIE A : DANS LE DOMAINE DES SYSTÈMES ÉLECTRIQUES.
|
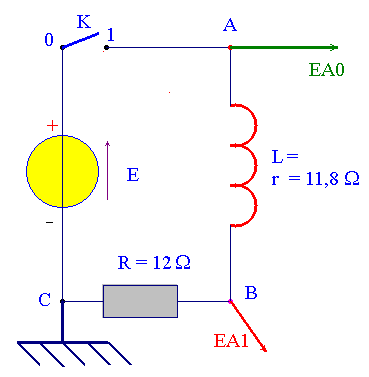
Cette première partie tend à montrer la validité du modèlepour un circuit électrique mettant en jeu : une bobine d'inductance L et de résistance r = 11,8 Ω ,(donc non négligeable), et un conducteur ohmique de résistance R = 12 Ω, alimenté par un générateur délivrant une tension continue E = 6,1 V. On réalise expérimentalement le circuit électrique ci-dessous.
L'évolution des grandeurs
variables, tension u
(t) et
intensité
i (t), est obtenue par voie informatique. |
 |
|
I- Étude expérimentale
La courbe expérimentale donnant l'évolution de l'intensité
i (t), obtenue
par traitement informatique est donnée en ANNEXE, graphique 1.
1)- Quelle tension visualise-t-on à la voie
EA0 ?
2)- Quelle tension visualise-t-on à la voie
EAl ? Pourquoi peut-on en
déduire les variations de l'intensité i
(t).
3)- Évaluer graphiquement la durée du régime transitoire. Aucune
justification
n'est demandée.
4)- La grandeur τ
étant la constante de temps associée au dipôle
{bobine-conducteur
ohmique} :
- Déterminer la valeur de τ
à l’aide du graphique avec la méthode de votre choix.
5)- Donner l'expression littérale de τ
en fonction des paramètres du circuit.
6)- En déduire l'expression de l'inductance de la bobine et calculer sa
valeur.
II- Modèle théorique
1)- En utilisant la loi d'additivité des tensions et en respectant
l'orientation du
circuit, établir l'équation différentielle vérifiée par
l'intensité i
(t).
2)- Par identification avec l'équation
(1) vérifier que
3)- En déduire l'équation horaire littérale i (t) en fonction de {r, R, L et E}.
Montrer que cette solution valide bien l'équation
établie en 2.1.
4)- Montrer que cette équation horaire peut s'écrire :
III- Confrontation des résultats expérimentaux avec le modèle théorique.
On rappelle que
1)- On appellera I l'intensité en régime permanent (l'intensité étant constante).
Donner
l'expression littérale de I.
Calculer sa valeur. Est-elle en accord avec la valeur expérimentale
obtenue ? 2)- Donner l'expression littérale de i (t) à la date t = τ en fonction de I.
Calculer sa valeur. Est-elle en accord avec l'expérience ?
|
PARTIE B : DANS LE DOMAINE MÉCANIQUE.
|
L'étude de la chute d'une bille d'acier, de masse m, dans un fluide de masse volumique ρ fluide a été exploitée grâce à un logiciel. Les capacités du logiciel permettent ensuite de faire tracer l'évolution de la vitesse du centre d'inertie en fonction du temps, v (t).
La courbe expérimentale et modélisée est proposée en ANNEXE,
graphique 2.
I- Exploitation de l'équation v (t) modélisée.
L'équation mathématique associée à la courbe modélisée, vérifie
Cette équation est identifiable à l'équation (2).
1)- Déterminer la
valeur de
α
et du rapport
2)- Montrer que
l'équation différentielle ayant l'équation
(3) pour solution
vérifie
l'écriture numérique
3)- Déterminer la valeur de la vitesse limite à l’aide de cette équation numérique. Justifier. Le résultat est-il en accord avec la valeur expérimentale ?
II- Étude du phénomène physique. 1)- Faire l'inventaire des forces appliquées à la bille. Les représenter sur un schéma, en sens et direction appliquée au centre d'inertie G de la bille. 2)- Appliquer au système bille la seconde loi de Newton.
III- Exploitation de la modélisation
La bille ayant servi à réaliser l'étude est une bille d'acier de masse
m =
L'accélération de la
pesanteur est g =
Les forces de frottement qui s'appliquent à la bille ont pour expression 1)- En utilisant un axe vertical (Ox) orienté vers le bas, montrer que l'équation différentielle relative à la grandeur variable v (t) vérifie
2)- En
déduire l'expression littérale des coefficients
α
et β de
l'équation (1). 3)- Quelle serait la valeur du coefficient β si la poussée d'Archimède était nulle ? En utilisant l'équation établie en 1.2., justifier que cette force doit être prise en compte. |
Graphique 1 :
Graphique 2 :
 .
. (3),
avec v (t)
en m.s –1 et t en
s.
(3),
avec v (t)
en m.s –1 et t en
s.
 .
.
