I- Travail d’une force constante.

1)- Notion de travail d’une force.

a)-  Caractéristiques d’une force :

-  Schéma :

-  Ressort que l’on tend à l’aide d’une ficelle.

 

-  La force exercée par la ficelle (L) sur le ressort (R) peut être modélisée par un vecteur noté .

-  Ce vecteur indique la direction et le sens de l’action exercée par L sur R.

-  La norme du vecteur est égale à l’intensité de la force, la valeur de la force que l’on note :

-  Elle s’exprime en newton N

-  Pour représenter le vecteur force, une échelle est nécessaire. Exemple : 1 cm ↔ 1 N

-  Représenter la force  sachant que F_L/R = 5,0 N

 

-  L’origine : point d’application de la force, point où l’on considère que la force s’exerce (ici point A).

-  La direction et le sens sont ceux de la force (ici la droite (AB) pour la direction et de A vers B pour le sens).

-  La longueur du représentant est proportionnelle à la valeur de la force.

-  L’unité de force est le newton (N).

-  La valeur d’une force se mesure à l’aide d’un dynamomètre.

b)-  Effets d’une force :

-  Une force qui s’exerce sur un corps peut mettre cet objet en mouvement, modifier sa trajectoire, modifier sa vitesse.

-  L’effet d’une force sur le mouvement d’un système est d’autant plus grand que la masse du système est faible.

c)-  Notion de travail d’une force :

-  Le travail est une grandeur algébrique qui permet d’évaluer l’effet d’une force sur l’énergie d’un objet en mouvement.

-  Dans la vie de tous les jours, on associe la notion de travail à la notion d’effort.

-  Lorsque la force exercée sur un mobile a un effet sur la valeur de la vitesse du mobile, on dit qu’elle travaille.

-  Une force travaille, si son point d’application se déplace dans une direction qui n’est pas perpendiculaire à celle de la force.

-  Une force ne travaille pas si :

-  Sa direction est perpendiculaire à la trajectoire de son point d’application.

-  Son point d’application ne se déplace pas.

-  Le travail constitue un mode de transfert de l’énergie.

-  L’unité de travail est le joule (J).

2)- Travail d’une force constante.

Travail d'une force constante : -  Le travail d’une force constante  dont le point d’application M se déplace de A à B sur le segment [AB] est égal au produit scalaire du vecteur force  par le vecteur déplacement .

 

-  On note :

 

-  Schéma :

 

-  Calculer le travail de la force  sachant que : F = 10 N, ℓ = 7,70 cm et α = 30 °.

-   

-  Remarque :

-  Si le déplacement n’est pas rectiligne, la définition du travail reste la même.

-  Cas particuliers :

-  En conséquence :

 

3)- Le travail du poids.

-  Sur une zone étendue à quelques kilomètres, on peut considérer le vecteur poids  est une force constante.

-  La valeur du poids P = m.g.

-  La grandeur g dépend de l’altitude et de la latitude.

-  Pour un déplacement de quelques kilomètres on peut considérer que g = c^te.

-  Exemple : Solide sur un plan incliné.

-  Considérons un mobile autoporteur de masse m = 400 g se déplaçant sur un plan incliné d’un angle β = 26,2 ° par rapport à l’horizontale.

 

-  Que peut-on dire du travail de la force , réaction du support sur le même trajet AB ?

-  Donner l’expression du travail du poids  sur le trajet AB.

-  Utiliser le fait que le vecteur  est une force constante.

-  En déduire l’expression du travail du poids  sur le trajet AB en fonction de la dénivellation h entre les positions A et B du mobile.

-  Le travail du poids  sur le trajet AB est-il moteur ou résistant ?

-  On choisit un axe vertical Oz, vertical, orienté vers le haut et d’origine O.

-  Lorsque le mobile occupe la position A, il a l’altitude z_A et lorsqu'il occupe la position B, il a l’altitude z_B.

-  Exprimer le travail du poids sur le trajet AB en fonction de z_A et z_B. Conclusion.

-  Calculer la valeur du travail du poids  sur le trajet AB sachant que AB = 10,0 m.

-  Le travail de la force , réaction du support, sur le même trajet AB est nul car la réaction du support est perpendiculaire au support.

-  Les frottements sont négligeables (mobile autoporteur)

-  Expression du travail du poids  sur le trajet AB.

-   

-  On va utiliser deux propriétés du poids :

-  La direction du poids est la verticale du lieu et la valeur du poids est constante.

-  Le poids est une force constante.

-  On choisit le chemin suivant : AH et HB.

-   

-  Avec h = AB . cos α

-  Le travail du poids  sur le trajet AB est un travail moteur :

-   

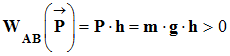
-  Pour donner le travail du poids en fonction de z_A et z_B, il faut donner l’expression des vecteurs  et  en utilisant l’axe Oz et le vecteur unitaire .

-  On peut écrire que :

-     (1)

-      (2)

-  En conséquence : 

-   

-  Conclusion :

-  Lorsque le centre de gravité G d’un corps passe d’un point A à un point B, le travail du poids ne dépend que de l’altitude z_A du point de départ et de l’altitude z_B du point d’arrivée :

-   

-  Le travail du poids ne dépend pas du chemin suivi.

 Si le travail d’une force est indépendant du chemin suivi, c’est-à-dire s’il ne dépend que des positions du point de départ A et du point d’arrivée B, on dit que la force est conservative.

 Le poids est une force conservative.

 Une force est conservative si le travail de cette force est indépendant du chemin suivi, c’est-à-dire s’il ne dépend que des positions du point de départ A et du point d’arrivée B.

 

-   

-  Remarques : 

-  Si z_A > z_B, l’altitude du point G a diminué : le travail du poids est moteur.

-  Si z_A < z_B, l’altitude du point G a augmenté : le travail du poids est résistant.

-  Si z_A = z_B, l’altitude du point G n’a pas changé : le travail du poids est nul.

-  Pour déterminer la valeur du travail du poids, on peut utiliser la relation suivante :

-   

-  Attention au signe :

-  Pour utiliser cette relation, il faut savoir si le travail est résistant ou moteur :

-  Si le travail est moteur :

-   

-  Si le travail est résistant, alors :

-   

-  Valeur du travail du poids :

-   

4)- Travail d’une force électrostatique.

a)-  Expression du travail de la force électrostatique.

-  Considérons une particule de charge q, assimilée à un point matériel M, qui se déplace d’un point A à un point B dans un champ électrostatique uniforme .

-  Dans un champ électrostatique uniforme , la particule M est soumise à une force électrostatique constante :

-   

-  Expression du travail de la force électrostatique   sur le trajet AB ?

-  Schéma : On considère le cas où la charge q > 0 pour pouvoir représenter la force .

 

-  Lorsque la particule, de charge q se déplace du point A au point B, dans l’espace où règne le champ électrostatique uniforme , le travail de la force électrostatique est donné par la relation :

-   

-  Avec ℓ = AB . cos α

-   

b)-  Différence de potentiel.

-  Schéma :

 

 Par définition, la différence de potentiel entre deux points M et N placés dans un champ électrostatique uniforme  est donnée par la relation :

-   

 

-  cette différence de potentiel dépend : du champ électrostatique uniforme  et des positions des points M et N.

c)-  Retour sur l’expression du travail de la force électrostatique :

-  Autre expression du travail de la force électrostatique :

-   

d)-  Conclusion :

-  Une particule de charge q, placée dans un champ électrostatique   est soumise à une force .

-  Lorsque cette particule se déplace d’un point A à un point B, le travail de la force  est donnée par la relation :

-   

-  Remarque : Cette écriture se rapproche de celle du travail du poids sur le trajet AB :

-   

-  Dans un champ électrostatique uniforme, le travail de la force électrostatique à laquelle est soumise la particule ne dépend que des potentiels électriques (liés aux positions) de son point de départ et de son point d’arrivée.

-  La force électrique  est une force conservative.

-  Le travail de la force électrostatique  ne dépend pas du chemin suivi.

 

-   

 

5)- Force non-conservative : cas des forces de frottements.

  On lance avec une vitesse  un palet sur un sol lisse. Le palet glisse, sa vitesse diminue, puis le palet s'arrête.

-  Que se passe-t-il ? Quelles sont les actions mécaniques que subit le palet ?

-  Comme la vitesse du palet diminue, le palet n'est pas pseudo isolé, il n'est pas soumis à des forces dont les effets se compensent.

-  La réaction du support  n'est pas perpendiculaire au support, elle s'oppose au mouvement du palet.

-  On peut décomposer cette réaction :

-  En une réaction normale qui compense le poids

-  Et en une réaction tangentielle , due aux forces de frottement qui ralenti le palet.

-  Avec

-  On se limite à l’étude d’un mouvement rectiligne, sur le trajet AB, au cours duquel l’intensité de la force de frottement est supposée constante.

-  Le travail de la force est donné par définition, par la relation :

-   

-  Dans le cas présent, la force de frottement s’oppose au déplacement du palet, elle est de sens opposée au vecteur déplacement :

-  On dit que ce travail est résistant.

-  Le travail de la force de frottement dépend du chemin suivi : la force de frottement est une force non conservative.

II- Les transferts énergétiques.

1)- Forces conservatives et énergies potentielles.

a)-  Énergie potentielle de pesanteur.

-  À toute force conservative, on associe une énergie potentielle.

-  Dans le cas de la force de pesanteur :

-  Lorsque le centre de gravité G d’un corps passe d’un point A à un point B, le travail du poids ne dépend que de l’altitude z_A du point de départ et de l’altitude z_B du point d’arrivée :

-   

-  L’axe (Oz) est un axe vertical orienté vers le haut.

 

-  L’énergie potentielle de pesanteur E_PP d’un système S de masse m est l’énergie qu’il possède du fait de sa position par rapport à la Terre, c’est-à-dire du fait de son altitude.

-  Un solide de masse m est soumis à son poids  sur la Terre.

-  L’énergie potentielle de pesanteur d’un système S est l’énergie qu’il possède du fait de son interaction avec la Terre.

-  La valeur de cette énergie dépend de la position du système S par rapport à la Terre.

-  Expression : E_PP = m . g . z.

-  Remarque 1 :

-  La valeur de l’énergie potentielle de pesanteur dépend de la valeur de z, elle dépend du choix de l’origine des altitudes.

-  L’énergie potentielle est définie à une constante additive près.

-  La différence d’énergie potentielle ne dépend pas du choix de l’origine.

-  Pour les exercices, on choisit l’origine la plus commode, celle qui simplifie les calculs.

-   

-  Le travail du poids d’un système S se déplaçant entre deux points A et B est égal à l’opposé de la variation de son énergie potentielle de pesanteur entre ces deux points.

b)-  Énergie potentielle électrique.

-  Cas de la force électrostatique :

 

-   

-  Par analogie avec la force de pesanteur, en choisissant une origine des potentiels, on peut définir l’énergie potentielle électrique d’une particule de charge q en un point de potentiel V.

-  E_Pe = q . V

-  En conséquence :

-   

-  Le travail de la force électrostatique exercée sur un système se déplaçant d’un point A à un point B est égal à l’opposé de la variation de son énergie potentielle électrique entre ces deux points.

c)-  Conclusion :

-  La variation d’énergie potentielle d’un système se déplaçant d’un point A à un point B est égale à l’opposé du travail effectué par les forces conservatives de somme  qui s’exercent sur ce système :

-   

2)- Conservation de l’énergie mécanique.

a)-  Expression de l’énergie mécanique d’un système S :

► Énergie potentielle de pesanteur :

 

-  On choisit de façon arbitraire : E_PP (O) = 0

-  Le solide S de masse m, à l’altitude z_A possède l’énergie potentielle de pesanteur :

-  E_PP (A) = m . g . z_A

► Énergie cinétique :

 L’énergie cinétique E_C d’un solide en mouvement de translation est égale au demi-produit de la masse m du solide par le carré de la vitesse v² du solide.

-  On écrit :

-   

-  Unités :

-  L’énergie cinétique caractérise un solide en mouvement.

-  Elle est :

-  Proportionnelle à la masse m du solide

-  Proportionnelle au carré de la vitesse v du solide.

-  Elle dépend du référentiel d’étude.

-  C’est une grandeur supérieure ou égale à zéro.

► Énergie mécanique d’un solide.

 L’énergie mécanique d’un solide est la somme de son énergie cinétique et de son énergie potentielle.

-  Relation :

-  E_m = E_C +  E_P.

-  Unité : joule (J)

b)-  Étude énergétique de la chute libre.

  Expérience :

-  On filme, à l’aide d’une WebCam, la chute d’une balle de golf de masse m = 44 g.

 

-  Tableau de valeurs et pointages :

-  On réalise les pointages à l’aide du logiciel AVIMECA 2.7.

-  Les propriétés du clip sont les suivantes :

 

-  Pour connaître la valeur de la vitesse à chaque instant à l’aide du tableur, on calcule la vitesse moyenne pendant un intervalle de temps très court (ici 80 ms) encadrant l’instant considéré :

 

-  On utilise la colonne E pour l’étude de la vitesse da bille.

-  On prend modèle sur les autres colonnes pour la mise en forme.

-  La vitesse initiale (au temps t = 0 s) :

-  on lâche la balle sans vitesse initiale : la vitesse initiale est nulle.

-  Pour calculer la valeur de la vitesse du point N° 2, on utilise la méthode déjà utilisée :

-  On calcule la vitesse moyenne pendant un intervalle de temps très court encadrant l’instant considéré :

-  On tape la formule suivante dans la cellule E8 : = ABS (D9 – D7) / 0,08

-  Le signe égale : pour signifier à Excel que l’on tape une formule

-  ABS () car on calcule la valeur de la vitesse qui est une grandeur positive

-  L’intervalle de temps vaut : 2 t = 80 ms.

-  On recopie cette formule vers le bas autant que nécessaire avec la souris (copier – glisser)

-  On représente sur un même graphe, les variations de l’énergie cinétique, de l’énergie potentielle et le l’énergie mécanique en fonction du temps.

-  On choisit comme origine de l’énergie potentielle la position initiale de la balle.

-  Tableau de valeurs :

-  Graphe 1 : E = f (t)

 

► Remarque :

-  L’énergie cinétique E_C augmente au cours du temps, l’énergie potentielle E_P diminue au cours du temps, alors que l’énergie mécanique E_m se conserve au cours du temps.

► Conclusion :

-  Le système S, au cours de la chute, est soumis à son poids .

-  Les forces de frottements sont négligeables dans les conditions de l’expérience (balle de petite dimension et hauteur de chute de faible dimension)

-  L’énergie mécanique d’un système S soumis à des forces conservatives est constante, elle se conserve.

-  Au cours du mouvement, la variation de l’énergie mécanique : ΔE_m = 0

-  ΔE_C + ΔE_P = 0  =>  ΔE_C = – ΔE_P

-  Lorsqu’il y a conservation de l’énergie mécanique, il y a transfert total de l’énergie potentielle en énergie cinétique.

3)- Non-conservation de l’énergie mécanique.

a)-  Expérience :

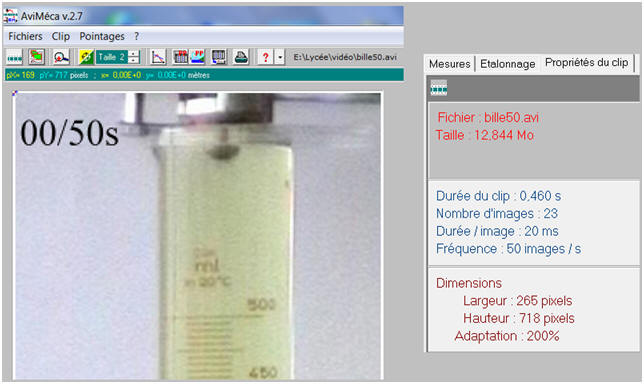
  On filme, à l’aide d’une WebCam la chute d’une bille dans l’huile contenue dans une éprouvette graduée de 1 L.

-  On obtient le fichier : bille50

-  Données :

-  Propriétés du clip :

 

 

b)-  Exploitation :

-  Tableau de valeurs :

-  Graphe 1 : v = f (t).

 

-  Dans un premier temps, la vitesse de la bille augmente au cours du temps, son énergie cinétique augmente aussi alors que l’énergie potentielle de pesanteur diminue.

-  Dans un deuxième temps, la vitesse de la bille se stabilise pour atteindre une valeur limite :

-  v_lim ≈ 0,94 m / s

-  De même, son énergie cinétique se stabilise, alors que l’énergie potentielle de pesanteur diminue toujours.

-  Tableau de valeurs :

-  Graphe 2 : E = f (t).

 

-  On remarque qu’au cours de la chute de la bille :

-   L’énergie cinétique du système augmente puis se stabilise.

-   L’énergie potentielle de pesanteur diminue.

-  L’énergie mécanique du système diminue aussi.

-  En conséquence, l’énergie mécanique de la bille ne se conserve pas.

 Conclusions :

-  Un solide en chute dans un fluide est soumis à des frottements exercés par le fluide.

-  Son énergie mécanique diminue au cours de la chute.

-  De l’énergie est transférée de la bille vers le fluide.

-  Le système S est soumis aux forces suivantes :

 Lorsqu’un système est soumis à des forces non conservatives qui travaillent, son énergie mécanique E_m ne se conserve pas.

-  Sa variation est égale au travail des forces non conservatives.

-   

-  Dans le cas présent, le travail de la force de frottement est résistant, l’énergie mécanique diminue au cours du mouvement du système.

-  Lorsqu’il y a non-conservation de l’énergie mécanique, il y a transfert partiel de l’énergie potentielle en énergie cinétique ou inversement.

III- Applications.

1)- Étude énergétique du pendule simple.

a)-  Présentation.

-  Un pendule simple est constitué d’un objet sphérique de masse m suspendu à un fil inextensible de longueur ℓ.

-  Remarque : la masse du fil est négligeable devant celle de l’objet.

-  La longueur ℓ est grande devant celle de l’objet.

-  Dans le cas contraire, on dit que le pendule est pesant.

 

b)-  Tension du fil.

  Étude à l’équilibre :

-  Exprimer la valeur de la tension T exercée par le fil sur l’objet de masse m.

-  A l’équilibre, le solide de masse m est soumis à des forces dont les effets se compensent.

-  Le centre d’inertie du solide est immobile, la réciproque du principe de l’inertie permet d’écrire que :

-   

  étude lorsque le solide est en mouvement.

-  On écarte le solide de sa position d’équilibre d’un angle θ₀ < 10°.

-  On laisse le pendule osciller librement et on fait une représentation à un instant t quelconque.

    

 

-  Expression de la valeur de la tension T en fonction de θ, v, m et g à l’instant t.

-  On travaille dans le repère de Frenet :

-  On donne les coordonnées de chaque vecteur force dans ce repère :

-   

-  La deuxième loi de Newton permet d’écrire :

-   

  étude énergétique.

-  Considérons le système : S : objet de masse m considéré comme ponctuel.

-  On néglige dans un premier temps les forces de frottements.

► énergie cinétique :

-  dans le référentiel terrestre le système S se déplace à la vitesse v :

-   

► Énergie potentielle :

-  L’altitude du centre d’inertie de l’objet varie au cours du temps.

-  L’énergie potentielle de pesanteur du système S varie au cours du temps :

-  E_P = m . g . z + cte.

-  En adoptant comme niveau de référence, le plan horizontal contenant la position d’équilibre du point G de l’objet z_E = 0 :

-  E_P = m . g . z

-  Travaux des forces sur le chemin M₀E :

 

-  Travail de la tension  pour passer de M₀ à E : il est nul

-  car la force  est perpendiculaire au déplacement.

-  Travail du poids pour passer de M₀ à E :

-   

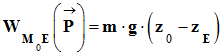
-  Le poids est une force conservative.

 

 

-  Les forces de frottements sont négligeables dans les conditions de l’expérience.

-  L’énergie mécanique d’un système S soumis à des forces conservatives est constante, elle se conserve.

-  Au cours du mouvement, la variation de l’énergie mécanique : ΔE_m = 0

-  ΔE_C + ΔE_P = 0  =>  ΔE_C = – ΔE_P

-  Lorsqu’il y a conservation de l’énergie mécanique, il y a transfert total de l’énergie potentielle en énergie cinétique.

-  Autre expression de l’énergie potentielle de pesanteur :

 

-   

-  Expression de l’énergie mécanique :

-   

-  Son énergie mécanique se conserve, elle reste constante.

-  E_m = E_P + E_C = cte

► Représentation graphique :

-  Données :

 

 

2)- Étude énergétique du pendule simple amorti (amortissement fluide).

► Représentation graphique :

-  Données :

 

 

-  Dans le cas présent, le travail de la force de frottement est résistant, l’énergie mécanique diminue au cours du mouvement du système.

-  Lorsqu’il y a non-conservation de l’énergie mécanique, il y a transfert partiel de l’énergie potentielle en énergie cinétique ou inversement.

-  Lorsqu’un système est soumis à des forces non conservatives qui travaillent, son énergie mécanique E_m ne se conserve pas.

-  Sa variation est égale au travail des forces non conservatives.

-   

-  Calculer le travail effectué par la force de frottement lors de la première seconde du mouvement.

-  Au temps t = 0 s, le pendule est écarté de sa position d’équilibre d’un angle de 4 ° et il est lâché sans vitesse initiale.

-  Il possède de l’énergie potentielle de pesanteur :

-  ΔE_m = – 2,5 × 10^–3 J

-  Le travail de la force de frottement est négatif, il est résistant.

-  La force de frottement s’oppose au déplacement.

-   

3)- QCM :  QCM sous forme de tableau.   QCM réalisé avec le logiciel Questy (Pour s'auto-évaluer)

 

4)- Exercices :  Exercices : Énoncé et correction

a)-  Exercice 9 page 199 : Calculer le travail d’une force constante.

b)-  Exercice 10 page 199 : Calculer le travail d’une force électrostatique.

c)-  Exercice 12 page 199 : Identifier les différentes formes d’énergie.

d)-  Exercice 13 page 199 : Utiliser les transferts d’énergie pour calculer une vitesse.

e)-  Exercice 18 page 200 : Utiliser la non-conservation de l’énergie mécanique.

f)-  Exercice 24 page 202 : Service au tennis.

g)-  Exercice 27 page 203 : Le pendule de Foucault.

h)-  Exercice 28 page 204 : Les dominos.