|
|
La lumière : un flux de photons Exercices |
|
|
|
|
|
QCM r
La lumière : un flux
de photons Effet photoélectrique L’absorption ou
l’émission de photons |
1)- Exercice 03 page 416 : Connaître l’effet photoélectrique :
|
Connaître l’effet photoélectrique :
-
Définir l’effet photoélectrique.
-
Illustrer la réponse à l’aide d’un
schéma légendé.
|
|
Connaître l’effet photoélectrique :
-
Définition de l’effet
photoélectrique :
-
L’effet photoélectrique est le
phénomène d’éjection d’électrons d’un métal sous l’effet de
radiations lumineuses de fréquence
υ. - Pour un métal donné, l’effet photoélectrique se produit lorsque la longueur d’onde de la radiation mise en jeu est inférieure à une longueur d’onde de seuil λS. - Alors, La fréquence
ν de la radiation est supérieure à la fréquence de seuil
νS. - L’énergie de chaque photon associé à cette radiation lumineuse est alors suffisante pour arracher un électron du métal, - Elle est supérieure au travail d’extraction d’un électron du métal Wextraction. - L’énergie excédentaire est
emportée par l’électron sous forme d’énergie cinétique.
-
Schéma :
-
Équation de conservation de
l’énergie : Équation d’EINSTEIN de l’effet photoélectrique :
|
||||||||||||
2)- Exercice 05 Page 416 : Interpréter l’effet photoélectrique :
|
En 1888, Wilhelm HALLWACHS observe qu’une radiation de longueur d’onde λ1 = 330 nm est capable de charger positivement une plaque de zinc, ce que ne permet pas
une radiation de longueur d’onde λ2 = 400 nm. 1.
Expliquer pourquoi la plaque de zinc se
charge positivement. 2.
Calculer l’énergie des photons associés à
chacune des radiations évoquées. 3. Proposer une explication à la constatation de Wilhelm HALLWACHS selon laquelle la radiation de longueur d’onde λ2 = 400 nm
ne permet pas à la plaque de zinc de se charger positivement.
-
Donnée :
-
Constante de Planck : h = 6,63
× 10–34 J . s
-
c = 3,00 × 108 m .
s – 1 |
|
Interpréter l’effet photoélectrique : 1.
La plaque de zinc se charge positivement.
-
Pour la radiation de longueur d’onde
λ1 = 330 nm,
il se produit l’effet photoélectrique.
-
L’effet photoélectrique est le
phénomène d’éjection d’électrons d’un métal sous l’effet de
radiations lumineuses de fréquence
υ.
-
La plaque présente alors un défaut
d’électrons et elle est de ce fait chargée positivement. 2.
Énergie des photons associés à chacune des
radiations évoquées.
-
Relation de PLANCK-EINSTEIN :
-
Énergie des photons de longueur
d’onde λ1 =
330 nm :
-
-
Énergie des photons de longueur
d’onde λ2 =
400 nm :
-
-
Tableau de valeurs :
►
Remarque :
-
Plus la longueur d’onde associée au
photon est grande est plus l’énergie qu’il transporte est petite.
-
Plus la longueur d’onde est grande et
plus la fréquence du photon est petite.
-
Plus la fréquence du photon est
grande et plus l’énergie associée au photon est grande. 3.
Une explication à la constatation de Wilhelm
HALLWACHS. - Pour un métal donné, l’effet photoélectrique se produit lorsque la longueur d’onde de la radiation mise en jeu est
inférieure à une longueur d’onde de seuil
λS.
-
Ou lorsque la fréquence
ν de cette radiation est supérieure à la fréquence de seuil
νS. - La radiation de longueur d’onde λ2 = 400 nm ne permet pas à la plaque de zinc de se charger positivement
car
l’énergie transportée par les photons n’est pas suffisante pour
arracher des électrons au métal.
-
Le phénomène photoélectrique ne se
produit pas pour cette longueur d’onde
λ2 = 400 nm.
-
La plaque ne se charge pas
positivement. |
||||||||||||||||||||||||
3)- Exercice 07 page 416 : Réaliser un bilan d’énergie :
|
Réaliser un bilan d’énergie : Un photon d’énergie Ephoton = 5,03 eV extrait,
par effet photoélectrique, des électrons à un morceau de fer
métallique. 1. Écrire la relation entre l’énergie du photon incident Ephoton, le travail d’extraction Wextraction et l’énergie maximale ECmax d’un électron extrait. 2.
Calculer, en joule, l’énergie cinétique
maximale de l’électron arraché.
-
Données :
-
Constante de Planck : h = 6,63
× 10–34 J . s
-
c = 3,00 × 108 m .
s – 1
-
1 eV = 1,60 × 10–19 J
-
Pour le fer :
Wextraction = 4,67 eV.
-
Masse de l’électron :
-
me = 9,109 × 10–31
kg |
Réaliser un bilan d’énergie : 1.
Relation entre l’énergie du photon incident
Ephoton, le travail d’extraction Wextraction
et l’énergie maximale ECmax d’un électron extrait.
-
Équation d’EINSTEIN de l’effet
photoélectrique : ℰphoton
= Wextraction + ℰCmax
υphoton La
fréquence du photon en hertz (Hz)
Wextraction
Travail d’extraction en joule (J) ou électron-volt (eV) 1
eV = 1,60 × 10–19 J
me
Masse de l’électron me = 9,109 × 10–31
kg
vmax
Vitesse maximale de l’électron en
mètre par seconde (m . s–1)
h
Constante de Planck :
h
= 6,626 × 10–34 J . s 2.
Énergie
cinétique maximale de l’électron arraché.
-
Ephoton = 5,03
eV
-
Wextraction =
4,67 eV
-
ℰphoton = Wextraction
+ ℰCmax
-
ℰCmax = ℰphoton
– Wextraction
-
ℰCmax =
5,03 –
4,67
-
ℰCmax ≈ 0,360 eV
-
ℰCmax ≈ 5,76
× 10–20 J
-
Vitesse maximale d’extraction de
l’électron arraché :
-
-
Fréquence de la radiation :
-
Ephoton = 5,03
eV
-
-
Longueur d’onde dans le vide de la
radiation :
-
-
La radiation appartient au domaine
des UV.
![]()
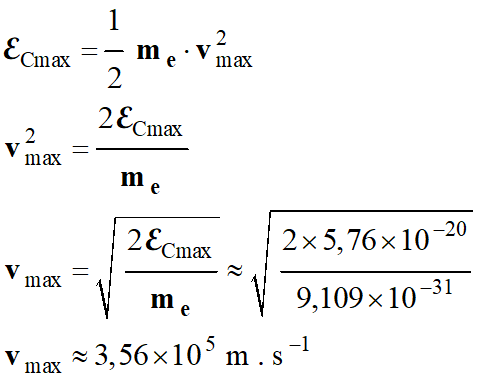
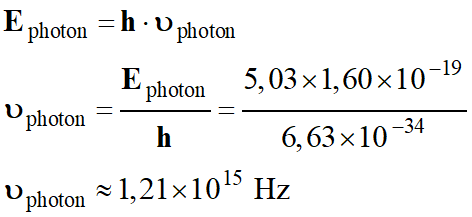
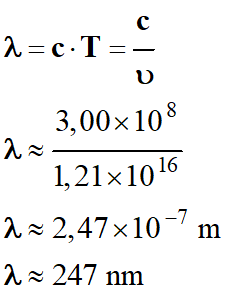
![]()
4)-Exercice 09 page 417 : Calculer des rendements :
|
Calculer des rendements : Le graphique ci-dessous représente la puissance électrique disponible d’un panneau de cellules photovoltaïques de 1,1 m2 pour différents éclairements E. 1.
Comment la puissance électrique disponible
évolue-t-elle lorsque l’éclairement E diminue ? 2.
Rappeler l’expression du rendement η
pour un panneau de cellules photovoltaïques. 3.
Calculer le rendement maximal pour les
différents éclairements, puis conclure.
|
Calculer des rendements : 1.
Évolution de la puissance électrique
disponible en fonction de l’éclairement E :
-
Lorsque l’éclairement augmente, la
puissance électrique disponible augmente. 2.
Expression du rendement η pour un
panneau de cellules photovoltaïques.
►
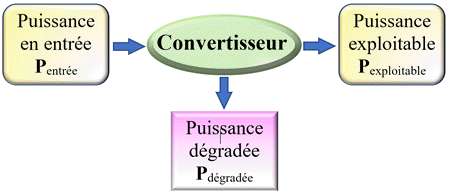
Rendement d’un convertisseur :
-
Le rendement
η d’un convertisseur est le rapport de la puissance exploitable sur
la puissance en entrée.
η
Grandeur sans unité : 0
< η < 1
Pexploitable
Puissance exploitable en watt (W)
Pentrée
Puissance en entrée en watt (W)
►
Rendement d’une cellule
photovoltaïque :
-
Avec les notations précédentes :
η
Grandeur sans unité : 0
< η < 1
Pélec
Puissance exploitable : Puissance électrique disponible
en watt (W)
Plum
Puissance en entrée : Puissance lumineuse en watt (W)
-
Le rendement
η d’une cellule photovoltaïque est le rapport de la puissance
exploitable sur la puissance en entrée.
-
Le rendement
η d’une cellule photovoltaïque est le rapport de la puissance
électrique disponible Pélec sur la puissance
lumineuse Plum.
-
Remarque :
la puissance lumineuse : Plum
= E . S
Plum
Puissance en entrée : Puissance lumineuse en watt (W)
E
Éclairement en watt par mètre carré (W . m–2)
S
Surface de la zone éclairée en mètre carré (m2) 3.
Rendement
maximal pour les différents éclairements.
-
Exploitation graphique :
-
Rendement maximal pour
E = 1000 W . m–2
-
Puissance lumineuse reçue par le
panneau :
-
Plum =
E . S = 1000 × 1,1
-
Plum ≈ 1,1 × 103
W
-
Puissance électrique maximale
disponible :
-
Pélec max ≈ 104 W
-
Rendement maximal :
-
-
Rendement maximal pour
E = 600 W . m–2
-
Puissance lumineuse reçue par le
panneau :
-
Plum =
E . S = 600 × 1,1
-
Plum ≈ 6,6 × 102
W
-
Puissance électrique maximale
disponible :
-
Pélec max ≈ 62 W
-
Rendement maximal :
-
-
Rendement maximal pour
E = 200 W . m–2
-
Puissance lumineuse reçue par le
panneau :
-
Plum =
E . S = 200 × 1,1
-
Plum ≈ 2,2 × 102
W
-
Puissance électrique maximale
disponible :
-
Pélec max ≈ 20 W
-
Rendement maximal :
-
-
Le rendement maximal est sensiblement le même
dans les trois cas.
-
Il est voisin de 11 %.
-
Le rendement maximal ne dépend pratiquement pas de
l’éclairement E du
panneau photovoltaïque.
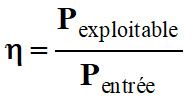

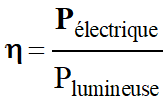 ou
ou
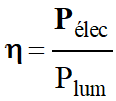
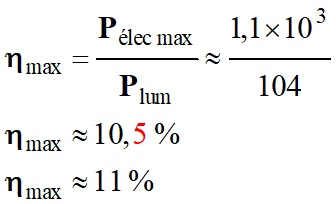
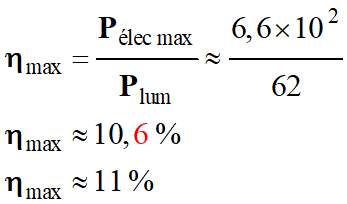
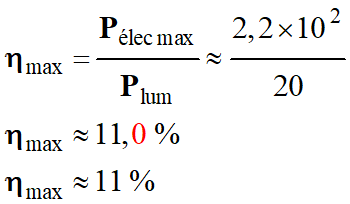
![]()
5)- Exercice 13 page 417 : Conservation de l’énergie :
|
Conservation de l’énergie : Le graphique ci-dessous représente l’énergie cinétique maximale des électrons émis d’une plaque de zinc par effet photoélectrique, en fonction de la fréquence υ de la radiation incidente. 1.
: a.
Calculer la longueur d’onde seuil λS
permettant d’obtenir l’effet photoélectrique avec le zinc. b.
La grandeur λS
correspond-elle à une longueur d’onde minimale ou maximale
d’obtention de l’effet photoélectrique ?
2.
Pour une radiation de fréquence υ =
1,1 × 1015 Hz, calculer, à l’aide d’un bilan d’énergie,
l’énergie cinétique maximale des électrons émis. 3.
Vérifier graphiquement le calcul précédent.
-
Données :
-
Constante de Planck : h = 6,63
× 10–34 J . s
-
c = 3,00 × 108 m .
s – 1
-
1 eV = 1,60 × 10–19 J
-
Masse de l’électron :
-
me = 9,109 × 10–31
kg
|
|
Conservation de l’énergie : Graphique : 1.
: a.
Longueur d’onde seuil λS
permettant d’obtenir l’effet photoélectrique avec le zinc.
-
Exploitation graphique :
-
À partir du graphique, on peut
déterminer la valeur de la fréquence seuil pour la plaque de zinc :
-
υS ≈ 8,8 × 1014
Hz
-
On en déduit la valeur de la longueur
d’onde seuil à partir de la relation fondamentale :
-
Dans le cas présent :
-
-
La longueur d’onde seuil vaut environ
340 nm.
-
La radiation appartient au domaine
des UV. b.
Étude de la longueur d’onde seuil λS
-
Pour que l’effet photoélectrique se
produise, il faut que la fréquence des électrons soit supérieure la
fréquence seuil υS.
-
Comme
-
Il faut que la longueur d’onde, du
photon incident, soit inférieure à la longueur d’onde seuil
λS.
-
C’est la longueur d’onde maximale
au-delà de laquelle il n’est pas possible d’arracher les électrons
libres du métal. - Si λ > λS. alors υ < υS et l’énergie transportée par le photon (E = h . υ < h . υS) est inférieure à l’énergie minimale
permettant
d’arracher un électron libre à la surface du zinc. 2.
Énergie cinétique maximale des électrons
émis.
-
Pour une radiation de fréquence
υ = 1,1 × 1015
Hz :
-
Équation d’EINSTEIN de l’effet
photoélectrique :
- L’énergie minimale qui permet d’arracher un électron d’un métal est égale au travail à fournir pour
extraire un électron libre proche de la surface du métal.
-
Cette énergie est appelée travail
d’extraction, notée Wextraction.
-
Wextraction =
h .
υS
-
Bilan d’énergie :
-
ℰphoton = Wextraction
+ ℰCmax
-
ℰCmax = ℰphoton
– Wextraction
-
ℰCmax =
h . υ –
h .
υS
-
ℰCmax =
h . (υ –
υS)
-
Application numérique :
-
ℰCmax =
h . (υ –
υS)
-
ℰCmax = 6,63 × 10–34
× (1,1 × 1015 – 8,8 × 1014)
-
ℰCmax ≈ 1,458
× 10–19 J
-
ℰCmax ≈ 1,5 × 10–19
J
-
ℰCmax ≈ 0,91 eV 3.
Vérification graphique.
-
Exploitation graphique :
-
Graphiquement :
-
ℰCmax ≈ 0,90 eV
-
Cette valeur est en accord avec celle
trouvée précédemment.
-
Étude de la courbe : ℰCmax
= f (υ)
-
Pour
υ ≥
υS , on
obtient une fonction affine du type : ℰCmax =
a . υ +
b
-
Or le bilan énergétique donne :
-
ℰphoton = Wextraction
+ ℰCmax
-
ℰCmax = ℰphoton
– Wextraction
-
ℰCmax =
h . υ – Wextraction
-
En identifiant :
-
Il vient :
-
a =
h et
b = – Wextraction
-
Détermination du coefficient
directeur de la droite tracée :
-
Exploitation graphique :
-
-
Graphiquement :
h ≈ 6,7 × 10–34
J . s
-
Incertitude relative :
-
-
Le résultat est correct. |
|||||||||||||||||
6)- Exercice 15 page 418 : Énergie cinétique des électrons :
|
Énergie cinétique des électrons : Afin de déterminer l’énergie cinétique des électrons arrachés d’un métal par effet photoélectrique, le physicien Philipp LENARD
utilisait un dispositif expérimental dont le principe est schématisé
ci-dessous : Une tension électrique est appliquée entre le métal et le
collecteur. Il apparaît alors un champ électrique qui empêche les électrons
de rejoindre le collecteur. La tension nécessaire, pour que l’intensité du courant électrique soit nulle, est appelée tension d’arrêt. Elle est notée Ua. L’énergie cinétique maximale des électrons émis par effet
photoélectrique se calcule alors avec la relation : ℰCmax =
e × Ua. Avec ℰCmax
en joule (J), e en coulomb (C) et Ua en
volt (V). Une plaque métallique en cuivre est illuminée par une radiation
de longueur d’onde λ. Dans le cas particulier d’une radiation ultraviolette telle que λ = 171 nm, on trouve la tension d’arrêt : Ua = 2,80
V. 1.
: a.
Calculer l’énergie cinétique maximale
ℰCmax acquise
par les électrons. b.
En déduire la valeur de la vitesse maximale
vmax des
électrons émis par effet photoélectrique. 2.
Rappeler la relation traduisant la
conservation d’énergie dans le cas de l’effet photoélectrique. 3.
Calculer le travail d’extraction Wextraction
d’un électron pour le cuivre. 4.
Observe-t-on l’effet photoélectrique pour le
cuivre si on l’illumine avec une radiation de longueur d’onde λ
= 350 nm.
-
Donnée :
-
Constante de Planck : h = 6,63
× 10–34 J . s
-
c = 3,00 × 108 m .
s – 1
-
1 eV = 1,60 × 10–19 J
-
Masse de l’électron :
-
me = 9,11 × 10–31
kg |
|
Énergie cinétique des électrons : 1.
: a.
Énergie cinétique maximale
ℰCmax acquise par les électrons.
-
Radiation ultraviolette : λ =
171 nm
-
Tension d’arrêt : Ua = 2,80
V
-
Relation :
-
ℰCmax = e ×
Ua.
-
ℰCmax = 1,60 × 10–19
× 2,80
-
ℰCmax = 2,80 eV
-
ℰCmax ≈ 4,48 × 10–19
J b.
Valeur de la vitesse maximale
vmax des électrons émis par effet photoélectrique.
-
Relation :
-
2.
Relation traduisant la conservation
d’énergie dans le cas de l’effet photoélectrique.
-
Équation d’EINSTEIN de l’effet
photoélectrique :
3.
Valeur du travail d’extraction Wextraction
d’un électron pour le cuivre. ℰphoton = Wextraction
+ ℰCmax
►
Travail d’extraction : Wextraction.
-
L'énergie minimale qui permet
d’arracher un électron d’un métal est égale au travail à fournir
pour extraire un électron libre proche de la surface du métal.
-
Cette énergie est appelée travail
d’extraction, notée Wextraction.
-
Pour un métal donné, l’effet
photoélectrique se produit lorsque la longueur d’onde de la
radiation mise en jeu est inférieure à une longueur d’onde de seuil
λS.
-
La fréquence ν de cette
radiation est supérieure à la fréquence de seuil νS. - L’énergie de chaque photon associé à cette radiation lumineuse est alors suffisante pour arracher un électron du métal :
- On observe alors l’effet photoélectrique.
-
Wextraction = h
. υS
-
ℰphoton = Wextraction
+ ℰCmax
-
Wextraction = ℰphoton
– ℰCmax
-
Wextraction = h
. υ – e × Ua
-
Comme
-
►
Remarque :
-
Les tables donnent pour le travail
d’extraction dans le cas du cuivre :
-
Wextraction = 4,71
eV ou Wextraction = 7,53 × 10–19 J
-
On a l’ordre de grandeur, mais la
valeur trouvée est un peu faible.
-
Fréquence et longueur d’onde de seuil
dans le cas du cuivre :
-
Wextraction = h
. υS
-
-
Longueur d’onde de seuil :
-
►
Remarque :
-
Les tables donnent :
-
λS ≈ 263 nm et
υS ≈ 1,14 × 1015
Hz 4.
Effet photoélectrique pour le cuivre et
radiation de longueur d’onde λ = 350 nm.
-
Dans le cas présent,
λ > λS
-
Il découle de ceci que
υ < υS
-
Si λ > λS.
alors υ < υS et l’énergie transportée par
le photon (E = h . υ < h . υS)
est inférieure à l’énergie minimale permettant d’arracher un
électron libre à la surface du cuivre.
-
L’effet photoélectrique ne se produit
pas.
►
Remarque :
-
On peut refaire tous les calculs en
prenant comme tension d’arrêt :
-
Ua = 2,56 V
-
Ainsi, on obtiendra les valeurs
données par les tables. |
||||||||||||
7)- Exercice 17 page 419 : Comparaison de l’effet photovoltaïque :
|
Comparaison de l’effet photovoltaïque : Voici, pour divers métaux, l’énergie cinétique maximale ℰCmax d’électrons arrachés par effet photoélectrique en fonction de la fréquence υ de la radiation
d’éclairement. 1.
Pour quel(s) métal (métaux), l’effet
photoélectrique se produit-il avec des radiations lumineuses dans le
domaine du visible. 2.
: a.
Établir, par un bilan d’énergie,
l’expression de l’énergie cinétique maximale des électrons en
fonction de la fréquence de la radiation incidente. b.
Expliquer pourquoi les différentes courbes
sont des droites qui ont le même coefficient directeur et des
ordonnées à l’origine différentes. c.
Exploiter ces courbes pour déterminer la
constante de Planck h et le travail d’extraction Wextraction
d’un électron pour chacun des métaux.
-
Données :
-
Constante de Planck :
h = 6,63 × 10–34
J . s
-
c = 3,00 × 108
m . s–1
-
1 eV = 1,60 × 10–19 J
-
Masse de l’électron :
-
me = 9,11 × 10–31
kg |
|
Comparaison de
l’effet photovoltaïque :
1.
Effet
photoélectrique et domaine du visible.
-
Exploitation du graphique :
-
À partir
du graphique, on peut déterminer la fréquence de seuil de chaque
métal :
-
Pour le
potassium : υS ≈ 5,60 × 1014 Hz
-
-
Cette
radiation se situe dans le domaine du visible :
-
Pour le
béryllium : υS ≈ 12,0 × 1014 Hz
-
-
La
radiation appartient au domaine des
UV.
-
Pour le
béryllium : υS ≈ 13,8 × 1014 Hz
-
-
La radiation appartient au domaine des
UV.
2.
:
a.
Énergie cinétique
maximale des électrons en fonction de la fréquence de la radiation
incidente.
-
Équation
d’EINSTEIN de l’effet photoélectrique :
-
Bilan
d’énergie :
-
ℰphoton
= Wextraction
+ ℰCmax
-
ℰCmax
= ℰphoton – Wextraction
-
Étude de
la courbe : ℰCmax
= f (υ)
-
Pour
υ ≥
υS , on obtient une fonction affine du type :
ℰCmax =
a . υ +
b
-
Or le
bilan énergétique donne :
-
ℰphoton
= Wextraction
+ ℰCmax
-
ℰCmax
= ℰphoton – Wextraction
-
ℰCmax
= h . υ –
Wextraction
-
Le travail d’extraction
Wextraction
est une grandeur caractéristique du métal.
b.
Coefficient
directeur et ordonnées à l’origine des différentes courbes.
-
Exploitation graphique :
-
-
Les trois
droites sont parallèles.
-
Tracé du
graphique avec Excel :
-
L’ordonnée à l’origine donne la valeur opposée au
travail d’extraction Wextraction.
c.
Constante de
Planck h et le travail d’extraction Wextraction
d’un électron pour chacun des métaux.
-
Graphiquement :
-
En
identifiant :
-
Il vient :
-
a
= h et b = –
Wextraction
-
h = a
≈ 6,7 × 10–34 J . s
-
Incertitude relative :
-
-
Tracé du
graphique avec Excel :
-
L’ordonnée
à l’origine donne la valeur opposée au travail d’extraction
Wextraction.
-
Pour le
potassium :
-
Wextraction
≈ 2,3 eV
-
Pour le
béryllium :
-
Wextraction
≈ 5,0 eV
-
Pour le
platine :
-
Wextraction
≈ 5,7 eV
-
Valeurs
données par les tables :
|
||||||||||||||||||||
|
|