|
|
La lunette astronomique Exercices |
|
|
|
|
|
QCM r
La lunette astronomique. Construction du faisceau
traversant une lunette afocale. |
1)- Exercice 02 page 396 : Reconnaitre la schématisation d’une lunette afocale :
|
Quelle est la schématisation correcte d’une lunette afocale parmi
celles-ci-dessous ? Justifier votre choix. a.
b.
c.
|
|
Schéma correct d’une lunette afocale :
-
Une lunette est afocale lorsque le
foyer principal image de l’objectif coïncide avec le foyer principal objet de
l’oculaire.
►
Le schéma correct est le schéma
a.
-
Les foyers objet
F2 et image F’1
sont confondus.
-
L’image
A’’B’’
se trouve à l’infini et un œil normal peut observer cette image sans
accommoder.
-
Dans ce cas, la lumière traverse
l’objectif, puis l’oculaire
►
Le schéma ne
b. ne convient pas. La lunette n’est pas afocale.
-
L’image ne se forme pas à l’infini.
-
L’œil doit accommoder pour observer
l’image A’’B’’.
►
Pour le schéma c., l’objectif
et l’oculaire sont inversés.
-
Dans ce cas, la lumière traverse
l’oculaire, puis l’objectif.
-
Ce schéma ne convient pas. |
2)- Exercice 04 page 396 : Identifier un faisceau lumineux :
|
Identifier un faisceau lumineux : 1. Quelle est la schématisation représentant correctement le faisceau lumineux issu d’un point B situé à l’infini et qui éclaire une lentille
mince convergente parmi les propositions ci-dessous ? Justifier
votre choix. a.
b.
c.
|
|
Identifier un faisceau lumineux : 1.
Schématisation du faisceau lumineux issu
d’un point B situé à l’infini : a.
La bonne configuration est la b.
-
Les rayons provenant du point
B situé à l’infini sont
parallèles.
-
Tracé :
-
On trace le plan focal image
(perpendiculaire à Δ
issue de F’1).
-
On trace le rayon lumineux parallèle
au rayon 1 passant par le
centre optique.
-
Ce rayon n’est pas dévié. Il vient
couper le plan focal image au point
H.
-
Les rayons qui émergent des bords de
la lentille viennent converger au point
H.
-
Le rayon parallèle au rayon 1 passant par le foyer image
F1 émerge de la lentille parallèlement à l’axe optique. |
3)- Exercice 06 page 397 : Représenter le faisceau émergeant d’une lentille afocale :
|
Représenter le faisceau émergeant d’une lentille afocale : On a schématisé ci-dessous une lunette astronomique afocale
modélisée par deux lentilles minces convergentes. On a représenté le faisceau lumineux issu d’un point objet
B situé à l’infini éclairant l’objectif de la
lunette. Schéma :
-
Reproduire le schéma et représenter
le faisceau émergent issu du point B après traversée de
cette lunette. |
Représenter le faisceau émergeant d’une lentille afocale :
-
Schéma de la situation :
![]()
4)- Exercice 09 page 397 : Tracer l’image d’un objet situé à l’infini.
|
Tracer l’image d’un objet situé à l’infini : On a représenté, sur le schéma ci-dessous, l’image A1B1 d’un objet AB situé à l’infini donnée par l’objectif d’une lunette afocale. A1B1
devient un objet pour l’oculaire. Reproduire le schéma et le compléter avec les deux rayons
émergeant de l’oculaire. |
Tracer l’image d’un objet situé à l’infini :
-
Schéma complété avec les deux rayons
émergeant de l’oculaire :
-
L’angle
θ = 10 ° pour que le
tracé soit plus facile.
-
Le rayon rouge qui est parallèle à
l’axe optique émerge de l’oculaire en passant par le foyer image
F’2.
-
Le rayon bleu émerge de l’oculaire
parallèlement au rayon rouge.
![]()
5)- Exercice 11 page 398 : Établir le grossissement d’une lunette afocale :
|
Établir le grossissement d’une lunette afocale On a représenté ci-dessous le schéma d’une lentille afocale. 1.
Justifier que 2.
Exprimer tan θ’ en fonction de A1B1
et O2F2. 3.
Les angles θ et θ’ étant
petits, exprimer le grossissement G en fonction de f’1
et f’2. |
|
Établir le grossissement d’une lunette afocale 1.
Justification que
-
Considérons le triangle
O1A1B1
rectangle en A1 : ZOOM
-
Les points
F2,
F’1 et
A1 sont
confondus.
-
2.
Expression de tan θ’ en fonction de
A1B1 et O2F2.
-
Considérons le triangle
O2A1B1
rectangle en A1 :
-
Les points
F2,
F’1 et
A1 sont
confondus.
-
3.
Expression du grossissement G en
fonction de f’1 et f’2.
-
Les angles
θ et
θ’ étant petits,
-
tan
θ ≈
θ et tan θ’ ≈
θ’
-
Définition du grossissement :
-
Le grossissement d’une lunette est le
rapport entre :
-
L’angle
θ sous lequel l’objet est
vu à l’œil nu et
-
L’angle
θ’ sous lequel son image est vue à
travers la lunette.
-
Ainsi l’objet éloigné (B ∞) est vu sous l’angle
θ
et l’image A’B’ est vue sous l’angle
θ’.
-
Le grossissement
G d’une lunette est donné par la relation suivante :
-
Avec l’approximation précédente :
-
-
On obtient la relation suivante :
-
-
-
Quelques valeurs :
-
Pour des raisons de commodité pour le tracé, on a
pris pour angle θ = 8,0 °
-
Grossissement :
-
-
D’autre part, pour les petits
angles :
-
-
Dans ce cas, on ne peut pas faire
l’approximation des petits angles.
-
Maintenant, si on prend comme angle
θ = 2,0 °
-
Alors :
-
A1B1
= f’1 × tan θ
-
A1B1
= 8,0 × tan 2,0
-
A1B1
≈ 0,28 cm
-
Calcul de
θ’
-
-
Grossissement :
-
-
Dans ce cas, on peut faire
l’approximation des petits angles. |
||||||||||
6)- Exercice 15 page 398 :Trajet d’un faisceau lumineux :
|
Trajet d’un faisceau lumineux : On a représenté ci-dessous un faisceau lumineux délimité par deux rayons issus d’un point objet B situé à l’infini. Ces rayons arrivent sur une lentille mince convergente
modélisant l’objectif d’une lunette astronomique afocale. L’objectif a une distance focale f’1 = 20 cm et
la lentille oculaire, non représentée, a une distance focale f’2 = 5,0
cm. 1.
Reproduire le schéma de cette lunette
astronomique afocale en prenant l’échelle 1,0 cm sur le schéma pour
5,0 cm dans la réalité. 2.
Où le point B est-il situé ? 3.
: a.
Où l’image intermédiaire B1
du point B à travers l’objectif de la lunette se
forme-t-elle ? b. Le plan perpendiculaire à l’axe optique qui contient B1 est le plan focal image de l’objectif et également le plan focal objet de l’oculaire. Justifier l’expression « plan
focal ». 4.
Tracer le trajet du faisceau lumineux entre
la lentille et l’oculaire. 5.
: a.
Où l’image finale B’ de B1
donnée par l’oculaire se forme -t-elle ? b.
Comment les rayons émergent-ils de
l’oculaire ? c.
Prolonger le faisceau émergeant de la
lunette astronomique ? |
|
Trajet d’un faisceau lumineux :
L’objectif a une distance focale f’1 = 20 cm et
la lentille oculaire, non représentée, a une distance focale f’2 = 5,0
cm.
-
Remarque : pour que le tracé soit
plus facile, on choisit comme diamètre apparent de l’objet
B situé à l’infini : θ =
5,0 ° 1.
Schéma de cette lunette astronomique
afocale.
-
Échelle : 1,0 cm sur le schéma pour
2,5 cm dans la réalité : 2.
Position du point B
-
Énoncé : « On a représenté ci-dessous
un faisceau lumineux délimité par deux rayons issus d’un point objet
B situé à l’infini ».
-
Le point
B est situé à l’infini (B
∞). 3.
: a.
Position de l’image intermédiaire B1
du point B à travers l’objectif :
-
Comme le point
B est situé à l’infini, l’image
B1 se forme dans le plan focal image.
-
C’est le point d’intersection du
rayon parallèle au rayon incident passant par le centre optique
O1 et le plan focal image
P1.
-
Plan focal image : Plan
perpendiculaire à l’axe optique contenant le foyer image
F’1.
-
La distance
O1A1
= f’1 = 20 cm
-
Schéma : b.
Expression « plan focal ».
-
Le plan perpendiculaire à l’axe
optique qui contient B1
est le plan focal image de l’objectif et également le plan focal
objet de l’oculaire.
-
On distingue le plan focal image et
le plan focal objet.
-
Pour l’objectif :
-
Plan focal objet : Plan
perpendiculaire à l’axe optique contenant le foyer objet
F1.
-
Plan focal image : Plan
perpendiculaire à l’axe optique contenant le foyer image
F’1.
-
Tout faisceau parallèle arrivant sur
la lentille convergente, converge en un point du plan focal image. 4.
Trajet du faisceau lumineux entre la
lentille et l’oculaire.
-
Schéma : 5.
: a.
Position de l’image finale B’ de B1
donnée par l’oculaire :
-
Schéma :
-
L’image de forme à l’infini.
-
Elle est virtuelle et l’œil peut
observer sans accommoder. b.
Rayons émergeant de l’oculaire :
-
Schéma : c.
Faisceau émergeant de la lunette
astronomique :
-
Le faisceau émergeant de la lunette
astronomique est un faisceau de rayons parallèles.
-
Les différentes valeurs :
|
7)- Exercice 16 page 399 : Lunette de laboratoire :
|
Lunette de laboratoire : On réalise une maquette d’une lunette astronomique afocale à
l’aide de deux lentilles convergentes L1 et L2
afin d’observer la Lune.
On choisit deux points A et B diamétralement
opposés, l’objet AB ainsi défini est considéré à l’infini. On a représenté, sur le schéma à l’échelle ci-dessous, les deux
lentilles, ainsi que l’image intermédiaire A1B1
de la Lune donnée par l’objectif. 1.
Reproduire la figure sur papier millimétré
et tracer le trajet de deux rayons issus du point objet B. 2.
Représenter sur la figure l’angle θ
sous lequel on voit la Lune à l’œil nu. Le calculer. 3.
Calculer la distance Terre-Lune sachant que
le diamètre de la Lune est D = 3,47 × 103 km. 4.
Sous quel angle θ’ l’image de la Lune
donnée par la lunette est-elle vue ? |
|
Lunette de laboratoire :
-
Exploitation du schéma :
-
L’objet
B se situe à l’infini et
la Lunette astronomique est afocale :
-
En
conséquence, F’1,
F2 et le point
image A1 sont
confondus.
-
Les
distances :
-
Distance
focale de l’objectif : O1F’1 =
f1
≈ 50 cm
-
Distance
focale de l’oculaire : O2F2 =
f2
≈ 12,5 cm
-
Taille de
l’image intermédiaire A1B1 :
-
A1B1 ≈
4,65 mm
-
A1B1 ≈
4,7 mm
-
On est en
présence d’une image réelle renversée.
-
On trace
les points suivants :
-
F1 :
Le foyer objet de la lentille
L1
-
F1
est le symétrique de F’1
par rapport au centre optique
O1.
-
F’2
: Le foyer image de la lentille
L2
-
F’2
est le symétrique de F2
par rapport au centre optique
O2.
1.
Reproduction la
figure et tracé du trajet de deux rayons issus du point objet B.
-
Schéma :
- On trace le rayon provenant du point B situé à l’infini qui passe par le centre optique O1 de la lentille L1 et le point image
B1 et qui
n’est pas dévié. - On trace le rayon provenant du point B situé à l’infini qui passe par le foyer objet F1 de la lentille L1, parallèle au rayon précédent,
et qui émerge de la lentille parallèlement à l’axe optique
Δ.
-
Les deux
rayons convergent au point image
B1.
-
Le
rayon
rouge est parallèle à
l’axe optique, il émerge de la lentille
L2 en passant par son foyer image
F’2. - Comme le point B1 est situé dans le plan focal objet de la lentille L2, le
rayon vert émerge de cette
lentille parallèlement au
rayon rouge.
2.
Angle θ
sous lequel on voit la Lune à l’œil nu et sa valeur :
-
Schéma :
-
Considérons le triangle O1A1B1
rectangle en A1 :
-
3.
Distance
Terre-Lune :
-
Diamètre
de la Lune : D = 3,47 × 103 km
-
Schéma :
-
-
Application numérique :
-
-
La
distance dTerre-Lune
entre la Terre et la Lune varie au cours du temps :
-
3,56 × 105
km ≤ dTerre-Lune ≤ 4,06 × 105 km
-
La valeur trouvée appartient à l’intervalle.
4.
Angle θ’
sous lequel l’image de la Lune est vue à travers la lunette :
-
Pour faire
apparaître l‘angle θ’, il
faut tracer le
rayon issu de
B1 et passant par le centre optique O2
de l’oculaire.
-
Ce rayon
n’est pas dévié (rayon fuchsia).
-
-
On peut
calculer le grossissement de cette lunette laboratoire :
-
Comment
les angles θ et θ’ sont petits, on
peut faire l’approximation des petits angles :
-
-
Autre
relation :
-
Grossissement d’une lentille afocale :
-
|
||||||||||||||||||||||||||
8)- Exercice 20 page 400 : L’étoile Albireo :
|
L’étoile Albireo : L’étoile d’Albireo de la constellation du Cygne est une étoile
double. Ces deux étoiles sont vues à l’œil nu, depuis la Terre sous un
angle de 34 secondes d’arc.
A.
Fiche technique d’une lunette astronomique
afocale.
B.
Le pouvoir séparateur de l’œil. Le pouvoir séparateur de l’œil est l’angle minimal ε sous
lequel deux points lumineux peuvent être vus séparés. Pour un œil humain normal, ε =3,0 × 10–4 rad. Ainsi, deux points lumineux distincts, vus sous un angle inférieur à 3,0 × 10–4 rad, sont perçus comme un seul point lumineux. 1.
Exprimer, en radian, l’angle θ sous
lequel l’étoile double Albireo est vue à l’œil nu. 2.
: a.
Établir l’expression du grossissement d’une
lunette afocale. On pourra s’aider d’un schéma. b.
Calculer le grossissement maximal de cette
lunette astronomique. 3.
Calculer l’angle maximal θ’ sous
lequel est vue l’image de l’étoile double Albireo à travers cette
lunette afocale. 4.
Peut-on distinguer les deux étoiles
d’Albireo ?
-
Donnée : 1 degré d’arc est égal à
3600 secondes d’arc. |
L’étoile Albireo : 1.
Expression, en radian, l’angle θ sous
lequel l’étoile double Albireo est vue à l’œil nu.
-
Ces deux étoiles sont vues à l’œil
nu, depuis la Terre sous un angle de 34 secondes d’arc :
-
Tableau 01 : Degré
d’arc
Seconde d’arc
1 °
3600
‘’
θ
(°)
34 ‘’
-
-
Tableau 02 Degré
d’arc
radian
180
π
θ
(°)
θ
(rad)
-
2.
: a.
Expression du grossissement d’une lunette
afocale.
-
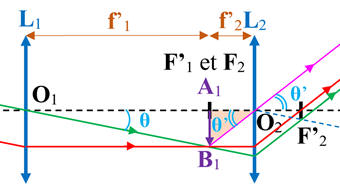
Schéma :
-
Le grossissement d’une lunette est le
rapport entre :
-
L’angle
θ sous lequel l’objet est
vu à l’œil nu et
-
L’angle
θ’ son image est vue à
travers la lunette.
-
Ainsi l’objet éloigné (B ∞) est vu sous l’angle
θ
et l’image A’B’ est vue sous l’angle θ’.
-
Le grossissement
G d’une lunette est donné par la relation suivante :
G
Grossissement : nombre sans unité
θ’
L’angle θ’
sous lequel son image est vue à travers la lunette
θ
L’angle θ sous lequel l’objet est vu à l’œil nu
Il
faut exprimer θ’ et θ dans la même unité
d’angle (° ou rad)
-
Considérons le triangle
O1A1B1
rectangle en A1 :
-
-
Comme
θ est petit en radian, on
peut faire l’approximation des petits angles :
-
-
Considérons le triangle
O2A1B1
rectangle en A1 :
-
-
Comme
θ’ est petit en radian,
on peut faire l’approximation des petits angles :
-
-
Grossissement de la lunette afocale :
-
b.
Grossissement maximal de cette lunette
astronomique.
-
La lunette astronomique afocale
possède deux oculaires :
-
f’2 = 10 mm ou
f’2 = 25 mm
-
Comme dans l’expression du
grossissement G, la
grandeur intervient f’2
au dénominateur, il faut prendre la plus petite des deux valeurs
pour avoir le grossissement maximal :
- 3.
Angle maximal θ’ sous lequel est vue
l’image de l’étoile double Albireo à travers cette lunette afocale.
-
-
Application numérique :
-
4.
Observation des deux étoiles d’Albireo :
-
Le pouvoir séparateur de l’œil est
l’angle minimal ε sous lequel deux points lumineux peuvent
être vus séparés.
-
Pour un œil humain normal, ε
=3,0 × 10–4 rad.
-
Or θ’ ≈1,2 × 10–2
rad > ε
-
L’étoile double est observée comme
deux points distincts à travers la lunette astronomique afocale avec
l’oculaire f’2
= 10 mm.
-
Observation avec
Stellarium :
►
Pouvoir séparateur de l’œil :
-
Définition : on appelle pouvoir
séparateur de l’œil, l ‘angle limite sous lequel 2 points lumineux
peuvent être séparés.
-
Le pouvoir séparateur d’un œil normal
est de l’ordre d’une minute d’angle soit 3,0 × 10–4 rad.
-
Remarque : la rétine a une structure
granulaire.
-
Elle est formée de cônes et de
bâtonnets.
-
Pour que la rétine puisse séparer les
images de deux points lumineux, il faut que la lumière des deux
images excite des cellules séparées par au moins une cellule non
excitée (diamètre d’une cellule : ϕ = 2,5 μm.
![]()
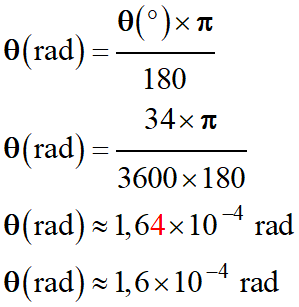
![]()
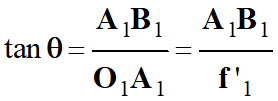
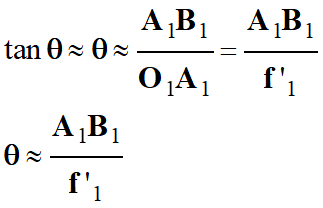
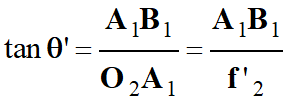

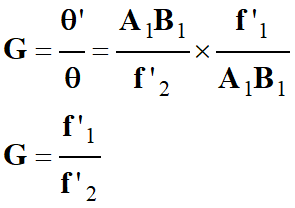

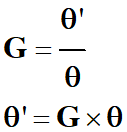
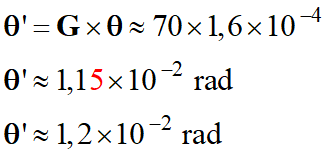

![]()
|
|