|
Mouvement dans un champ de gravitation |
|
|
|
|
|
|
QCM N°
13
Mouvement dans
un champ de gravitation
Mouvement des
satellites et des planètes
Lois de Kepler
Pour chaque
question, indiquer la (ou les) bonne(s) réponse(s). |
|||||
|
|
|||||
|
|
Énoncé |
A |
B |
C |
R |
|
1 |
Pour étudier
le mouvement
de la Lune
autour de la Terre,
le référentiel
le plus approprié
est : |
Le référentiel
géocentrique |
Le référentiel
terrestre |
Le référentiel
héliocentrique |
A |
|
2 |
La force de
gravitation exercée
par la Terre
sur la Lune
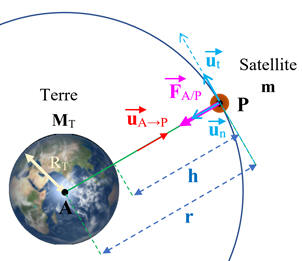
(Schéma A) a
pour expression : |
|
|
|
C |
|
3 |
D’après la
deuxième loi de Newton,
le vecteur
accélération de la Lune,
lors de son
mouvement autour de la
Terre (schéma
A), a pour
expression : |
|
|
|
A |
|
4 |
Le vecteur
vitesse de la Lune lors
de son
mouvement circulaire
autour de la
Terre est : |
Tangent au
mouvement |
Normal au
mouvement |
De valeur
constante |
AC |
|
5 |
Lorsqu’une
comète sur son orbite,
dans le
référentiel héliocentrique,
s’éloigne du
Soleil, la valeur de la
vitesse :
|
augmente |
diminue |
Reste
constante |
B |
|
6 |
D’après la
troisième loi de Kepler
appliquée dans
le référentiel
héliocentrique, pour une trajectoire
circulaire de
rayon r et de période
de révolution
T : |
|
|
|
AB |
|
7 |
D’après la
troisième loi de Kepler
appliquée au
référentiel
héliocentrique, pour une trajectoire
circulaire de
rayon
rplanète
et de période de révolution
Tplanète :
|
|
|
|
AB |
|
8 |
Dans le
référentiel héliocentrique,
et dans
l’approximation des
trajectoires
circulaires,
le rapport
3,0 × 10–19
s2 . m–3. La période de
révolution de
Vénus est : - (1an = 3,156 × 107 s et 1 jour = 86400 s)
|
3,8 × 1014
s |
2,3 × 103
jours |
1,9 × 107
s |
C |
QCM
réalisé avec le logiciel Questy
Pour s’auto-évaluer
La force de gravitation :




Mouvement des satellites et des planètes :

Ou
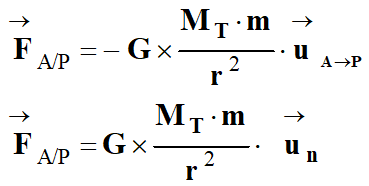
Caractéristiques du vecteur accélération
![]() du satellite :
du satellite :
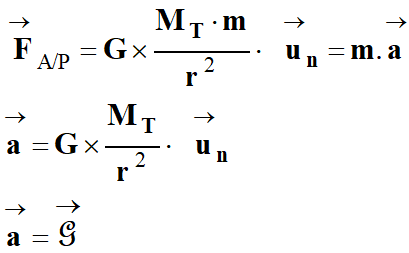
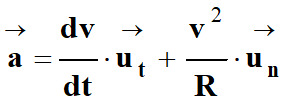
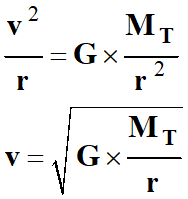
Expression du vecteur vitesse ![]() du satellite :
du satellite :
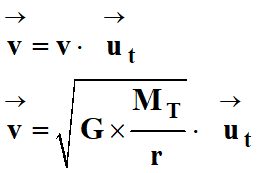
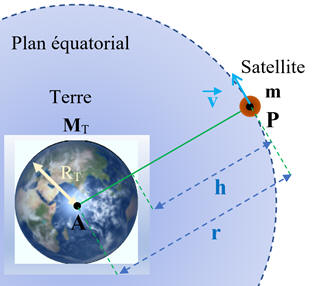
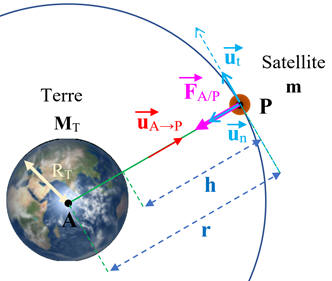
Les lois de Kepler :
Première loi de Kepler : Loi des orbites.
Définition d’une ellipse :
Deuxième loi de Kepler : Loi des aires.
Troisième loi de Kepler : Loi des périodes.
 .
.Période de révolution d’une planète du système solaire
:
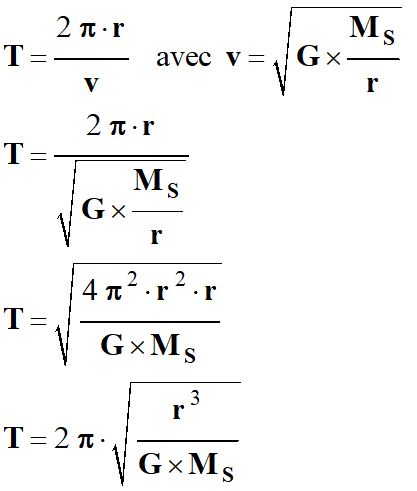
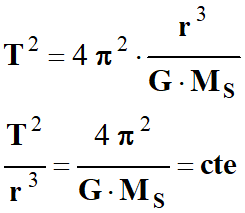

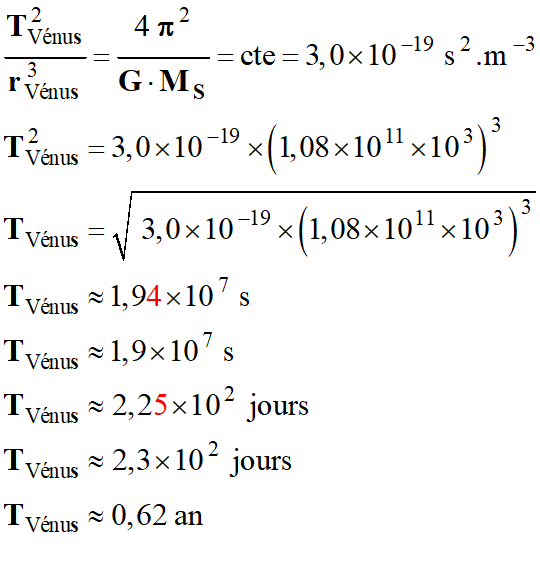
|
|