|
Mouvement et Forces |
|
|
|
|
|
|
QCM N° 11
Mouvement et
forces
Pour chaque
question, indiquer la (ou les) bonne(s) réponse(s). |
|||||
|
|
Énoncé |
A |
B |
C |
R |
|
1 |
Pour décrire le
mouvement de la
Lune autour de la
Terre, le
référentiel
le plus approprié
est
le référentiel :
|
Terrestre |
Géocentrique |
Héliocentrique |
B |
|
2 |
Le mouvement
décrit
sur cette
chronophotographie
ci-dessous est :
|
Uniforme |
Décéléré |
Accéléré |
C |
|
3 |
Dans quelles
situations
la somme
vectorielle des
forces est-elle
nulle ? |
Un bus
roulant en
ligne droite
et à vitesse
constante |
Un bus
freinant en
ligne droite
jusqu’à
l’arrêt. |
Un enfant
dans un
manège
qui tourne |
A |
|
4 |
On considère un
parachutiste en
chute
verticale. Le
système
{parachute+parachutiste}
de masse m
= 80 kg a un
mouvement
rectiligne
uniforme. La
force de
frottement
exercée
sur le système
vaut :
Donnée :
norme du champ
de pesanteur
terrestre :
g
= 9,81 N . kg–1 |
On ne
peut pas
savoir |
8,2 N |
7,8 × 102
N |
C |
|
5 |
La relation liant
la
variation
vitesse d’un
système
de masse m
entre
t
– Δt et t + Δt et la
somme
appliquées est : |
|
|
|
BC |
|
6 |
Une voiture de
masse
m
= 2,1 t passe, sur une
route
horizontale, de 0
à 27 m . s–1
en 2,4 s.
Dans cette phase
d’accélération,
tout se passe comme si la
voiture n’était
soumise
qu’à une force de
propulsion
constante. La norme de
cette force vaut : |
5,4 × 10–3
N |
2,4 × 101
N |
2,4 × 104
N |
C |
|
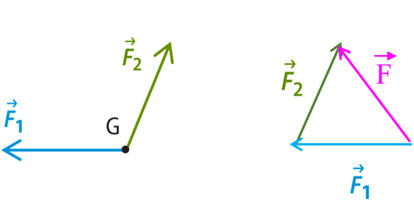
7 |
On considère un
point
G soumis à trois
forces
représentées
ci-dessous.
Dans quels cas le
mouvement du
point G
peut-il être
rectiligne uniforme. |
|
|
|
C |
|
8 |
Soient trois
forces
appliquées à un
système.
Leur somme
construit ainsi :
|
|
|
|
AB |
|
9 |
On considère un
point
dont on donne les
équations
horaires de la
vitesse (vx
et vy sont en
mètres par
seconde et t
est en
secondes) :
Les équations
horaires
de la position
peuvent être :
|
|
|
|
A |
|
10 |
On considère un
point
dont on donne les
équations
horaires de la
vitesse (vx
et vy sont en
mètres par
seconde et t
est en
secondes) :
Les équations
horaires
de son
accélération
sont : |
|
|
|
B |
|
11 |
On donne
l’évolution de
l’accélération
d’un
système suivant
un
mouvement
rectiligne
le long de l’axe
(Ox)
Quelle courbe
décrit
le mieux le
système ? |
|
|
|
B |
|
12 |
On donne
l’évolution de
l’accélération
d’un
système suivant
un
mouvement
rectiligne
le long de l’axe
(Ox)
Quelle courbe
décrit
le mieux la
vitesse de
ce système ? |
|
|
|
A |
|
13 |
On donne
l’évolution
de la vitesse
d’un
système en
mouvement
rectiligne de
long
d’un axe (Ox).
Quelle est la
courbe
de l’accélération
associée ? |
|
|
|
C |
QCM réalisé avec le logiciel Questy
Pour s’auto-évaluer
Le référentiel géocentrique.
-
L’origine du repère lié au référentiel
Géocentrique est située au centre de la Terre.
-
L’axe z’Oz
est orienté vers une étoile lointaine : on peut choisir l’étoile polaire.
-
Les axes
x’Ox et y’Oy
sont situés dans le plan équatorial et ils sont orientés vers des étoiles
lointaines supposées fixes.
-
Ce référentiel est commode pour l’étude des
satellites de la Terre comme la Lune.
-
Ce référentiel n’est pas entraîné dans le
mouvement de rotation de la Terre.
-
Dans ce référentiel, la Terre est animée d’un
mouvement de rotation uniforme de l’ouest vers l’est, autour de l’axe des pôles.
-
Ce référentiel est bien utile pour étudier le
mouvement des satellites de la Terre.
Chronophotographie d’un mouvement :
-
Le point mobile
M parcourt des
distances de plus en plus grandes pendant des durées égales.
-
Le mouvement du point
M est accéléré.
Les différents types de mouvement rectiligne :
-
Un point est animé d’un mouvement rectiligne
si sa trajectoire est une droite.
-
Mouvement rectiligne uniforme :
-
Le point mobile
M parcourt des
distances égales pendant des durées égales
-
Mouvement rectiligne varié : (il peut être
accéléré ou retardé)
-
Mouvement accéléré :
-
Le point mobile
M parcourt des
distances de plus en plus grandes pendant des durées égales.
-
Mouvement décéléré ou retardé :
-
Le point mobile
M parcourt des
distances de plus en plus petites pendant des durées égales
Mouvement uniforme :
-
Dans un référentiel donné, un
système est animé d’un mouvement uniforme si la valeur de sa vitesse
v est constante au cours du mouvement.
-
Le mobile parcourt des distances égales
pendant des durées égales :
-
Chronophotographie d’un mouvement rectiligne
uniforme :
-
Mouvement circulaire uniforme :
Somme vectorielle des forces appliquées à un système :
-
Le bus est animé d’un mouvement rectiligne
uniforme.
-
le vecteur vitesse
![]() ne
varie pas :
ne
varie pas :
![]() .
.
-
Il est soumis à des forces dont les effets se
compensent :
![]()
-
Si le bus, freine, sa vitesse diminue pour
s’annuler lorsqu’il est à l’arrêt :
-
![]()
-
Lors d’un mouvement
de rotation, le vecteur vitesse du système change de direction :
-
![]()
-
Le vecteur vitesse
peut changer de valeur ou (et) de direction au cours du mouvement d’un système.
-
Énoncé : Principe
d’Inertie :
|
Lorsque les forces qui s’exercent sur
un système se compensent alors le vecteur vitesse
|
-
Autre formulation :
|
Lorsque les forces qui s’exercent sur
un système se compensent, alors le système reste immobile, ou
reste en mouvement rectiligne uniforme. C’est-à-dire :
|
-
Réciproque du principe d’Inertie :
|
Si le vecteur vitesse
alors le système est soumis à de
forces qui se compensent.
|
Chute verticale :
-
Le système est animé
d’un mouvement rectiligne uniforme par rapport à la Terre :
-
D’après la réciproque
du principe d’inertie :
-
![]()
-
Dans le référentiel
terrestre, le système est soumis à son poids
![]() et
à la force de frottement
et
à la force de frottement
![]() .
.
-
Photo :

-
Schéma de la
situation :
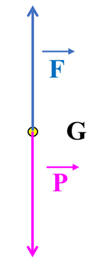
-
![]()
-
Les deux forces sont
égales et opposées :
-
P
= m .
g =
F = 9,81 × 80
-
F
≈ 7,8 × 102 N
Vecteur variation de vitesse :
-
Dans un
référentiel donné, si un système de masse
m
constante est soumis à une ou plusieurs forces constantes, le vecteur variation
de vitesse
![]() de
ce système pendant une durée très courte
Δt
et la somme de ces forces
de
ce système pendant une durée très courte
Δt
et la somme de ces forces
![]() sont reliés par la relation :
sont reliés par la relation :
|
|
Valeur de
la force F en newton (N) |
|
Valeur de
la masse m en kilogramme (kg) |
|
|
Valeur de
la durée Δt en seconde (s) |
-
Ces deux vecteurs sont
colinéaires.
-
La somme vectorielle
des forces qui s’exercent sur un système
![]() est
également appelée résultante des forces notée :
est
également appelée résultante des forces notée :![]()
-
![]()
-
Plus la masse d’un
système est grande et plus il est difficile de modifier le mouvement de ce
système.
-
Si
Δt
→ 0, et la relation devient :
-
![]()
Force de propulsion :
|
|
Valeur de
la force F en newton (N) |
|
Valeur de
la masse m en kilogramme (kg) |
|
|
Valeur de
la durée Δt en seconde (s) |
-
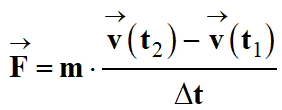
-
On considère que le
mouvement est rectiligne : tous les vecteurs ont la même direction et le même
sens.
-
La relation peut
s’écrire :
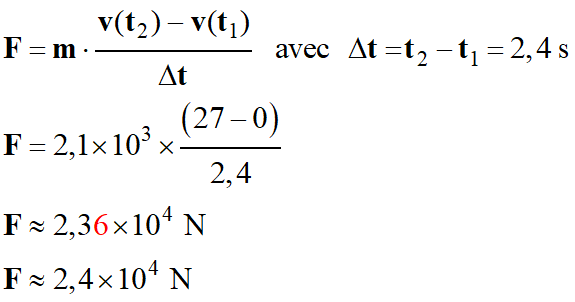
Mouvement rectiligne uniforme :
-
D’après la réciproque
du principe d’inertie :
|
Si le vecteur vitesse
alors le système est soumis à de
forces qui se compensent.
|
-
![]()
-
Cas
A :
![]() :
:
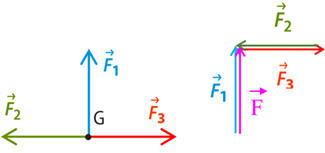
-
Cas
B : ![]()
-
Cas
C : ![]()
-
Le système est soumis
à des forces dont les effets se compensent.
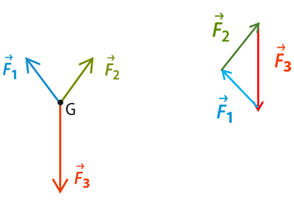
-
Le mouvement du point
G peut être
rectiligne uniforme (le point G
peut être immobile)
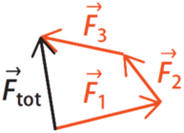
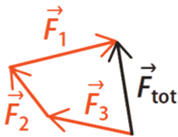
Somme vectorielle :
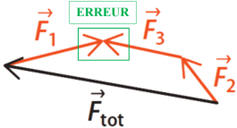
-
Le résultat d’une
somme vectorielle ne dépend pas de l’ordre des vecteurs.
-
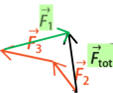
Dans le cas
C, lors de la
construction, l’origine de la force
![]() n’est
pas bonne.
n’est
pas bonne.
-
Erreur :
-
Il faut continuer à
partir de l’extrémité du vecteur force
![]() .
.
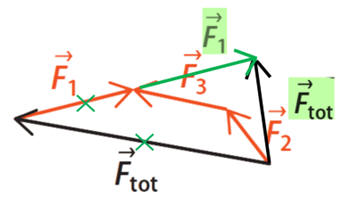
-
On retrouve le même
vecteur :![]()
| A | B | C |
 |
 |
 |
Équations horaires :
Chap N° 05 Cinématique et dynamique newtonienne. (TS
1010)
Chap N° 11 Mouvement et forces (terminale 2020)
|
Vecteur
position |
Vecteur
vitesse |
Vecteur
accélération |
|
|
|
|
-
Dans
le cas présent, on connait les coordonnées du vecteur vitesse en fonction du
temps.
-
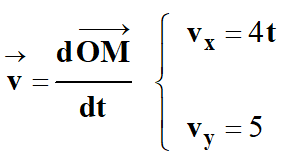
-
La détermination du
vecteur position nécessite de rechercher la primitive par rapport au temps de
chaque coordonnée du vecteur accélération en tenant compte des conditions
initiales.
-
On cherche les
primitives des équations précédentes.
-
Il apparaît des
constantes qui sont liées aux conditions initiales.
-
Les constantes
d’intégration apparues dans les primitives sont liées aux conditions initiales.
-
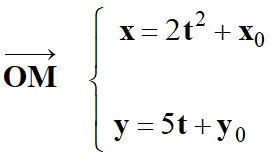
-
Dans le cas présent, au temps
t = 0 s,
x0
= 4 et y0
= 0
-
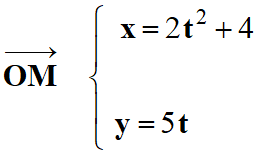
Équation horaire et coordonnées du vecteur
accélération :
|
Vecteur
accélération |
|
|
-
Le vecteur
accélération est égal à la dérivée du vecteur vitesse par rapport au temps :
-
Comme : 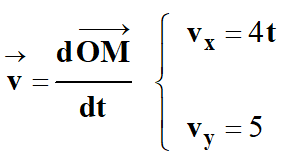
-
Alors : 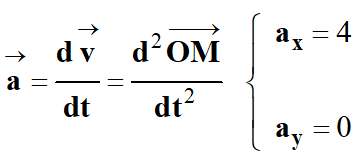
Exploitation de la courbe représentant l’évolution de
l’accélération :
-
Évolution de la
position du système :
-
D’après le graphe :
ax
= f (t)
-
L’accélération est
constante et négative :
-
ax
= cte < 0
-
vx
est une primitive de ax.
-
vx
= ax
. t +
v0x
-
l’abscisse
x est une primitive
de vx
-
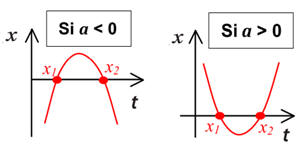
x
= ½ ax
. t2
+ v0x
. t +
x0
-
Ne pas oublier que la
grandeur ax
< 0
-
En conséquence la
bonne réponse est la réponse B :
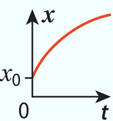
Exploitation de la courbe représentant l’évolution de
l’accélération :
-
Évolution de la
vitesse du système :
-
D’après le graphe :
ax
= f (t)
-
L’accélération est
constante et négative :
-
ax
= cte < 0
-
vx
est une primitive de ax.
-
vx
= ax
. t +
v0x
-
le coefficient
directeur de la droite est négatif.
-
En conséquence la
bonne réponse est la réponse A :
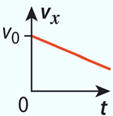
Exploitation
de la courbe représentant l’évolution de la vitesse :
-
Mouvement rectiligne
uniforme suivant l’axe (Ox).
-
D’après le graphe :
vx
= f (t)
-
La valeur de la
vitesse est constante : vx
= v0
= cte > 0
-
![]()
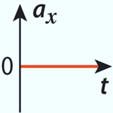
-
La bonne réponse est
la réponse C :
|
|