I- Le Principe d’Inertie.

1)- Introduction :

-     Le système étudié est ramené à un seul point.

-     L’ensemble des forces appliquées au système est représenté en ce point.

2)- Effet d’une force sur le mouvement d’un système.

-     Exemple 1 : Effet du poids sur une balle qu’on lance.

-     Exemple 2 : Phénomène d’électrisation :

-     Effet d’une force électrostatique sur des petits morceaux de papiers.

-     Une force s’exerçant sur un système peut modifier :

-     La valeur de la vitesse,

-     Et/ou la direction du mouvement de ce système.

-     Elle peut donc modifier le vecteur vitesse du système.

-     Additif : une force peut aussi déformer un système (exemple : déformation d’un ressort sous l’effet d’une force).

3)- Principe d’Inertie.

-     Deux forces se compensent si elles ont

-     La même droite d’action

-     Des sens opposés,

-     Et la même valeur.

-     La somme vectorielle des représentants de ces forces est égale au vecteur nul :

-      

-     Énoncé : Principe d’Inertie :

-     Autre formulation :

-     Réciproque du principe d’Inertie :

Situation 1 :

-     On pose une pierre de curling, de masse m = 19,96 kg, sur la patinoire plane et horizontale. 

-     On néglige les forces de frottements et l’action de l’air sur la pierre de curling

-     On prend : g = 10 N / kg).

-     Quelles sont les actions mécaniques qu’elle subit ?

-     Le système est la pierre de curling.

-     Le système extérieur est tout ce qui ne fait pas partie de la pierre de curling.

-     La pierre de curling est en interaction avec la Terre.

-     C’est le poids de la pierre de curling :

-     La pierre de curling est en interaction avec la glace.

-     La glace empêche la pierre de curling de s’enfoncer :

-     La pierre de curling est immobile

-     D’après la réciproque du principe d’Inertie le système est soumis à des actions qui se compensent.

-     Dans ce cas, on dit que, son poids  et la force exercée par la glace sur la pierre  sont deux forces qui annulent leurs effets : elles se compensent.

-     Forces qui se compensent :

-     Deux forces qui se compensent ont même direction, même valeur, mais des sens opposés.

-     Elles sont représentées par deux vecteurs opposés.

-     Leur somme vectorielle est égale au vecteur nul.

-      

-     Schéma :

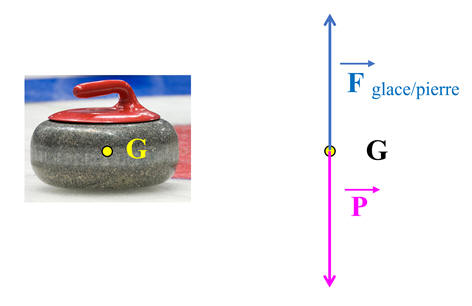
-     L’application de la réciproque du principe d’inertie à la situation de la pierre de curling permet de déterminer les caractéristiques de la force .

-     La réciproque du principe d’inertie permet d’affirmer que la pierre de curling est soumise à des actions mécaniques dont les effets se compensent :

-      

-     En conséquence : P = F_glace/pierre ≈ 200 N

-     Caractéristiques de la force :

Situation 2 :

-     On lance cette même pierre sur la patinoire.

-     Quelles sont les actions mécaniques qu’elle subit ?

-     Le système est la pierre de curling.

-     Les forces de frottement sont négligeables.

-     La pierre de curling est soumise aux mêmes actions mécaniques  et .

-     Lorsque la pierre de curling se déplace sur la patinoire,

-     Elle est animée d’un mouvement rectiligne uniforme par rapport à la patinoire (Référentiel terrestre).

-     D’après la réciproque du principe d’inertie :

-     La réciproque du principe d’inertie permet d’affirmer que la pierre de curling est soumise à des actions mécaniques dont les effets se compensent :

-      

-     En conséquence : P = F_glace/pierre ≈ 200 N

4)- Contraposée du principe d’inertie :

-     Énoncé 1 :

-     Énoncé 2 :

-     Réciproque de la contraposée du principe d’Inertie :

-     Exemple : à finir

II- La chute libre verticale.

1)- Systèmes en chute libre verticale.

a)-   Définition :

-     Un système est en chute libre lorsqu’il n'est soumis qu’à l’action de son poids .

 Expérience.

-     On prend une feuille de papier que l'on plie.

-     Lorsque la surface de la feuille devient petite, on s'aperçoit que celle-ci tombe suivant une ligne verticale.

-     On peut considérer que les objets de petites tailles se déplaçant sur une faible distance sont en chute libre.

-     Dans l’air, on peut considérer que la chute est libre :

-     Pour un petit objet lourd de petites tailles

-     Se déplaçant sur une faible distance.

-     Ainsi, on peut négliger la résistance de l’air lors de cette étude.

-     En toute rigueur, l’étude de la chute libre doit se faire dans le vide : tube de Newton.

-     Remarque : une chute libre est dite à une dimension car le mouvement s’effectue suivant la verticale du lieu : c’est-à-dire suivant une seule direction.

-     La chute libre peut être effectuée sans vitesse initiale ou avec une vitesse initiale faisant un angle α avec la verticale.

b)-  Chute libre sans vitesse initiale :

-     Le fichier : CHGOLF.AVI.

-     Propriétés du clip :

-   Chute libre d'une balle de golf. 

-     Étude chronophotographique :

Cliquer sur l'image pour l'agrandir

-     Représentation à l’instant t :

-     Le système est soumis à l’action du poids

-     D’après la réciproque de la contraposée de principe d’Inertie :

-     On remarque que le système parcourt des distances de plus en plus grandes pendant des intervalles de temps égaux.

-     En conséquence, la valeur de la vitesse varie au cours du temps, donc le vecteur vitesse du système varie au cours du temps.

-     Remarque :

-     Le vecteur vitesse du système garde la même direction et le même sens au cours du mouvement.

Cliquer sur l'image pour l'agrandir

c)-   Chute libre avec vitesse initiale :

Vidéo

-     Propriétés du clip :

-     Étude chronophotographique :

Cliquer sur l'image pour l'agrandir 

-     Étude avec AVIMECA 2.7

-     Le système est soumis à son poids :

-     D’après la réciproque de la contraposée de principe d’Inertie :

-     Sur l’enregistrement, on remarque que le vecteur vitesse change de direction et de valeur à chaque instant.

-     Lorsque la balle monte, la valeur de la vitesse diminue et lorsque la balle descend la valeur de la vitesse augmente.

d)-  Autres cas :

-     Chute dans l’huile :

-     Chute verticale dans un fluide :

-     Vidéo : Bille50.zip

2)- Variation du vecteur vitesse d’un système en chute libre verticale :

-     Le vecteur vitesse d’un système en chute libre verticale varie entre deux instants voisins.

-     Le mouvement d’un système en chute libre n’est pas rectiligne uniforme.

III- Applications.

1)- Quelques mouvements caractéristiques :

-     Étude chronophotographique

-     Le mouvement rectiligne uniforme :

-     Le mouvement rectiligne accéléré :

-     Le mouvement rectiligne retardé ou décéléré :

-      Mouvement curviligne varié (accéléré puis décéléré)

-     Mouvement circulaire uniforme :

-     Expérience :

-     Le mobile autoporteur, maintenu par un fil tendu inextensible, est lancé sur la table à digitaliser.

-     La table est horizontale.

-     On enregistre la position d’un point particulier du système à intervalles de temps égaux τ après avoir lâché le mobile.

Vidéo

2)- QCM :

3)- Exercices :