|
Modéliser une action mécanique Cours |
|
|
|
|
|
|
II- Le principe des actions réciproques. Troisième loi de Newton. |
|
1)- Forces
d’interaction gravitationnelle. |
|
1)-
Poids d’un corps sur la Terre et sur la Lune. |
|
1)-
Exercice 5 page 178 : Schématiser une force. 2)-
Exercice 6 page 178 : Classer des actions. 3)-
Exercice 9 page 178 : Caractériser l’interaction
gravitationnelle. 4)-
Exercice 11 page 179 : Calculer une force gravitationnelle. 5)-
Exercice 14 page 179 : Exploiter une relation vectorielle. 6)-
Exercice 16 page 179 : Calculer un poids sur la Lune : 7)-
Exercice 21 page 180 : Hubble et la Terre. 8)-
Exercice 22 page 180 : Côté maths. 9)-
Exercice 23 page 180 : Interaction gravitationnelle et poids. 10)-
Exercice 26 page 181 : J’ai pesé la Terre.
|
|
Modélisation d'une action mécanique Principe de l'interaction Exemples de forces |
I-
Modélisation d’une action mécanique par une force.
- Le système étudié est modélisé par un point.
- Tout ce qui ne constitue pas le système est appelé
milieu
extérieur, système extérieur ou
extérieur.
- Le système étudié peut être soumis à différentes
actions
mécaniques de la part de l’extérieur.
a)- Exemple : Ballon immobile percuté par le pied d’un footballeur.
- Cas d’un ballon, de masse
m = 450 g, posé sur le sol
et percuté par le pied du footballeur
- On prendra :
g = 10 N / kg

![]() Question : Quelles sont les actions mécaniques que subit le ballon
à l’instant de l’impact ?
Question : Quelles sont les actions mécaniques que subit le ballon
à l’instant de l’impact ?
-
Le système étudié est le
ballon.
-
Tout ce qui ne constitue pas le système est appelé milieu
extérieur au système extérieur ou extérieur.
-
Le ballon est immobile sur le sol et il est frappé par le pied du
footballeur.
-
Ici, on négligera l’action de l’air sur le ballon.
-
Faire le bilan des actions mécaniques exercées par le milieu
extérieur sur le ballon :
-
Le ballon est en
interaction avec
la Terre.
-
La Terre attire le ballon, c’est une action à distance répartie
sur le volume du ballon.
-
Le ballon est en
interaction avec
le sol.
-
Le sol empêche le ballon de s’enfoncer dans le sol. Il empêche le
ballon de tomber.
-
C’est une action de contact qui est répartie sur la surface de
contact entre le ballon et le sol.
-
Le ballon est en
interaction avec
le pied
(la chaussure) du
footballeur.
-
Le pied pousse le ballon.
-
C’est une action de contact qui est répartie sur la surface de
contact entre le ballon et le pied.
![]() Remarque :
Remarque :
-
Les actions mécaniques à prendre en compte sont toutes des actions
exercées par le milieu extérieur sur le système étudié.
-
Lorsque le système est en mouvement rapide, il faut tenir de
l’action de l’air sur le système.
b)- Action mécanique.
-
Une action mécanique exercée par l’extérieur sur le système étudié
est modélisée par une force.
-
Cette force est représentée par un segment fléché, appelé vecteur
force noté : ![]()
![]() Caractéristiques :
Caractéristiques :
-
L’origine : point d’application de la force, point où l’on
considère que la force s’exerce.
-
La
direction : Celle de la droite d’action de la force
-
Le
sens : celui de la force.
-
La
valeur de la force.
![]() Remarque
1 :
Remarque
1 :
-
La longueur du représentant est proportionnelle à la valeur de la
force.
-
La valeur d’une force se mesure à l’aide d’un dynamomètre.
-
L’unité de force est le newton (N).
![]() Remarque 2
:
Remarque 2
:
-
Sur un schéma, une force est représentée par un segment fléché,
appelé vecteur.
-
Pour simplifier, on représente le système étudié par un point (le
plus souvent, on prend le centre d’inertie G du système ou un point
particulier).
-
Les forces exercées par le milieu extérieur sur le système sont
alors représentées à partir de ce point.
-
Lorsque la valeur de la force est connue, la longueur du segment
fléché est proportionnelle à cette valeur.
-
Pour ce faire, on utilise une échelle : exemple : 1 cm ↔ 1 N.
c)-
Schéma de la situation : Ballon immobile percuté par le pied d’un
footballeur
-
Poids du ballon :
P =
m . g ≈ 4,5 N.
-
Lorsque la valeur de la force n’est pas connue (ici c’est le cas
de l’action du pied sur le ballon), on donne une longueur approximative.
d)- Action de contact et action à distance.
![]() Une action
qui ne s’exerce que lorsqu’il y a contact entre le système étudié et l’extérieur
est appelé action de contact.
Une action
qui ne s’exerce que lorsqu’il y a contact entre le système étudié et l’extérieur
est appelé action de contact.
-
Exemple :
-
L’action exercée par le sol sur le ballon
![]() est une action de
contact.
est une action de
contact.
-
De même l’action exercée par le pied sur le ballon
![]() est une action de
contact.
est une action de
contact.
![]() Une action
qui s’exerce sans contact entre le système étudié et l’extérieur est appelé
action à distance.
Une action
qui s’exerce sans contact entre le système étudié et l’extérieur est appelé
action à distance.
-
Exemple : L’action exercée par la Terre sur le ballon
![]() est une action à
distance.
est une action à
distance.
![]() Remarque 3 :
Remarque 3 :
-
Un diagramme objets-interactions permet de faire l’inventaire des
interactions à distance (représentées par des pointillés) et de contact
(représentées par des traits pleins) dans lequel le système est engagé.
-
Chaque action exercée sur le système est modélisée par une force.
-
Diagramme de la situation : Ballon immobile percuté par le pied
d’un footballeur.
II-
Le
principe des actions réciproques. Troisième loi de Newton.
-
Énoncé :
-
Soient deux systèmes
A et
B.
-
A
est situé au point
O
de l’espace et B
est situé au point P
de l’espace.
-
Lorsqu’un système
A exerce sur un
système B une
action mécanique représentée par le vecteur force
![]() localisée en
P.
localisée en
P.
-
Le système
B
exerce sur un système
A
une action mécanique représentée par le vecteur force
![]() localisée en
O.
localisée en
O.
-
Les forces
![]() et
et
![]() ont même support
et :
ont même support
et :
-
![]() .
.
-
Schéma :
Ou
-
Remarque : cette propriété est toujours vraie, que les corps
soient au repos ou en mouvement.
1)- Forces d’interaction gravitationnelle.
-
Pour un observateur terrestre,
-
La trajectoire de
-
Le mouvement de
-
Le référentiel terrestre n’est pas adapté pour l’étude du
mouvement de
-
On préfère utiliser le référentiel Géocentrique. (voir
les référentiels)
-
Dans le référentiel Géocentrique, la trajectoire de la Lune est
pratiquement un cercle de rayon R = 384 000 km.
-
Soit 60 fois le rayon de la Terre.
-
La durée d’un tour que l’on appelle la période sidérale est de
27,3 jours.
-
Tournant autour de la Terre, on peut en déduire que la Lune est
soumise à une force exercée par la Terre.
-
La force exercée par la Terre sur la Lune est une force d’origine
gravitationnelle.
-
La Terre agit sur la Lune, mais la Lune agit aussi sur la Terre
(phénomène des marées)
-
De même, le Soleil exerce une action attractive sur toutes les
planètes du système solaire.
-
Chaque planète du système solaire est attirée par le Soleil et par
toutes les autres planètes.
-
On dit qu’elles sont en interaction.
- En 1987, Isaac NEWTON a écrit un texte que l’on peut traduire :
« l’action qui retient la Lune dans son orbite est dirigée vers la Terre.
Sa
valeur est inversement proportionnelle au carré de la distance entre le centre
de la Lune et le centre de la Terre ... »
-
C’est l’interaction gravitationnelle.
2)-
La Loi
d’attraction gravitationnelle :
-
Énoncé :
-
Deux corps ponctuels, de masses
mA
situé en A
et mB
situé en B, séparés par une distance
d,
exercent l’un sur l’autre des forces attractives, de même valeur :
|
|
G est appelé la constante de gravitation universelle
G
≈
6,67
x
10
– 11 m
3 . kg–
1 .
s–
2 |
|
FA/B
= FB/A :
Valeur de la
force en Newton N. |
|
|
mA
et mB :
Valeur des masses en kg. |
|
|
d
: Distance séparant les deux masses
ponctuelles : en m |
|
|
Relations vectorielles :
Et
|
|
-
Les forces se représentent par des flèches, appelées vecteurs, de
même longueur, de même direction, mais de sens opposés.
-
Caractéristiques du vecteur force ![]() :
:
|
|
Point
d’application : B |
|
Direction : la
droite (AB) |
|
|
Sens : de B
vers A |
|
|
Valeur de la
force :
|
-
Caractéristiques du vecteur force ![]() :
:
|
|
Point
d’application : A |
|
Direction : la
droite (AB) |
|
|
Sens : de A
vers B |
|
|
Valeur de la
force :
|
-
Le poids
PA d’un objet à la surface d’un astre
A est assimilé à la force d’interaction gravitationnelle exercée par cet
astre sur cet objet.
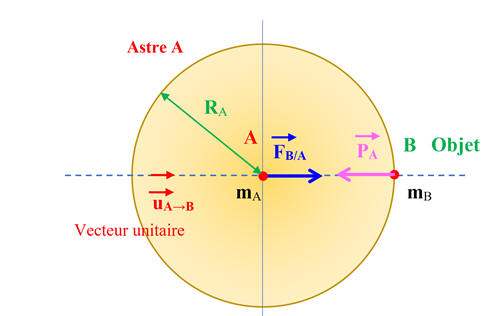
-
L’astre
A, de rayon RA, est assimilé à un
point matériel de masse mA situé en
A.
-
L’objet
B est assimilé à un point matériel de masse
mB
situé en B, à la surface de l’astre
A, à la distance
RA
(rayon de l’astre).
-
Expression du poids
PA de l’objet :
-
Expression vectorielle :
![]()
-
Expression de la valeur du poids de l’objet
B sur l’astre
A :
-
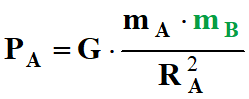
-
Tout corps
A, de centre C et de masse
m,
placé au voisinage de la Terre subit une
attraction.
-
Le centre de la Terre est noté
T, sa masse mT
et son rayon R
T.
-
Schéma :
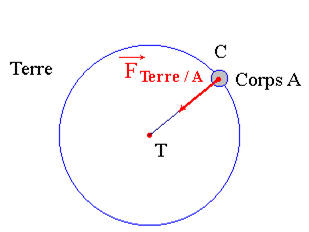
-
L’attraction exercé par la Terre sur le corps
A est
modélisée par la force ![]()
-
Caractéristiques de cette force :
|
|
Point
d’application : C |
|
Direction : la
droite (TC). Elle passe par le
centre de la Terre. C’est la verticale
du lieu |
|
|
Sens : de C
vers T. La force est
orientée vers le bas. |
|
|
Valeur de la
force :
Si le corps est au
voisinage de la Terre ou à la surface de
la Terre d
≈ R
T. Alors :
|
![]() Remarque :
Remarque :
-
Pour tous les objets qui se trouvent à la surface de la Terre ou
au voisinage de la Terre, le terme
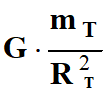 est
le même.
est
le même.
-
Il est caractéristique de la Terre.
-
On peut calculer sa valeur :
-
Données :
G ≈ 6,67
x 10
– 11
m 2
. kg–
2 . N
-
et R
T = 6,38
x 10
3
km
-
Masse de la Terre :
m
T
= 6,0
x 10
24
kg
-
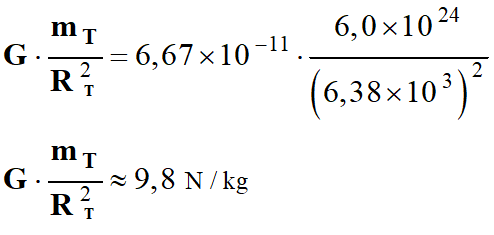
-
On retrouve la valeur de g ≈ 9,8 N / kg
-
On peut écrire la relation suivante, pour les objets de masse
m
au voisinage de la Terre :
-
F
Terre / A ≈ 9,8
m
-
On retrouve l’expression du poids d’un corps de masse
m au
voisinage de la Terre vue au collège.
-
P =
m .
g
|
|
Point
d’application : C : centre de gravité
du corps A |
|
Direction :
Verticale du lieu |
|
|
Sens : orientée
vers le bas. |
|
|
Valeur de la
force : P
= m . g Avec g = 9,8
N / kg, g
est l’intensité de la pesanteur. |
-
Sur la terre, tout corps de masse
m est soumis à une force
appelée poids du corps :
-
Expression du poids :
P =
m.g.
-
P poids en Newton N,
m la masse en kg et
g le
facteur d’attraction terrestre : g = 9,8 N / kg.
-
Le poids d’un objet sur Terre est pratiquement égal à la force
gravitationnelle exercée par
-
Remarque : la différence entre le poids d’un objet sur la Terre et
la force de gravitation exercée par
-
Le poids d’un corps peut s’identifier à la force gravitationnelle
exercée par la Terre sur l’objet.
-
La valeur du poids varie en fonction de la latitude et de
l’altitude.
![]() Conséquence :
Conséquence :
-
Le poids d’un corps situé au
voisinage de la Terre est assimilé à la force d’attraction gravitationnelle que
la Terre exerce sur ce corps.
-
L’action exercée par la Terre sur les
corps proches de la surface se nomme la pesanteur.
-
Exemple 1 : Système maintenu par un fil. L’ensemble est immobile.

-
Le système : Pomme.
-
La pomme est en interaction avec le fil, la tension du fil
![]() .
.
-
La pomme est en interaction avec la Terre : Poids de la pomme :
-
![]() avec
P = m .
g
avec
P = m .
g
-
Dans le cas présent, le dynamomètre mesure aussi bien la tension
![]() du fil que le poids
du fil que le poids
![]() de la pomme.
de la pomme.
-
Caractéristiques de la tension
![]() du fil :
du fil :
-
La pomme est soumise à l’action d’un fil.
-
La force modélisant cette action a :
-
Une direction : celle du fil.
-
Un sens : du système vers le fil.
![]() Remarque :
Remarque :
-
Lorsque le système étudié n’est soumis qu’à son poids et à
l’action d’un fil est qu’il est immobile dans le référentiel lié au fil, alors
les deux forces ont même droite d’action est :
-
![]() et
T = P = 2 N
et
T = P = 2 N
-
Caractéristiques du poids ![]() :
:
|
|
Le point
d’application : |
G :
Centre d’inertie de l’objet
considéré |
|
La direction ; |
Verticale du lieu
passant par le point G. |
|
|
Le sens |
Du haut vers le bas |
|
|
L’intensité ou
valeur |
P
= m . g ≈ 2 N |
-
On peut en déduire les
caractéristiques de la tension
![]() du fil
du fil
|
|
Le point
d’application : |
A :
point d’attache du fil |
|
La direction ; |
Verticale du lieu
passant par le point G. |
|
|
Le sens |
Du bas vers le haut |
|
|
L’intensité ou
valeur |
T
= P = m . g ≈ 2 N |


-
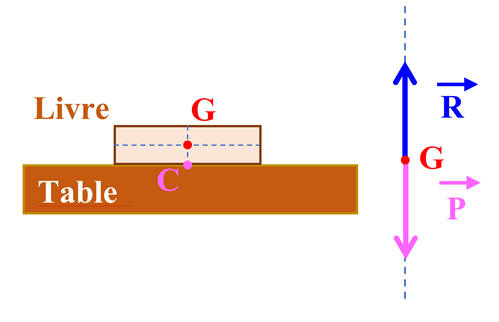
Exemple 1 : livre posé sur une table horizontale.
-
Le système étudié : Le livre.

-
Il est en interaction avec la Terre : Poids du livre
![]()
-
Il est en interaction avec la table : Réaction du support
![]()
-
Le système n’est soumis qu’à son poids
![]() et à la réaction du
support
et à la réaction du
support
![]() .
.
-
Comme il est immobile dans le référentiel lié au support, ici la
table :
-
Ces deux forces
![]() et
et
![]() ont même droite d’action et de plus :
ont même droite d’action et de plus :
-
![]()
-
Caractéristiques du poids :
![]()
|
|
Le point
d’application : |
G :
Centre d’inertie de l’objet
considéré |
|
La direction ; |
Verticale du lieu
passant par le point G. |
|
|
Le sens |
Du haut vers le bas |
|
|
L’intensité ou
valeur |
P
= m . g |
-
On peut en déduire les
caractéristiques de la réaction du support
![]() .
.
|
|
Le point
d’application : |
C :
Centre de la surface de contact |
|
La direction ; |
Verticale du lieu
passant par le point G. |
|
|
Le sens |
Du bas vers le haut |
|
|
L’intensité ou
valeur |
R
= P = m . g |
-
Schéma :
-
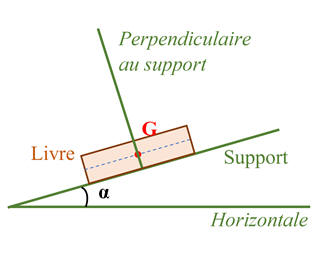
Exemple 2 : Livre posé sur un plan incliné.
-
Schéma de la situation :
-
Le système étudié : Le livre.
-
Il est en interaction avec la Terre : Poids du livre
![]()
-
Il est en interaction avec le support incliné : Réaction du
support ![]()
-
Le système n’est soumis qu’à son poids
![]() et à la réaction du
support
et à la réaction du
support
![]() .
.
-
Comme il est immobile dans le référentiel lié au support, ici la
table :
-
Ces deux forces
![]() et
et
![]() ont même droite d’action et de plus :
ont même droite d’action et de plus :
-
![]()
-
Caractéristiques du poids ![]() :
:
|
|
Le point
d’application : |
G :
Centre d’inertie de l’objet
considéré |
|
La direction ; |
Verticale du lieu
passant par le point G. |
|
|
Le sens |
Du haut vers le bas |
|
|
L’intensité ou
valeur |
P
= m . g |
-
On peut en déduire les
caractéristiques de la réaction du support ![]()
|
|
Le point
d’application : |
C :
Centre de la surface de contact |
|
La direction ; |
Verticale du lieu
passant par le point G. |
|
|
Le sens |
Du bas vers le haut |
|
|
L’intensité ou
valeur |
R’
= P = m . g |
-
Schéma :
-
La force modélisant l’action du support n’est pas perpendiculaire
au support.
-
Il y a des frottements entre les deux surfaces qui sont en
contact.
-
En l’absence de frottement, la force modélisant l’action du
support est perpendiculaire au support.
-
Dans ce cas
![]() et le livre glisse sur le plan incliné.
et le livre glisse sur le plan incliné.
1)-
Poids d’un corps sur la Terre et sur la Lune.
-
Le poids d’un corps sur la Lune peut s’identifier à la force
gravitationnelle exercée par la Lune sur l’objet
de masse m.
-
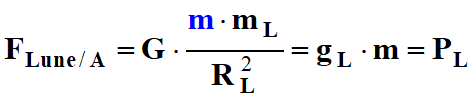
-
Un corps de masse
m n’a pas le même poids sur
-
Un objet de masse
m est environ six fois plus léger sur la
Lune que sur la Terre.
-
Comment peut-on retrouver ce résultat ?
-
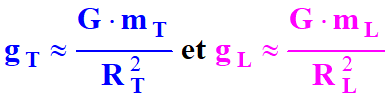
-
Il faut connaître le rayon de
-
R
L = 1,75
x
-
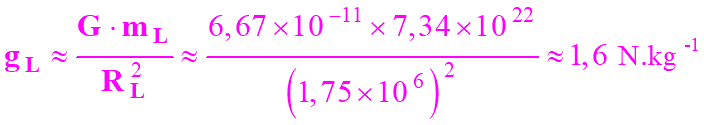
-
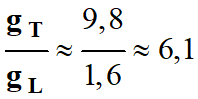
|
Modélisation d'une action mécanique Principe de l'interaction Exemples de forces |
|
1)-
Exercice 5 page 178 : Schématiser une force. 2)-
Exercice 6 page 178 : Classer des actions. 3)-
Exercice 9 page 178 : Caractériser l’interaction
gravitationnelle. 4)-
Exercice 11 page 179 : Calculer une force gravitationnelle. 5)-
Exercice 14 page 179 : Exploiter une relation vectotielle. 6)-
Exercice 16 page 179 : Calculer un poids sur la Lune : 7)-
Exercice 21 page 180 : Hubble et la Terre. 8)-
Exercice 22 page 180 : Côté maths. 9)-
Exercice 23 page 180 : Interaction gravitationnelle et poids. 10)-
Exercice 26 page 181 : J’ai pesée la Terre.
|
|
|