I- Introduction : Rappels et compléments.

1)- La célérité de la lumière.

-  En 1674, étudiant les éclipses de la planète Jupiter sur son satellite Io,

-  Le Danois Römer donne une première estimation de la vitesse de la lumière dans le vide.

-  La valeur fixée pour la vitesse de propagation de la lumière dans le vide est : 

-  C’est une constante Universelle.

-  Cette vitesse est une vitesse limite.

-  Aucun objet matériel ne peut atteindre cette vitesse dans le vide.

-  Dans les milieux transparents, la lumière se déplace moins vite que dans le vide.

-  La vitesse de la lumière dans l’air est peu différente de celle dans le vide.

-  Comme valeur approchée dans l’air et le vide, on choisit la valeur suivante :

2)- La lumière polychromatique et monochromatique.

a)-  La lumière blanche.

-  Déviation et dispersion de la lumière blanche par un prisme :

-  Le prisme dévie et décompose la lumière blanche en lumières colorées du rouge au violet.

-  C'est un phénomène de dispersion.

-  L'ensemble des couleurs obtenues constitue le spectre de la lumière blanche.

-  Le spectre est continu du rouge au violet.

-  La lumière blanche est constituée de plusieurs couleurs ou radiations : c’est une lumière polychromatique.

b)-  La lumière émise par un laser.

-  On éclaire une fente avec un faisceau laser de couleur rouge et on envoie le faisceau obtenu sur la face d’un prisme.

-  La lumière produite par un laser est constituée d’une seule radiation, elle est monochromatique.

c)-  Spectre continu.

-  La lumière blanche est un mélange de toutes les radiations visibles.

-  Spectre de la lumière blanche :

-  On est en présence d’un spectre continu.

-  De même, un corps chaud émet un spectre continu qui dépend de la température du corps chaud.

-  Plus le corps est chaud et plus le spectre s’étend vers le violet.

-  Exemple :  Spectre d’une lampe à incandescence dont on augmente la tension

d)-  Spectres de raies d’émission.

-  Exemple : Cas de la lampe à vapeur de mercure

-  On analyse à l’aide du spectroscope la lumière émise par une lampe à vapeur de mercure.

-  La lampe à vapeur de mercure contient des atomes (Hg) de mercure sous faible pression.

-  Ces atomes subissent des décharges électriques et sont excités.

-  Eux aussi subissent des décharges électriques et sont excités.

-  Spectre de la lampe à vapeur de mercure :

-  Les principales longueurs d’ondes (les plus visibles) :

-  615 nm, 568 nm, 546 nm, 542 nm, 436 nm,  405 nm.

-  Le spectre de cette lumière n'est pas continu.

-  On parle de spectre de raies d’émission

-  Chaque spectre est composé de raies colorées sur fond noir

-  Chaque raie colorée correspond à une radiation émise par l’entité.

-  Conclusion :

-  Le spectre obtenu est caractéristique des atomes du gaz qui émet les radiations.

-  Un spectre de raies constitue la signature d’un élément chimique et révèle sa présence.

-  Il permet d’identifier une entité chimique (atome ou ion).

II- La lumière et la dualité onde-particule.

1)- Modèle ondulatoire.

a)-  L’onde électromagnétique.

-  La lumière a une nature ondulatoire.

-  On parle de l’onde lumineuse.

-  L’onde lumineuse résulte de la propagation d’une perturbation électromagnétique dans les milieux transparents.

-  Les ondes lumineuses périodiques sont appelées des radiations.

-  Contrairement aux ondes mécaniques, la propagation des ondes lumineuses ne nécessite pas de support matériel.

-  La lumière peut se propager dans le vide.

-  La lumière est une onde transversale : la direction de propagation est perpendiculaire  à la direction de la perturbation.

-  L’onde lumineuse résulte de la propagation simultanée d’une perturbation électrique et d’une perturbation magnétique.

-  Dans le vide ou dans les milieux transparents homogènes, la lumière se propage en ligne droite.

-  Une radiation lumineuse est caractérisée par :

-  Sa fréquence ν (en Hz) ou sa période T (en s).

-  Sa longueur d’onde dans le vide λ₀.

-  Remarque :

-  La fréquence d’une radiation lumineuse ne dépend pas du milieu de propagation alors que la longueur d’onde dépend du milieu de propagation.

►  Relation fondamentale :

-  Remarque : pour les radiations lumineuses, on préfère utiliser la lettre grecque ‘’nu’’.

-  De manière générale, on caractérise une radiation lumineuse par sa longueur d’onde dans le vide.

-  Complément : l’œil humain n’est sensible qu’à certaines radiations lumineuses.

b)-  Les domaines d’application.

-  Le domaine de radiations lumineuses visibles s’étend de 400 nm (violet) à 780 nm (rouge).

-  Domaine de fréquences correspondant :

400 nm ≤ λ ≤ 780 nm

-  Spectre des ondes électromagnétiques :

-  Le spectre des ondes électromagnétiques est découpé, de façon arbitraire, en divers domaines.

►  Les sources de rayonnements :

-  Les corps célestes émettent des rayonnements dans divers domaines de longueurs d’onde.

-  Il est possible de caractériser certaines sources grâce aux types de rayonnements qu’elles émettent.

-  Le document suivant, donne des exemples de rayonnements dans divers domaines du spectre électromagnétique.

-  On remarque que la lumière visible ne représente qu’une infime partie du spectre électromagnétique.

-  Le rayonnement cosmique : il est constitué par des astroparticules, telles que des protons, des noyaux d’hélium, qui se propagent dans le vide interstellaire.

-   

-  Les objets célestes « chauds », tels que quasars, naines blanches, étoiles dites chaudes, émettent une grande part de leur rayonnement dans le domaine de l’ultraviolet.

-  Les objets « froids », comme les planètes, les étoiles jeunes, les nuages de poussières, émettent principalement dans le domaine de l’infrarouge.

2)- Modèle particulaire.

a)-  Historique.

-  Les phénomènes de diffraction et d’interférences de la lumière s’expliquent par ses propriétés ondulatoires. (Chap. N° 03 Propriétés des Ondes.)

-  En 1900, Max Planck fut conduit à postuler la quantification de l’énergie transportée par les ondes électromagnétiques.

-  Il postule que l’énergie électromagnétique ne peut s’échanger que par « paquets » ou quanta d’énergie.

-  En 1905, Albert Einstein émet l’idée que ces quanta d’énergie sont transportés par des particules.

-  On parle de modèle particulaire de la lumière.

-  En 1926, Gilbert Newton invente le mot « photons pour nommer ces quanta.

-  Les photons sont des particules de masse nulle et de charge nulle se propageant à la vitesse de la lumière.

b)-  Quantum d’énergie.

►  Énergie d’un photon :

-  L’énergie de la lumière est transportée par des photons qui présentent un aspect particulaire et un aspect ondulatoire.

-  L’énergie d’un photon est donnée par la relation :

-  E = h . ν

-  L’énergie E représente l’aspect particulaire du photon.

-  La fréquence n représente son aspect ondulatoire.

-  Pour une onde électromagnétique de fréquence ν et de longueur d’onde λ dans le vide,

-  On peut écrire :

III- L’interaction lumière-matière.

1)- Quantification de l’énergie des atomes.

a)-  Modèle de Bohr.

►  L’atome d’hydrogène :

-  Pour expliquer la présence de raies d’émission de l’atome d’hydrogène, Niels Bohr propose un modèle de structure de cet atome en introduisant la notion de niveau d’énergie.

-  Spectre d’émission de l’atome d’hydrogène :

►  En 1913, BOHR énonce les postulats suivants :

-  Les variations d’énergie d’un atome sont quantifiées.

-  L’atome ne peut exister que dans certains états d’énergie ou niveaux d’énergie bien définis.

-  Un photon de fréquence ν est émis lorsque l’atome effectue une transition d’un niveau d’énergie E_p vers un niveau inférieur E_n tel que : 

-  E_p - E_n = h . ν

-  Il résulte de ceci que les énergies d’un atome sont quantifiées.

-  Contrairement à l’énergie du système S = {planète + satellite},

-  Dans le cas de l’atome d’hydrogène : l’énergie du système  {proton + électron} ne peut prendre que certaines valeurs discrètes.

-  Le modèle planétaire de l’atome est à rejeter.

-  Ce qui est vrai pour l’atome d’hydrogène est vrai aussi pour les autres atomes.

-  Ceci reste valable pour les molécules qui sont des associations d’atomes.

-  Il en va de même pour les noyaux des atomes.

-  C’est pour cette raison que lors de la désexcitation d’un noyau, il y a émission d’un rayonnement γ.

-  L’énergie d‘un atome est quantifiée, l’énergie d’une molécule est quantifiée et l’énergie d’un noyau est quantifiée.

b)-  Diagramme de niveaux d’énergie.

-  Sur le diagramme de niveaux d’énergie d’un atome :

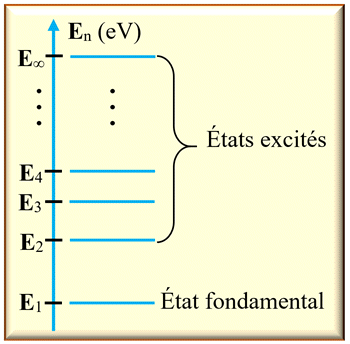
-  Le niveau d’énergie le plus bas correspond à l’état stable de l’atome.

-  On l’appelle l’état fondamental

-  Les autres niveaux correspondent à des états moins stables.

-  On les appelle les états excités.

-  L’état de plus haute énergie correspond à la perte d’un électron : l’atome est dit ionisé.

-  Par convention, son énergie est notée : E_∞ = 0 eV.

-  Comme les écarts entre les niveaux d’énergie sont faibles, on utilise l’électron-volt :

-  1 eV = 1,60 × 10^–19 J

-  Remarque : Les énergies des autres états sont négatives.

►  Schéma d’un diagramme d’énergie d’un atome :

2)- Émission et absorption de la lumière par un atome.

a)-  Introduction.

-  L’étude des spectres der raies d’émission et d’absorption des atomes a permis aux physiciens de comprendre l’interaction  lumière-matière.

►  Exemple de l’atome d’hydrogène :

-  Pour obtenir ce spectre, on soumet de l’hydrogène à des décharges électriques dans une ampoule.

-  Ce dispositif fournit de l’énergie aux atomes d’hydrogène.

-  Les atomes gagnent de l’énergie et se retrouvent dans un état excité instable.

-  Ils se désexcitent spontanément pour retrouver un état plus stable et une énergie plus basse.

-  Au cours de cette désexcitation, ils émettent de l’énergie lumineuse.

-  On observe un spectre de raies et non un spectre continu.

-  Les fréquences des radiations émises ne peuvent prendre que certaines valeurs particulières.

-  On dit que les fréquences sont quantifiées.

-  Ce spectre de raies est caractéristique de l’hydrogène, il permet de l’identifier.

-  Un atome d’hydrogène ne peut prendre que certains niveaux d’énergie.

-  Spectre d’émission :

-  Spectre d’absorption :

-  Un atome absorbe les radiations qu’il est capable d’émettre.

-  Au cours d’une transition entre deux états d’énergie E_initial et E_final le photon absorbé ou émis par un atome possède une énergie telle que :

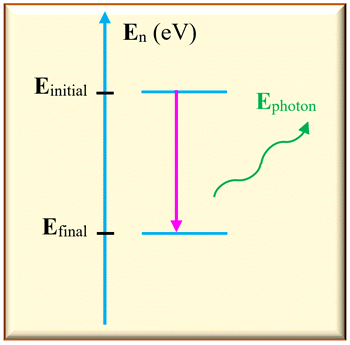
b)-  Émission de la lumière par un atome.

-  Dans ce cas, E_initial > E_final

-  L’atome perd de l’énergie en émettant un photon.

-  Sur un diagramme d’énergie, on représente cette transition par une flèche verticale orienté vers le bas.

-  L’énergie libérée est égale à la différence d’énergie entre les deux niveaux :

-  ΔE = | E_final – E_initial |

-  Cette énergie est transportée par un photon :

-  E_photon = ΔE = | E_final – E_initial | = h . ν

-  La fréquence ν découle de la différence d’énergie ΔE = | E_final – E_initial |

-  Si cette fréquence appartient au domaine du visible, elle correspond alors à une raie colorée dans le spectre d’émission de l’atome.

c)-  Absorption de la lumière par un atome.

-  Dans ce cas, E_initial < E_final

-  L’atome gagne de l’énergie en absorbant un photon.

-  Sur un diagramme d’énergie, on représente cette transition par une flèche verticale orienté vers le haut.

-  L’énergie absorbée est égale à la différence d’énergie entre les deux niveaux :

-  ΔE = | E_final – E_initial |

-  Cette énergie est transportée par un photon :

-  E_photon = ΔE = | E_final – E_initial | = h . ν

-  La fréquence ν découle de la différence d’énergie ΔE = | E_final – E_initial |

-  L’absorption d’énergie lumineuse par un atome ne peut se faire que si l’énergie du photon permet une transition d’un niveau E_initial à un niveau supérieur E_final tel que :

-  E_final – E_initial = h . ν

-  Si cette fréquence ν appartient au domaine du visible, elle correspond alors à une raie noire dans le spectre de la lumière blanche.

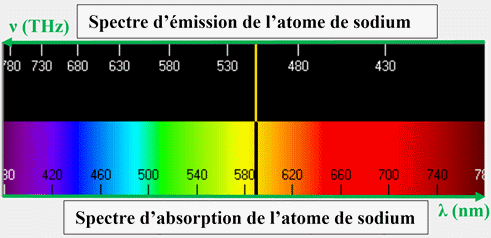
-  Exemple spectre d’émission et d’absorption de l’atome de sodium :

►  En conclusion :

-  Chaque entité chimique possède son propre diagramme d’énergie.

-  Il est ainsi possible d’identifier une entité chimique (atome, molécule ou ion) à partir de son spectre d’émission ou d’absorption.

-  Les radiations émises ou absorbées sont caractéristiques d’un atome car elles dépendent des niveaux d’énergie de cet atome.

-  L’atome d’hydrogène

IV- Applications.

1)- L’origine des raies du mercure.

-  La lumière émise par une lampe à vapeur de mercure est une lumière polychromatique.

-  Certaines de ces lampes sont utilisées comme lampe germicides car les radiations ultraviolettes qu’elles émettent détruisent les germes pathogènes.

-  Lampe à vapeur de mercure :

►  Spectres de la lampe à vapeur de mercure :

-  Les principales longueurs d’ondes (les plus visibles) :

-  615 nm, 568 nm, 546 nm, 542 nm, 436 nm,  405 nm.

►  Spectre d’émission du mercure et intensité lumineuse en fonction de la longueur d’onde :

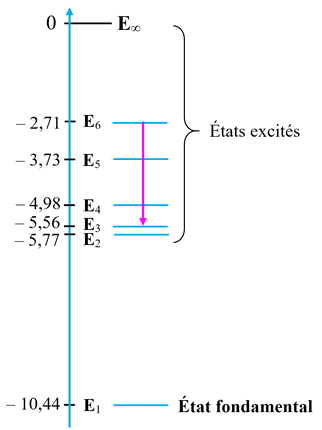
►  Diagramme de niveaux d’énergie simplifié de l’atome de mercure :

-  Tableau : Longueurs d’onde de quelques radiations émises par la lampe à vapeur de mercure :

  Quelques questions :

-  Protocole expérimental pour obtenir le spectre de la lumière émise par la lampe à vapeur de mercure.

-  Vérifier que le spectre obtenu est en accord avec les longueurs d’onde indiquées dans le tableau.

-  On étudie la transition du niveau d’énergie E₆ au niveau d’énergie E₃.

-  Identifier dans le spectre d’émission la raie correspondante.

-  La radiation émise par la lampe germicide a une longueur d’onde proche de 256 nm.

-  Sachant que cette radiation correspond à un retour à l’état fondamental de l’atome, de quelle transition s’agit-il ?

►  Réponses :

-  Montage expérimental :

►  Longueurs d’onde : Exploitation graphique

-  Étude de la transition du niveau d’énergie E₆ au niveau d’énergie E₃.

-  Dans ce cas, E_initial = E₆ < E_final = E₃

-  L’atome perd de l’énergie en émettant un photon.

-  L’énergie libérée est égale à la différence d’énergie entre les deux niveaux :

-  ΔE = | E_final – E_initial | = E₆ – E₃

-  Cette énergie est transportée par un photon :

-  E_photon = ΔE = | E_final – E_initial | = E₆ – E₃ = h . ν₆₃

-  La fréquence ν₆₃ découle de la différence d’énergie :

-  ΔE = | E_final – E_initial | = = E₆ – E₃

-   

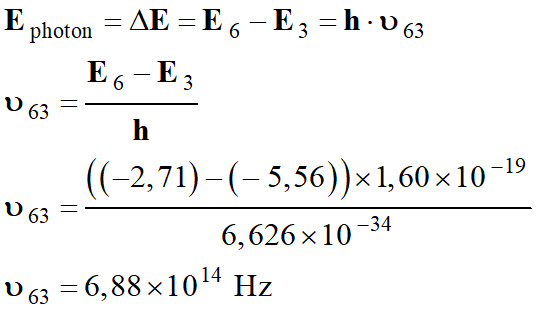
-  Longueur d’onde de la radiation :

-   

-  Il s’agit de la radiation bleue :

-  Transition qui donne la radiation de longueur d’onde :  λ = 256 nm.

-  Au plus l’écart est grand entre les niveaux d’énergie, au plus la fréquence est élevée et au plus la longueur d’onde est petite.

►  Première méthode :

-  On peut essayer la transition du niveau 6 au niveau 1 :

-   

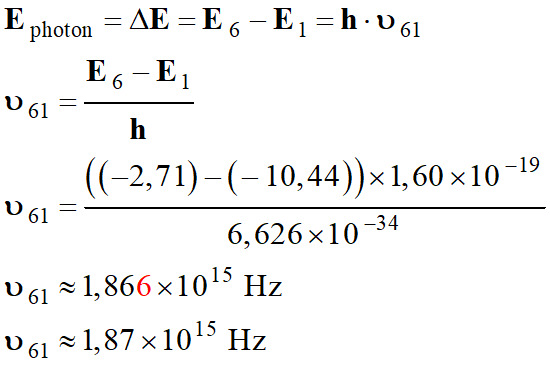
-  Longueur d’onde de la radiation :

-   

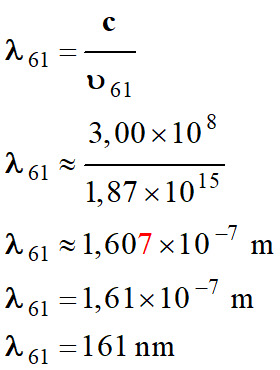
-  Il ne s’agit pas de cette transition :

-  Transition du niveau 5 au niveau 1 :

-   

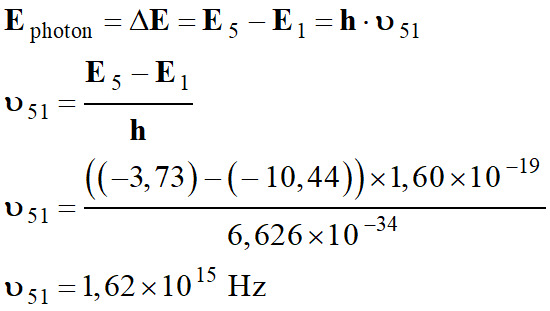
-  Longueur d’onde de la radiation :

-   

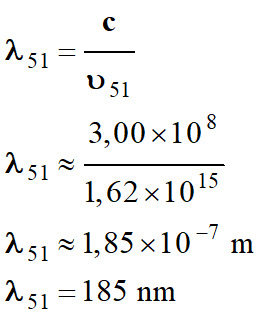
-  Il ne s’agit pas de cette transition :

-  Transition du niveau 4 au niveau 1 :

-   

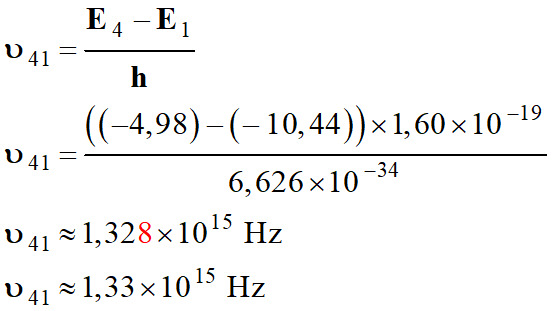
-  Longueur d’onde de la radiation :

-   

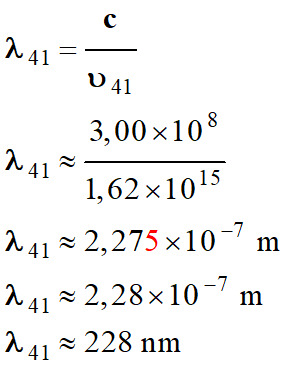
-  Il ne s’agit pas de la transition du niveau 4 au niveau 1, mais on se rapproche.

-  Transition du niveau 3 au niveau 1 :

-   

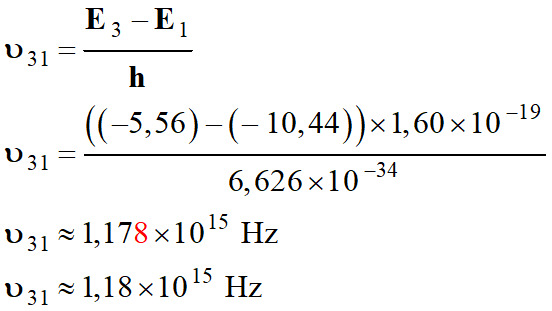
-  Longueur d’onde de la radiation :

-   

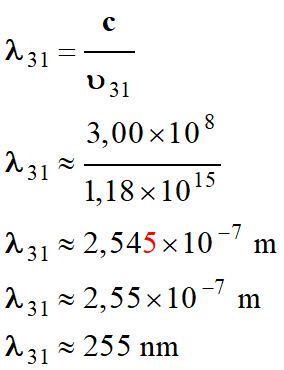
-  Il s’agit de la transition du niveau 3 au niveau 1.

►  Autre méthode (plus rapide) :

-  Soit E_n le niveau d’énergie initial.

-  Le niveau final est E₁, le niveau fondamental.

-  On connait la longueur d’onde de la radiation : λ_n1 ≈ 256 nm

-  Attention à l’unité d’énergie : 1 eV = 1,60 × 10^–19 J

-   

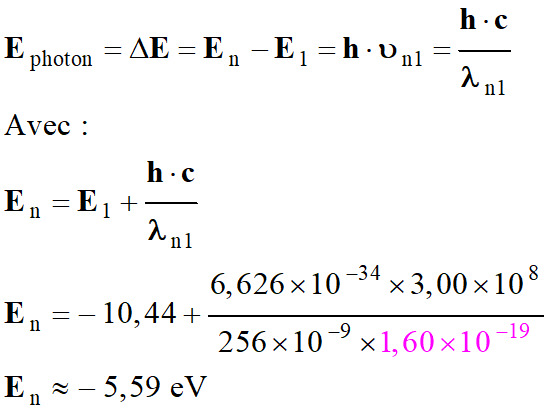
-  Il s’agit bien de la transition du niveau 3 au niveau 1.

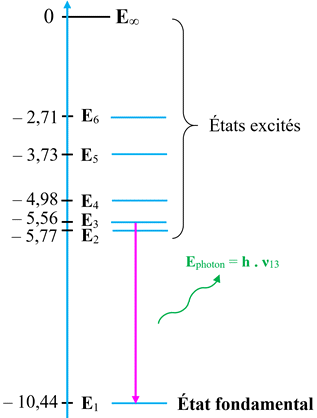
-  Cette radiation appartient au domaine des U.V.

2)- DM : Le cas de l’atome d’hydrogène.

CORRECTION

3)- QCM.

QCM réalisé avec le logiciel Questy

Pour s'auto-évaluer

La lumière et la dualité onde-corpuscule

L'interaction lumière-matière

Sour forme de tableau

4)- Exercices.