|
|
Aspects énergétiques Exercices |
|
|
|
|
1)- Exercice 02 page 268 : Utiliser les unités :
|
Utiliser les unités Si l'énergie cinétique EC est exprimée en joule (J) et la masse m en kilogramme (kg), en quelle unité faut-il exprimer la vitesse v ? |
|
Les unités : L'énergie cinétique :
|
2)- Exercice 04 page 268 : Calculer une énergie cinétique :
|
Calculer une énergie cinétique :
Une tortue de Horsfield pesant 1,50 kg se déplace à 0,25 km . h–1. - Calculer l’énergie cinétique de la tortue. |
|
Calculer une énergie cinétique :
-
Énergie cinétique de la tortue :
-
L’énergie cinétique caractérise un
système en mouvement.
-
Elle est
-
Proportionnelle à la masse m
du solide
-
Proportionnelle au carré de la
vitesse v du système.
-
Elle dépend du référentiel d’étude.
-
Le référentiel d’étude est un
référentiel terrestre.
-
|
3)- Exercice 06 page 268 : Calculer le travail d’une force :
|
Calculer le travail d’une force : À l’aide du schéma ci-dessous, calculer le travail de la force constante
lors de son déplacement du point d’application M de A à B. |
Calculer le travail d’une force :
-
Schéma :
-
Travail de la force constante lors de
son déplacement du point d’application
M de
A à
B :
-

![]()
4)- Exercice 08 page 268 : Calculer une variation d’énergie cinétique :
|
Calculer une variation d’énergie cinétique : Un point M se déplaçant de A vers B distants
de 5,0 m est soumis à une force constante de valeur F = 10 N. Schéma : - Calculer la variation d’énergie cinétique lors de ce déplacement
en supposant que les autres forces exercées sur le système ne travaillent pas. |
Calculer une variation d’énergie cinétique :
-
Variation d’énergie cinétique lors du
déplacement de la force
-
La variation de l’énergie cinétique
d’un système S en
mouvement, d’une position A à une
position B,
est égale à la somme des travaux de toutes les forces appliquées au système
S entre
A et
B :
-
-
Dans le cas présent, la seule force
qui travaille est la force
-
![]() de A à
B.
de A à
B.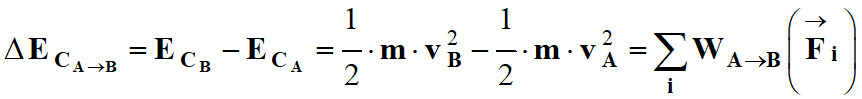
![]() :
:
![]()
5)- Exercice 10 page 269 : Caractériser le travail d’une force :
|
Caractériser le travail d’une force : Un solide glisse sur un plan incliné. 1.
Schématiser les deux situations et
représenter le poids du solide modélisé par un point. 2.
Préciser, pour chaque situation, si le
travail du poids est positif ou négatif. |
|
Un solide glisse sur un plan incliné. 1.
Schéma de chaque situation : a.
Situation a : le solide monte :
b.
Situation b : le solide descend.
2.
Type de travail du poids :
-
Le travail du poids :
-
Méthode 1 :
-
On considère le système
S, de masse m qui se
déplace du point A au
point B.
-
Le système
S est soumis à son poids
-
-
Si 0 ≤ α < 90 ° ,
alors cos α > 0 et
-
Si α = 90 ° , alors
cos α = 0 et
(le vecteur force est perpendiculaire au
déplacement).
-
Si 90 < α ≤ 180 ° ,
alors cos α < 0 et
-
le travail est résistant.
-
Méthode 2 : - Lorsque qu’un système S de masse m passe d’un point A à un point B, le travail du poids ne dépend que de l’altitude z A du point de départ et de l’altitude z
B du point
d’arrivée :
-
- Si z A > z B, l’altitude du système S a diminué : - le travail du poids est moteur. - Si z A < z B, l’altitude du système S a augmenté : - le travail du poids est résistant. - Si z A = z B, l’altitude du système S n’a pas changé : - le travail du poids est nul. a.
Situation a : le solide monte :
-
Schéma de la situation :
-
Méthode 1 :
-
-
Or : 90°
< α < 180° => cos
α
< 0
-
Dans ce cas le travail du poids est
négatif, il est résistant.
-
Méthode 2 :
-
-
Dans ce cas :
z
A < z
B, l’altitude du système S a augmenté :
-
Le travail du poids est
résistant.
-
Le travail du poids est négatif. b.
Situation b : le solide descend.
-
Schéma de la situation :
-
Méthode 1 :
-
-
Or : 0° <
α < 90° => cos
α
> 0 - Dans ce cas le travail du poids est positif, il est moteur.
-
Méthode 2 :
-
-
Dans ce cas :
z
A > z
B, l’altitude du système S a diminué :
-
Le travail du poids est
moteur.
-
Le travail du poids est
positif. |
6)- Exercice 11 page 269 : Calculer le travail d’une force de frottement :
|
Il est soumis à un ensemble de forces de valeurs constantes et schématisées ci-dessous à l’échelle. La force de traction
Schéma : 1.
Repérer la force de frottement parmi celles
représentées ci-dessus. 2.
Calculer le travail de la force de
frottement lors du déplacement de A à B. |
|
Calculer le travail d’une force de frottement : 1.
Repérage de la force de frottement.
-
Schéma :
-
-
-
-
2.
Travail de la force de frottement
-
Valeur de la force de frottement :
-
Les forces sont représentées à
l’échelle :
-
La force de traction
-
Échelle : 300 N ↔ 2,5 cm
-
Or la force de frottement
-
Valeur
F4 de la force
de frottement :
-
-
|
7)- Exercice 12 page 269 : Calculer une altitude :
|
Calculer une altitude : Un pot de fleurs est posé sur un poteau. -
Calculer la hauteur à laquelle se trouve le pot de
fleurs. -
Données : g = 10 N . kg–1 -
Schéma :
|
|
Calculer une altitude : Hauteur à laquelle se trouve le pot de fleurs :
-
Schéma :
-
Expression de l’énergie potentielle
de pesanteur en fonction de l’altitude
z :
-
EP =
m .
g . z
-
À l’altitude
z = 0 m , EP =
0 J.
-
L’axe
Oz est orienté vers le
haut.
-
À l’altitude du pot :
zpot = ? , EPpot =
45 J.
-
Schéma :
-
Expression de l’énergie potentielle
de pesanteur du pot :
-
EPpot =
m . g . zpot
-
Altitude du pot :
zpot
-
-
Hauteur
h à laquelle se trouve le
pot de fleurs :
-
h =
zpot –
z0 ≈ 1,5 m
|
8)-Exercice 14 page 269 : Exprimer une énergie mécanique :
|
Exprimer une énergie mécanique : Un fruit, accroché à un arbre, tombe sur le sol. On néglige l’action de l’air sur le fruit au cours de la chute. 1.
Dans un référentiel terrestre exprimer
l’énergie mécanique du fruit : a.
Lorsqu’il est accroché dans l’arbre ; b.
Juste avant qu’il touche le sol. 2. Indiquer pourquoi on peut considérer que cette énergie est constante lors du mouvement du fruit. |
Exprimer une énergie mécanique :
a.
Position 1 : Le fruit est accroché dans
l’arbre :
-
Le fruit de masse
m st à l’altitude z :
-
Son énergie potentielle de
pesanteur :
-
EParbre =
m .
g .
z
-
Le fruit est accroché, sa vitesse est
nulle :
-
vz = 0 m . s–1
-
Son énergie cinétique :
-
-
ECarbre =
0 J
-
Énergie mécanique du fruit :
-
Emarbre =
ECarbre +
EParbre
-
Emarbre =
m .
g .
z b.
Position 2 : le fruit juste avant qu’il
touche le sol.
-
Au niveau du sol :
-
Son altitude
zsol = 0 m
-
Son énergie potentielle de
pesanteur :
-
EPsol =
m .
g .
zsol
-
EPsol =
0 J
-
Il possède la vitesse
vsol.
-
Son énergie cinétique
au niveau du sol :
-
-
Énergie mécanique du fruit au niveau
du sol :
-
Emsol =
ECsol +
EPsol
-
2.
Évolution de l’énergie mécanique de la pomme
lors de la chute.
-
On néglige l’action de l’air sur le
fruit au cours de la chute.
-
En conséquence, le fruit est en chute
libre.
-
Il n’est soumis qu’à l’action de son
poids
-
Le poids est une force conservative.
-
L’énergie mécanique du fruit se
conserve au cours de la chute.
-
Lors de la chute libre, l’altitude du
système diminue et son énergie potentielle diminue.
-
Simultanément, sa vitesse augmente et
de ce fait, son énergie cinétique augmente.
-
Au cours du mouvement, l’énergie
potentielle se transforme en énergie cinétique.
-
L’énergie mécanique d’un système
soumis uniquement à son poids reste constante.
![]()
![]()
![]()
![]() .
.![]()
10)- Exercice 19 Page 270 : Freinage d’un véhicule :
|
Un véhicule de masse m = 1000 kg est en mouvement sur une
route horizontale et rectiligne à la vitesse de valeur v = 80
km . h–1. Sous l’action exclusive de son système de freinage, le véhicule
s’arrête après avoir parcouru une distance AB = 50 m.
1.
Identifier les forces
2.
Donner l’expression du travail de ces
forces, considérées comme constantes lors du freinage entre A
et B. 3. Par application du théorème de l’énergie cinétique, calculer la valeur de la force responsable du freinage. |
|
Freinage d’un véhicule :
-
Le système étudié : le véhicule :
-
Le référentiel d’étude : le sol
(référentiel terrestre)
-
Masse du système :
-
m = 1000 kg
-
Vitesse du système dans le
référentiel terrestre :
-
v = 80 km . h–1
-
Schéma de la situation :
1.
Identification des différentes forces :
-
-
- 2.
Expression du travail des différentes forces
lors du freinage entre A et B.
-
Travail de la force
-
-
Car
-
Travail de la force
-
-
Car
-
Travail de la force
-
3.
Valeur de la force responsable du freinage.
-
On applique de théorème de l’énergie
cinétique au système par rapport au référentiel d’étude. - La variation de l’énergie cinétique d’un système S en mouvement, d’une position A à une position B,
est égale à la somme des travaux de toutes les forces appliquées
au système S entre
A et
B :
-
-
Position
A :
-
vA = 80 km . h–1
-
Position
B :
-
vB
= 0,0 km . h–1
-
Somme des travaux des différentes
forces appliquées au système :
-
-
En conséquence :
-
-
Application numérique :
-
|
11)-Exercice 21 page 270 : Chute libre ? :
|
Chute libre ? On a réalisé le pointage vidéo d’une balle de golf en chute,
lâchée sans vitesse initiale. Le traitement des données avec un logiciel adapté a conduit aux
mesures suivantes :
1.
Force et
travail : a.
Dans l’hypothèse d’une chute libre, à quelle
force est soumise la balle lors de sa chute ? b.
Déterminer le travail de cette force entre
les positions M4 et M8. 2.
Calculer les énergies cinétiques EC4 et
EC8 de
la balle aux positions M4 et M8. 3. Comparer la variation d’énergie cinétique de la balle, entre les positions M4 et M8, au travail de la force qui s’applique sur elle dans l’hypothèse d’une chute libre. Expliquer la différence
observée.
-
Données :
-
g = 9,81 N . kg–1.
-
Masse de la balle :
-
m = 46 g. |
|
Chute libre ?
-
Système étudié : la balle de golf.
-
Masse de la balle :
-
m = 46 g.
-
Bilan des forces si chute libre :
-
Le poids
-
Référentiel terrestre.
-
g = 9,81 N . kg–1
-
Tableau de valeurs :
1.
Force et travail : a.
Bilan des forces dans l’hypothèse d’une
chute libre :
-
La balle est soumise à son poids :
b.
Travail de cette force entre les positions
M4 et M8.
-
Comme on donne les altitudes des
points M4 et M8
-
On utilise la relation suivante :
-
-
Application numérique :
-
-
Remarque : Le travail du poids 2.
Valeurs des énergies cinétiques EC4 et
EC8 de
la balle aux positions M4 et M8.
-
Valeur de
EC4 :
-
-
Valeur de
EC8 :
-
au travail de la force qui
s’applique sur elle dans l’hypothèse d’une chute libre.
-
Variation d’énergie cinétique de la
balle :
-
-
Comparaison de
ΔEC4→8 et
-
Remarque :
-
ΔEC4→8 <
-
L’énergie mécanique du système ne se
conserve pas.
-
Lors de son déplacement, la balle est
soumise à une force de frottement.
-
Cette force de frottement
-
Son travail est négatif.
-
La balle n’est pas en chute libre. |
12)- Exercice 25 page 271 : Énergie cinétique d’une balle qui chute :
|
Énergie cinétique d’une balle qui chute : On mesure la valeur de la vitesse de chute v acquise par une balle lestée de masse m = 300,0 g qui tombe d’une hauteur h =
2,00 m. La mesure est réalisée 10 fois et les résultats sont consignés
dans un tableau ci-dessous :
1.
Les
valeurs moyennes : a.
Calculer la valeur moyenne
b.
Calculer alors l’énergie cinétique moyenne
2.
Évaluer l’incertitude-type u (v)
sur la valeur de la vitesse. 3.
Évaluer l’incertitude-type sur l’énergie
cinétique donnée par la relation suivante :
-
- Exprimer EC sous forme d’encadrement.
|
|
Énergie cinétique d’une balle qui chute :
-
Tableau de valeurs :
1.
Les valeurs moyennes : a.
Valeur moyenne
-
Remarque :
-
Le nombre de mesures :
-
- b.
Valeur de l’énergie cinétique moyenne
-
2.
Incertitude-type u (v) sur la
valeur de la vitesse.
-
La variance de la valeur de la
vitesse : var (v)
-
La variance peut se calculer à partir
de la formule de Kœnig :
-
-
Valeur de la variance :
-
Tableau réalisé avec Excel :
- Taper la formule suivante et choisir la plage de cellules
concernées. -
Formule : =VAR.P.N (L2 : P3) -
var (v) ≈ 2,160
×10–4 m2 . s–2
-
var (v) ≈ 2,16 ×10–4
m2 . s–2
-
Écart-type de la valeur de la
vitesse :
-
Le calcul de l’écart type découle de
celui de la variance car l’écart type est égal à la racine carrée de la variance :
-
- Taper la formule suivante et choisir la plage de cellules
concernées. - Formule : =ECARTYPE.PEARSON (L2 : P3)
-
Incertitude-type u (v)
sur la valeur de la vitesse :
-
L’incertitude-type u (v)
est arrondie généralement par excès en ne conservant qu’un seul chiffre significatif :
-
u (v) ≈ 0,005 m . s–1. 3.
Incertitude-type sur l’énergie cinétique
donnée par la relation suivante :
-
-
-
On arrondit par excès.
-
Expression de
EC sous forme d’encadrement :
-
|
|
|