CabriJava aide

Figure gnomon.fig

Applet created on 10/10/05 by CG with CabriJava

-     Soit α l’angle formé par les deux verticales et β l’angle formé par le gnomon à Alexandrie et les rayons du soleil.

-     Les représenter sur le schéma. Quelle relation existe-t-il entre ces deux angles.

-     Les droites (D), (D') et (D'') étant parallèles α = β

-     Calculer β en utilisant les relations trigonométriques dans un triangle rectangle et en déduire la valeur de α.

-     On travaille dans le triangle ABC rectangle en A  :

-    

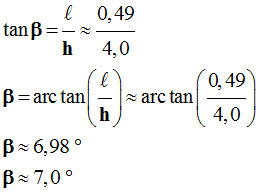
-     Les relevés cadastraux de l’époque d’Ératosthène indiquaient 5000 stades pour la distance entre Syène et Alexandrie.

-      Sachant que 1 stade = 157 m , calculer la distance d entre ces deux villes en mètres.

-      Vérifier la valeur trouvée à l’aide de la carte fournie (document 1). Conclusion.

-      Distance d entre les deux villes en mètres  :

-      d = 5000 x 157 

-      d = 7,85 x 10⁵ m

-      Distance d_p entre les deux villes en mètres  à l'aide du plan :

-      Distance d_p entre les deux villes en mètres  à l'aide du plan :

-     Incertitude relative :

-    

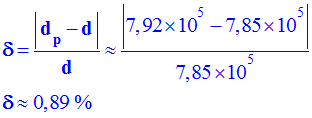
-     Le résultat trouvé à l'aide de la carte  (d_p = 792 km) est en accord avec celui trouvé précédemment d = 785 km).

-     Connaissant l’angle α et la distance d séparant les deux villes, en déduire la circonférence de la Terre (en expliquant le calcul).

-     Circonférence de la Terre :

-     

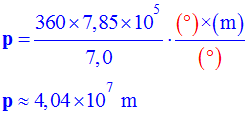
-     En déduire la valeur du rayon R_E de la Terre par la méthode d’Ératosthène.

ʘ    On rappelle que pour un cercle de rayon R, le périmètre est p = 2 π R.

-     Rayon de la Terre :

-     

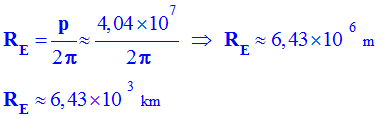
-     Comparer cette valeur avec celle actuellement admise de 6378 km .

-     Incertitude relative :

-     Déterminer la valeur de l’incertitude relative 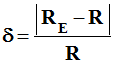 sur la mesure. Conclusion.

-     Incertitude relative :

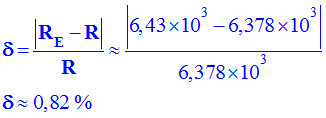
Cette méthode permet de trouver le rayon de la Terre avec une bonne précision (de l'ordre de 1 %).