|
Phys. N° 13 |
Oscillateurs mécaniques. Cours. |
|
|
|
|
Programme 2012 : Physique et Chimie Programme 2020 : Physique et Chimie |
Pour
aller plus loin :
Mots clés : Système oscillant ; pendule simple ; pendule élastique ; résonance ;
...
I- Notion de système oscillant.
- Une balançoire, une masse accrochée à un ressort, une masse accrochée à un fil sont des systèmes oscillants mécaniques.
2)- Particularité d’un système oscillant.
- Un système oscillant possède une énergie potentielle minimale.
- Lorsqu’on écarte le système de son état d’équilibre et qu’on l’abandonne à lui-même, il effectue des oscillations libres autour de son état d’équilibre.
- On appelle oscillation la variation cyclique autour d’une valeur moyenne d’une grandeur caractérisant l’état du système.
- En physique, l’amplitude désigne la moitié de l’écart entre la valeur maximale et la valeur minimale de la fonction.
- C’est une grandeur positive :
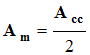
a)- Définition.
- Un pendule pesant est un système oscillant en rotation autour d’un axe horizontal.
- Écarté de sa position d’équilibre, il oscille autour de cette position sous la seule action de son poids.
- Une balançoire constitue un pendule pesant.
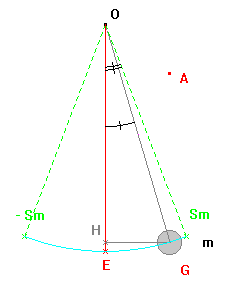
- Exemple de pendule pesant : pendule constitué d’un disque de masse m surmonté d’une tige de masse négligeable devant celle du disque.
- L’ensemble peut pivoter librement autour d’un axe horizontal.
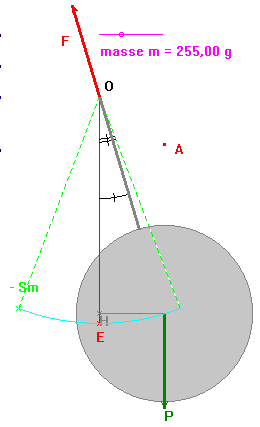
b)- Action des forces.
-
Le pendule est soumis à deux forces : son poids
et la force
exercée par l’axe de rotation.
- Cette dernière n’a aucun effet sur le mouvement du pendule (sa ligne d’action passe par l’axe de rotation).
- Lorsque le pendule est en équilibre, la ligne d’action du poids passe par l’axe de rotation.
- Pour cette position particulière, le poids n’a aucune action sur la rotation du pendule.
- Si l’on écarte le pendule de cette position, la ligne d’action du poids ne passe plus par l’axe de rotation et
- le poids a une action sur la rotation du pendule, le pendule tend à revenir vers sa position d’équilibre.
- Un pendule est en équilibre stable lorsque le centre d’inertie est sur la verticale passant par l’axe de rotation et est situé en dessous de l’axe de rotation.
Animation : CABRIJAVA.
c)- Grandeurs caractéristiques.
- On peut repérer à chaque instant l’abscisse angulaire θ (t) :
- c’est l’angle formé par le pendule à la date t et le pendule à l’équilibre.
- C’est une grandeur algébrique.
- L’amplitude θm
est la valeur absolue de l’abscisse angulaire maximale.- C’est une grandeur positive.
- La période est la durée d’une oscillation complète : un aller-retour.
d)- Isochronisme des petites oscillations.
- La période d’un pendule pesant ne dépend pas de l’amplitude θm des oscillations si celle-ci reste inférieure à 20 ° ;
- c’est l’isochronisme des petites oscillations.
e)- Amortissement des oscillations.
- Les forces de frottement qui s’exercent sur le pendule provoquent une diminution de l’amplitude des oscillations.
- Le mouvement est amorti et le phénomène n’est pas rigoureusement périodique.
- Quand l’amortissement est faible, le régime est pseudo-périodique est possède une pseudo-période qui est voisine de la période propre du pendule.
- Quand on augmente l’amortissement, le pendule passe d’un régime pseudo-périodique à un régime apériodique ( il n’oscille plus).
1)- Le modèle du pendule simple.
- Un pendule simple est constitué d’un objet de petites dimensions suspendu à un fil de masse négligeable.
- La masse du fil est négligeable devant la masse m de l’objet et la longueur du fil ℓfil > 10 R.
- R représente le rayon d’un objet sphérique.
2)- Étude expérimentale du pendule simple : TP Physique N° 13.
- La période propre d’un pendule simple est indépendante de la masse m.
- Elle varie dans le même sens que la longueur du fil et en sens inverse de la valeur du champ de pesanteur.
- La période propre des oscillations de faibles amplitudes dépend :
- De la longueur ℓ du pendule simple
- De la valeur g du champ de gravitation.
- Les grandeurs ℓ et g sont des paramètres spécifiques.
- Remarque : la période propre T0 ne dépend pas de la masse m du solide.
- Expression de la période :
- 
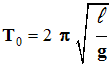
- analyse dimensionnelle :
- 
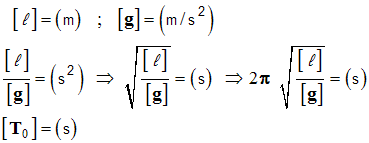
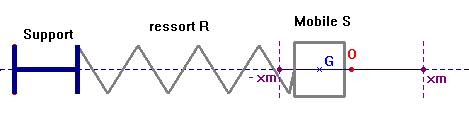
1)- Force de rappel exercée par un ressort.
- Un ressort à spires non jointives exerce une force proportionnelle à la longueur du déplacement de l’extrémité libre du ressort.
Animation : CABRIJAVA.
- O représente la position de l’extrémité du ressort à l’équilibre ( origine de l’axe) et M représente la position de l’extrémité du ressort lorsqu’il est excité.
- Force de rappel
exercée par le ressort sur le solide
S :
- expression vectorielle :
- Valeur de la tension : F = k . | x |
- k représente la raideur du ressort à spires non jointives en N / m,
- x représente l’abscisse de l’allongement du ressort par rapport à sa position d’équilibre,
- F représente la valeur de la tension en N.
2)- Expression de la période de la période propre de l’oscillateur élastique.
a)- Période de l’oscillateur et masse du solide S.
- On remarque que la période T0 augmente lorsque la valeur de la masse augmente.
- La période T0 diminue lorsque la valeur de la raideur du ressort augmente.
- Expression de la période propre du pendule élastique :
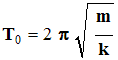
b)- Analyse dimensionnelle.
- Montrer que cette relation a bien la dimension d’un temps.
-
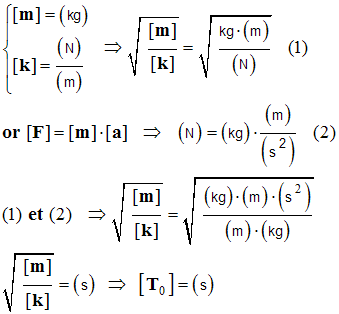
3)- étude dynamique du système solide-ressort.
- Écarté de sa position d’équilibre et abandonné à lui-même, le solide S, en translation effectue des oscillations libres.
- Le mobile S se déplace sur coussin d’air et on peut considérer que les frottements sont négligeables.
- Le système {support - ressort - solide } constitue un oscillateur libre.
- L’étude de la variation de l’élongation x en fonction du temps t, x = f (t), montre que les oscillations sont sinusoïdales.
- Le mobile effectue des oscillations périodiques autour de la position d’équilibre.
- Étude du système à l’instant t.
Animation : CABRIJAVA.
- Le repère choisi :
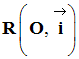O
représente la projection de G à l’équilibre sur
l’axe x’Ox
et M
représente la projection de G à l’instant t.
- Bilan des forces :
- On se place dans le cas où les forces de frottement sont négligeables devant les autres forces.
|
Le mobile est soumis : |
|
|
|
|
- Dans le référentiel terrestre supposé galiléen, on peut appliquer le théorème du centre d’inertie :
- 
- Projetons la relation sur l’axe x’Ox :
- 
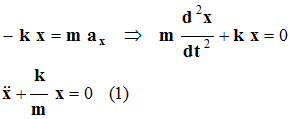
- Le mouvement de l’oscillateur élastique libre non amorti vérifie cette équation différentielle.
- On parle d’oscillateur harmonique.
- Remarque : l’équation différentielle se présente comme une relation du premier degré entre la fonction de x (t) et certaines de ses dérivées.
- Cette équation différentielle est qualifiée de linéaire car elle présente cette propriété (oscillateur linéaire).
- La solution générale de l’équation est du type :
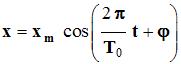
- La grandeur x
m représente l’amplitude des oscillations, T0 représente la période propre des oscillations et φ la phase à l’origine des dates.- La période propre est liée aux caractéristiques du système mécanique.
- La solution vérifie l’équation (1) si
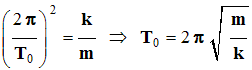
Étude expérimentale du pendule élastique : TP Physique N° 13.
IV- Phénomène de résonance.
1)- Les oscillations forcées. Définition.
|
Définition des oscillations forcées : - Un système oscillant de fréquence propre f0 que l’on appelle le résonateur, subit des oscillations forcées, s’il oscille à la fréquence f imposée par l’excitateur. |
- Le haut-parleur est un exemple d’oscillations forcées.
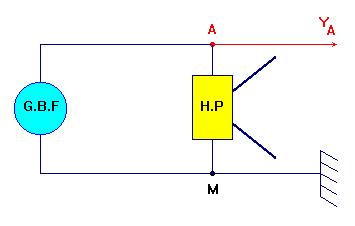
- On accroche un pendule élastique à la membrane du H.P.
- On règle le G.B.F sur 10 x mHz et on affiche 500.
- Puis on détermine la valeur de la fréquence de vibration du dispositif.
- Schéma du montage.
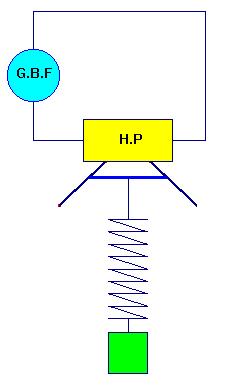
- Le pendule élastique effectue des oscillations forcées à la fréquence f imposée par le G.B.F.
on augmente
lentement la fréquence de l’excitateur et on observe le comportement du
pendule élastique (le résonateur).
- L’amplitude des oscillations du pendule élastique (résonateur) dépend de la fréquence f de l’excitateur.
- Cette amplitude est maximale lorsque f0 ≈ f.
- On dit que le résonateur entre en résonance.
- Un
système oscillant entre en résonance lorsqu’il est excité à une fréquence
voisine de sa fréquence propre f0.
- à
la résonance, l’amplitude des oscillations est maximale.
- La résonance se manifeste
de manière importante lorsque le système est peu amorti.
- Courbe de résonance.
- Exemple :
- Remarque :
si l’amortissement est faible, la résonance est aiguë,
- Si l’amortissement est
fort, la résonance est floue.
- Si
l’amortissement est faible fR
≈
f0 avec
fR
< f0.
Animation : résonnance d'un pendule élastique.
V- Applications.
