|
Contrôle N° 04 Sciences physiques, année 2003 Terminale S énoncé et correction |
|
|
I-
Le circuit (L, C).
Un condensateur, de bornes A et B et de capacité C = 22 μF est préalablement chargé sous une tension E = 4,0 V.
Il est branché, à un instant pris pour origine des dates, aux bornes M et N d’une bobine d’inductance L = 10 mH et de résistance quasi nulle.
Un oscilloscope à mémoire permet d’enregistrer la tension uAB = uC aux bornes du condensateur et de visualiser les oscillations électriques obtenues.
1)- Réaliser un schéma du montage décrit. Indiquer le mode de
branchement de l’oscilloscope. Donner l’allure de l’oscillogramme
obtenu.
-
Schéma du montage :
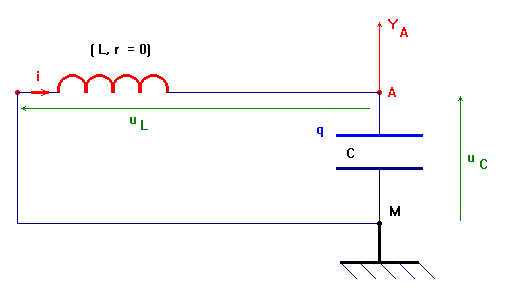
-
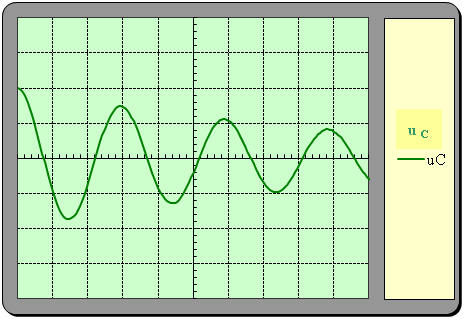
Allure de l’oscillogramme obtenu :
-
Durée de balayage : 1ms / div et
Sensibilité verticale : 2 V / div
2)- Établir l’équation différentielle régissant l’évolution de la
tension uC lors des oscillations électriques.
-
Équation différentielle :
-
Avec l’orientation choisie :
-
Tension aux bornes du condensateur :
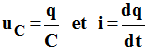
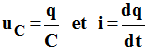
-
On tire de ces expressions :
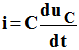
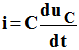
-
Tension aux bornes de la bobine idéale :
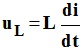
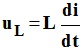
-
L’additivité des tensions appliquée au circuit précédent :
-
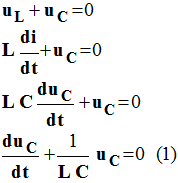
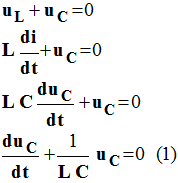
3)- Étude analytique :
a)-
vérifier que la
fonction :
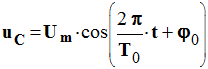 décrit la variation
de la tension uC au cours du temps.
décrit la variation
de la tension uC au cours du temps.
-
Vérification de la solution :
-
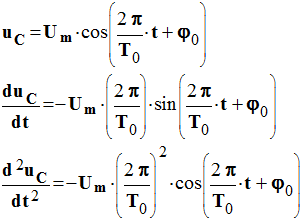
-
On tire de ceci :
-
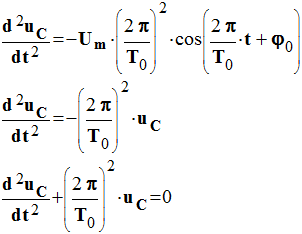
-
La tension u C vérifie l’équation (1) si :
-
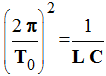 .
.
-
La grandeur T0 représente la période de la
tension et L et C sont les caractéristiques du circuit.
b)- Exprimer et calculer la période T0 des oscillations électriques.
-
Période des oscillations du circuit :
-
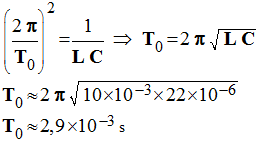
c)- Que représentent les grandeurs Um et φ0 ? Déterminer leurs valeurs.
-
La grandeur Um représente l’amplitude de la
tension uC. C’est une grandeur positive (V).
-
La grandeur φ0 représente la phase à l’origine
des dates (rad).
-
On utilise les conditions initiales :
-
Au temps t = 0 s, i (0) = 0 et uC
(0) = E.
-
Expression de l’intensité en fonction du temps :
-
On connaît :
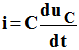 et
et
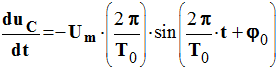
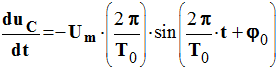
-
On tire :
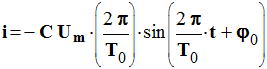
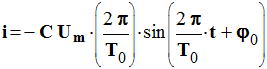
-
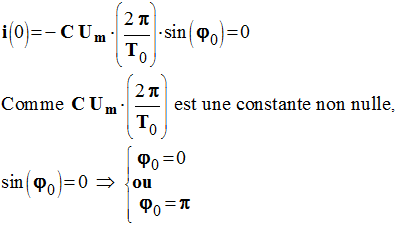
4)- En réalité, les oscillations sont amorties.
a)- Quelle est la raison principale de l’amortissement ?
- La raison principale de l’amortissement est la présence d’une résistance dans le circuit (les fils de connexion)
b)- Indiquer alors l’allure de la courbe donnant les variations de la tension uC en fonction du temps.
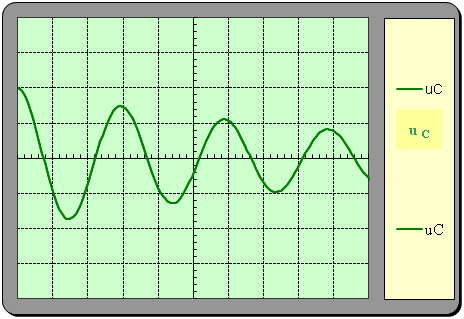
Ou
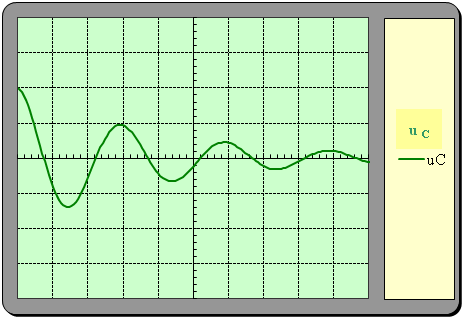
II-
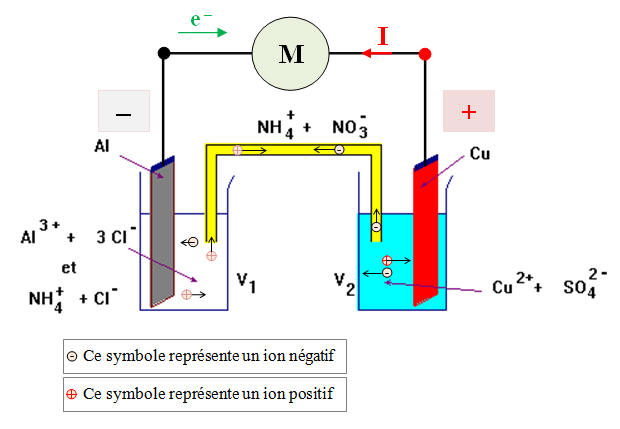
Pile aluminium – cuivre.
On considère la pile représentée ci-dessous.
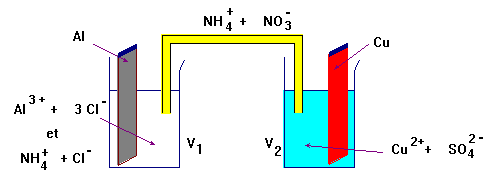
Les volumes des solutions dans les deux demi-piles valent : V 1 = V 2 = 50 mL.
[Cu 2+]
i = 0,10 mol / L et [Al 3+] i
= 0,10 mol / L
Lorsqu’on branche un voltmètre électronique avec sa borne COM reliée à l’électrode d’aluminium, on mesure une différence de potentiel U = + 1,6 V.
1)- Quelle est la polarité de la pile ?
- Polarité de la pile :
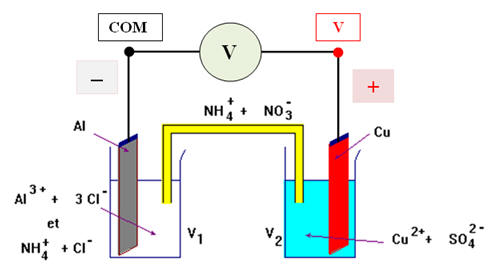
2)- On relie la pile à un petit moteur électrique.
a)- Faire un schéma du dispositif. Indiquer le sens du courant dans le circuit.
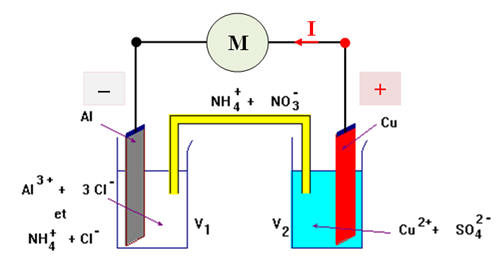
b)- Préciser la nature et le sens des porteurs de charges dans ce circuit.
- Dans les fils électriques ce sont les électrons qui se déplacent. De l’électrode d’aluminium (borne –) vers l’électrode de cuivre (borne +).
- Dans les solutions et le pont salin, ce sont les ions présents dans les solutions qui se déplacent.
3)- Donner les équations des réactions qui se produisent aux
électrodes. Préciser où ont lieu l’oxydation et la réduction. Identifier
l’anode et la cathode.
- Réactions aux électrodes :
- Il se produit une réduction à la borne positive (+).
- La réduction se produit à la cathode qui est dans ce cas l’électrode positive.
- Cette réaction consomme des électrons : Cu 2+ (aq) + 2 e – = Cu (s)
- Il se produit une oxydation à la borne négative (-).
- L’oxydation se produit à l’anode qui est dans ce cas l’électrode négative.
- Cette réaction produit des électrons : Al (s) = Al 3+ (aq) + 3 e –
4)- Écrire l’équation de l’oxydoréduction spontanée qui se produit
dans la pile.
|
Réduction |
3 ( |
Cu 2+ (aq) |
+ |
2 e – |
= |
Cu (s) |
) |
|
|
|
Oxydation |
|
|
2 ( |
Al (s) |
= |
3 e – |
+ |
Al 3+ (aq) |
) |
|
Oxydoréduction |
|
3 Cu 2+
(aq |
+ |
2 Al (s) |
→ |
3 Cu (s) |
+ |
2 Al 3+ (aq) |
|
5)- La pile fonctionne pendant 1,0 heure en débitant un courant
d’intensité 50 mA.
a)- Calculer la variation Δm (Al) de la masse d’aluminium métallique.
- Variation de la masse d’aluminium métallique.
- Au cours de la réaction d’oxydoréduction, de l’aluminium métallique disparaît pour donner des ions aluminium III.
- En conséquence, la masse de l’électrode d’aluminium diminue.
- Dans un premier temps, on va calculer la quantité d’électricité débité par la pile :
- Quantité d’électricité Q débitée par la pile :
-


- Quantité de matière d’électrons n (e – ) échangés.
-
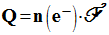
-
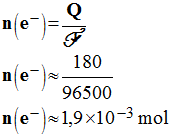
|
Équation |
Al (s) |
= |
Al 3+ (aq) |
+ 3 e – |
|
|
état |
Avancement x (mol) |
mol |
|
mol |
mol |
|
État initial (mol) |
0 |
n
1 |
|
C
i
.V |
0 |
|
Au bout de la durée
Δt |
x |
n
1 - x |
|
C
i
.V - x |
3 x |
- Connaissant la quantité de matière d’électrons n (e – ) échangés, on peut en déduire la valeur de x.
-
n (e
– ) = 3 x
=>
x ≈ 6,2
× 10
– 4
mol ou 6,3
× 10
– 4
mol (si on fait le calcul
avec la valeur arrondit).
- À l’instant initial, la masse de l’électrode d’aluminium vaut m i et après la durée Δt = 1,0 h, elle vaut m f :
-
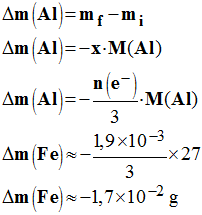
b)- Calculer la variation de concentration Δ[Cu 2+] en ions cuivre II Cu 2+.
|
Équation |
Cu 2+ (aq) |
+ |
3 e – |
= |
Cu (s) |
|
|
état |
Avancement x (mol) |
mol |
|
mol |
|
mol |
|
État initial (mol) |
0 |
C
i
.V |
|
0 |
|
n
1 |
|
Au bout de la durée
Δt |
x |
C
i
.V - x
|
|
2 x |
|
n
1 - x |
- Lorsque la pile débile, la concentration en ions cuivre II diminue.
- Au bout de la durée Δt, elle a diminué de x et le volume de la solution n’a pas varié.
-
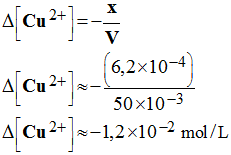
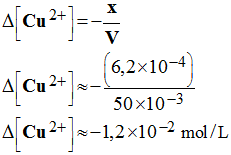
On donne : F = 96500 C / mol et M (Al) = 27 g / mol