I- Newton et le mouvement de la Lune (1642 - 1727)

En 1666, Newton étudie les caractéristiques du vecteur accélération d’un mobile animé d’un mouvement circulaire uniforme, puis les utilise pour le mouvement de la Lune, qui décrit une orbite circulaire de rayon r = 382800 km en 27 jours 7 heures 43 minutes et 11 secondes.

1)- Tester nos connaissances sur le mouvement circulaire uniforme. Étude préliminaire.

a)-  Représenter la trajectoire d’un mobile de centre d’inertie G animé d’un mouvement circulaire uniforme. Représenter le repère de FRENET.

-    Schéma de la représentation. Repère de Frenet.

 

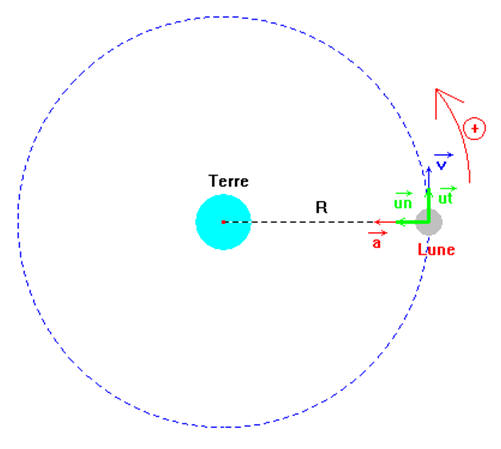
b)-  Donner les coordonnées du vecteur vitesse du point G, du mobile dans le repère de FRENET.

-    coordonnées du vecteur vitesse du point G, du mobile dans le repère de FRENET.

-     

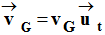
-    Avec :

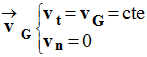
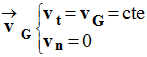
-    Avec l’orientation choisie.

-    Le vecteur vitesse est tangent à la trajectoire.

c)-  Donner les coordonnées du vecteur accélération dans le repère de FRENET.

-    coordonnées du vecteur accélération dans le repère de FRENET.

-     

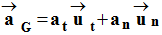
Avec 

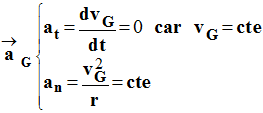
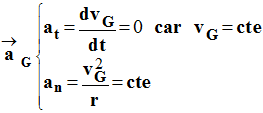
2)- Tester nos connaissances sur le mouvement circulaire uniforme. Répondre par Vrai ou Faux et justifier.

a)-  L’accélération est nulle car la vitesse est constante ?

-    Faux, l'accélération n'est pas nulle, elle est centripète car le mouvement est circulaire uniforme.

-     Le vecteur vitesse garde la même valeur, mais il change de direction à chaque instant.

-     

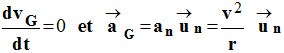
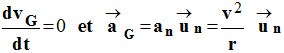
b)-  Le vecteur accélération est normal car la norme du vecteur vitesse ne change pas  ?

-    Faux, l'accélération est normale.

-     

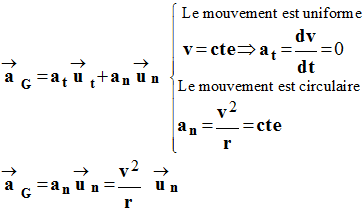
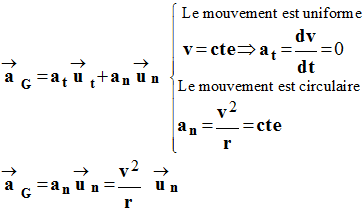
c)-  Le vecteur accélération est constant  ?

-    Faux si on parle du vecteur accélération :

-    Le vecteur accélération change de direction à chaque instant comme le vecteur vitesse

d)-  La valeur de l’accélération ne change pas ?

-    Vrai si on parle de la valeur.

-    La valeur de l'accélération ne change pas :

-     

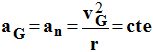
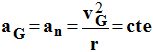
e)-  La norme du vecteur accélération ne change pas si la valeur de la vitesse est multipliée par deux ainsi que le rayon de l’orbite  ?

-    Faux,

-     

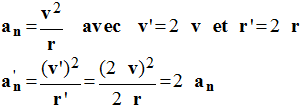
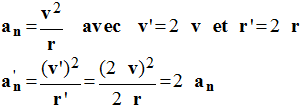
-    L'accélération est multipliée par deux.

3)- Calculer la valeur de la vitesse v de la Lune sur son orbite et en déduire la valeur de son accélération.

-    valeur de la vitesse v de la Lune sur son orbite.

-    Vitesse de la lune :

-     

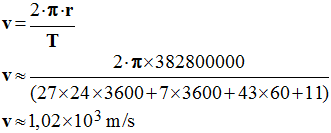
-     valeur de son accélération.

-     

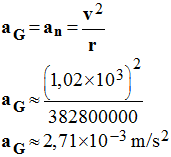
4)- En utilisant la deuxième loi de Newton, en déduire la valeur de l’intensité du champ de gravitation créé par la Terre au niveau de la Lune.

-    Valeur de l’intensité du champ de gravitation créé par la Terre au niveau de la Lune.

-    Valeur de l'intensité du champ de gravitation :

-    Il faut utiliser la deuxième loi de Newton : théorème du centre d'inertie.

-     

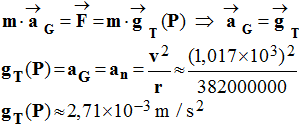
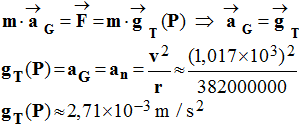
II- Le solénoïde.

Une bobine, assimilable à un solénoïde théorique, a une longueur ℓ = 50 cm et comporte N = 200 spires.

1)- Calculer la valeur du champ magnétique à l’intérieur de ce solénoïde lorsque l’intensité du courant qui le traverse vaut : I = 0,20 A (on donne μ₀ = 4 × π × 10 ^{– 7} S.I)

-    valeur du champ magnétique à l’intérieur de ce solénoïde.

-     

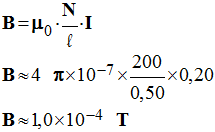
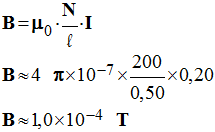
L’axe de la bobine est placé horizontalement et perpendiculairement au méridien magnétique.

Une petite aiguille aimantée est placée à l’intérieur de la bobine au voisinage de son centre.

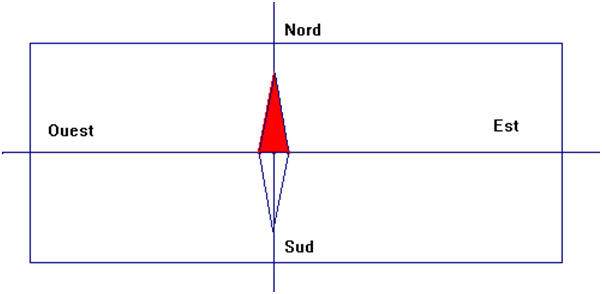
2)- Faire un dessin schématisant l’ensemble du système dans un plan horizontal, lorsqu’aucun courant ne circule dans la bobine.

On figurera les points cardinaux (Nord, Sud, Est et Ouest) et on indiquera les pôles de l’aiguille aimantée.

On peut représenter la bobine par un rectangle.

-    dessin schématisant l’ensemble du système dans un plan horizontal,

 

On fait passer un courant constant d’intensité I = 0,20 A dans la bobine.

L’aiguille aimantée dévie alors d’un angle α vers l’Est.

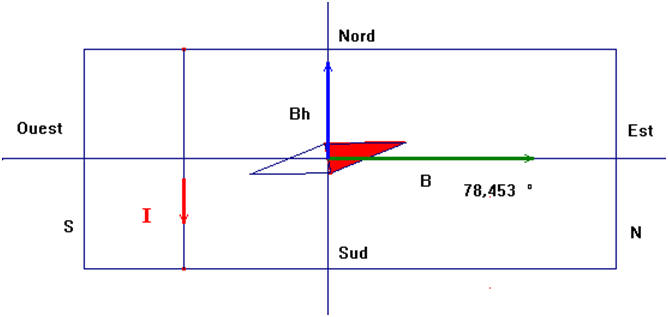
3)- Faire un schéma du dispositif à l’équilibre et indiquer : le sens du courant dans la bobine (il suffit de représenter une spire), les faces de la bobine.

 

-    schéma du dispositif à l’équilibre avec le sens du courant dans la bobine.

 

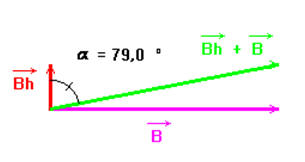
4)- Calculer la valeur de l’angle α (en degrés) dont l’aiguille a dévié (composante horizontale du champ magnétique : b_h = 2,0 × 10 ^{– 5} T.

-    valeur de l’angle α (en degrés) dont l’aiguille a dévié.

 

-     

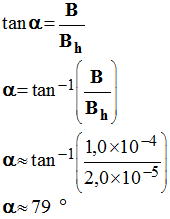
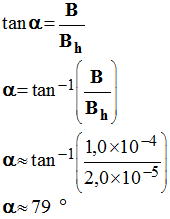
III- Dosage.

1)- On désire préparer par dilution un volume V = 100 mL d’une solution d’acide chlorhydrique de concentration C_A = 1,0 × 10 ^{– 2} mol / L en partant d’une solution mère de concentration C₀ = 2,5 × 10 ^–1 mol / L. Quel volume V₀ de solution mère doit-on utiliser et quel est le matériel nécessaire à la préparation de la solution  ? Justifier.

-    volume V₀ de solution mère nécessaire et matériel nécessaire à la préparation de la solution.

-    On utilise le fait qu’au cours de la dilution, il y a conservation de la quantité de matière du soluté.

 

-     

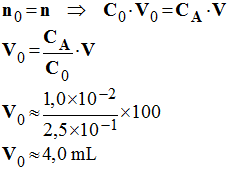
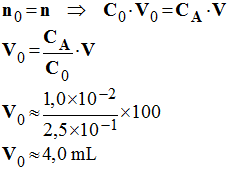
-    Matériel : pipette jaugée de 4 mL et fiole jaugée de 100 mL

2)- Afin de vérifier si la dilution est correcte, on effectue un dosage colorimétrique. On dose un volume V_A = 20 mL de la solution ainsi préparée par une solution d’hydroxyde de sodium (soude) de concentration C_B = 1,0 × 10 ^{– 2} mol / L et on constate qu’il faut verser un volume V_B = 24 mL de base pour atteindre l’équivalence acido-basique.

a)-  Définir l’équivalence acido-basique.

-    Définition de l’équivalence acido-basique.

-    Il y a équivalence lorsque les réactifs ont été mélangés dans les proportions définies par les coefficients de l’équation bilan.

-    À l’équivalence, d’après le bilan de matière, la quantité de matière d’ions hydronium initialement présente est égale à la quantité de matière d’ions hydroxyde ajoutée.

b)-  Écrire l’équation-bilan de la réaction de dosage. Quelles sont les caractéristiques de cette réaction  ?

-    L’équation-bilan de la réaction de dosage et caractéristiques de cette réaction.

-    La réaction fait intervenir un acide fort et une base forte :

H₃O ⁺   +   HO ^–   →   2 H₂O

-    La réaction est quasi totale, rapide, unique et exothermique.

c)-  Pour repérer l’équivalence, on utilise un indicateur coloré. Lequel ? pourquoi ? Justifier.

-    indicateur coloré.

-    La réaction fait intervenir un acide fort et une base forte.

-    À l’équivalence, le pH = 7.

-    On utilise le B.B.T comme indicateur coloré car la zone de virage (6,0 - 7,6) de cet indicateur contient le point d’équivalence E.

d)-  Calculer la concentration C_A de la solution d’acide chlorhydrique dosée.

-    Valeur de la concentration C_A de la solution d’acide chlorhydrique dosée.

-    À l’équivalence, d’après le bilan de matière, la quantité de matière d’ions hydronium initialement présente est égale à la quantité de matière d’ions hydroxyde ajoutée.

-     

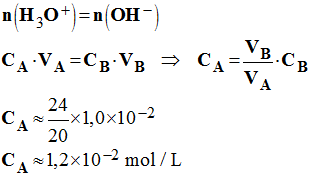
e)-  Quel volume de solution mère a-t-on en fait réellement utilisé si l’on suppose que les autres manipulations sont correctes ?

-    Volume de solution mère réellement utilisé si l’on suppose que les autres manipulations sont correctes.

-     

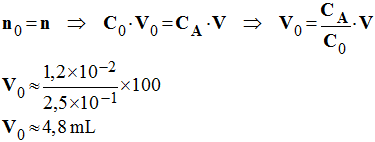
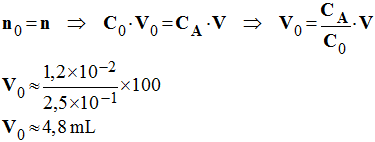
3)- Lors du dosage précédent, le pH est de 2,4 après un ajout de la solution d’hydroxyde de sodium de volume V’_B = 12,0 mL. Recenser toutes les espèces présentes dans la solution et calculer la concentration de tous les ions présents.

-    espèces présentes dans la solution et concentration de tous les ions présents.

-    Espèces présentes : H₃O⁺ ; HO^– ; Cl ^– ; Na⁺

-    Concentrations des différentes espèces présentes : 

-     

 

-     

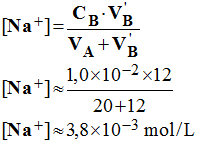
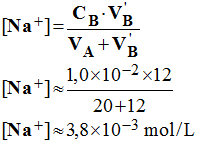
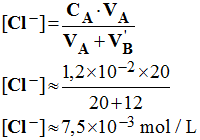
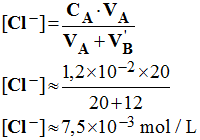
-    De la valeur du pH, on peut en déduire la valeur de la concentration en ion oxonium.

-    pH = 2,4

-    Par définition : [H₃O⁺] = 10 ^{– pH} mol / L

-    [H₃O⁺] ≈ 10 ^–2,4 mol / L

-    [H₃O⁺] ≈ 4,0 x 10 ^–3 mol / L

-    De la valeur du pKe, on peut en déduire la valeur de la concentration des ions hydroxyde.

-    [HO^–] = 10 ^{pH - pKe} mol / L

-    [HO^–] ≈ 10 ^{2,4- 14} mol / L

-    [HO^–] ≈ 2,5 × 10 ^–12 mol / L

-    Il y a un problème :

-    [Na ⁺] + [H₃O ⁺] ≈ 7,8 × 10 ^{– 3} mol / L

-    [HO ^–]  + [Cl ^–] ≈ 7,5 × 10 ^{– 3} mol / L

 

IV- Étude d'un acide.

Un acide AH, de concentration C = 1,0 × 10^–2 mol / L, a un pH égal à 3,4.

1)- Calculer la concentration des différentes espèces présentes dans l'eau.

-    concentration des différentes espèces présentes dans l'eau.

-    Espèces présentes : H₃O ⁺ ; HO ^– ; A ^– ; AH

-    pH = 3,4

-    Par définition : [H₃O ⁺] = 10 ^{– pH} mol / L

-    [H₃O ⁺] ≈ 10 ^{– 3,4} mol / L

-    [H₃O ⁺] ≈ 4,0 × 10 ^–4 mol / L

-    [HO ^–] = 10 ^{pH – pKe} mol / L

-    [HO ^–] ≈ 10 ^{3,4 – 14} mol / L

-    [HO ^–] ≈ 2,5 × 10 ^–11 mol / L

-    électroneutralité :

-     [H₃O ⁺] = [HO ^–]  + [A ^–]

-    Or  [HO ^–]  << [H₃O ⁺]

-    [H₃O ⁺] ≈ [A ^–] ≈ 4,0 × 10 ^{– 4} mol / L

-    Conservation de la matière :

-    [AH]  + [A ^–] = C

-    [AH]  =  C – [A^–]

-    [AH]  ≈ 1,0 x 10 ^{– 2} – 4,0 × 10 ^{– 4}

-    [AH]  ≈ 9,6 × 10 ^{– 3} mol / L

2)- Calculer le coefficient d'ionisation α de cet acide.

-    Coefficient d'ionisation α de cet acide.

-    On peut négliger la réaction d’autoprotolyse de l’eau.

 

-    Quantité de matière d’acide ionisé :  x_f = [A^–] . V

-    Quantité de matière initiale d’acide : n = n (AH)_i =  x_max = C . V

-    Coefficient d’ionisation :

-     

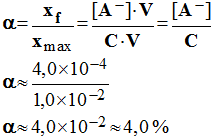
3)- Comment peut-on qualifier cet acide ? Écrire l'équation bilan de la réaction entre l'acide et l'eau.

On donne : pK_e = 14 ; .

 

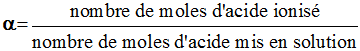-    équation bilan de la réaction entre l'acide et l'eau et qualificatif

-    Acide faible : la réaction avec l’eau est limitée et pH > – log C