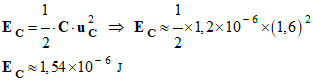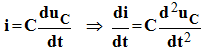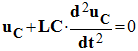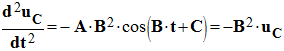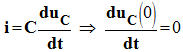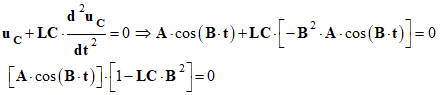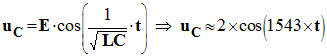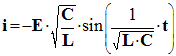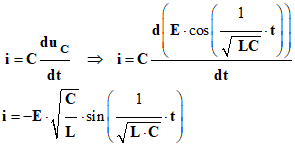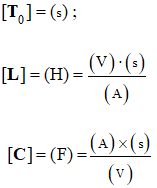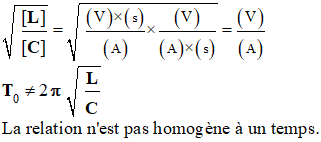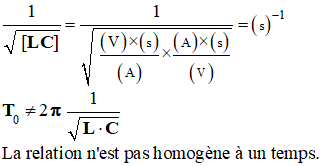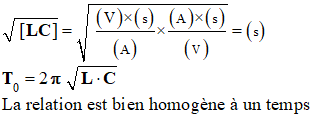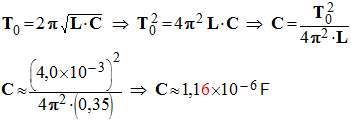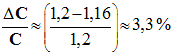II- Exercice 2 : Mesure de la capacité d’un condensateur

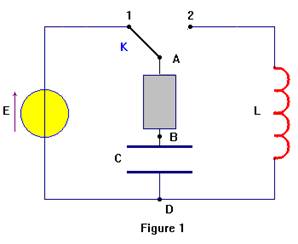
On considère le montage de la figure 1 composé :

-  d’un générateur de tension de force électromotrice E.

-  d’un condensateur de capacité C inconnue.

-  d’un conducteur ohmique de résistance R = 20 Ω.

-  d’une bobine d’inductance L = 0,35 H.

-  d’un interrupteur à deux positions.

-  d’un oscilloscope.

1)- Partie A :                   Circuit R, C

Le condensateur est initialement déchargé, à la date t = 0, on ferme l’interrupteur en position 1.

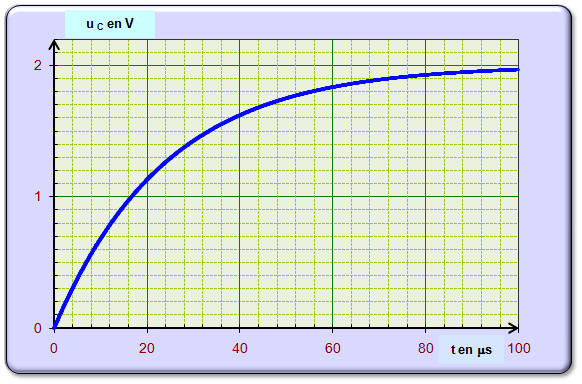
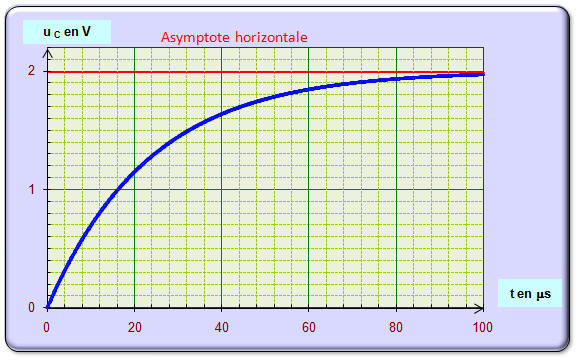
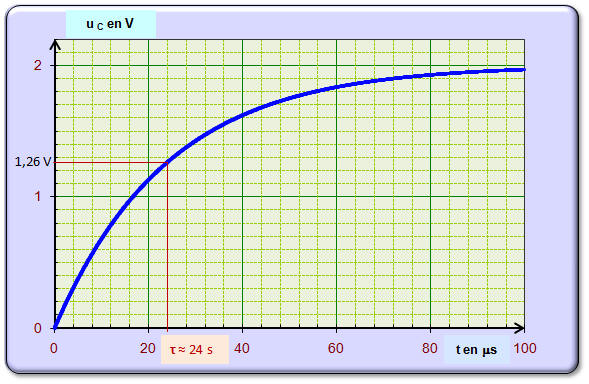
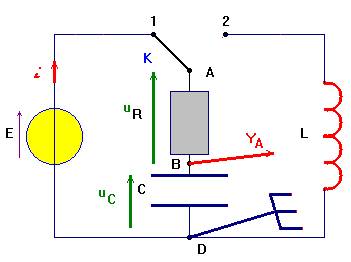
On enregistre la tension u_C ; On obtient la courbe de la figure 2.

a)- Représenter (sur le schéma de la figure 1 de la feuille en annexe) par une flèche le sens de circulation du courant d’intensité i

dans le circuit ainsi que les tensions u_C et u_R aux bornes du condensateur et du conducteur ohmique afin de travailler en convention récepteur.

Figure 1 :

b)- Indiquer  sur le schéma de la  figure 1 (de la feuille en annexe) les connexions à réaliser pour visualiser la tension u_C avec un oscilloscope.

c)- Quelle tension permet de connaître les variations de l’intensité du courant i en fonction du temps ? Justifier votre réponse ?

-  La tension u_R permet d’après la loi d’Ohm de connaître les variations de l’intensité i en fonction du temps :

-  u_R = R i

-  Il y a proportionnalité entre u_R et i.

d)- Déterminer la tension E aux bornes du générateur ainsi que les valeurs de l’intensité du courant au début et à la fin de la charge.

-  Valeur de la tension u_C aux bornes du condensateur lorsque le régime permanent est atteint :

-  La loi d’additivité des tensions permet d’écrire la relation suivante : E = u_R  + u _C

-  Lorsque le condensateur est chargé, l’intensité du courant dans le circuit est égale à zéro :

-  u_R  = 0   ⇒  E = u_C = 2,0 V :

-  Valeur que l’on détermine grâce à la représentation graphique de u_C.

-  Valeurs de l’intensité du courant :

-  Au début de la charge, la tension aux bornes du condensateur est nulle (il est déchargé) :

-  

-  Lorsque le condensateur est chargé, l’intensité du courant s’annule dans le circuit : i_∞ = 0,0 A.

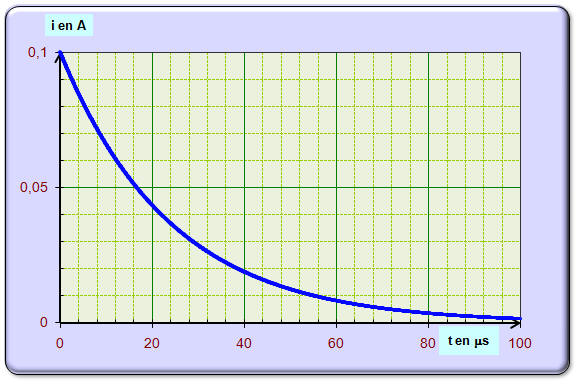
e)- Tracer l’allure de la courbe donnant l’évolution de l’intensité i du courant au cours du temps.

-  Allure de la courbe :

f)-  On rappelle que la tension u_C atteint 63 % de sa valeur maximale au bout d’une durée τ appelée constante de temps du circuit.

En déduire la valeur de τ puis la valeur de la capacité C du condensateur.

-  Au bout de la durée τ,

-  

-  Graphiquement, on trouve : τ ≈ 24 s.

-  Valeur de la capacité C du condensateur :

-   

2)- Partie B :                   Circuit R, L, C

Le condensateur étant chargé, l’interrupteur est basculé en position 2. On enregistre la tension u_C.

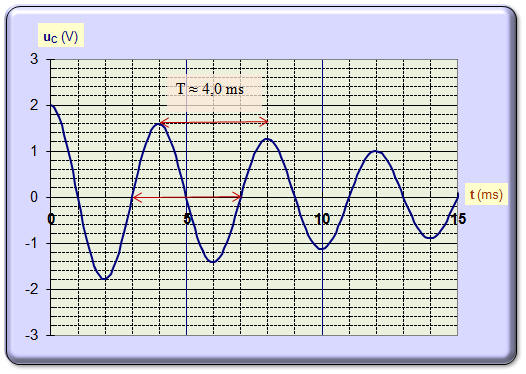
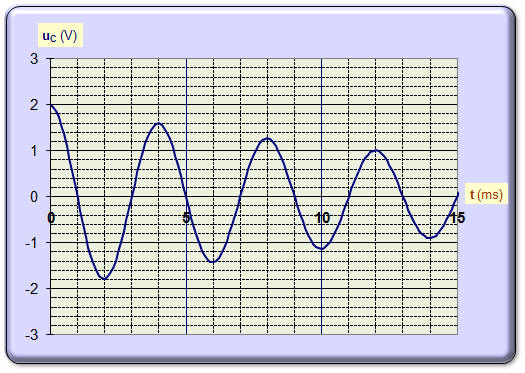
On obtient la courbe de la figure 3 de la feuille en annexe.

a)- Comment appelle-t-on le type d’oscillations observées ?

-  On observe des oscillations libres amorties.

b)- Mesurer la pseudo-période T des oscillations.

-  pseudo-période T des oscillations : graphiquement : T ≈ 4,0 ms.

c)- Calculer l’énergie E_C emmagasinée dans le condensateur à la date t ₁ = 4,0 ms.

Quelle est à cet instant l’énergie E_L emmagasinée dans la bobine ainsi que l’énergie totale E_T du circuit ?

Cette dernière reste-t-elle constante ? Pourquoi ?

-  Au temps t = 4,0 ms, la tension u _C aux bornes du condensateur est maximale : u_C ≈ 1,6 V.

-  Valeur de l’énergie emmagasinée dans le condensateur :

-  Énergie totale dans le circuit au temps t = 4,0 ms :

-  Comme la tension u _C aux bornes du condensateur est maximale , E_L = 0,0 J

-  E_T = E_C  +  E_L = E _C ≈ 1,54 × 10 ^{– 6} J

-  L’énergie totale dans le circuit diminue au cours du temps à cause de la dissipation d’énergie par effet Joule dans les résistances du circuit.

 On supprime à présent du circuit le conducteur ohmique.

d)- Établir l’équation différentielle vérifiée par la tension u_C.

-  La loi d’additivité des tensions dans le circuit permet d’obtenir la relation suivante :

-  u_C  +  u_L = 0 (1)

-  Or 

-  On tire :

-  On en déduit l’équation différentielle linéaire du deuxième ordre sans second membre :

-   (2)

e)-   La solution de cette équation différentielle est de

la forme u_C = A cos (B.t + C ), déterminer les valeurs des

constantes A , B et C .

-  détermination des constantes :

-  On calcule les dérivées successives :

-   et

- 

-  Conditions initiales : au temps t = 0 s, i = 0 A et u_C = E = 2 V.

-  Au temps t = 0 s, i = 0 A , comme :

-  –  A.B sin (C) = 0 ⇒  sin (C) = 0  ⇒  C = 0 ou C = π

-  Au temps t = 0 s, u_C (0) = E = 2 V, comme :

-  u_C (0) = A sin (C) = E > 0 ⇒  C = 0 et A = E

-  L’expression u_C = A cos ( B.t + C ) vérifie l’équation différentielle (2), en conséquence :

-  Cette équation doit être vérifiée ceci quel que soit t : il faut que :

-   

-  Expression de la solution :

-  

f)-  Déduire de la question précédente que l’intensité du courant électrique dans le circuit peut s’écrire :

-  Intensité du courant électrique dans le circuit :

g)-   La période propre du circuit L, C est donnée par une des relations suivantes :

A l’aide d’une étude dimensionnelle choisir la bonne relation.

-  Analyse dimensionnelle :

h)-  En admettant que la pseudo-période T est identique à la période T₀ (mesurée à la question b)- ) ,

en déduire la valeur de la capacité C du condensateur .

Comparer cette valeur  à celle trouvée à la question f)- de la partie A.

-  Valeur de la capacité du condensateur :

-  

-  En toute logique, on doit garder 2 chiffres significatifs.

-  écart relatif :

-  L’écart relatif entre les deux valeurs est faible.

-  Les deux valeurs sont cohérentes.