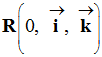I- Exercice 1 :    Saut à skis idéal (4 pts)

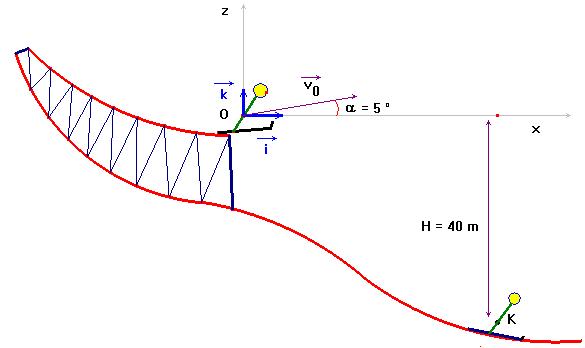
À la date t = 0 s, un skieur émerge d’un tremplin à la vitesse  de valeur 92 km / h, inclinée d’un angle  α = 5 ° sur l’horizontale.

On considère le mouvement du centre d’inertie G du skieur en ne prenant pas en compte les actions de l’air sur le système.

1)- Le skieur est-il en chute libre lorsqu’il a franchi le tremplin ? Pourquoi ?

2)- établir les expressions littérales des équations horaires du mouvement de G dans le repère .

3)- En déduire l’équation de la trajectoire.

4)- Soit K la position de G au moment où le skieur retombe sur la piste. La dénivellation entre O et K est de 40 m.

a)- Calculer la durée t_K du saut.

b)- En déduire la valeur de la coordonnée x_K du point K.

c)- Calculer la valeur de la vitesse de G à l’instant où il arrive en K et l’angle de ce vecteur avec l’horizontale.

5)- En compétition, les valeurs de x_K sont supérieurs à 100 m Pourquoi ?

Données : valeur du champ de pesanteur : g = 9,8 m / s².