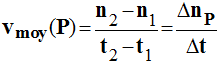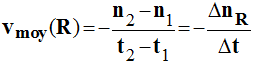|
Chim N° 05 :
|
|
|
|
I- Classification cinétique des réactions naturelles.
- Une réaction est rapide si sa durée est très inférieure à la seconde.
- Exemples : les réactions de précipitations sont généralement rapides, de même des réactions acido-basiques sont des réactions rapides.
Ag
+ (aq)
+ Cl
– (aq)
→ AgCl
(s)
- Le précipité blanc apparaît immédiatement : la réaction est instantanée.
- Une réaction est lente si sa durée est de l'ordre de quelques secondes à plusieurs minutes.
- On peut observer l'évolution de la réaction.
- Exemples : réaction entre l'eau oxygénée et les ions iodure.
- Expérience : cette expérience sera étudiée lors d'une séance de travaux pratique. La réaction est lente à température ambiante.
- Le milieu réactionnel se teinte en jaune brun au cours du temps.
3)- Réaction infiniment lente.
- Une réaction est infiniment lente si sa durée est de l'ordre de plusieurs jours à plusieurs semaines.
- Exemple : solution aqueuse de permanganate de potassium pour un peu réviser.
- Étude de la réaction :
|
Mn O4 –
(aq) / Mn O2
(aq) |
E01 = 1,69 V |
|
O2 (aq) / H2
O (l) |
E02 = 1,23 V |
- écrire les demi-équations électroniques et écrire l'équation bilan de la réaction naturelle.
- On utilise la méthode suivante :
- On équilibre l'oxygène avec de l'eau, l'hydrogène avec H+ et les charges avec les électrons.
|
(MnO4
– (aq)
+ 4
H
+(aq)
+ 3
e
–
=
MnO2 (aq)
+ 2 H2O
(l)
) x
4 |
|
(H2O (ℓ)
= O2
(aq) +
4 H
+(aq)
+ 4 e
–
)
x
3 |
|
MnO4
– (aq)
+ 2 H2O
(ℓ)
→ 4 MnO2 (aq)
+ 3 O2 (aq)
+
4 HO
– (aq) |
- L'apparente stabilité de la solution provient de la grande lenteur de la réaction naturelle.
II- Étude expérimentale de la cinétique d'une réaction chimique. (TP chimie N° 7).
1)- Les techniques du suivi de l'évolution de la réaction.
a)- Introduction :
- Le suivi de la réaction peut se faire de deux façons :
- Par dosage (dosage acido-basique ou dosage d'oxydoréduction).
- Par spectrophotométrie.
b)- Le dosage :
- il faut arrêter la réaction à un instant quelconque t.
- Pour ce faire, on réalise la trempe du mélange réactionnel, c'est-à-dire que l'on refroidit brutalement le mélange réactionnel pour bloquer la réaction.
- On réalise le dosage d'un des réactifs ou d'un des produits à l'aide d'une solution titrée.
- Ainsi, on peut connaître la quantité de matière d'un des réactifs ou d'un des produits à un instant donné.
c)- La spectrophotométrie :
-
On utilise cette méthode en cinétique
chaque fois qu'un réactif ou un produit absorbe sélectivement la lumière.
-
Lorsqu'il se forme du diiode au cours de
la réaction entre les ions iodure et l'eau oxygénée, le mélange
réactionnel change de couleur au cours du temps.
-
On peut suivre l'avancement de la
réaction grâce à la variation
absorbance du mélange réactionnel et à la loi de
BEER-LAMBERT :
- Pour une lumière monochromatique de longueur d'onde λ qui traverse une substance S sur une longueur L, on utilise la relation suivante :
|
A = ε . L . [S] |
A : absorbance |
|
ε : coefficient
d'extinction en
mol
–1.L.cm
–1 |
|
|
L : longueur de
la cuve en cm |
|
|
[S]
concentration
en mol / L |
- Exemple : Dans le cas du diiode :
- λ = 410 nm
-
ε =
1,8 x 104 mol
–1.L.
cm –1.
- Remarque : ε dépend de la longueur d'onde et de la température et de la substance).
- On peut écrire :
-
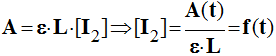
- L'absorbance est proportionnelle à la concentration.
III- Vitesse d'évolution d'une espèce chimique.
- Considérons la réaction naturelle suivante :
α . A
+
β . B
→ γ . C
+ δ . D
- A et B sont les réactifs, C et D sont les produits et α, β, γ et δ sont les coefficients stœchiométriques.
- Pour connaître l'évolution d'une réaction chimique, il suffit de connaître à chaque instant la quantité de matière présente de l'une des espèces chimiques.
- Exemple : considérons la réaction chimique suivante.
- Au temps t = 0 s, on mélange 100 mL d'une solution de peroxodisulfate de potassium de concentration C1 = 0,05 mol / L et 100 mL d'une solution d'iodure de potassium de concentration C2 = 0,5 mol / L.
- Il se produit la réaction suivante :
|
(S2O82
–
(aq)
+ 2 I–
(aq)
→ 2 SO42
–
(aq)
+ I2 (aq) |
|
Équation |
S2O82
–
(aq) |
+ 2 I –
(aq) |
→ |
2
SO4
2 -
(aq) |
+
I2 (aq) |
|
|
État du système |
Avancement |
|||||
|
État initial
(mol) |
x = 0 |
n1 |
n2 |
0,0 |
0 ,0 |
|
|
Au cours de la transformation |
x |
n1
– x |
n2
– 2 x |
2 x |
x |
|
|
État final
(mol) |
x = xmax |
n1
– x max |
n2
– 2 xmax |
2 xmax |
xmax |
|
- x est lié à « l’avancement de la réaction » : x ≤ n1 et 2 x ≤ n2
- Si par dosage, on détermine la concentration en diiode au temps t, on peut en déduire la quantité de matière x en diiode,
- puis les quantités de matière des espèces présentes dans le milieu réactionnel.
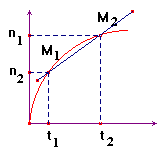
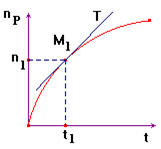
2)- Vitesse moyenne de formation d'un produit P.
|
- On suit l'évolution de la quantité de matière d'un produit au cours du temps : - np =
f (t). - Par définition, la
vitesse moyenne de formation du produit P : -
- Cette vitesse est
un nombre positif et l'unité S.I : mol / s. - Elle est numériquement égale au coefficient directeur de la droite passant par les points M1
et M2 d'abscisses t1 et
t2.
|
|
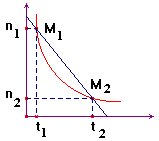
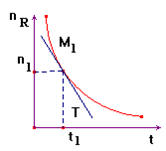
3)- Vitesse moyenne de disparition d'un réactif R.
|
- On suit l'évolution
de la quantité de matière d'un réactif au cours du temps : - nR
= g (t). - Par définition, la
vitesse moyenne de disparition du réactif R : -
- Cette vitesse est
un nombre positif et l'unité S.I : mol / s. - Elle est
numériquement égale à l'opposé du coefficient directeur de la droite passant par les
points M1 et M2
d'abscisses t1 et t2. |
|
4)- Vitesse instantanée de formation d'un produit P.
|
- La vitesse instantanée v1(P) de formation du produit P à la date t1 est, par définition, la limite de la vitesse moyenne de formation de ce même produit
entre t1 et t2 quand
t2 tend vers t1. -
On écrit : - Cette limite est égale à la valeur prise par la dérivée de la fonction np = f
(t) au temps t1. -
On écrit : - Graphiquement : cette vitesse est numériquement égale à la valeur du coefficient directeur de la tangente T à la courbe np = f (t) au point
M1 d'abscisse t1. |
|
5)- Vitesse instantanée de disparition d'un réactif R.
|
-
La vitesse instantanée v1(R) de
disparition du réactif R à la date
t1 est, par définition, la limite de la
vitesse moyenne de
disparition de ce même réactif entre t1 et
t2 quand
t2 tend vers t1. -
On écrit : -
Cette limite est égale à l'opposée de la valeur prise par la dérivée
de la fonction nR = g(t) au temps
t1. -
On écrit : -
Graphiquement : cette vitesse est numériquement égale à l'opposée
de la valeur du coefficient directeur de la tangente T
à la courbe
nR = g(t) au point M1
d'abscisse t1. |
|
6)- Relation entre les vitesses.
- Équation bilan générale :
α . A
+
β . B
→ γ . C
+ δ . D
-
D'après le bilan molaire de la réaction :
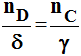
- δ et g sont des constantes indépendantes du temps.
-
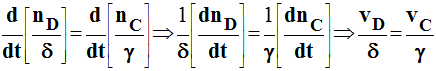
- On peut généraliser : ceci est valable aussi pour les réactifs :
-
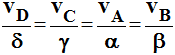
- Étude d'un exemple :
-
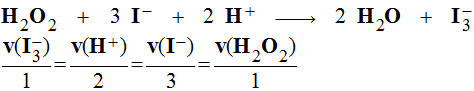
7)- Cas particulier important. Vitesse volumique.
- Si le mélange réactionnel a un volume constant V au cours de la réaction, on peut dans ce cas suivre l'évolution de la réaction en travaillant avec les concentrations :
- nA = [A] . V avec V =cte.
-
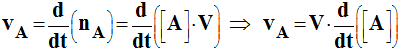
- On parle alors de vitesse volumique de formation pour un produit et de disparition pour un réactif.
- On écrit :
- Vitesse moyenne :
-
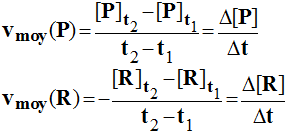
- Vitesse instantanée :
-
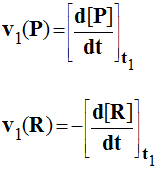
-
Unités : dans le S.I : mol.
L–1.
S –1
-
on utilise souvent : mol.
L–1.min
–1
|
-
Le temps de demi-réaction noté t ½ est défini par rapport à l'un des
réactifs, en général celui qui est introduit par défaut. -
à la date t
= 0, la concentration initiale du réactif A est [A0].
- Le temps de demi-réaction t ½ est la date pour laquelle :
-
Détermination graphique : -
Remarque :
-
t ½ dépend en général de la concentration initiale du
réactif A. -
Le temps de demi-réaction n'est pas caractéristique de la substance
A. -
Le temps de demi-réaction permet d’évaluer la durée
nécessaire à l’achèvement de la transformation chimique
étudiée. |
|
IV-
Applications : ex 5 page 33 ; ex 6
page33 ; ex 15 page 35.



|
|
|
|